深海系泊浮體物面非線性時域耦合動力分析

韓旭亮，段文洋，馬 山，謝 彬

（1.中海油研究總院，北京 100028；2.哈爾濱工程大學 船舶工程學院，哈爾濱 150001）

深海系泊浮體物面非線性時域耦合動力分析

韓旭亮1，2，段文洋2，馬 山2，謝 彬1

（1.中海油研究總院，北京 100028；2.哈爾濱工程大學 船舶工程學院，哈爾濱 150001）

文章基于三維時域勢流理論和彈性細長桿理論，研究并提出了深海系泊浮體物面非線性時域耦合動力分析方法。該方法采用時域物面非線性理論方法在瞬態位置直接時域模擬系泊浮體所需水動力，結合有限元方法計算系泊纜索的動力響應，利用異步耦合方法實現浮體和系泊纜索的時域耦合動力求解。既滿足系泊浮體時域水動力耦合，又滿足系泊浮體和系泊纜索動力耦合。通過對二階非線性不規則波作用下深海系泊半潛式平臺的時域耦合響應特性進行研究，將不同海況下物面非線性時域耦合靜力響應和動力響應與間接時域耦合動力響應的三種方法計算結果進行比較。研究結果表明，系泊纜索動力響應明顯，平臺瞬態空間位置對垂蕩低頻運動影響較大，有必要在平臺瞬時濕表面采用動力響應方法進行深海系泊浮體時域耦合響應分析。

時域格林函數；物面非線性；時域耦合；動力響應；細長桿理論

0 引 言

海底石油和天然氣的開采與勘探作業都離不開深海浮式結構物的支撐，它在深海油氣開發中發揮著重要的作用。目前海洋工程中典型的深海系泊浮體主要有：Spar平臺、半潛式海洋平臺、TLP平臺和FPSO等。深海系泊浮體通過動力定位或者系泊纜索相對定位于作業海域，海面復雜的風浪流載荷使其產生波頻運動和低頻運動。大幅低頻運動會在細長柔性桿件的系泊纜索中誘發很大張力，從而作用在系泊浮體上限制其運動。隨著平臺工作水深的增加，系泊纜索的非線性動力響應逐漸增強。因此，為了準確預報深海系泊浮體耦合運動及外載荷，有必要采用動力學耦合方法來分析平臺和系泊纜索的相互作用。然而系泊系統耦合分析并不是一個新概念，只是由于不同時期計算方法和能力的限制，沒有實現完全耦合的高度。近年來，隨著國內外海洋油氣資源的加速發展和對深海系泊浮式結構物的迫切需求，國內外許多學者進行了許多有意義的研究，并取得了很大的進步。表1選取部分研究工作給出了系泊浮體耦合運動的研究進展。

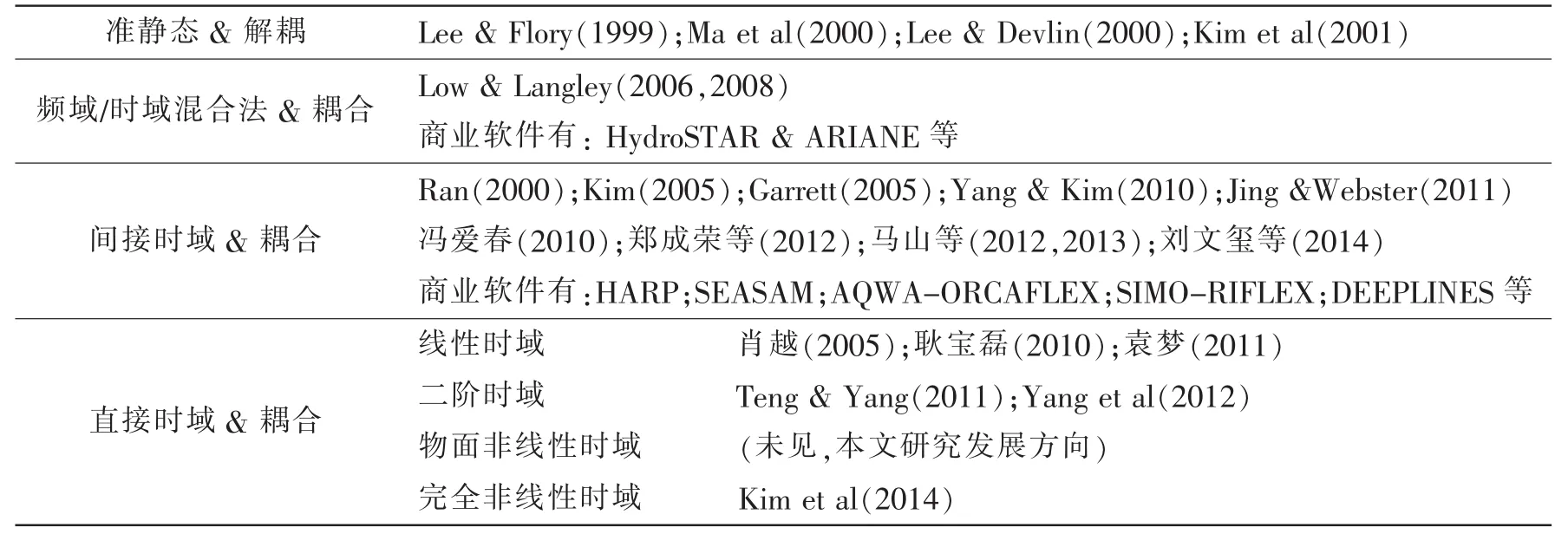
表1 系泊浮體耦合運動研究進展Tab.1 Research progress of the coupled motion of amooring platform

系泊浮體耦合運動首先為基于懸鏈線理論或者頻域計算的準靜態解耦分析方法。然而有研究[1-5]指出該方法已不適用深海系泊浮體耦合計算分析，可靠性和準確性都不能達到工程需求。隨著平臺工作水深的增加，系泊纜索的非線性動力響應和阻尼逐漸增強，必須考慮平臺與系泊系統的耦合動力計算。其次為頻域/時域混合耦合方法[6-7]，它在頻域中計算波頻運動，而低頻運動在時域中計算。結果發現該方法在適用范圍內與時域耦合方法計算精度相當，而計算時間僅為時域耦合方法的10%左右。商業軟件HydroSTAR&ARIANE用于設計平臺系泊系統。然而，國際和國內目前普遍采用頻域轉時域的間接時域方法[8-17]進行系泊浮體時域耦合運動分析，即在頻域中計算浮體本身水動力系數、浮體穩態水動力以及平均漂移力，通過傅里葉變換將頻域水動力系數轉為時域脈沖響應函數，采用集中質量方法[18]或者細長桿有限元方法[19-20]對系泊纜索響應分析，進而實現系泊浮體間接時域耦合運動模擬。同時國外也開發了可以用于實際海洋工程的數值計算程序和相關商業軟件，常用的主要有HARP、SEASAM、AQWA-ORCAFLEX、SIMO-RIFLEX和DEEPLINES等。但是這并不是真正的時域，系泊浮體時域耦合分析所需的水動力應該在時域中直接表述。直接時域耦合分析系泊浮體的研究還處于研究發展階段，有學者[21-23]采用直接時域方法對系泊浮體進行了時域耦合研究，但僅考慮到線性時域的階段。盡管有學者[24-25]通過攝動展開邊界面建立了二階時域理論模型，能夠考慮部分非線性因素得到時域解，但其前提假設仍為物體在平均濕表面位置做微幅運動，并不是物體真實準確的濕表面位置，忽略了浮體低頻漂移和轉動造成位置變化對水動力及系統動力響應的影響。最好采用完全非線性方法[26]來分析系泊浮體全耦合運動響應，但是該方法通常需要超級計算機來滿足計算量和存儲量需求，而且在處理復雜結構物和強非線性等問題時，會給實際數值計算帶來很多挑戰和困難。

本文基于三維時域勢流理論和彈性細長桿理論，研究并提出了深海系泊浮體物面非線性時域耦合動力分析方法，建立了深海系泊浮體物面非線性時域耦合數學模型。采用時域格林函數方法在深海浮式結構物及其系泊系統的瞬態位置直接時域模擬系泊浮體所需水動力，采用有限元方法計算系泊纜索的動力響應，利用異步耦合方法在各自最佳的時間間隔求解系泊浮體時域運動方程和系泊纜索動力方程，通過在導纜孔處傳遞浮體運動響應和系泊纜索張力信息，實現了兩者時域動力耦合求解。最后計算分析了二階非線性不規則入射波浪作用下深海系泊半潛式平臺的時域耦合動力響應性能。

1 時域耦合分析理論模型

1.1 坐標系的建立

圖1為系泊浮體與波浪相互作用的示意圖。大地坐標系為O-XYZ，原點O位于靜水面；XOY平面與靜水面一致，OZ軸垂直向上；浮體重心坐標系為G-X′Y′Z′與浮體固定在一起，隨浮體作搖蕩運動；另一個坐標系為O′-X′Y′Z′不隨浮體搖蕩，始終位于平衡位置，初始時刻原點O′與重心G重合。圖中Ai為系泊纜索的錨泊點，Pi0為初始t0時刻導纜孔初始位置，Pi為某t1時刻導纜孔瞬時位置，Li0為初始t0時刻系泊纜索初始長度，Li為某t1時刻系泊纜索長度。系泊纜索編號i=1，…，NM，且NM為系泊纜索數目。h為水深。

圖 1系泊浮體與波浪相互作用示意圖Fig.1 The sketch ofwave interaction with amooring offshore structure

1.1 浮體時域運動方程

假設浮式結構物為剛體，利用動量定理計算浮體重心處任意六自由度的運動響應，記為ηj（j=1，2，…，6），分別表示縱蕩、橫蕩、垂蕩、橫搖、縱搖和艏搖運動，故波浪中浮體時域運動方程可以寫為：

式中：［m］和［I］分別為質量矩陣和慣性力（矩）矩陣。X（t）和V（t）分別為浮體重心的平動位移和速度，θ（t）和ω（t）分別為轉動歐拉角和角速度。［B ］為隨時間變化的歐拉角和角速度之間轉換矩陣[27]，可以表示為

式中：下角標H表示流體動力載荷項，下角標C表示流體靜力載荷項，下角標M表示系泊載荷項。

1.3 邊界條件和時域積分方程

假設流體是不可壓縮，無旋和無粘的理想流體，水深h為無限水深。流場Ω中的速度勢可以表示為:

式中：Φ為擾動速度勢，p（x，y， ）z 為場點。無限水深下不規則入射波浪的一階和二階速度勢[28]可以寫為：

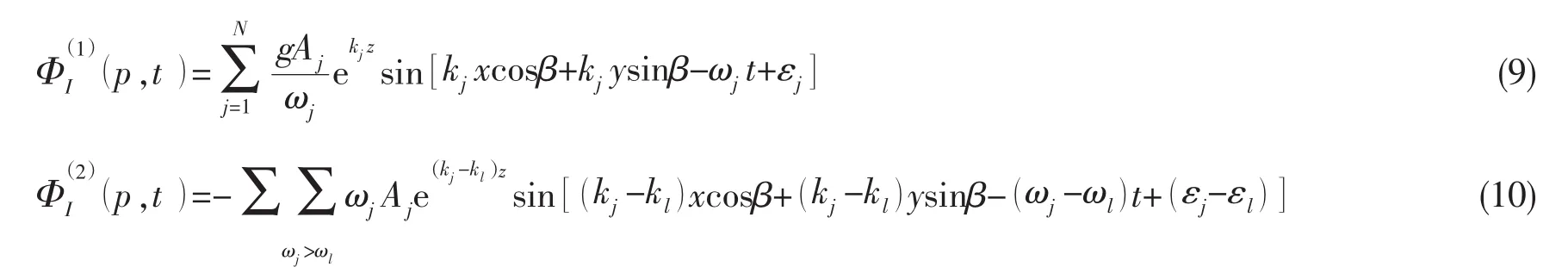
式中：Aj，ωj，kj和εj分別表示不規則波中第j個規則波的波幅、圓頻率、波數和隨機相位角。色散關系為kj=ωg。下角標j和l表示的含義相同。g為重力加速度，β為浪向角。上式滿足的自由面條件可以寫為

式中：f1和f2分別為

式中：Ψj=kjx cosβ+kjy sinβ-ωjt+εj。

由圖1可以看出，流場Ω由物體濕表面SB（）t，自由面SF，無窮遠底面SD和無窮遠處控制面S∞組成。擾動速度勢Φ滿足的定解問題為：

式中：物面SB的單位法向量n指向流域外部，物體沿法線方向速度為Vn。擾動速度勢仍在線性自由面下求解，但是物面邊界條件中不僅包括瞬態位置的影響，還包括二階非線性入射速度勢的影響。

大地坐標下，滿足線性自由面條件的無限水深時域格林函數[29]包括瞬時效應項G0和記憶效應項兩部分，它可以表示為：

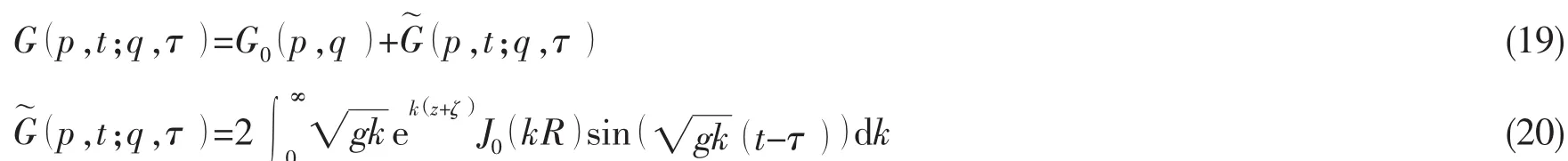
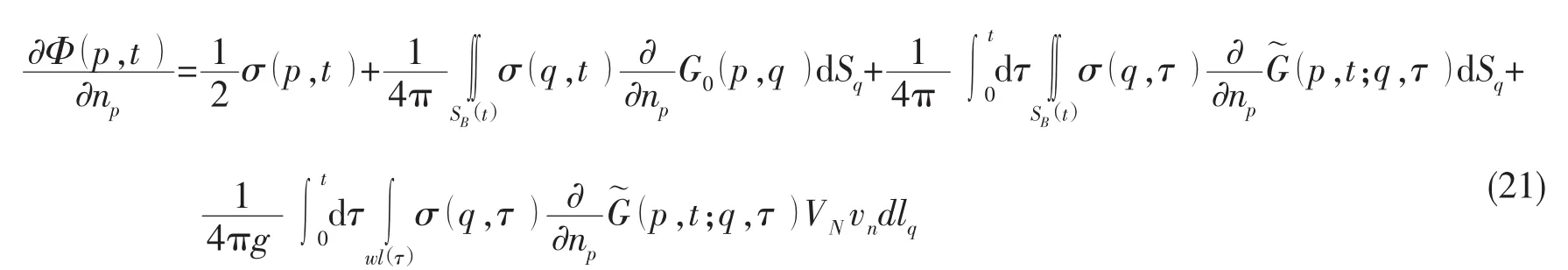
式中：σ（q，τ ）為源強，VN表示水線wl（τ）在其平面法線方向N上的運動速度，且vn=（N·n ）VN。

1.4 時域非線性水動力計算方法

通常根據Bernoulli公式計算浮體物面壓強，然后在浮體濕表面上進行壓力積分，得到浮體的時域水動力。但是，浮體物面非線性時域水動力計算中需要每時刻重新劃分捕捉物體空間幾何位置，相鄰時間間隔控制點的位置不同。這樣就導致Bernoulli公式中第一項速度勢關于時間的偏導數?Φ/?t的計算不準確不方便。本文采用先積分后微分[30]的方法，計算系泊浮體時域非線性水動力的公式可以寫為

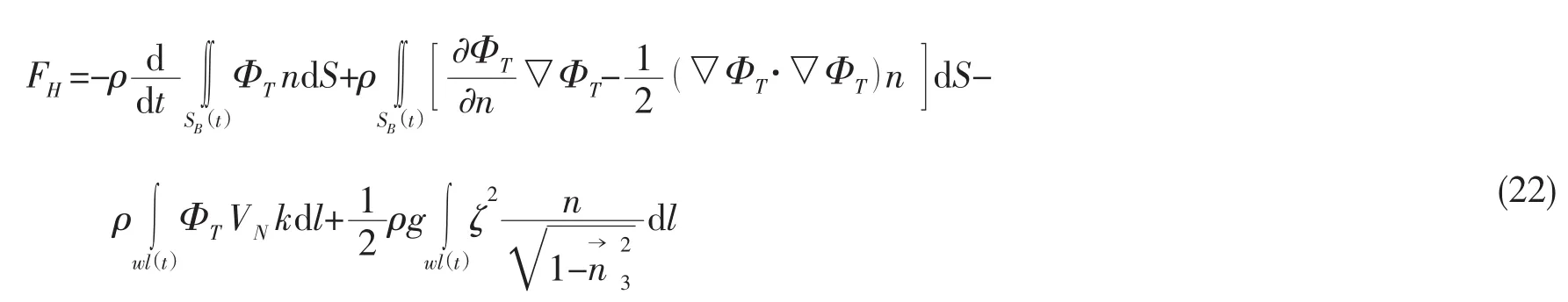
式中：前四項為瞬時平均濕表面貢獻，最后一項為水線附近興波貢獻。采用這種方法不需要每時刻逐點對時間微分，既有效提高了計算精度和效率，又普遍適用于數值計算。作用在浮體上的靜力載荷可以寫為

1.5 系泊纜索響應計算方法

非線性水動力作用下深海系泊浮體會偏離其平衡位置發生大幅低頻漂移運動。本文基于三維彈性細長桿理論[14]，建立了系泊纜索動力分析有限元數值模型，將桿件的控制方程離散為含有節點未知變量的代數方程組，利用牛頓迭代方法求解靜力問題，利用Adam-Moulton顯式單步積分方法求解動力問題[31]。系泊纜索頂端通常采用鉸接方式連接系泊浮體的導纜孔位置，其頂端與導纜孔處位移速度一致，在導纜孔處互相傳遞系泊浮體運動響應和系泊纜索張力響應信息，實現兩者的時域動力耦合求解。限于篇幅原因，這里不再詳述。

2 數值計算實施途徑

波浪中系泊浮體時域運動方程是非線性方程組，其數值計算過程是一個復雜的問題。不僅是因為每時刻浮體瞬時位置改變，而且所有涉及用于計算浮體任意六自由度運動響應量都依賴于時間變化，浮體位置、速度和加速度在求解運動方程前都是未知的。圖2給出系泊浮體物面非線性時域耦合計算的流程圖。波浪中系泊浮體時域耦合運動方程的求解步驟主要包括：

（1）給定浮體初始狀態及外界環境工況參數，對系泊系統進行初始靜平衡分析；

（2）確定浮體瞬時空間位置以及系泊纜索頂端導纜孔瞬時空間位置；

（3）建立滿足初邊值條件的時域積分方程，計算浮體受到的水動力FH（t）和恢復力FC（t）；

（4）求解時域耦合運動響應方程Ma=F（t）得到時刻t浮體的位移和速度；

（5）將浮體響應在時間間隔△t內（△t=N·dt）插值得到d t的系泊纜索響應對應的浮體響應，計算其頂端張力FM（t）并通過導纜孔傳遞信息，實現不同時間間隔下浮體和系泊纜索耦合計算；

（6）判斷計算時間t是否結束，如未結束繼續重復前面2～5步，到達預定時間Tset，程序結束。

圖2 系泊浮體物面非線性時域耦合計算的流程圖Fig.2 Flowchartof the body nonlinear time domain coupling calculation of amooring floating body

2.1 邊界積分方程的離散

采用面元法對時域邊界方程（21）進行數值離散，在物面SB（t）上劃分網格數量NB（t）塊，水線wl（τ）上劃分數量Nw（t）份。假設每個面元和水線單元上的速度勢為定值。離散的時域邊界積分方程可以寫為

式中的影響系數矩陣可以寫為：

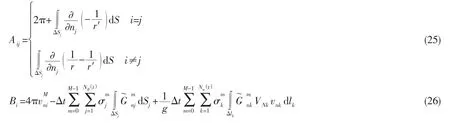
式中：時間間隔為Δt，記t=MΔt，τ=mΔt。Bi為記憶效應的卷積項，每時刻需要重新計算。求解離散的線性代數方程（24），得到浮體物面源強，進而求解浮體時域水動力問題。

2.2 瞬時濕表面網格產生方法

圖3中（a）～（f）依次給出了瞬時濕表面網格的每時刻重新劃分的過程，主要用于處理通常為均勻柱體或箱體的系泊浮體。首先將初始時刻浮體底部網格正常劃分，而側壁網格只進行周向劃分，垂向暫不劃分。利用轉換矩陣［B］[27]將初始平衡狀態網格進行轉換。由于物面非線性理論滿足線性自由面條件，時域擾動力在瞬時平均濕表面進行計算，因此采用平均靜水面Z=0切割瞬時運動姿態的浮體。隨后利用逆矩陣［B］-1將網格扶正進行側壁垂向網格劃分。最后利用轉換矩陣［B］得到時刻t的瞬時濕表面網格。該方法每時刻得到的網格節點數和單元數不變，適用于系泊浮體搖蕩角度不大情況。

圖3 網格單元更新實施過程Fig.3 Themesh elements regeneration implementation process

2.3 異步耦合方法

通常浮體和系泊纜索的響應采用相同時間間隔，即取滿足系泊纜索響應的較小時間間隔，這會使浮體響應的計算效率較低。本文采用異步耦合方法將浮體和系泊纜索劃分為兩個獨立模塊，通過在導纜孔連接處更新傳遞位移和載荷信息，實現不同模塊的耦合計算。首先采用四階龍格庫塔法求解浮體時域運動方程，浮體位移和速度可以寫為：

式中：Δt為浮體運動時間間隔。通過tn，tn+Δt/2和tn+Δt時刻的值，得到時刻tn+Δt的解。然后使用異步耦合方法在浮體和系泊纜索各自最佳的時間間隔進行耦合計算，即Δt=N·d t，通常d t比Δt小一個量級。系泊纜索的載荷力是根據tn到tn+Δt/2或者tn+Δt/2到tn+Δt的小時間間隔tn+k·d t對應的浮體運動響應計算得到的。若浮體運動求解時間間隔Δt相對波浪和自身固有周期很小，平臺運動在tn和tn+Δt/2與tn+Δt/2和tn+Δt之間是光滑連續的。這樣可以采用三次樣條曲線作為插值函數[14]對浮體運動進行插值，得到小時間間隔tn+k·d t對應處的平臺位移，從而計算對應時間點處系泊纜索張力響應，完成系泊浮體和系泊纜索的動力耦合步進求解。圖4給出了異步耦合方法示意圖。

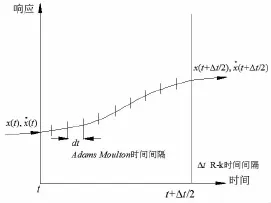
圖4 浮體異步耦合方法示意圖Fig.4 The sketch of asynchronous coupledmethod

3 數值算例結果及分析

3.1 系泊纜索動力響應

在系泊纜索頂端給定一個正弦運動的外部激勵，計算頂端張力FM變化的時歷曲線。系泊纜索的材質為鋼纜，其長度為762.0 m，名義直徑為0.14 m，單位長度的質量為235.2 kg/m，頂端預張力為1 558.8 kN，工作水深為223.5m。鋼纜頂端外部激勵的運動形式可以表示為

式中：X0為系泊纜索頂端初始橫坐標，A為運動幅值，ω為運動頻率。G（t）為緩載函數，G（t）=3α2-2α3，α=t/Tm，Tm為緩載時間。圖5和圖6分別給出了兩種工況參數下系泊纜索頂端張力響應的時歷曲線。將本文Adams-Moulton方法與Newmark-β方法以及基于集中質量方法的商業軟件Orcaflex的數值計算結果進行比較，可以看出三者的計算結果吻合度好，可以有效地分析系泊纜索動力問題。

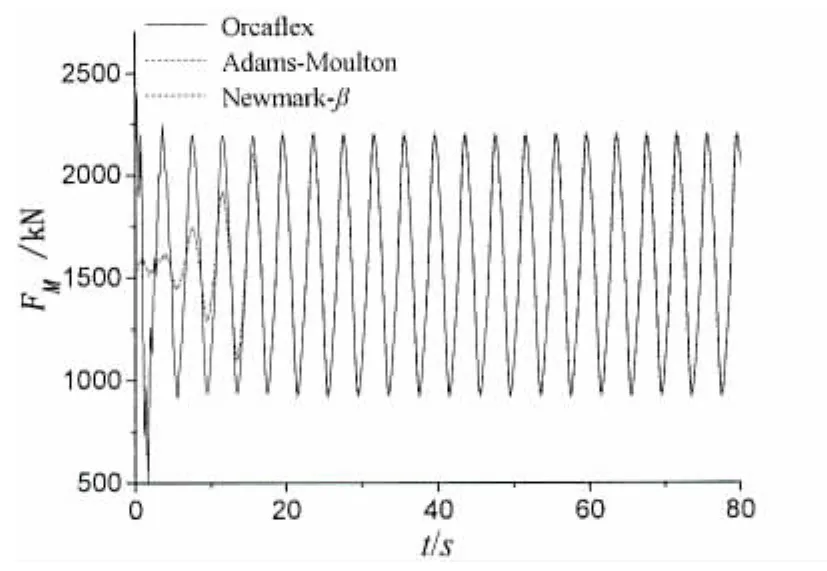
圖5 系泊纜索頂端張力時歷曲線，A=0.914 4m，T=4.0 sFig.5 Time history of the tension force of steel cable, A=0.914 4m,T=4.0 s

圖6 系泊纜索頂端張力時歷曲線，A=2.75m，T=8.0 sFig.6 Time history of the tension force of steel cable, A=2.75m,T=8.0 s

表2 半潛式平臺主要尺度參數Tab.2 The principal particular parameters of sem i-submersible platform

表3 半潛式平臺系泊系統主要參數Tab.3 Themain particulars ofmooring systems of sem i-submersible platform

3.2 系泊系統具體參數

半潛式平臺的工作水深為1 000.0m。表2給出了半潛式平臺主要尺度參數。圖5給出了半潛式平臺水動力計算網格模型。半潛式平臺系泊系統總共由12根錨泊纜索組成，分為4組，每組3根，表3給出系泊系統主要參數。圖8給出了半潛式平臺系泊系統的布置圖。該系泊系統下，半潛式平臺的縱蕩固有周期為255.5 s，垂蕩固有周期為19.0 s，縱搖固有周期為25.5 s。

3.3 時域耦合動力分析

運用開發的深海系泊浮體物面非線性時域耦合分析數值程序對深海系泊半潛式平臺在二階非線性不規則波作用下分別進行耦合響應分析。采用時域格林函數直接時域耦合方法在平臺瞬態位置對系泊系統分別進行了物面非線性時域耦合靜力響應（Body Nonlinear Time Domain Static Coupling,BNTD_SC）分析和物面非線性時域耦合動力響應（Body Nonlinear Time Domain Dynamic Coupling,BNTD_DC）分析。兩者都在瞬態位置計算作用于系泊浮體上的水動力載荷。不同之處在于前者在瞬態導纜孔位置只考慮了系泊纜索的恢復力，而后者考慮了系泊纜索的恢復力、拖曳阻尼力和慣性力引起的動態效應。同時將基于平均濕表面的常規間接時域方法動力耦合響應（Indirect Time Domain Dynamic Coupling,ITD_DC）和物面非線性時域耦合動力響應（BNTD_DC）的數值模擬結果進行比較。兩者都在瞬態導纜孔位置考慮系泊纜索動態效應。不同之處在于前者基于平均濕表面利用攝動展開方法進行一階和二階水動力計算，忽略了浮體低頻漂移和轉動造成位置變化對水動力及系統動力響應的影響，而后者基于瞬態位置濕表面進行水動力計算，將波頻運動和低頻運動一致求解。其中，基于平均濕表面位置計算深海系泊浮體動力耦合響應的數值程序已與國際通用商業軟件AQWA進行了比較驗證[15-16]。

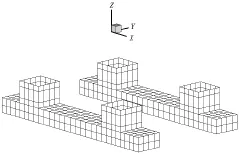
圖7 半潛式平臺水動力的計算網格Fig.7 Mesh grid model of semi-submersible platform

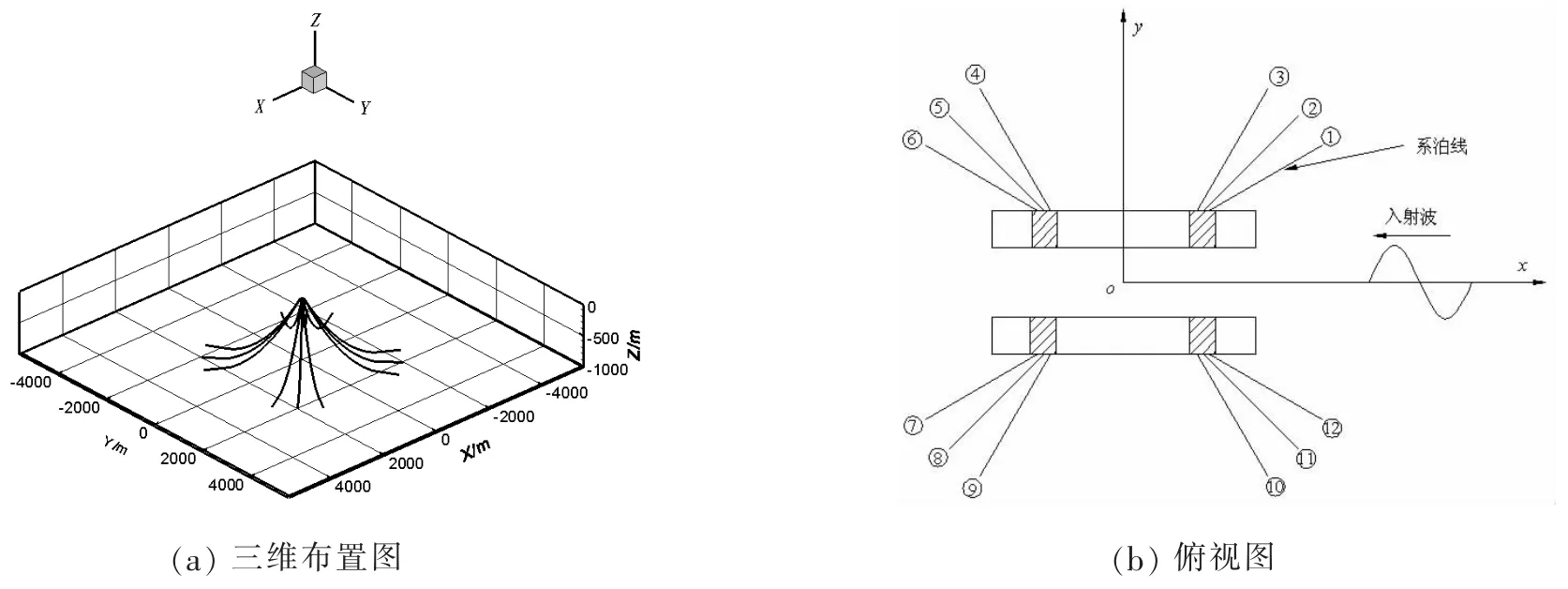
圖8 半潛式平臺系泊系統的布置圖Fig.8 The layoutof themooring system of semi-submersible platform

系泊浮體在初始時刻t=0靜止對流場沒有影響，流場處于未擾動狀態。當t>0時，加入物面邊界條件式（15），物體發生運動使流場處于擾動狀態。為了減小突然加入物面邊界條件在時域數值模擬中帶來的初始效應影響，在其右端乘上光滑函數Y（t）[32]用來描述速度勢隨時間和空間逐漸發展的過程，可以寫為

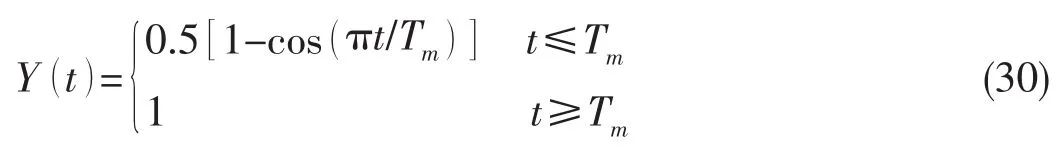
式中：光滑時間為Tm，通常為波浪周期的數倍。

圖9 JONSWAP波能譜Fig.9 JONSWAPwave spectrum

大地坐標系下，平臺重心初始位置為0.0 m，0.0m，0.33m，轉動角度均為零。平臺的動力學時間間隔為△t=0.3 s，系泊纜索的動力學時間間隔為d t=0.05 s。每根系泊纜索劃分30個單元用于系泊纜索有限元計算。平臺分析初始浪向為迎浪β=180。采用JONSWAP波浪譜模擬南海不規則波浪。一年一遇工況參數為有義波高Hs為6.0m，譜峰周期Ts為11.2 s，譜峰因子γ為3.33；百年一遇工況參數為有義波高Hs為13.3m，譜峰周期Ts為15.5 s，譜峰因子γ為3.33。圖9給出了兩種工況參數的JONSWAP波浪譜。

圖10為一年一遇工況下半潛式平臺運動響應時歷曲線。從圖中可以看出，平臺縱蕩波頻運動幅度很小，漂移力使得平臺偏離初始平衡位置，伴隨平臺固有周期的大幅低頻慢漂運動。間接時域耦合動力響應（ITD_DC）和物面非線性時域耦合動力響應（BNTD_DC）對系泊系統的計算結果趨勢基本一致，吻合度好。還可以看出，物面非線性時域耦合靜力響應（BNTD_SC）和動力響應（BNTD_DC）的低頻運動具有類似固有周期，但由于系泊纜索的動力效應導致平臺運動響應幅值差異較大，靜力響應比動力響應的結果偏大。系泊纜索對平臺垂蕩和縱搖運動的影響并不非常明顯，主要體現為波頻運動，靜力響應和動力響應的結果相差不大。

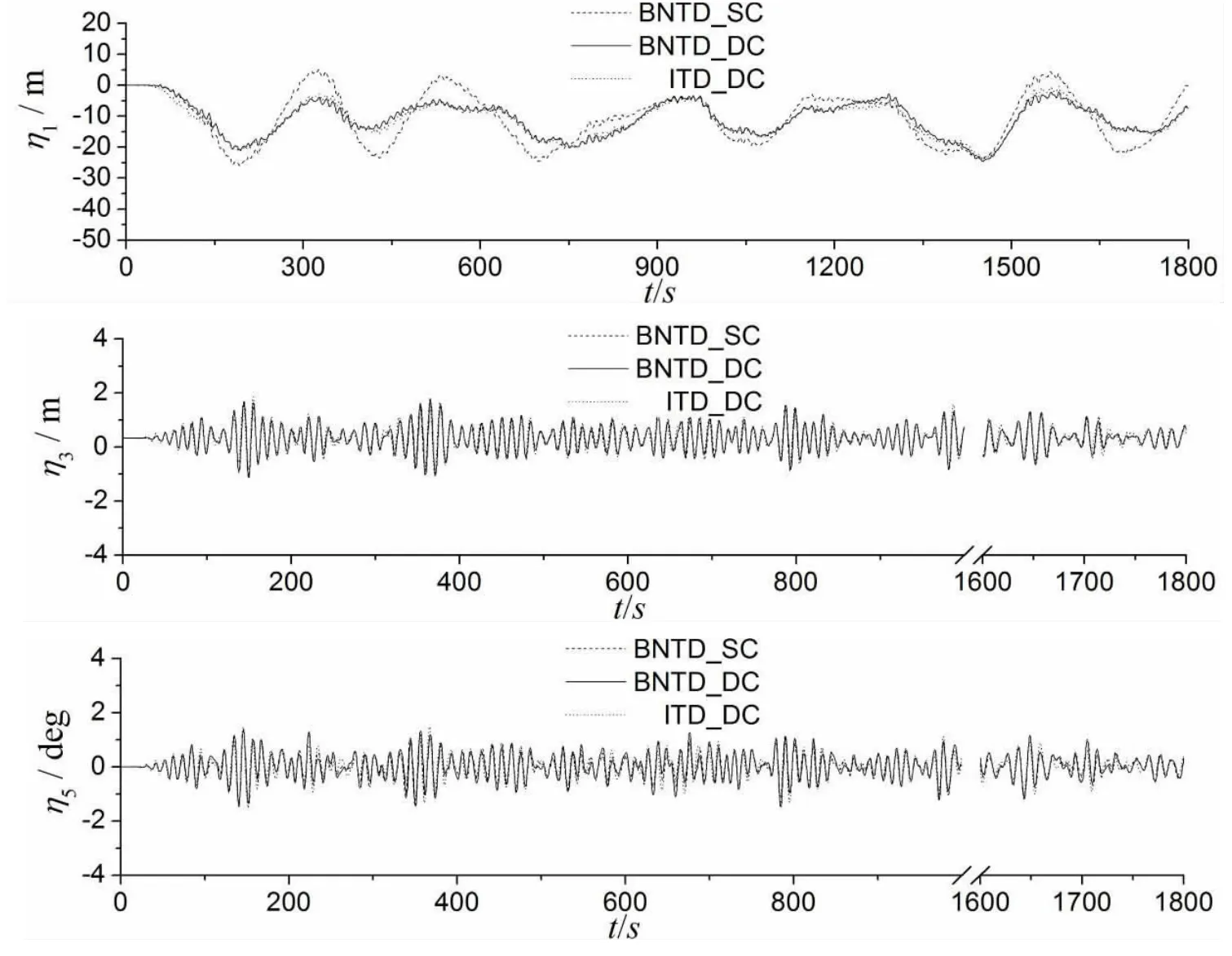
圖10 半潛式平臺的時域運動響應時歷曲線，Hs=6.0m，Ts=11.2 s，β=180°Fig.10 Time history ofmotion responses of the semi-submersible platform，Hs=6.0m,Ts=11.2 s,β=180°

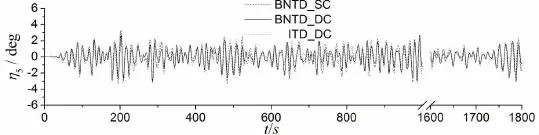
圖11 半潛式平臺的時域運動響應時歷曲線，Hs=13.3m，Ts=15.5 s，β=180°Fig.11 Time history ofmotion responses of the semi-submersible platform,Hs=13.3m,Ts=15.5 s,β=180°

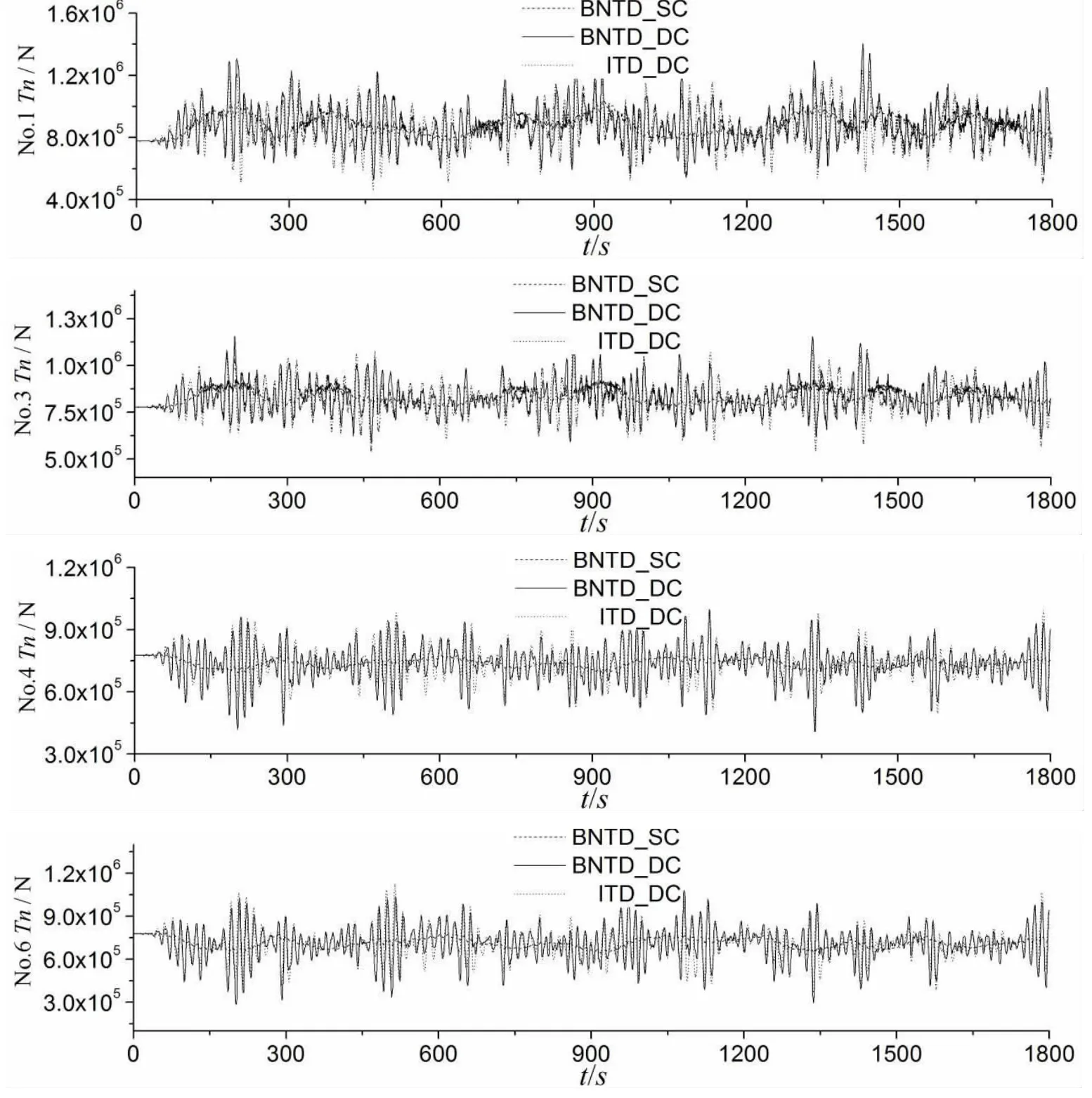
圖12 系泊纜索張力響應時歷曲線，Hs=13.3m，Ts=15.5 s，β=180°Fig.12 Time history of tensions of themooring lines，Hs=13.3m,Ts=15.5 s,β=180°

圖11為百年一遇工況下半潛式平臺運動響應時歷曲線。由于海況加大，整個系泊系統的運動響應明顯增大。間接時域耦合動力響應（ITD_DC）和物面非線性時域耦合動力響應（BNTD_DC）對系泊系統的計算結果趨勢基本一致，但兩種水動力計算模型結果存在差異。前者基于平臺的平均濕表面對系泊平臺進行水動力計算分析，首先計算一階波頻運動，然后在此基礎上確定二階低頻運動，沒有實現完全耦合計算水動力；而后者基于平臺的瞬態實時空間位置濕表面，將系泊平臺的波頻運動和低頻運動一致求解進行水動力計算分析。

從系泊系統布置圖8中可以發現在迎浪下的系泊系統具有對稱性，按照對稱性選系泊纜索No.1，No.3，No.4和No.6為研究對象。圖12給出了百年一遇工況下系泊纜索頂端張力響應時歷曲線。從圖中可以看出，系泊纜索頂端的張力變化和平臺縱蕩運動變化趨勢類似，它很大程度依賴于縱蕩運動模態。還可以發現出，不同位置的系泊纜索頂端張力響應存在差異。在波浪漂移力作用下，處于迎浪面的系泊纜索No.1頂端張力響應最大，其最大響應比預張力大約為82%；背浪面的系泊纜索No.6頂端張力響應最小，其最大響應比預張力大約為30%。這表明該系泊系統在百年一遇海況下安全系數高，穩定性好。

3.4 運動響應譜分析與統計分析

圖13給出了一年一遇工況下半潛式平臺的運動響應譜。從圖中可以看出，不規則波作用下平臺縱蕩運動在ω=0.025 rad/s附近存在明顯低頻運動特性，而在波頻范圍內幾乎沒有響應峰值；平臺垂蕩運動則在ω=0.53 rad/s的波頻附近出現響應峰值；平臺縱搖運動不僅存在波頻響應峰值，還在ω=0.25 rad/s的縱搖固有頻率附近出現低頻響應峰值。還可以發現，三種方法在波頻范圍內結果吻合較好，低頻運動響應存在差別，與之前分析物面非線性時域耦合靜力響應（BNTD_SC）和動力響應（BNTD_DC）的結果差別原因一致。

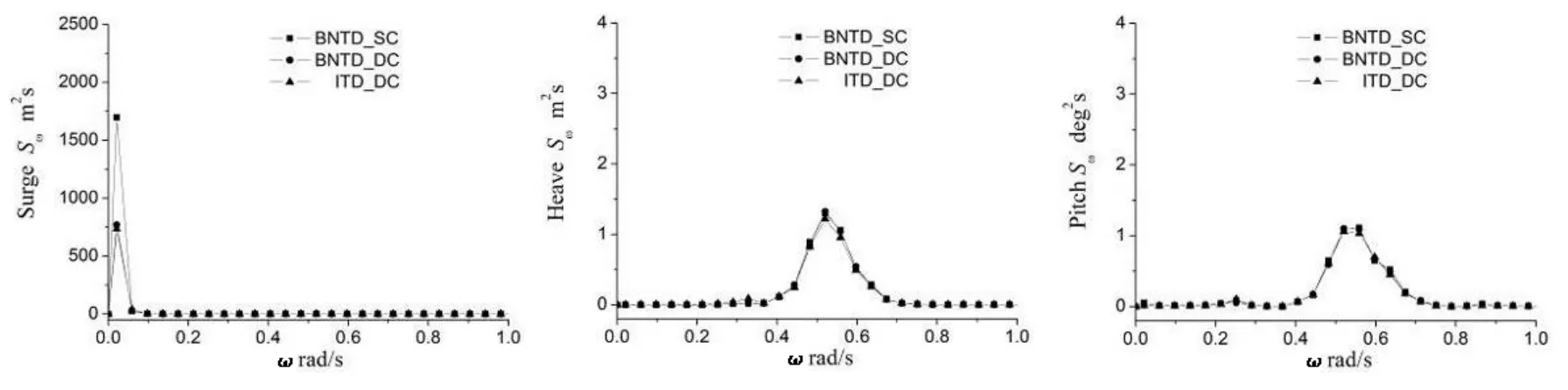
圖13 半潛式平臺運動響應譜，Hs=6.0m，Ts=11.2 s，β=180°Fig.13 Themotion responses spectra of the semi-submersible platform，Hs=6.0m,Ts=11.2 s,β=180°

圖14 半潛式平臺運動響應譜，Hs=13.3m，Ts=15.5 s，β=180°Fig.14 Themotion responses spectra of the semi-submersible platform，Hs=13.3m,Ts=15.5 s,β=180°

圖14給出了百年一遇工況下半潛式平臺的運動響應譜。從圖中可以看出，平臺縱蕩運動不僅存在低頻響應峰值，還在ω=0.4 rad/s出現相對較小波頻響應峰值；平臺垂蕩運動除低頻運動外還在ω= 0.33 rad/s垂蕩固有頻率附近出現明顯低頻響應峰值；平臺縱搖運動譜特性與工況1類似。雖然垂蕩和縱搖運動受系泊纜索影響較小，但垂蕩運動低頻響應差異最為顯著。這是由于間接時域耦合動力響應（ITD_DC）是基于系泊浮體平均濕表面通過二次傳遞函數QTF在頻域中計算得到低頻響應，而物面非線性時域耦合動力響應（BNTD_DC）是基于系泊浮體瞬態位置將平臺波頻運動和低頻運動一致求解，低頻響應激勵來自于非線性水動力中的低頻貢獻。可以發現，平臺在百年一遇海況中垂蕩運動響應明顯，每時刻平臺吃水不斷變化，平臺瞬時空間位置對垂蕩低頻運動影響比較大。

圖15和圖16分別給出了一年一遇和百年一遇工況作用下下半潛式平臺的運動響應統計分析結果。從圖中可以看出，縱蕩運動由于漂移力的影響，平臺會產生X軸負向偏移，平均值基本相同。由于系泊纜索動力效應，物面非線性時域耦合靜力響應（BNTD_SC）縱蕩運動的最大值和最小值與動力響應（BNTD_DC）相差較大。平臺垂蕩運動和縱搖運動響應的統計特性結果基本一致。

圖15 半潛式平臺運動響應統計分析，Hs=6.0m，Ts=11.2 s，β=180°Fig.15 The statistical analysis results formotion responses of the semi-submersible platform,Hs=6.0m,Ts=11.2 s,β=180°

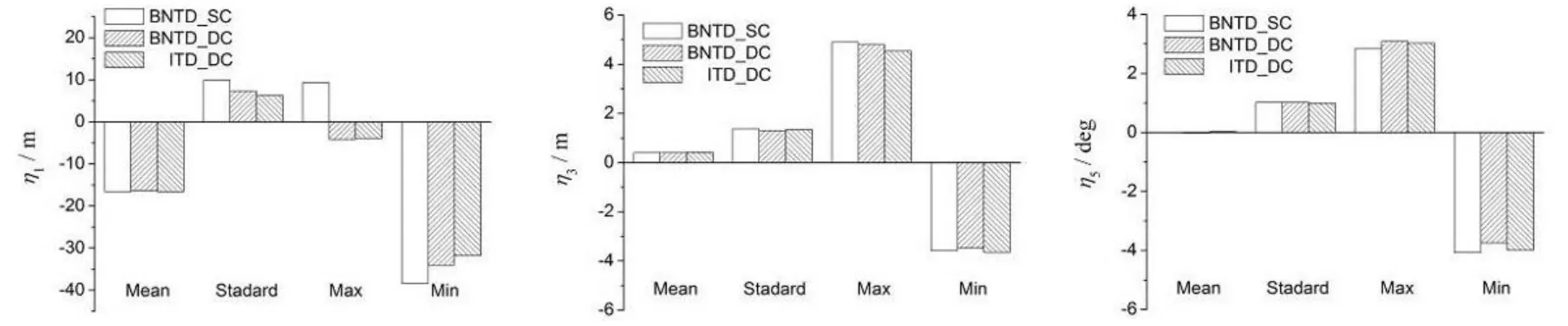
圖16 半潛式平臺運動響應統計分析，Hs=13.3m，Ts=15.5 s，β=180°Fig.16 The statistical analysis results formotion responses of the semi-submersible platform,Hs=13.3m,Ts=15.5 s,β=180°

4 結 論

本文基于三維時域勢流理論和彈性細長桿理論，研究并提出了深海系泊浮體物面非線性時域耦合動力分析方法，建立了深海系泊浮體物面非線性時域耦合數學模型。該方法采用時域格林函數物面非線性理論方法在瞬態位置直接時域模擬系泊浮體所需水動力，采用有限元方法計算系泊纜索的動力響應，利用異步耦合方法在各自最佳時間間隔求解系泊浮體時域運動方程和系泊纜索動力方程，通過在導纜孔處傳遞浮體運動響應和系泊纜索張力信息，實現了兩者時域動力耦合求解。通過對二階非線性不規則波作用下深海系泊半潛式平臺時域耦合響應特性進行研究，將不同海況下物面非線性時域耦合靜力和動力響應與間接時域耦合動力響應的三種計算方法結果相比較。研究結果表明，系泊纜索動力響應明顯，平臺瞬態空間位置對低頻運動影響較大，有必要在平臺瞬時濕表面采用動力響應方法進行深海系泊浮體時域耦合響應分析。

[1]Lee M Y,Flory J.ABSguide for synthetic ropes in offshoremooring applications[C].OTC,10910,1999.

[2]MaW,Lee M Y,Zou J,Huang EW.Deepwater nonlinear coupled analysis tool[C].OTC,12085,2000.

[3]Lee M Y,Devlin P.Developmentof APIRP 2SM for synthetic fiber ropemoorings[C].OTC,12178,2000.

[4]Kim M H,Tahar A,Kim Y B.Variability of sparmotion analysis against various designmethodologies/parameters[C].Proceedings of the 20th Offshore Mechanics and Artic Engineering Conference,2001.

[5]Kim M H,Tahar A,Kim Y B.Variability of TLPmotion analysis against various design methodologies/parameters[C].Proceedings of the 8th International Offshore and Polar Engineering Conference,2001:467-473.

[6]Low Y M,Langley R S.Time and frequency domain coupled analysis of deepwater floating production systems[J].Applied Ocean Research,2006,28:371-385.

[7]Low Y M.Prediction of extreme responses of floating structures using a hybrid time/frequency domain coupled analysis approach[J].Ocean Engineering,2008,35:1416-1428.

[8]Ran Z.Coupled dynamic analysis of floating structures in waves and current[D].Ph.D.thesis,Texas University,2000.

[9]Kim M H.Vessel/mooring/riser coupled dynamic analysis of a turret-moored FPSO compared with OTRC experiment[J]. Ocean Engineering,2005,32:1780-1802.

[10]Garrett D L.Coupled analysis of floating production systems[J].Ocean Engineering,2005,32:802-816.

[11]Yang C K,Kim M H.Transient effect of tendon disconnection of a TLP by hull-tendon-riser coupled dynamic analysis [J].Ocean Engineering,2010,37:667-677.

[12]馮愛春,尤云祥,范 菊.不規則波中半潛式平臺及其系泊系統動力響應分析[J].海洋工程,2010,28(3):31-36. Feng A C,You Y X,Fan J.Dynamic characteristics of a semi-submersible platform withmooring system in irregular waves [J].Ocean Engineering,2010,28(3):31-36.

[13]鄭成榮,范 菊,繆國平,等.深海FPSO時域耦合動力分析[J].水動力學研究與進展,2012,27(4):376-382. Zheng C R,Fan J,Miao G P,et al.Dynamic characteristics of a semi-submersible platform with mooring system in irregularwaves[J].Chinese Journal of Hydrodynamics,2012,27(4):376-382.

[14]Jing X N,WebsterW C,Xu Q,Lambrakos K.Coupled dynamic modeling of amoored floating platform with risers[C].Proceedings of the ASME 2011 30th Interactional Conference on Ocean,Offshore and Arctic Engineering,OMAE2011-49553.

[15]Ma S,Duan W Y,Yang Z G.Asynchronous coupled analysis of a single pointmoored FPSO[C]//Proceedings of the 10th Interactional Conference on Hydrodynamics.Saint-Petersburg,Russia,2012:251-258.

[16]馬 山,段文洋.深海浮動式平臺與系泊/立管系統動力響應異步耦合分析研究[C]//第二十五屆全國水動力學研討會暨第十二屆全國水動力學學術會議論文集.中國,浙江舟山,2013:786-792.

[17]劉文璽,周其斗,張緯康,等.浮體與系泊系統的耦合動力分析[J].船舶力學,2014,18(8):940-957. Liu W X,Zhou Q D,ZhangW K,et al.Dynamic analysis of the coupled floating body/mooring system[J].Journal of Ship Mechanics,2014,18(8):940-957.

[18]唐友剛,易 叢,張素俠.深海平臺系纜形狀和張力分析[J].海洋工程,2007,25(2):9-14. Tang Y G,Yi C,Zhang SX.Analysis of cable shape and cable tension for platforms in deep sea[J].Ocean Engineering, 2007,25(2):9-14.

[19]Garrett D L.Coupled analysis of floating production systems[J].Ocean Engineering,2005,32:802-816.

[20]Yang M D,Teng B.Static and dynamic analysis ofmooring lines by nonlinear finite elementmethod[J].China Ocean Engineering,2010,24(3):417-430.

[21]肖 越.系泊系統時域非線性計算分析[D].大連:大連理工大學,2005.

[22]耿寶磊.波浪對深海海洋平臺作用的時域模擬[D].大連:大連理工大學,2010.

[23]袁 夢.深海浮式結構物系泊系統的非線性時域分析[D].上海:上海交通大學,2010.

[24]Teng B,Yang M D.Nonlinear coupled dynamic analysis for waves and amoored platform in time domain[C]//Proceedings of the 26th internationalworkshop on waterwaves and floating bodies.Athens,Greece,2011.

[25]Yang M D,Teng B,Ning D,Shi Z.Coupled dynamic analysis for wave interaction with a truss spar and itsmooring line/ riser system in time domain[J].Ocean Engineering,2012,39:72-87.

[26]Kim JW,Izarra R,Jang H,Kyoung J,O’Sullivan J.An application of the EMO-based numerical basin to dry-tree semisubmersible design[C]//Proceedings of the 19th Offshore Symposium.Houston,Texas,2014.

[27]Liu SK,Papanikolaou A.Time-domain hybrid method for simulating large amplitudemotions of ships advancing in waves [J].Journal of the Korean Society of Naval Architects and Ocean Engineering,2011,3(1):72-79.

[28]戴遺山,段文洋.船舶在波浪中運動的勢流理論[M].北京:國防工業出版社,2008.

[29]黃德波.時域Green函數及其導數的數值計算[J].中國造船,1992,4:16-25. Huang D B.Approximation of time-domain free surface function and its spatial derivatives[J].Shipbuilding of China,1992, 4:16-25.

[30]段文洋.船舶大幅運動非線性水動力研究[D].哈爾濱:哈爾濱工程大學,1995.

[31]馬 剛.基于彈性細桿理論的深海立管和系泊線動力學模型研究[D].哈爾濱:哈爾濱工程大學,2009.

[32]Xu G,Duan W Y.Time-domain simulation ofwave-structure interaction based onmulti-transmitting formula coupled with damping zonemethod for radiation boundary condition[J].Applied Ocean Research,2013,42:136-143.

Body nonlinear time domain coup led dynam ic analysis of amooring floating body in deepsea

HAN Xu-liang1,2,DUANWen-yang2,MA Shan2,XIE Bin1
(1.CNOOCResearch Institute,Beijing 100028,China;2.College of Shipbuilding Engineering, Harbin Engineering University,Harbin 150001,China)

Based on the three-dimensional time domain potential flow theory and the slender rod theory, the body nonlinear time domain coupled dynamic analysismethod of amooring floating body is investigated and proposed.The transient free surface Green functionmethod was extended and applied to simulate the transient position hydrodynamic calculation of amooring offshore structure in waves.The finite elementmodel is employed to solve dynamic responses ofmooring lines.Then asynchronous coupled method is adopted to achieve the coupled dynamic analysis of a floating body and mooring lines,which satisfies the hydrodynamic coupling calculation of amooring floating body in time domain,and the dynamic coupling between a floating body andmooring lines.The time domain coupled responses analysis program is applied for amooring semi-submersible platform in the second order nonlinear irregular waves.Both body nonlinear time domain static coupling responses and dynamic coupling responses numerical simulation results,including motion responses of platform and tension responses ofmooring lines,are presented and compared with the traditional indirect time domain dynamic coupling responses approach in different random sea conditions.The results show that the dynamic coupling effects are significant and the transient position hydrodynamic cal-culation of platform has a great influence on the low frequencymotion especially on heavemotion.So it is necessary to coupled dynamic analysis of amooring floating body with transient position hydrodynamic calculation in deep sea.

transient free surface Green function;body nonlinear;time domain coupled;dynamic responses;slender rod theory

U661.1

：Adoi:10.3969/j.issn.1007-7294.2017.01.005

2016-06-15

國家自然科學基金資助項目（51079032）；國家自然科學基金資助項目（51109040）

韓旭亮（1985-），男，博士，E-mail：hanxuliang112@yahoo.com；

段文洋（1967-），男，教授，博士生導師。

1007-7294（2017）01-0031-14