耐壓殼體局部腐蝕穩定性計算方法
向楊君,卞如岡
(中國船舶科學研究中心,江蘇 無錫 214082)
耐壓殼體局部腐蝕穩定性計算方法
向楊君,卞如岡
(中國船舶科學研究中心,江蘇 無錫 214082)
文章提出了可以計及局部腐蝕損傷影響的等效層合單元方法,建立了局部腐蝕等效彈性模量計算公式,針對耐壓殼體局部腐蝕深度、腐蝕強度、腐蝕范圍和初撓度進行了系列穩定性數值計算,通過計算結果的對比分析提出了將局部腐蝕等效為附加多波撓度的穩定性近似計算方法,給出了附加撓度幅值的計算公式,可用于耐壓殼體局部腐蝕的穩定性分析。
局部腐蝕;等效層合單元;附加撓度
0 引 言
耐壓殼體在工程實際中已得到大量應用,老齡殼體結構多數存在嚴重的腐蝕問題。除均勻腐蝕以外,局部腐蝕(又稱非均勻腐蝕)是常見且危害極大的一種,它是由于金屬表面物理和化學的不均勻性所引起的。嚴重的局部腐蝕可能大大降低結構的承載能力,引起嚴重的安全事故,因此,開展局部腐蝕對結構承載能力的影響研究是極其必要的[1]。
耐壓殼體坑點腐蝕影響作為典型的結構局部腐蝕問題,國內外學者及相關機構已經做了大量的研究。TSCF[2]、Daidora[3]等開展了坑點腐蝕鋼板等效厚度及剩余厚度計算方法研究,Flaks[4]、Paik[5]開展了坑點腐蝕對受拉鋁板和船舶極限強度的影響研究,并認為在評估結構強度時,坑點腐蝕所造成的截面積損失是比坑點腐蝕深度更值得關注的指標。Smith[6]、Jiang[7]、MacKay[8]等分別通過試驗和數值方法考察了局部腐蝕導致的耐壓殼體殼板減薄對結構失穩壓力的影響。徐強、萬正權[9-10]開展了坑點腐蝕板的等效材料常數研究,并基于線彈性理論推導了含坑點腐蝕的殼體有限元計算方法。邱昌賢等[11]將Monte Carlo抽樣法和有限元非線性屈曲計算相結合,分析了腐蝕量均值和方差對結構在靜水外壓下極限承載能力的影響。
由于局部腐蝕結構損傷的復雜性,通過傳統的理論研究以求獲得精確的解析解是一項非常困難的工作。本文采用有限元數值計算與理論分析相結合的方法,建立了局部腐蝕等效彈性模量計算公式,提出了簡便可行的局部腐蝕等效層合單元方法,能夠有效地考慮局部腐蝕對耐壓殼體結構的強度與穩定性影響。針對耐壓殼體結構進行了系列穩定性計算分析,在此基礎上提出了將局部腐蝕等效為附加撓度的穩定性計算方法及附加撓度幅值計算公式。
1 計算方法
1.1 等效層合單元
等效層合單元(Equivalent Layered Element)采用分層力學模型,將腐蝕結構分為腐蝕層和完好層,腐蝕層的材料常數取等效的力學參數。
實踐中可以直接利用相關有限元軟件中的層合單元(SHELL181,SOLID185等)進行結構建模計算。本文選取通用有限元軟件ANSYS中的SHELL181單元進行建模計算,為了取得更加逼真的腐蝕效果,可以將腐蝕結構設置為兩層或兩層以上,此處僅限于討論兩層的情況。
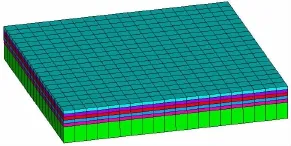
圖1 等效層合單元Fig.1 The equivalent layered element

圖2 坑點腐蝕幾何模型Fig.2 Themodel of the local corrosion
局部腐蝕等效層合單元大大降低了數值計算時的復雜結構建模實施難度,從而可以方便高效地計算局部腐蝕對結構強度與穩定性的影響。
1.2 等效力學參數
目前,國內外學者對坑點腐蝕幾何形態的具體處理上還存在較大差異,如將蝕坑取為長方體坑、圓柱坑、球冠坑、半球形坑、圓錐坑等。為了盡可能真實地模擬耐壓殼體結構的坑點腐蝕,并考慮到腐蝕形狀的簡潔性,通常將殼體結構的坑點腐蝕優先處理成圓柱形,需要考慮的腐蝕參數主要包括蝕坑的半徑(r/h)、深度(h/t)和腐蝕強度DOP。其中腐蝕強度DOP等于腐蝕面積與單元面積的比值,即

式中:Ai是第i個蝕坑的面積,n為蝕坑個數,A為單元面積。
為了將局部腐蝕結構的腐蝕層進行等效,必須賦予腐蝕層等效力學參數。本文根據基于等效應變假設的理論分析和數值計算結果,給出腐蝕層等效彈性模量的計算公式:
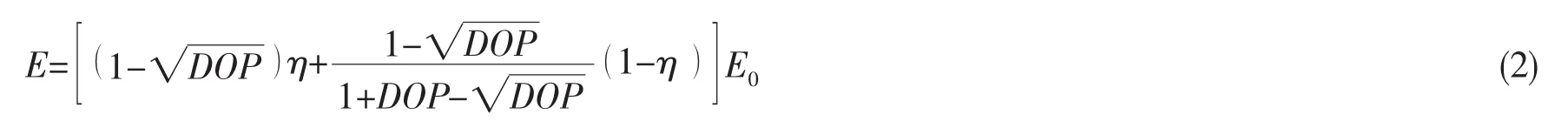
其中:η表示等效系數,對于鋼結構通常情況下可以取η=DOP0.15。
該計算公式結果與文獻[9]中試驗數據相符合,對于不同的腐蝕強度,等效彈性模量計算值如圖3所示。
當需要考慮計及腐蝕損傷層和完好層的整個結構的等效彈性模量時,同樣可以應用等效應變假設,得到如下的計算公式:
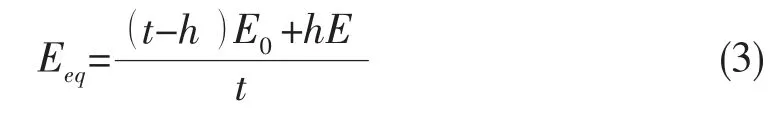
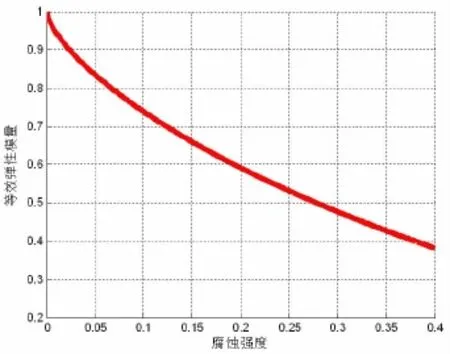
圖3 等效彈性模量計算值Fig.3 The results of themodulus of elasticity
2 計算模型
本文選取含局部腐蝕的耐壓圓柱殼作為計算對象,其有限元模型如圖4所示。結構材料彈性模量E0=1.96×105MPa,泊松比μ=0.3,u=1.68,β=5.78。
模型全部采用SHELL181單元劃分網格,在周向上網格密度與角度一致,局部腐蝕夾角度數θ即為腐蝕單元的周向分布數,局部腐蝕位于試驗段的肋骨之間,并沿圓柱殼周向分布。
無損傷的結構特征值屈曲載荷P=0.011 36σs,失穩波數13,非線性計算中初撓度和附加撓度取值為相應的幅值乘以特征值失穩波形。

圖5 結構特征值屈曲Fig.5 The eigenvalue buckling displacement
3 有限元計算分析
本文采用局部腐蝕等效層合單元方法,針對計算模型進行一系列穩定性數值計算,在局部腐蝕有限元計算中,可能影響臨界壓力的參數主要有:腐蝕深度(h/t)、腐蝕強度DOP、腐蝕范圍θ和結構初撓度幅值 f0。
局部腐蝕范圍對結構承載能力影響的有限元計算結果如表1與圖7所示,在腐蝕范圍的擴展過程中,局部腐蝕結構的穩定性承載能力并不隨腐蝕范圍的增大而明顯變化,而是基本保持穩定。因此在計及局部腐蝕的承載能力計算中,可以將腐蝕范圍θ取為某一不變量。圖6所示為腐蝕深度0.2t,腐蝕強度0.15,腐蝕范圍13°時的結構失穩狀態。
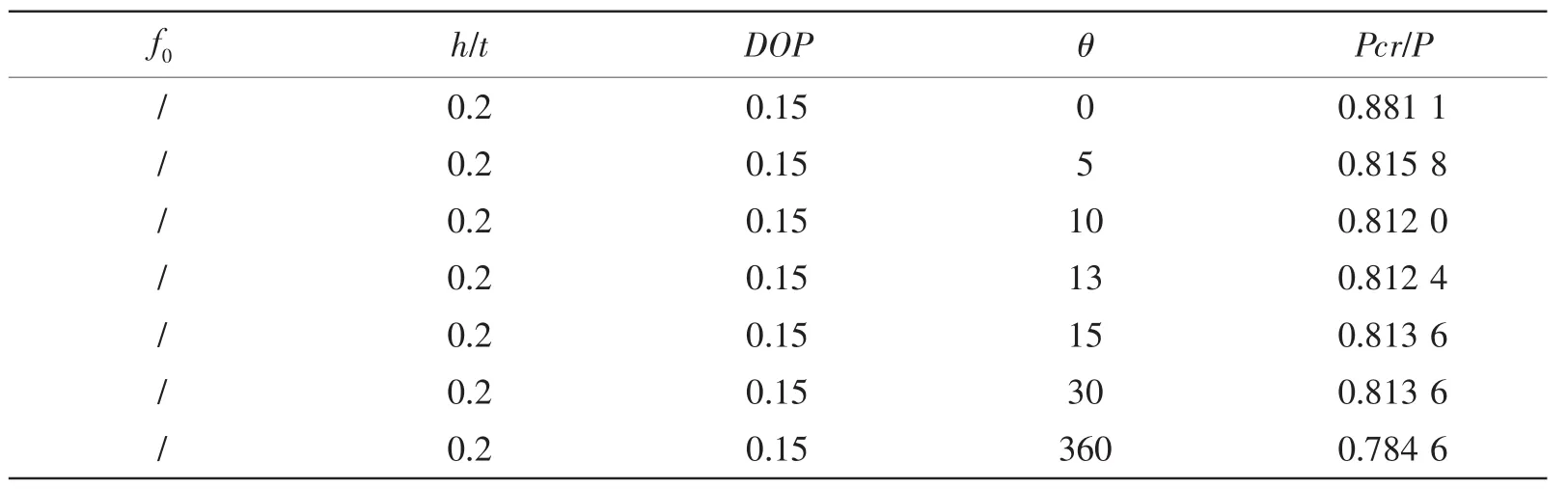
表1 腐蝕范圍有限元計算結果Tab.1 The resultw ith respect to range of corrosion
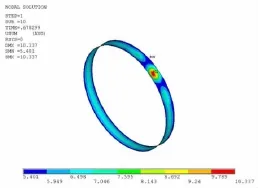
圖6 腐蝕范圍失穩狀態 Fig.6 Collapse state with corrosion(θ=13°)
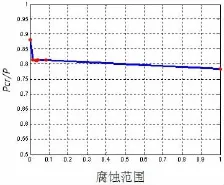
圖7 腐蝕范圍影響曲線Fig.7 The influence curve of range
局部腐蝕深度及強度對結構承載能力影響的有限元計算結果如表2與圖9所示,由此可見腐蝕深度和腐蝕強度作為影響結構受力橫截面大小的主要因素,共同對腐蝕結構的穩定性承載能力施加影響,結構承載能力隨著兩者的增大而減小。當腐蝕強度在0.3之內時,與腐蝕深度的影響基本一致,超過0.3之后腐蝕強度的影響變大。圖8所示為腐蝕深度0.2t,腐蝕強度0.15,腐蝕范圍15°的結構失穩狀態。
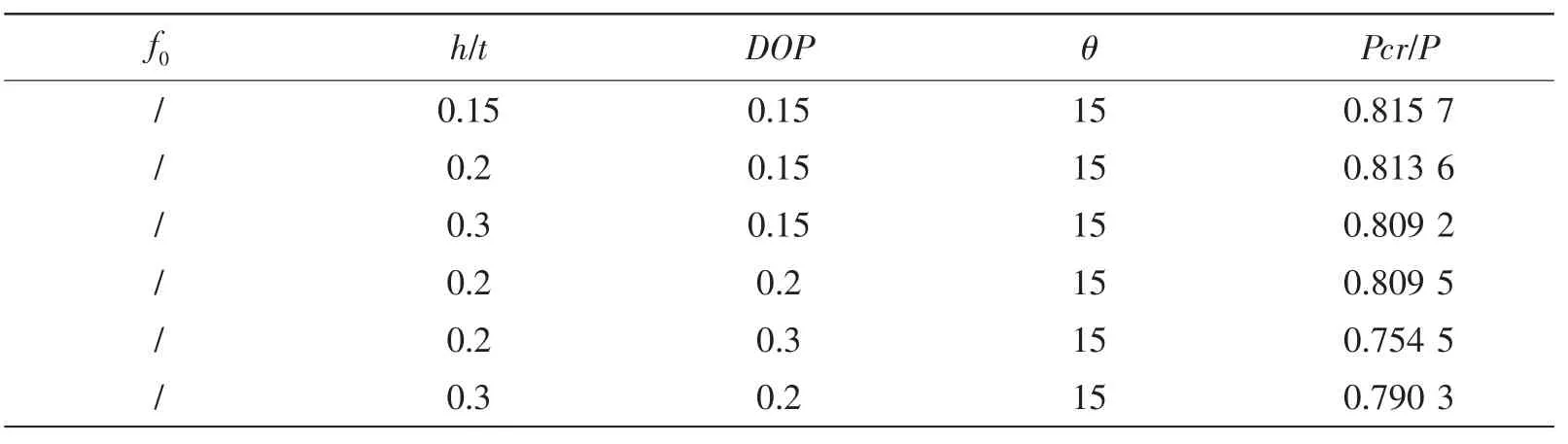
表2 腐蝕深度及強度有限元計算結果Tab.2 The resultw ith respect to deep and DOP of corrosion
局部腐蝕與0.2t幅值的多波初撓度共同作用時對結構承載能力影響的有限元計算結果如表3與圖11所示,由此可見當局部腐蝕與0.2t幅值的多波初撓度共同作用時,由于較大的初撓度的存在,使得局部腐蝕的影響變小,即圖11所示的三維圖中下方的計算結果的影響面幾乎成為一個平面。圖10所示為初撓度幅值0.2t,腐蝕深度0.2t,腐蝕強度0.15,腐蝕范圍15°時結構的失穩狀態。

表3 腐蝕與初撓度有限元計算結果Tab.3 The resultw ith respect to corrosion and initial deflection

續表3
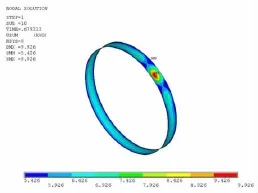
圖8 腐蝕深度與強度失穩狀態 Fig.8 Collapse statewith corrosion(h/t=0.2)
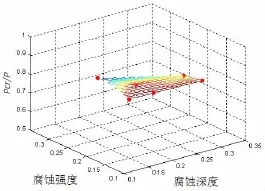
圖9 腐蝕深度與強度影響平面Fig.9 The influence plane of corrosion

圖10 腐蝕與初撓度失穩狀態Fig.10 Collapse statewith corrosion(f0=0.2)
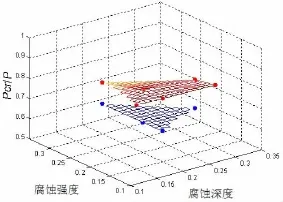
圖11 腐蝕與初撓度影響平面Fig.11 The influence plane of corrosion(f0=0.2)
結構初撓度對結構承載能力影響的有限元計算結果如表4與圖12所示,與上述表3計及局部腐蝕損傷的有限元結果比較可以發現,局部腐蝕損傷對結構穩定性承載能力的影響主要表現在對結構幾何非線性狀態的改變,且局部腐蝕損傷對結構穩定性承載能力的影響大小及趨勢與相應幅值的多波撓度對耐壓圓柱殼結構的影響基本一致,因此可以考慮將局部腐蝕等效為相應幅值的多波撓度進行近似計算。

表4 撓度大小有限元計算結果Tab.4 The result w ith respect to deflection

續表4
由于耐壓殼體加工初撓度總是不可避免地存在,且通常大于局部腐蝕對圓柱殼穩定性承載能力的影響,這就要求在進行局部腐蝕對耐壓殼體穩定性承載能力影響大小定量分析時,需要綜合考慮局部腐蝕以外的其它幾何非線性因素,其中最重要的即為初撓度的影響。
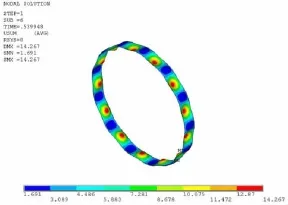
圖12 初撓度0.215t失穩狀態 Fig.12 Collapse statewith deflection(f=0.215)
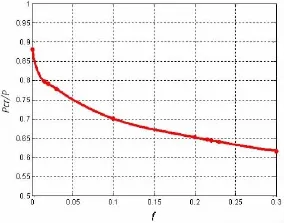
圖13 初撓度影響曲線Fig.13 The influence curve of deflection
4 近似計算方法
根據前述計算分析可知,局部腐蝕對結構穩定性承載能力的影響可以近似為相應幅值的多波撓度進行分析。因此考慮將局部腐蝕等效換算成具有等同影響效果的相應幅值的附加多波撓度進行穩定性計算分析,從而可以簡便快捷地計算出局部腐蝕結構的穩定性承載能力。
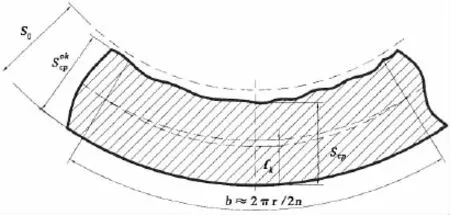
圖14 失穩半波長相當的殼板局部腐蝕區域Fig.14 A corrupt region equivalenthalf of buckling wavelength
局部腐蝕不僅會引起耐壓殼體殼板厚度變小,改變局部應力,而且會改變耐壓殼體的形狀。如圖14所示為失穩半波長相當的一段殼板局部腐蝕區域。
殼板外表面和內表面等距的中面位置確定耐壓殼體基本形狀,由于局部腐蝕對殼體殼板形狀的改變,與失穩半波長相當的單個區域的局部腐蝕在失穩時引起了中面的移動,從而形成了最大值為fk的殼板附加撓度。附加多波撓度幅值fk與局部腐蝕平均厚度hˉ之間有如下關系式:

局部腐蝕強度和腐蝕深度與腐蝕平均厚度之間具有如下關系式:

即有

公式(6)即為局部腐蝕參數與附加撓度之間的轉換公式。
由前述有限元計算結果可知,通過公式(6)得到的近似幅值的多波撓度對結構穩定性承載能力的影響大于相應的局部腐蝕損傷。如腐蝕深度0.2t,腐蝕強度0.2,腐蝕范圍15°時結構的穩定性承載能力為0.809 5P,而結構初撓度幅值為0.02t時的穩定性承載能力為0.791 8P;初撓度幅值為0.2t,腐蝕深度0.2t,腐蝕強度0.2,腐蝕范圍15°時結構的穩定性承載能力為0.649 4P,而結構初撓度幅值為0.22t時的穩定性承載能力為0.644 7P。究其原因,可能是因為附加撓度等效過程中將局部的殼板變形擴展為整個圓周上的多波撓度,即相當于擴大了局部腐蝕的范圍θ,而由表1和圖7所示的腐蝕范圍的計算分析結果可知,腐蝕范圍θ對結構穩定性承載能力的影響是有限的,說明該參數轉換計算公式是合理可行的。
因此,在對含局部腐蝕損傷的耐壓殼體穩定性承載能力進行計算時,可將初撓度幅值加上相應的局部腐蝕等效附加多波撓度幅值,再應用“考慮初始偏差的穩定性計算方法”進行結構穩定性計算分析即可,這將大大簡化含局部腐蝕結構的穩定性計算過程。
5 結 論
(1)本文提出了局部腐蝕等效層合單元(Equivalent Layered Element)方法,該方法能夠有效地用于含局部腐蝕損傷的耐壓殼體結構承載能力計算,具有較強的通用性和簡易性,可以有效地應用于類似結構的非線性計算分析之中。
(2)建立了等效彈性模量的計算公式,以局部腐蝕等效層合單元為基礎,展開了針對局部腐蝕參數的系列有限元計算,分析結果表明腐蝕深度(h/t)與腐蝕強度(DOP)是影響穩定性承載能力的主要因素。
(3)局部腐蝕對結構穩定性承載能力的影響主要表現為對結構幾何非線性狀態的改變,且與相應幅值的多波撓度類似,基于此本文確立了將局部腐蝕等效為附加多波撓度的穩定性近似計算方法,并建立了附加撓度幅值的計算公式。
[1]徐秉漢,朱邦俊,歐陽呂偉,等.現代潛艇結構強度的理論與試驗[M].北京:國防工業出版社,2007.
[2]TSCF.Experimental and theoretical investigation of the strength of corroded hull elements[R].Project 300,Report No.84-3438,Tanker Structure Co-operative Forum,1984.
[3]Daidora JC,Parente J,Orisamolu IR,Ma K T.Residual strength assessment of pitted plate panels[R].SSC-394,Ship Structure Committee,1997.
[4]Flaks V Y.Correlation of pitting corrosion of aluminum plates and reduction of load-beating capacity under tension[J]. Fiziko-Khimicheskaya Mekhanika Marerialov,1987,14(1):89-93.
[5]Paik JK,Lee JM,Ko M J.Ultimate shear strength of plate elementswith pit corrosion wastage[J].Thin-Walled Structures, 2004,42:1161-1176.
[6]Smith M J,MacKay JR.Overall elasto-plastic collapse of ring stiffened cylinderswith corrosion damage[J].Transactions of the Royal Institution of Naval Architects Part1A-International Journal of Maritime Engineering,2005.
[7]Jiang L,MacKay JR,Wallace J,Smith M J,Norwood M,Bosman T.Finite elementmodeling of collapse experiments of ring stiffened cylinderswith simulated corrosion damage[C].In Warship 2008:Naval Submarines 9.Glasgow:Royal Institution of Naval Architects,2008.
[8]MacKay JR.Experimental investigation of the strength of damaged pressure hulls-Phase 1[R].Defence Research and Development Canada-Atlantic,2007.
[9]徐 強,萬正權.含坑點腐蝕的殼體有限元計算方法[J].船舶力學,2010,14(1-2):84-93. Xu Qiang,Wan Zhengquan.Finite elementmethod of pitting corrosive shell[J].Journal of Ship Mechanics,2010,14(1-2):84-93.
[10]邱昌賢,萬正權,黃進浩.考慮腐蝕減薄的球殼開孔結構隨機有限元分析[J].船舶力學,2013,17(11):1269-1277. Qiu Changxian,Wan Zhengquan,Huang Jinhao.Stochastic finite element analysis for spherical shell with round hole in thinned conditions from corrosion[J].Journal of Ship Mechanics,2013,17(11):1269-1277.
Calculation method for stability of pressure hullw ith local corrosion
XIANG Yang-jun,BIAN Ru-gang
(China Ship Scientific Research Center,Wuxi214082,China)
Equivalent Layered Elementmethod is introduced to take into account the influence of local corrosion of pressure hull.The formula for equivalent elasticmodulus of plate with local corrosion is proposed. A series of numerical analysis for the corrosion depth,degree of pitting corrosion intensity,corrosion range and deflection are carried out.Finally,the approximate calculation method via additional deflection is established based on the contrast of stability analysis,and the formula for amplitude of additional deflection is presented.Thismethod is useful for stability analysis of pressure hullwith local corrosion.
local corrosion;Equivalent Layered Element;stability
U661.1
:Adoi:10.3969/j.issn.1007-7294.2017.01.008
2016-10-19
向楊君(1986-),男,工程師,E-mail:343714636.qq.com;
卞如岡(1970-),男,研究員。
1007-7294(2017)01-0061-08

