一種基于系統保形解耦的力源識別方法

王淑娟，王國巧，沈繼紅，韓偉民

（哈爾濱工程大學 理學院，哈爾濱150001）

一種基于系統保形解耦的力源識別方法

王淑娟，王國巧，沈繼紅，韓偉民

（哈爾濱工程大學 理學院，哈爾濱150001）

基于模態分析法的力源時域識別方法中涉及利用模態矩陣將系統方程轉化為非耦合形式，這僅對比例阻尼或經典阻尼系統才能實現。文章基于二階系統保結構解耦方法建立了新的力源識別數學模型。首先利用Lancaster結構建立系統的解耦模型，并求得解耦變換；其次，利用解耦變換推導建立系統非耦合響應模型，并在微小時段內力源為線性變化的假設下，推導出具體的力源識別公式。最后，采用精細逐步積分方法，對模型進行解算，由結構動態響應反求力源的時間歷程。數值實驗不僅驗證了所提方法可以提高識別精度，而且也驗證了所提方法對非比例阻尼系統也是有效的，這也是文中方法的重點。

Lancaster結構；解耦；精細逐步積分；線性假設

0 引 言

力源識別是根據已知系統的動態特性和實測的動力響應反算結構所受的激勵，是一個較難的問題，但又是結構動態設計的關鍵之一。力源識別問題的研究在各個工程領域都具有重要的意義，如隨著IMO組織對船舶噪聲尤其是艙室噪聲的要求越來越嚴，機電設備作為船舶主要的激勵源，其振動控制越來越受到人們的關注。設備的低噪聲設計是解決設備振動問題的最根本方法，而力源識別又是設備低噪聲設計的前提條件之一。

力源識別方法分為頻域法和時域法。頻域法發展較早，計算方法較為成熟，精度較高。此方法可確定力譜的均值與方差，但對于力的時間歷程還有一定困難，特別是可能會出現奇異值和不穩定現象。而時域識別是20世紀80年代中期發展起來的一種方法，直接依據結構的響應時程來識別未知力源的時間歷程，便于工程應用，受到工程界的歡迎。其中現有的一類力源時域識別方法利用結構的模態模型將系統方程轉化為非耦合形式建立反演模型，具有一定的工程應用價值。

Desanghere等[1]、Ory等[2]于1985年首次將模態坐標變換方法引入到動態力源時域識別過程中，將運動微分方程轉化為非耦合方程形式，將實際載荷的反演轉化為對模態力的反演，在微小時間間隔內力源為階躍力的假設下，推導出已知系統響應等條件下的力源反演公式。唐秀近等[3-4]提出基于模態分解Duhamel積分的一種較為有效的時域載荷識別模式，并較為系統地對該方法的識別精度、模態截斷的影響作了初步的研究。初良成等[5]利用正分析的手法來求解反問題，建立了階躍力假設下的時域載荷識別新方法，克服了識別精度受測量信息數目限制的缺點。徐倩等[6]應用精細逐步積分建立了一種基于階躍力假設下的力源識別模式，由結構動態響應求出動態力的時間歷程。張運良等[7]在微小時段內力源為線性變化的假設下，推導了僅由結構的一種響應（位移、速度或加速度）進行力源識別的遞推連鎖計算公式，以便于實際應用。

這一類力源識別方法無論是階躍力還是線性力假設，在最初都是利用模態坐標變換將系統多自由度微分方程轉化為非耦合形式，然后建立具體的反演公式。但利用坐標變換將三個系數矩陣同時對角化，且僅當比例阻尼或經典阻尼系統才能夠實現，這就使得算法的應用受到了限制。數值代數領域認為，通過主坐標變換來實現三個矩陣的同時對角化一般是無法實現的，因此本文將力源識別中涉及的三矩陣同時對角化轉化為Lancaster擴展系統的塊陣同時對角化，建立系統解耦模型，求得相應解耦變換，并通過理論推導建立系統的非耦合方程表示形式。最后，在微小時間段線性力假設下推導出力源時域識別公式，并利用精細逐步積分進行模型計算。本文數值試驗將涉及無阻尼系統和比例阻尼系統，驗證本文方法較現有基于模態分析載荷識別模型精度高；并將利用兩組船舶運動數據驗證本文提出算法對非比例阻尼系統也適用，且精度較滿意。

1 基于模態分析法的力源識別模型

一個n自由度二階系統往往可由下式來描述：

其中：M、C、K和F分別表示為質量矩陣、阻尼矩陣、剛度矩陣和外力向量。由實測或有限元分析可得系統的模態參數：固有頻率ωr、阻尼比ξr及模態矩陣Φ，其中，利用模態矩陣做變換x（t）=Φq（t），得

左乘矩陣ΦT

若上式為無耦合方程，設Φ= ［Φ1，Φ2，…，Φn］則可寫成分解式

其中：r=1，2，…，n，qr（t）為第r階模態坐標。設（2）式右端項為fr（t），將（2）式降階為一階微分方程

其中：［T（τ）］=eHτ，τ=t-tj，｛vp（t ）｝為方程（3）的特解[5]。利用精細逐步積分法計算指數矩陣 ［T （τ）］[5]，便可得模態坐標qr（t）與外力源F（t）之間的關系式。再由x（t）=Φq（t）推導出結構位移響應x（t）與外力源F（t）的關系，進而實現由結構響應反向推導力源。

顯然，從（1）式到（2）式的轉變意味著主坐標變換x（t）=Φq（t）將三個矩陣M、C、K同時對角化，將多自由度系統簡化為多個單自由度子系統，這個過程也被稱為二階系統解耦[8]。眾所周知，當M和K都為對稱陣，且其中之一為正定陣時，廣義特征值分解可實現M和K的同時對角化，相關的研究方法已經很成熟[8]。三個矩陣的同時對角化不僅要求M、C、K同為對稱陣和某個矩陣為正定陣，還需要滿足KM-1C=CM-1K，但這個條件是很難滿足的，因此工程上涉及到二階系統解耦只能在比例阻尼的假設下實現[8]。

目前數值代數領域利用Lancaster解耦來研究二階系統的解耦問題，將三個矩陣同時對角化轉化為Lancaster擴展系統塊陣同時對角化，已證明幾乎所有二階系統都可以通過這樣的方式實現解耦。文獻[8]詳細地研究和介紹了這一問題，并提出基于Sylvester方程的解耦變換求解方法。本文將利用基于Lancaster結構的二階系統解耦方法建立新的力源識別模型，利用解耦變換通過理論推導建立系統受力相應模型，假設力源在微小時間段內成線性變化的前提下推導力源計算公式。

2 基于系統解耦的力源識別模型建立

2.1 基于Lancaster結構的系統解耦

顯然，當M可逆時（1）式與（4）式對應的特征值問題等價，

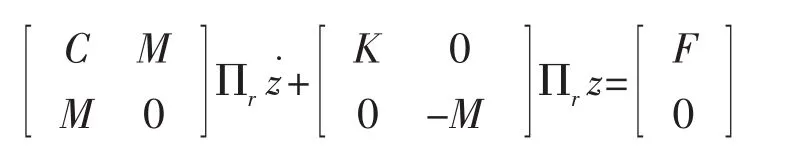
左乘可逆矩陣Πl得

若Πr、Πl可實現（4）式系數矩陣的塊陣同時對角化，便將（4）式轉化為

其中：MD、CD和KD為對角矩陣。顯然，（5）式與（4）式對應的特征值問題等價，若設代入

（6）式即為（1）式所描述原始二階系統的非耦合形式。

2.2 基于精細逐步積分的力源計算

且MDr表示對角陣MD對角線上第r個元素，表示矩陣l11第r行第i列所對應的元素）表示矩陣l21第r行第i列所對應的元素。將（6）式降階為一階微分方程

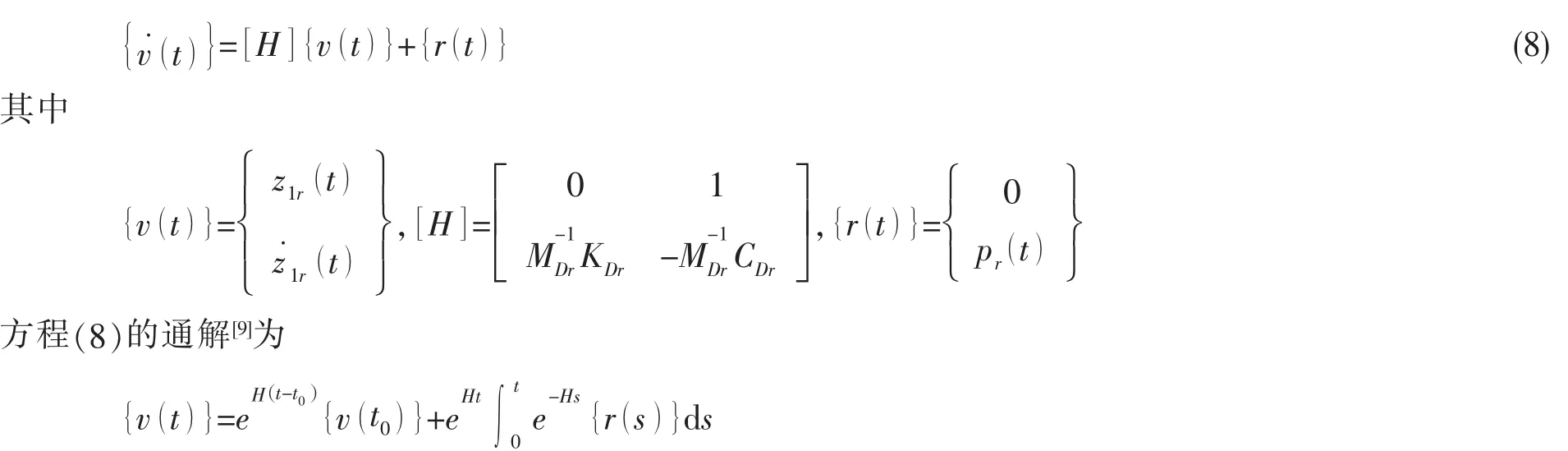
取等間距積分步長τ=tj+1-tj，利用tj時刻的值計算tj+1時刻，令s=tj+ξ，則上式可改寫為

其中：［T （τ）］=eHτ為指數矩陣，利用精細積分方法計算[8-10]。

假設在時間步長 （tj， tj+1）內力r（t）呈線性變化，即

其中：ξ∈ （tj， tj+1），｛r1｝和 ｛r2｝在區間 （tj， tj+1）內為時不變向量，且有

則將（10）式代入（9）式，整理可得線性力源精細積分格式

式中：Tij表示矩陣 ［T （τ）］的第i行第j列，其余類推。

2.3 基于線性力假設的力源識別公式

假設在時間步長 （tj， tj+1）內，力源f（t）是線性變化的，即

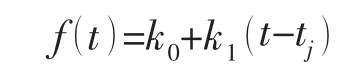
則有

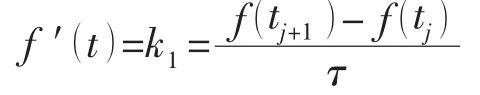
將上式一階導代入（7）式，再將（7）式代入（11）-（12）式，整理得

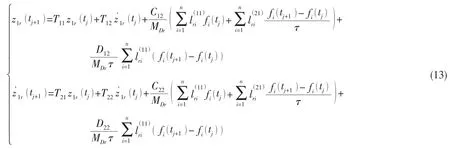
將上式中第2個式子整理得出fi（tj+1）的表達式代入第1個式子，就可以得到fi（ tj）的表達式，從而求解得力源的數值解。

3 算 例

例1針對文獻[6]中涉及的兩自由度無阻尼系統

進行模型仿真計算。首先利用文獻[8]中的方法構造解耦后系統參數矩陣MD和KD，并利用基于Sylvester方程的解耦變換求解方法計算得解耦變換Πr、Πl。然后利用Πr、Πl獲得如（6）式所示的系統非耦合形式。最后在線性力源假設下，取時間步長△t=0.28，利用（13）式計算得力源估計值。表1給出了本文方法與文獻[6]中方法計算的力源估計值，由表中數據可知本文提出的基于系統解耦的力源識別方法精度較高，具體模型計算的絕對誤差如圖1所示。

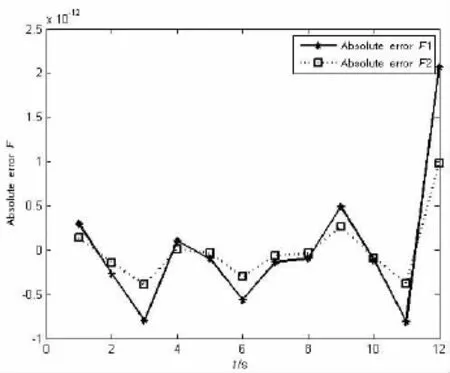
圖1 基于系統解耦力源識別絕對誤差Fig.1 The absolute error of load identification based on decouplingmethod

表1 兩自由度系統力源識別計算結果Tab.1 Calculation result of dynam ic load identification for two DOF system

例2本例將對一船舶振動系統進行力源識別估算，且該力源為動態力，具體系統方程如下：

很顯然，該系統為比例阻尼系統，因此既可以利用模態分析法獲得系統非耦合形式，也可以利用本文方法進行獲得系統解耦形式，下面將給出基于這兩種方法的力源識別模型計算情況。同樣選取時間步長τ=0.02，圖2（a）給出了本文方法計算的力源估計值和真實值曲線，可以看出估計值與真實值基本吻合，圖2（b）則給出了本文方法的誤差曲線；圖2（c）給出了基于模態分析法的力源估計值和真實值曲線，圖2（d）則給出了基于模態分析法的力源估計誤差曲線；從圖2（b）和圖2（d）的幅值比較來看，本文方法精度較高。

圖2 （a） 基于系統解耦力源識別計算值與真值比較曲線Fig.2(a)The comparation between the calculated value and the real value of load identification based on decouplingmethod

圖2 （b） 基于系統解耦力源識別絕對誤差曲線Fig.2(b)The absolute error curve of load identification based on decouplingmethod

圖2 （c） 基于模態法力源識別計算值與真值比較曲線Fig.2(c)The comparation between the calculated value and the real value of load identification based onmodal identification

圖2 （d） 基于模態法力源識別絕對誤差曲線Fig.2(d)The absolute error curve of load identification based onmodal identification

例3本例將對文獻[8]中水池實驗獲得的船舶運動系統數據進行力源識別，所涉及船舶質量為425 t，船長為60m，船舶浪向角為0°，其中共測得18 kns和27 kns航速下各20個遭遇頻率的艦船縱搖—升沉運動數據。

已知船舶運動系統為非比例系統，因此，無法利用模態分析法獲得系統的非耦合方程。利用本文提出的力源識別方法，選取迭代步長τ=0.02進行解算，下面將給出兩組不同航速下不同遭遇頻率下的力源識別結果，圖3和圖4分別給出了計算值與真實值對比圖，以及相應的絕對誤差曲線圖。實驗驗證了此方法對非比例阻尼系統同樣適用。

（1）航速18 kns遭遇頻率Ome=0.889：

（2）數據2：航速27 kns遭遇頻率Ome=0.945：

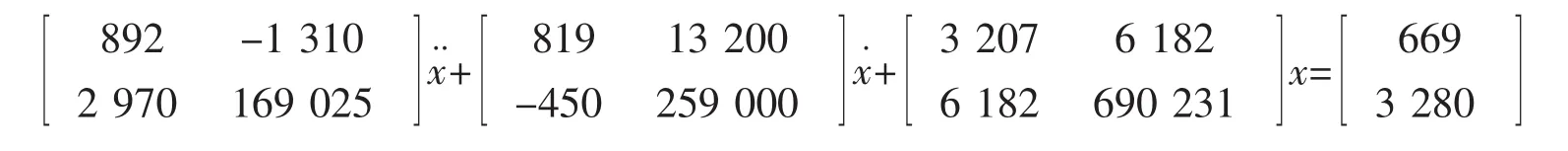
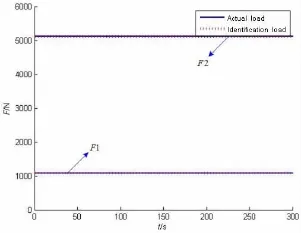
圖3 （a）力源識別計算值與真值對比圖（Ome=0.889）Fig.3(a)The comparation between the calculated value and the real value of load identification(Ome=0.889)

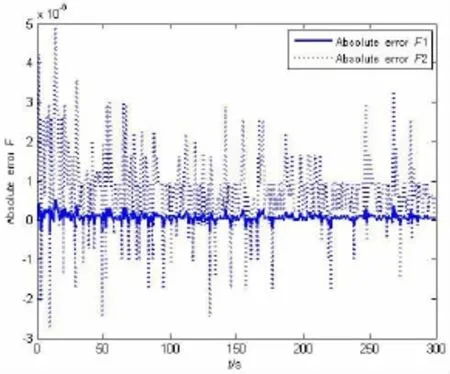
圖3 （b）力源識別絕對誤差曲線圖（Ome=0.889）Fig.3(b)The absolute error curve of load identification(Ome=0.889)

圖4 （a）力源識別計算值與真值對比圖（Ome=0.945） Fig.4(a)The comparation between the calculated value and the real value of load identification(Ome=0.945)

圖4 （b）力源識別絕對誤差曲線圖（Ome=0.945）Fig.4(b)The absolute error curve of load identification(Ome=0.945)

4 結 論

動態載荷的確定在結構的分析與研究中意義重大，準確地識別動態載荷是工程結構可靠性與安全性的重要保證。然而在工程實行中，常常是很難對作用于結構的外載荷作直接測量和計算。因此，對動態載荷的確定只能從可測的系統響應信息來間接地確定。由于其廣泛的工程背景和明顯的應用價值，使這一問題的理論和應用成為研究的熱點。

本文把現有一類載荷時域識別方法涉及到的解耦問題作為切入點，將基于Lancaster結構的二階系統解耦方法應用于系統動力學方程解耦中，并利用解耦變換通過數學理論推導提出了基于系統解耦的載荷識別數學模型，最后采用精細時程積分法進行模型計算。本文提出的模型一方面克服了模態分析法只適用于比例阻尼系統解耦的問題，另一方面從數值試驗來看，針對比例阻尼系統的力源識別精度要高于現有方法，而針對非比例阻尼系統該方法仍然有效。基于Lancaster結構的二階系統解耦方法是數值代數領域的前沿研究之一，一直處于理論研究的階段，因此本文方法也是數學理論研究在工程應用中的一個嘗試。

參 考 文 獻：

[1]Desanghere G,Snoeys R.Indirect identification of excitation foreces bymodal coordinate transformation[C]//Proceedings of the 3rd IMAC.Florida,USA,1985:685-690.

[2]Ory G,Glaser H,Hlzdeppe D.The reconstruction of force function based on aeroelasticity and structural dynamics[M]// Proceedings of 2nd International Symposium On Aeroelasticity and Structural Dynamics.Aschen,FRG,1985:164-168.

[3]唐秀近.動態力識別的時域方法[J].大連工學院學報,1987,26(4):21-27. Tang Xiujin.Dynamic load identification by time domainmethod[J].Journal of DaLian Institute of Technology,1987,26 (4):21-27.

[4]唐秀近.時域動態載荷識別的精度問題[J].大連理工大學學報,1990,30(1):31-37. Tang Xiujin.Precision problems of dynamic load identification in time domain[J].Journal of DaLian University of Technology,1990,30(1):31-37.

[5]Chu Liangcheng,et al.Dynamic load identification in time domain[J].China Ocean Engineering,1990,5(3):279-286.

[6]徐 倩,文祥榮,孫守光.結構動態力源識別的精細逐步積分法[J].計算力學學報,2002,19(1):53-57. Xu Qian,Wen Xiangrong,Sun Shouguang.High precision direct integration scheme for structural dynamic load identification[J].Chinese Journal of ComputationalMechanics,2002,19(1):53-57.

[7]張運良,林 皋,王永學,李志軍,李廣偉.一種改進的動態力源時域識別方法[J].計算力學學報,2004,21(2):209-215. Zhang Yunliang,Lin Gao,Wang Yongxue,Li Zhijun,Li Guangwei.An improved method of dynamic load identification in time domain[J].Chinese Journal of ComputationalMechanics,2004,21(2):209-215.

[8]王淑娟.基于Lancaster結構的二階系統解耦算法研究及其應用[D].哈爾濱:哈爾濱工程大學,2009:1-145. Wang Shujuan.Quadratic system decoupling algorithm researches based on lancaster structure and its applications[D]. Harbin:Harbin Engineering University,2009:1-145.

[9]王 靜,陳海波,王 靖.基于精細積分的沖擊力源時域識別方法研究[J].振動與沖擊,2013,32(20):81-85. Wang Jing,Chen Haibo,Wang Jing.Impulsive load identification in time domain based on precise time-integrationmethod [J].Journal of Vibration and Shock,2013,32(20):81-85.

[10]鐘萬勰.結構動力方程的精細時程積分法[J].大連理工大學報,1994,32(2):131-136. ZhongWanxie.On precise time-integrationmethod for structural dynamics[J].Journal of DaLian University of Technology,1994,32(2):131-136.

[11]林家浩,沈為平,威廉斯FW.受演變隨機激勵結構響應的精細逐步積分法[J].大連理工大學學報,1995,35(5): 600-605. Lin Jiahao,Shen Weiping.High precision direct integration scheme for analysing structural nonstationary random responses[J].Journal of DaLian University of Technology,1995,35(5):600-605.

[12]鐘萬勰,楊再石.連續時間LQ控制主要本征對的算法[J].應用數學和力學,1991,12(1):45-50. Zhong Wanxie,Yang Zaishi.On the computation of themain eigen-pairs of the continuous-time linear quadratic control problem[J].Applied Mathematics and Mechanics,1991,12(1):45-50.

A load identification method based on decoup ling of Lancaster structure

WANG Shu-juan,WANG Guo-qiao,SHEN Ji-hong,HANWei-min
(School of Science,Harbin Engineering University,Harbin 150001,China)

The way of the load identification in time domain which is based on themodal analysis that the system equation is transformed into a non-coupling form bymodalmatrix,is only applicable for the proportional damping or classical damping system.In this paper,based on structure-preserving decoupling method of second-order system,a new mathematicalmodel of load identification was established.The system-decouplingmodel was established based on the Lancaster structure and the decoupling transformation was obtained;then,themodel of uncoupled response system based on the decoupling transformation was established,and on the assumption of linear load identification in tiny-time,the formula of load identification was deduced;finally,themodelwas calculated based on high precision direct integration scheme, and the history of force identification was obtained by structural dynamic response.The experiments verify that the proposed method could improve the accuracy of recognition,and is effective for the non-proportional damping system.And it is the focus of the paper.

Lancaster structure;decoupling;high precision direct integration scheme;linear assumption

TB535

：Adoi:10.3969/j.issn.1007-7294.2017.01.007

2016-09-09

國家自然科學基金資助項目（11226324）；黑龍江省基金資助項目（A201407）

王淑娟（1982-），女，碩士生導師，E-mail：wangshujuan@hrbeu.edu.cn；

王國巧（1990-），女，碩士研究生，E-mail：Wgq19900424@163.com；

沈繼紅（1966-），男，教授，博士生導師；

韓偉民（1990-）；男，碩士研究生。

1007-7294（2017）01-0052-09