對稱Alpha穩定分布噪聲下的Duffing振子檢測方法

李 楠，李秀坤，劉彩虹

（1.哈爾濱工程大學 a.水聲技術重點實驗室；b.水聲工程學院，哈爾濱 150001；2.東北電力大學 信息工程學院，吉林132012）

對稱Alpha穩定分布噪聲下的Duffing振子檢測方法

李 楠1a，b，2，李秀坤1a，b，劉彩虹1a，b

（1.哈爾濱工程大學 a.水聲技術重點實驗室；b.水聲工程學院，哈爾濱 150001；2.東北電力大學 信息工程學院，吉林132012）

Duffing振子是利用系統對與策動力同頻的小信號敏感而對噪聲免疫實現微弱信號檢測，特定分布下的噪聲激勵Duffing振子系統不會發生相變是應用該方法的前提條件。文中主要研究了服從Alpha穩定分布的噪聲激勵Duffing振子產生相變的魯棒性問題，研究結果表明Duffing振子相變在Alpha穩定分布源的激勵下為小概率事件。為消除小概率相變的影響，利用多支路并行檢測及多數判決準則對常規的Duffing振子檢測方法進行改進，即將待測信號分段截短周期延拓后送入多個并行Duffing振子檢測單元，若檢測單元多數發生相變，必然是由于弱目標信號而非噪聲激勵所致，即可判定檢測信號中包含目標小信號。將該方法應用于水下目標回波信號的檢測中，實測數據處理結果驗證了該方法是有效的。

Duffing振子；對稱Alpha穩定分布；小概率事件；多支路并行檢測

Key words:Duffing oscillator;symmetricα-stable distribution;small probability event; multi-branch parallel detection

0 引 言

強背景噪聲下的弱信號檢測一直是故障診斷、通信、雷達、聲納及生物醫學等領域研究的熱點問題，傳統信號處理方法對這類信號的檢測能力有限，非線性動力學的發展為強噪聲背景下的微弱信號檢測開辟了一條新的途徑。基于Holmes的Duffing振子的微弱信號檢測一直是國內外學者研究熱點問題，研究方向之一是對Duffing振子隨機共振現象的研究，即在特定系統參數下非線性系統、弱信號與噪聲三者產生協同作用，一部分噪聲能量轉移到信號身上使系統發生隨機共振現象從而實現弱信號檢測。Duffing振子的隨機共振研究始于1989年[1]，隨后，國內學者康艷梅首先基于絕熱近似理論研究了弱噪聲極限下受小幅低頻周期力驅動的二維布朗運動的隨機共振現象，得出了一些有意義的結論[2]。韓祥臨等[3]利用泛函廣義變分迭代原理得到了廣義Duffing擾動振子隨機共振機理的近似解。冷永剛等[4]以Kramers逃逸速率為基礎，建立了Duffing振子隨機共振的判別函數，闡述了Duffing振子在不同噪聲強度及信號頻率輸入條件下的廣義調參隨機共振規律。趙志宏等[5]研究了Duffing系統噪聲強度與信噪比及不同頻率正弦信號與信噪比的關系，分析了阻尼比參數對隨機共振的影響。上述研究取得的成果均是基于理論推導或在數值仿真層面上實現，應用于實際還存在一定困難，這是因為隨機共振現象是在某一噪聲強度下達到最佳輸出，隨著噪聲強度的減弱或增強系統的共振現象逐漸變弱。通常實測信號中的噪聲強度是未知的，并且可能是隨機變化的，通過調節噪聲強度誘導隨機共振比較困難。另一研究方向是利用Duffing振子對參數及初始值的敏感性實現微弱信號檢測。自1992年Birx[6]首次提出了應用Duffing混沌系統檢測微弱信號以來，國內外眾多學者對Duffing系統混沌機理進行分析，將研究重點放在如何從較低信噪比中檢測出微弱的周期信號[7-9]。李月等[10]通過對Duffmg方程中的非線性項進行修正，提出了色噪聲背景下檢測微弱信號的新模型，檢測信噪比下限達到-111.46 dB，且對高斯色噪聲下畸變正弦信號也有一定的檢測能力。李月和吳等[11-12]改進了單個Duffing振子檢測模型，提出采用雙耦合及環形耦合振子實現微弱信號檢測，進一步提高了檢測性能及抗噪性能。上述研究成果均是在高斯分布的白噪聲或色噪聲下得出的，然而真實世界的噪聲如音頻信號、水下聲納采集的信號、雷達和衛星通信接收信號中的噪聲常常是非高斯的、并伴有顯著的脈沖特性[13]。研究特定分布噪聲下的Duffing振子系統特性對實際工程應用具有重要意義。

傳統信號處理方法通常將背景噪聲假設為滿足中心極限定理的高斯分布，但有研究成果表明，對稱Alpha穩定分布是符合自然噪聲產生機制和傳播條件的極限分布，能更準確地描述真實噪聲的物理模型[14-16]。利用Duffing振子對該類背景噪聲下的信號檢測時必然遇到一個基礎性的問題，即服從對稱Alpha穩定分布的源信號激勵Duffing振子時系統是否會發生相變及相變的程度如何。本文重點研究了服從對稱Alpha穩定分布噪聲單獨作用于Duffing振子時系統相態的變化情況，在此基礎上改進了常規Duffing振子檢測方法，將多支路并行檢測與多數判決結合實現微弱信號檢測。該方法對接收數據進行分段截短及周期延拓預處理，將重構的序列矩陣送入Duffing振子陣列進行多支路并行檢測，綜合各支路基本單元的輸出結果采用多數判決準則進行檢測，從而降低了檢測虛警概率。本文在水下干擾信號特性服從對稱Alpha穩定分布情況下，將多支路并行檢測Dufifng振子方法應用于水下目標弱信號檢測，驗證了該方法的可行性及有效性。

1 Alpha穩定分布理論

1.1 Alpha穩定分布統計描述

Alpha穩定分布最初由Lévy在1925年研究廣義中心極限定理時提出，它是唯一滿足廣義中心極限定理的分布，很多不滿足經典的中心極限定理的數據都可用穩定分布來描述，是高斯分布的推廣分布形式。Alpha穩定分布的概率密度函數存在且連續（除了某些特殊參數外概率密度函數沒有統一封閉形式），因此，通常采用特征函數來描述。

Alpha穩定分布的特征函數為：

（1）式中參數含義如下：

① 參數α∈（0，2]稱為特征指數，決定該分布脈沖特性的程度，當α=2時，分布即為高斯分布。α值越小，所對應分布的拖尾越厚，脈沖特性越顯著。

② 參數γ≥0為分散系數，是相對于均值的分散程度，類似于高斯分布中的方差。

③ 參數a為位置參數，若1＜α≤2，則a表示均值，若0＜α≤1，則a表示中值。

④ 參數-1＜β＜1稱為對稱參數，用于確定分布的斜度。

若滿足β=a=0時，該分布為對稱Alpha穩定（Symmetricα-stable，SαS）分布，其特征函數為下式所示：

不同α參數下對稱α穩定分布的概率密度函數如圖1所示，由圖中可以看出α越小，分布拖尾越厚，表明偏離中心值的樣本越多。α=1，β=0時，穩定分布與柯西分布一致；α=2時，穩定分布與高斯分布一致。

1.2 對稱α穩定分布的參數估計

(2)首先，自動機A接受安全屬性的否定,也就是接受的是壞前綴，所以M中的接收狀態集F′是系統的不安全狀態.其次，在M構造過程中刪除了從初始狀態不可達狀態以及與監控屬性無關的狀態，而這些狀態相對于φsafe來說是安全狀態，因此t時刻系統安全性的概率Prt(M

由于對稱Alpha穩定分布的概率密度函數不存在清晰明確的表達式，傳統依賴于顯式的概率密度函數數學統計方法不再適用，因此人們可以采用數值計算的方法估計穩定分布的參數。常用方法有最大似然估計法、基于樣本分位數參數估計法、基于樣本特征函數的參數估計方法及基于負階矩方法。在對實測信號分析處理時，通常信號的先驗知識未知，常采用基于負階矩方法中的方法進行參數估計[17]。

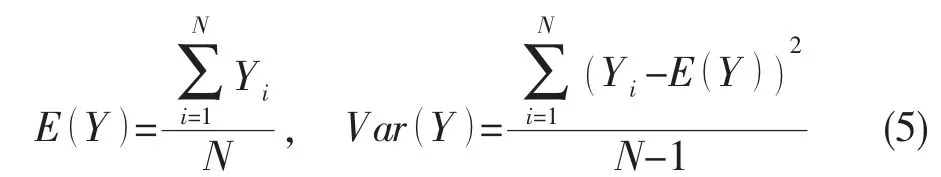
其中：N是樣本總數，Yi是獨立同分布的觀測值，則α和γ可由（6）式和（7）式估計得到：

其中：Ce=0.577 215 66…是Euler常數。

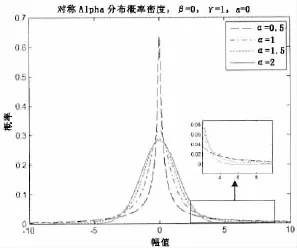
圖1 不同α值時對稱α穩態分布概率密度函數Fig.1 The probability density function of a symmetric α-stable distribution for differentαvalue

對稱Alpha穩定分布的對稱參數限定為β=0；位置參數a可根據α估計值確定，當α＞1時，樣本均值是位置參數a的一致估計，1≥α＞0，樣本中值是位置參數a的一致估計。

2 對稱Alpha穩定分布噪聲下Duffing振子性能分析

2.1 對稱Alpha穩定分布噪聲激勵下Duffing振子相變魯棒性分析

目前，已有的研究成果主要針對Duffing振子在高斯分布的白噪聲及色噪聲背景下微弱信號的檢測能力進行了深入研究，研究指出在統計意義下零均值的白噪聲及色噪聲都不會改變系統原有運行軌跡。Duffing振子對服從對稱Alpha穩定分布噪聲的免疫力如何，即對稱Alpha穩定分布噪聲激勵Duffing振子是否會發生相變，是利用Duffing振子實現微弱目標信號檢測的前提與基礎。

檢測系統采用Duffing-Holmes方程：

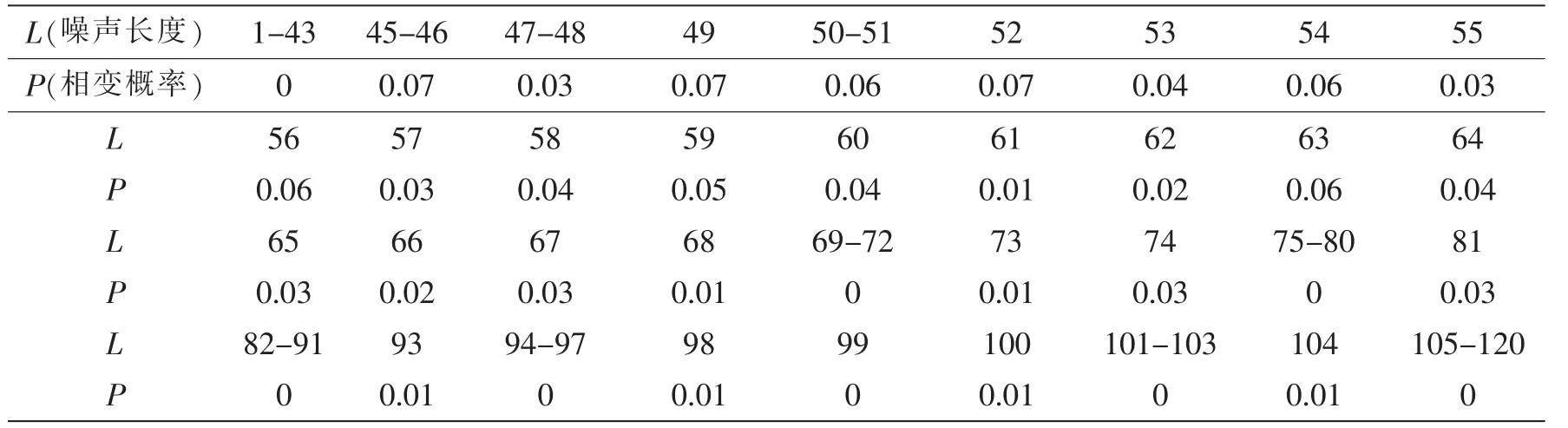
表1 L不同的噪聲序列激勵Duffing振子系統發生相變的概率Tab.1 The probability of phase-state transition when the Duffing oscillator system is excited by the truncated noise of different length

從表1及圖2可得出如下結論：

（1）噪聲序列長度在L＜45&L≥105時，Duffing振子系統發生相變概率為零，系統相態穩定，不會引起系統相變導致誤判，這一穩定的表現可用于識別微弱信號是否存在。在實際處理過程中，可視實際需要選取數據長度；

（2）噪聲序列長度在45≤L≤104范圍內時，出現小概率的Duffing振子相態變化。在分析過程中發現：即使序列長度L相同，引起混沌相態變化也比較復雜，系統相態呈現混沌態、過渡過程周期態、混沌/大尺度臨界態、大尺度周期態等多種相態表現形式，表明系統相變具有一定的隨機性。由圖2可知，在噪聲的激勵下Duffing振子系統由混沌轉變為大尺度最大概率為0.07，且出現次數百分比僅為3.3%，出現概率小，次數少，基本可認為是小概率事件。在實際檢測過程中，可增加檢測判決次數，采取多數判決準則降低誤判概率；

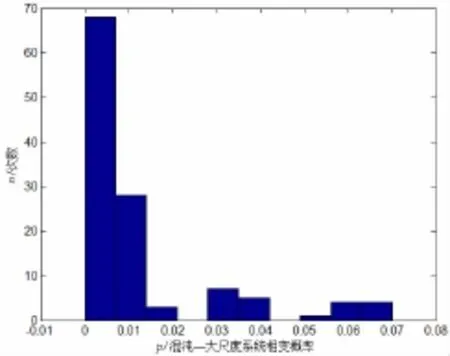
圖2 混沌系統相變概率直方圖Fig.2 The probability histogram of the phase-state of chaotic system

（3）噪聲序列長度L≥120時，Duffing振子系統出現相變概率基本為零，由于表中篇幅有限省略并未列出。

2.2 Duffing振子對噪聲強度的檢測能力分析

在高斯噪聲條件下，通常采用對數噪聲信號功率比定義信噪比（SNR-signal to noise ratio）。但符合SαS分布的隨機噪聲，由于不存在有限的二階矩，致使其方差變得沒有意義。因此，需要對信噪比定義進行修正如下：

其中：S表示待檢信號平均功率，γv為對稱α穩定分布噪聲的分散系數。當α=2時，對稱Alpha穩態分布退化為高斯分布，則為高斯分布方差

根據（10）式定義，通過在對稱Alpha穩定分布的噪聲中改變加入的周期信號幅值調整信噪比，周期信號頻率f=0.06 kHz，討論噪聲強度對Duffing振子弱信號檢測能力的影響。大量仿真結果表明，可檢測信號的最低信噪比為SNR=-16.302 9 dB，仿真結果見圖3。

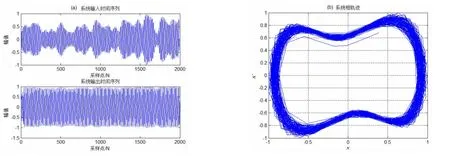
圖3 （a）Duffing振子輸入信號、輸出信號時域信號波形圖；（b）Duffing振子系統相圖Fig.3(a)Input signal and output signalwaveform of Duffing oscillator in time domain;(b)The phase-state diagram of Duffing oscillator

3 多支路并行Duffing振子檢測方法

基于1，2章的理論分析及仿真研究，對常規Duffing振子檢測方法進行改進。改進方法將多個Duffing振子構成并行檢測陣列，調整參數使每個振子處于混沌/大尺度臨界狀態；接收信號經帶通濾波、分段截取及周期延拓后重構為M×N維時間序列矩陣（M取奇數便于多數判決），將M路序列送入并行的基本單元檢測，若陣列中多數Duffing振子發生相變，由于對稱Alpha穩定分布噪聲引起系統相變為小概率事件，則多數Duffing振子相變必定是由待檢信號中含有與策動力同頻弱周期信號激勵所致。并行檢測多數判決消除了小概率事件影響，提高了檢測準確率。其檢測流程框圖見圖4所示。

基本檢測單元由周期延拓、Duffing振子微分方程龍格—庫塔法求解和相軌跡判決三部分構成。在實際檢測過程中，存在由于待檢時間序列中所包含周期信號的周期數較少不足以激勵Duffing系統發生相變而產生誤判的情況。本文給出的解決方案是對待檢信號時間序列分段截短周期延拓構建新的子波序列作為Duffing振子檢測系統的信源，周期延拓示意圖見圖5，T1=T2=…Ti=…=TM為待測信號的周期，i=1，2…M為支路下標，N為周期延拓倍數，通常N不小于15。

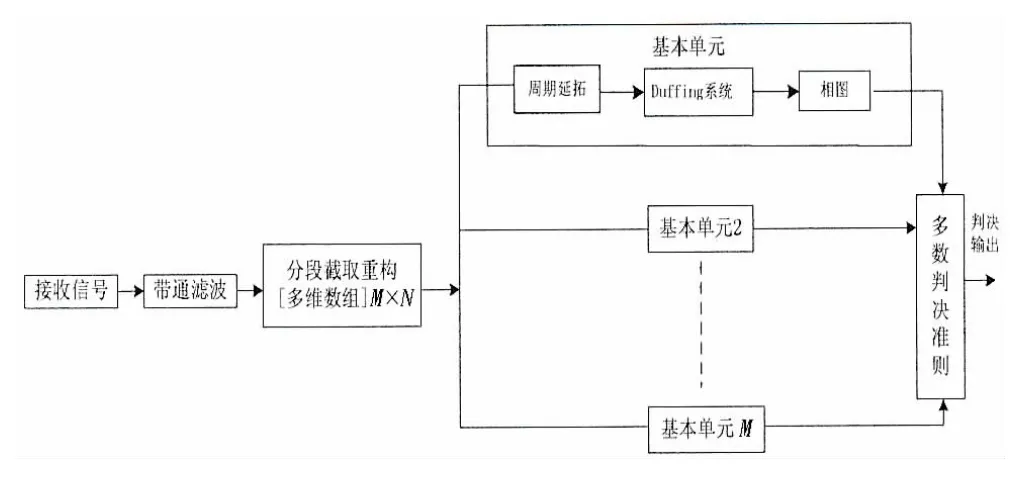
圖4 Duffing振子檢測流程圖Fig.4 Detection principle diagram of Duffing oscillator

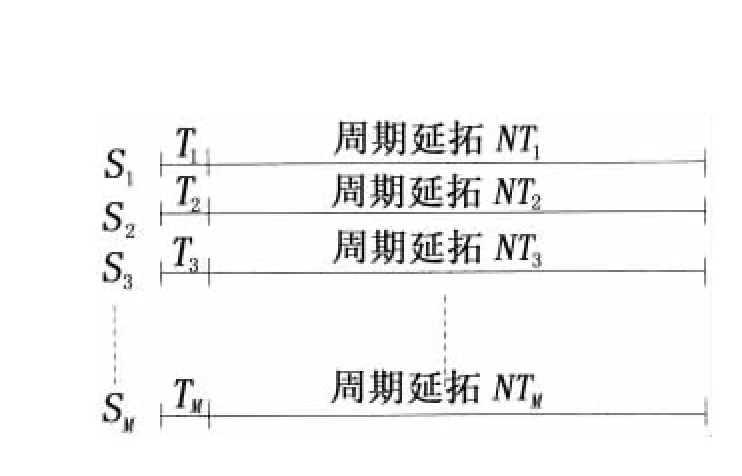
圖5 分段周期延拓示意圖Fig.5 Diagram of periodic extension

系統輸出采用多數判決準則可降低目標判決時的虛警概率，若采用單支路Duffing振子檢測時系統的誤判率為p，根據多數判決準則多支路的誤判率為：

其中：c為Duffing振子支路總數，r為進行多數判決準則的判決支路下限。

4 實驗仿真

采集某水域水下噪聲及目標回波數據，驗證多支路并行Duffing振子方法的檢測效果，首先需對水下噪聲的SαS特性進行檢驗（數據分析及實驗結果只對本次采集的樣本數據有效）。

4.1 水下噪聲特性

在未放置水下目標時接收裝置接收的數據為水下噪聲，圖6為某一組水下噪聲樣本的采樣時序波形圖。選取四組數據樣本統計分析水下噪聲的瞬時值概率密度分布pi（f，τ ）見圖7，橫軸為歸一化幅值。由圖7可知，水下噪聲的瞬時值概率分布具有“中心對稱性”，用高階統計量偏斜度Sk和峭度Ku至少有一個不恒為零及樣本方差是否收斂檢驗數據穩定分布的高斯性，四組實測樣本數據的偏斜度和峭度統計值見表2所示，樣本方差見圖8。

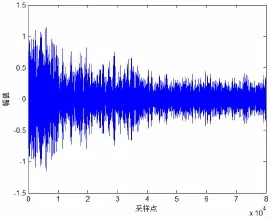
圖6 背景噪聲時域波形圖Fig.6 Time-domain waveform of the background noise

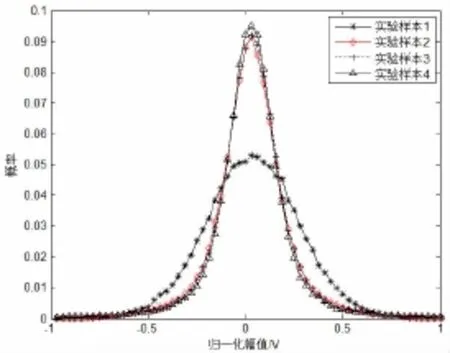
圖7 噪聲瞬時值概率密度分布Fig.7 Probability density distribution of background noise

表2 水下噪聲偏斜度及峭度統計值Tab.2 The skewness and kurtosis of underwater noise

由表2可知，實測樣本數據的偏斜度值Sk近似趨于零，峭度值Ku均為大于零的正數，圖8中實測數據的樣本方差在小樣本情況下隨機變化呈現區間震蕩形態并不收斂于某一有限值。因此，可判定水下噪聲具有非高斯分布。水下噪聲分布特性是否符合對稱Alpha穩定分布，可將實測樣本數據與基于SαS模型（參數α=1.673 5，γ=0.15）生成數據的瞬時值概率密度進行匹配分析，圖9為兩者瞬時值概率密度。從圖9可以看出，水下噪聲的瞬時值分布以較高的精度滿足對稱Alpha穩定分布形式。

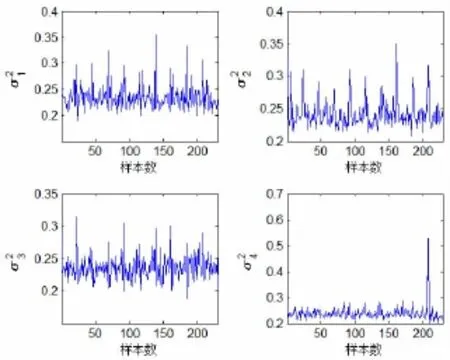
圖8 水下噪聲實測樣本隨樣本數變化曲線Fig.8curveswith sample number of underwater noise

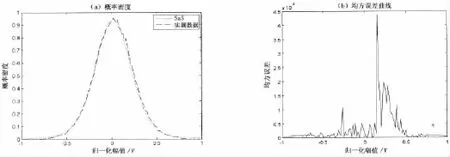
圖9 瞬時值概率密度分布匹配分析Fig.9(a)Probability density distribution of instantaneous valuematching analysis;(b)mean square error curve

4.2 水下目標的多支路并行Duffing振子檢測法

采用本文提出的多支路并行Duffing振子檢測方法對水下回波信號進行檢測，設置Duffing振子陣列數M=5，對采集樣本數據分段截取10個發射信號周期的數據點數進行周期延拓后送入Duffing檢測基本單元陣列，各路基本檢測單元輸入及輸出時間序列波形及系統相圖見圖10。由圖10可知，系統輸入時間序分段截短后經周期拓延，將其送入檢測陣列，當發生由混沌態向大尺度周期態相變時系統輸出時間序列波形為穩定的周期序列。由系統相圖可看出，圖10（a）、（d）系統相軌跡經短暫過渡狀態進入大尺度周期態，圖10（b）、（c）系統相軌跡直接進入大尺度周期態；圖10（e）系統相軌跡顯現間歇混沌態。根據多數判決準則，結合輸出時域波形及系統相軌跡結果，5條支路中有4條支路出現由混沌態向大尺度周期態的相變，即可認為待檢測信號中存在弱CW目標回波信號。

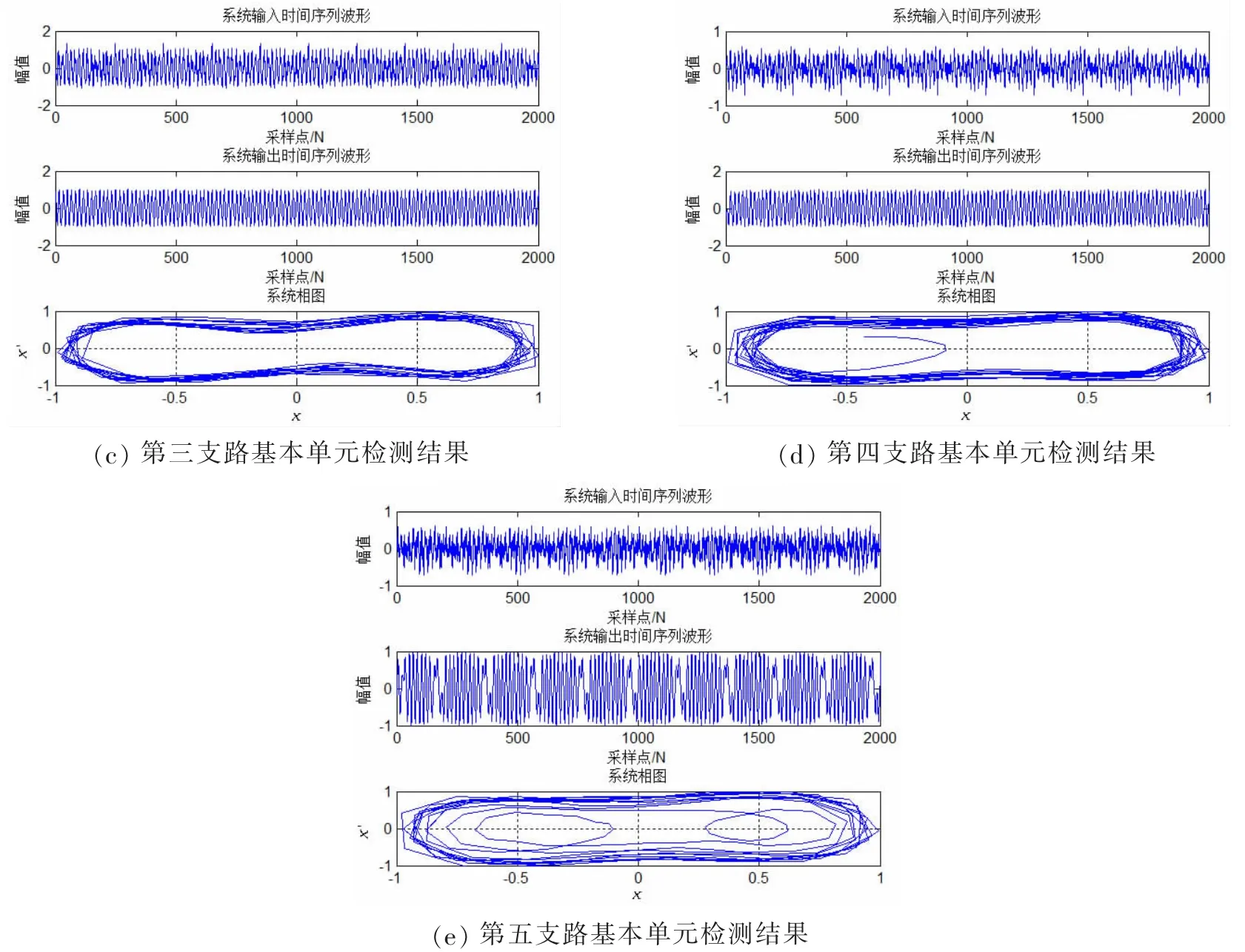
圖10 實驗Duffing振子系統相圖Fig.10 The phase-state diagram of the Duffing oscillator in the lake experiment

5 結 論

本文以對稱Alpha穩定分布的噪聲下Duffing振子的微弱信號檢測能力為出發點，研究了對稱Alpha穩定分布的噪聲激勵Duffing振子發生相變的魯棒性問題，研究發現服從對稱Alpha穩定分布的噪聲激勵Duffing振子系統發生相變為小概率事件，Duffing振子對其具有一定的免疫力，該結論為實現對稱Alpha穩定分布的噪聲下的弱信號檢測提供了依據。為消除對稱Alpha穩定分布的噪聲激勵下Duffing系統的小概率相變因素，改進了常規的Duffing振子檢測方法，將待檢測數據進行分段截取進行周期延拓，之后送入多個并行Duffing振子基本單元進行檢測，綜合多個檢測單元結果采用多數判決準則給出檢測結果。根據服從對稱Alpha穩態分布的變量不存在二階矩對信噪比進行了修正，數值仿真實現了信噪比為-16 dB的目標信號檢測。同時，湖試實驗數據檢測結果驗證了多支路并行檢測Duffing振子方法的可行性及有效性。

[1]Gammaitoni L,Marchesoni F,Menichella-Saetta E,Santucci S.Stochastic resonance in bistable systems[J].Phys Rev Lett,1989,62:349-352.

[2]康艷梅,徐健學,謝 勇.弱噪聲極限下二維布朗運動的隨機共振現象[J].物理學報,2003,52(4):802-808. Kang Yanmei,Xu Jianxue,Xie Yong.Stochastic resonance in two-dimensional Brownian motion in the weak noise[J]. Acta physic Sinica,2003,52(4):802-808.

[3]韓祥臨,林萬濤,許永紅,等.廣義Duffing擾動振子隨機共振機理的漸近解[J].物理學報,2014,63(17):35-39. Han Xianglin,Lin Wantao,Xu Yonghong,et al.Asymptotic solution to the generalized Duffing equation for disturbed oscillator in stochastic resonance[J].Acta Physic Sinica,2014,63(17):35-39.

[4]冷永剛,賴志慧.基于Kramers逃逸速率的Duffing振子廣義調參隨機共振研究[J].物理學報,2014,63(2):020502. Leng Yonggang,Lai Zhihui.Generalized parameter-adjusted stochastic resonance of Duffing oscillator based on Kramers rate[J].Acta Physic Sinica,2014,63(2):020502.

[5]趙志宏,楊紹普,劉永強.基于Duffing振子的隨機共振研究[J].動力學與控制學報,2014,12(2):160-164. Zhao Zhihong,Yang Shaopu,Liu Yongqiang.Study of stochastic resonance based on duffing oscillator[J].Journal of Dynamic and Control,2014,12(2):160-164.

[6]Birx D L.Chaotic oscillators and CMFFNS for signal detect in noise environment[J].IEEE International Joint Conference on Neural Network,1992,2:881-888.

[7]Wang Guanyu,Chen Dajun.The application of oscillators to weak signal detection[J].IEEE Transaction on Industrial Electronics,1999,46(2):440-444.

[8]王冠宇,陶國良,陳 行,等.混沌振子在強噪聲背景信號檢測中的應用[J].儀器儀表學報,1997,18(2):209-212. Wang Guanyu,Tao Guoliang,Chen Xing.The application of the oscillator in the strong background noise[J].Chinese Journal of Scientific Instrument,1997,18(2):209-212.

[9]聶春燕,石要武.基于互相關檢測和混沌理論的弱信號檢測方法研究[J].儀器儀表學報,2001,22(1):37-32. Nie Chunyan,Shi Yaowu.The research of weak signal detection based on cross-correlation and chaos theory[J].Journal of Instrumentand Meter,2001,22(1):37-32.

[10]李 月,楊寶俊,石要武.色噪聲背景下微弱正弦信號的混沌檢測[J].物理學報,2003,52(3):526-530. Li Yue,Yang Baojun,Shi Yaowu.Chaos-based weak sinusoidal signal detection under colored noise background[J].Acta Physic Sinica,2003,52(3):526-530.

[11]李 月,路 鵬,楊寶俊,等.用一類特定的雙耦合 Duffing振子系統檢測強色噪聲背景中的周期信號[J].物理學報, 2006,55(4):1672-1677. Li Yue,Lu Peng,Yang Baojun.Applying a special kind of two coupled Duffing oscillator system to detect periodic signals under the background of strong colored noise[J].Acta Physic Sinica,2006,55(4):1672-1677.

[12]吳勇峰,張世平,孫金瑋,等.環形耦合Duffing振子間的同步突變[J].物理學報,2011,60(2):145-150. Wu Yongfeng,Zhang Shiping,Sun Jinwei,et al.Abrupt change of synchronization of ring coupled Duffing oscillator[J]. Acta Phys.Sin.,2011,60(2):145-150.

[13]唐 洪,邱天爽,李 婷.非高斯alpha穩定分布環境中自適應濾波及研究進展[J].系統工程與電子技術,2005,27 (8):1336-1341. Tang Hong,Qiu Tianshuang,Li Ting.Development of adaptive filtering algorithms in non-Gaussian alpha-stable environment[J].Systems Engineering and Electronics,2005,27(8):1336-1341.

[14]劉 嘩,黃芝平,劉純武.Alpha穩定分布混響建模及信號檢測[J].國防科技大學學報,2012,34(4):148-163. Liu Ye,Huang Zhiping,Liu Chunwu.Reverberationmodeling and signal detection based on Alpha stable distribution[J]. Journal of National University of Defence Technology,2012,34(4):148-163.

[15]Georgiou PG,Tsakalides P,Kyriakakis C.Alpha-stablemodeling of noise and robust time-delay estimation in the presence of impulsive noise[J].IEEE Transactions on Multimedia,1999,1(3):290-301.

[16]Tsihrintzis G A,Nikias C L.Fast estimation of the parameters of Alpha-stable impulsive interference[J].IEEE Transaction on Signal Processing,1996,44(6):1492-1503.

[17]邱天爽,張旭秀,李小兵,等.統計信號處理—非高斯信號處理及其應用[M].北京:電子工業出版社,2004. Qiu Tianshuang,Zhang Xuxiu,Li Xiaobing,etal.Statistical signal processing-Non-gauss signal processing and its applications[M].Beijing:Publishing House of Electronics Industry,2004:140.(in Chinese)

Detection method of the Duffing oscillator under symmetric Alpha-stable noise

LINan1a,b,2,LIXiu-kun1a,b,LIU Cai-hong1a,b
(1a.Acoustic Science and Technology Laboratory;b.College of Underwater Acoustic Engineering,Harbin Engineering University, Harbin 150001,China;2.College of information Engineering,Northeast DianliUniversity,Jilin 132012,China)

Duffing oscillator own the property of sensitivity to small signal and immune to noise,which can be used to detectweak signal.The precondition of applying thismethod is that the phasemotion of the system does not transit by excitation of the noise under the specific distribution.Duffing oscillator subjected to excitation by noise under symmetric Alpha-stable distribution,the robustness of the phase-state transition is studied.The simulation results show that the phase-state transition of the system is a small probability event.In order to eliminate the effect of small probability event,amulti-branch parallel detection method of the Duffing oscillator is proposed.Themeasured signal is truncated and periodic extended,then processed signals are sent tomulti-branch parallel detection units.If phase state of themost branches transit in large periodic state,it is due to the excitation of small target signal rather than the noise.Namely,the detected signal contains the target signal.The proposedmethod is applied to the detection of underwater target echo signals,and the results show that thismethod is effective.

U661.1

：Adoi:10.3969/j.issn.1007-7294.2017.01.011

2016-11-24

國家自然科學基金資助項目（51279033）；黑龍江省自然科學基金資助項目（F201346）

李 楠（1973-），女，副教授，E-mail：jllinan@163.com；

李秀坤（1962-），女，教授。

1007-7294（2017）01-0090-09