數學史對職前教師教學知識影響的質性研究
——以無理數的教學為例

黃友初

（南京師范大學 課程與教學研究所，江蘇 南京 210097）

數學史對職前教師教學知識影響的質性研究
——以無理數的教學為例

黃友初

（南京師范大學 課程與教學研究所，江蘇 南京 210097）

教學知識是教師特有的專業知識，對教師的教學有著重要的影響．以無理數的教學為例，研究數學史對職前教師教學知識的影響．研究發現，數學史能提升職前教師的無理數教學知識．在學科內容知識方面，數學史能幫助職前教師了解無理數和其它知識點之間的聯系，了解無理數及其名稱的由來．而數學史對職前教師教學內容知識的影響更大，能幫助職前教師更準確地判斷學生的思維過程，更好地把握教學的重難點，使得教學設計變得更加合理．

數學史；教學知識；無理數

1 研究背景

教師是一項專業性較強的職業，教師有效教學所需要的知識是教師的專業知識，可稱為教師教學知識或者教師知識，它有別于一般的學科知識，是教師職業專業化的必備特質．以數學為例，一般學過數學的人只要能理解并運用相關的數學知識即可，但作為數學教師除了需要掌握這些學科知識以外，還需要了解并掌握該知識點的重點和難點是什么，學生最容易出現哪些錯誤，該怎么教最適合學生的學習，知識點與學生已掌握的知識之間有怎樣的聯系，該知識點需要講到什么深度即可，等等，這些都屬于教師教學知識的范疇．知識是個體的核心特質，教師的教學知識直接影響著教師的教學行為，提升教師的教學知識，對促進教育的發展有著重要的價值．那么，哪些因素會影響教師的教學知識？教師教育中數學史課程的學習對教師的教學知識有著怎樣的影響？這些問題目前還缺乏深入研究，這里將以無理數的教學為例，探索數學史對職前教師教學知識的影響．

2 理論基礎

在20世紀初期，就有學者關注教師的知識結構和知識深度對教師教學的影響，并開始探討教師的有效教學都需要具備哪些知識[1]．在早期，學者們都意識到教師所具備的學科知識對教師的教學會產生直接的影響．有學者研究表明，教師的學科知識與學生的學業成就在一定程度內（例如幾門課程內）具有正相關性[2]；也有學者研究表明，教師的學科知識越多，教學越有效，與其它知識的聯結也越多[3]．但是，學科知識并不等價于教學知識，并不意味著教師掌握的學科知識越高深，教學效果就一定會越好，這點從很多一流數學家在數學教學方面并不擅長就可以看出．在對教師教學所需要的知識進行深入探索后，學者們發現除了學科知識影響教師的教學以外，有關教學方法的知識也會影響教師的教學，并在教學中扮演著重要的角色．甚至有學者認為，怎么教比教什么更為重要[4]；也有學者認為有關教學方法的知識是教師教學知識的核心[5]．在美國學者Shulman提出PCK的概念以后，人們逐漸開始從學科知識和教學方法的知識兩個方面對教師知識進行了研究，也提出了很多種教學知識的結構模型．其中美國學者Ball所提出的MKT模型，近年來受到學者們的廣泛關注．該模型基于扎根理論，將教師教學知識分為學科內容知識（SMK）和教學內容知識（PCK）兩個部分．其中學科內容知識又分為一般內容知識（CCK）、專門內容知識（SCK）、水平內容知識（HCK）3個方面；教學內容知識分為內容與學生的知識（KCS）、內容與教學的知識（KCT）、內容與課程的知識（KCC）3個部分[6]，具體如圖1所示．由于該模型和教師教學的特點比較吻合，能從“教什么”和“怎么教”兩個方面闡述教師有效教學所需要的知識結構，在教學知識的研究中得到較為廣泛的運用．研究將以MKT模型為依據，分析教師教學知識的變化情況．

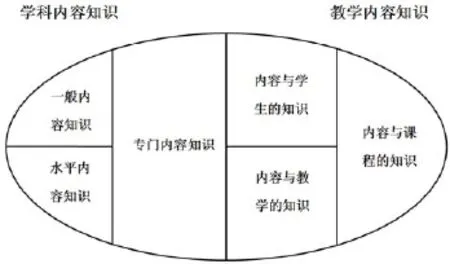
圖1 MKT結構圖

數學史對數學教育的影響已有較多的研究，也有很多學者探討了數學史對數學教師的影響[7]，數學史對學生數學學習的影響[8]，以及數學史融入數學教學的各種策略[9]．但是從教學知識的視角，探討數學史對數學教師教學影響的研究還不多．鑒于教學知識的重要性和數學史的教育性，有必要對數學史和教師教學知識的聯系進行研究分析．

在無理數的教學中，如何讓學生更好地認識和接受無理數，是教師在教學中面臨的困難之一．之所以會出現這種現象，有其必然性．因為在學習無理數以前，學生所接觸到的基本都是有限的世界，所學的概念都有著較強的現實背景；而無理數涉及到了無限的現象，要讓學生更好地理解無理數的概念，教師需要在教學中培養學生無限的意識．從知識點的歷史發展看，學生有這種困境也是必然的．無理數從出現，到被廣泛接受，歷經了一千多年的時間，根據人類學習的歷史相似性，知識形成經歷如此漫長的發展過程，要讓學生在短短的一節課中接受和理解它是十分困難的．目前，已有很多學者對無理數的教學進行了研究，有教師介紹了自己的無理數教學經驗[10]，也有教師指出無理數教學所存在的幾種誤區[11]．有學者研究表明，學生雖然對無理數的形式定義掌握較好，但是存在概念表象比較單一、直覺與形式知識不一致、直覺與運算法則不一致等不足[12]．也有研究表明，職前教師對無理數和有理數的個數的理解比較弱[13]．在無理數的教學方面，有學者從定義、概念等7個方面對無理數的教學提出了建議[14]，也有研究表明可以用數學文化和數學史來幫助教師改進無理數教學[15]．

由此可見，雖然在無理數的教與學方面已有較多的研究，但是對于無理數教學中所需要的教師知識，以及影響因素有哪些還缺乏研究．這里就無理數的發展歷史對職前教師教學知識的影響情況進行分析．

3 研究過程與結果

3.1 研究方法與過程

不同的研究目的，需要不同的研究方法．一般來說，量化研究可以用來解決“是什么”的問題，而在研究“為什么”和“怎么樣”方面，質性研究更適合[16]．鑒于教學知識的內蘊性和復雜性，難以通過合適的量表來測量教師的教學知識，因此采用質性研究會更為清晰地了解教師內心的變化過程．在研究對象方面，從某高師院校的三年級數學師范生中隨機選取 10位進行研究，在研究中分別用 PT1-PT10表示．由于研究者即為數學史課程的授課教師，因此也屬于行動研究的范疇，研究者將通過數學史課堂內外的觀察，更好地了解職前教師教學知識的變化情況．

研究過程可分為5個步驟：

（1）要求職前教師在微格教室，對浙教版七年級上冊3.2實數的內容進行模擬教學（1課時），并提交教學視頻和教學設計．

（2）隨后，研究者向他們介紹了無理數的發展歷史，包括從公元前 Pythagoras學派發現無理數，到 Eudoxus和Archytas的新比例理論；從西方學者對無理數的排斥到東方學者對無理數的巧妙處理；從近代部分西方學者開始逐步接受無理數，到Weierstrass、Meray、Dedekind和Cantor等數學家所建立的無理數理論．以及無理數名詞的由來，無理數教與學的現狀，并向他們展示了若干數學史融入無理數教學的案例．

（3）在了解無理數的發展歷史后，職前教師對原先自己的模擬教學進行反思．

根據地質情況及結合以往施工經驗，采用CZ-8B型沖擊鉆機鉆劈成槽，采用先Ⅰ序槽段的施工方法。在同一槽段內，先施工單號主孔，后施工雙號副孔，主孔、副孔采用圓套方式劈打成槽。槽段造孔工作結束后，對造孔質量進行全面檢查驗收（包括孔位、孔深、孔徑、孔斜等），檢查合格后進行清槽換漿工序。

（4）反思過后，職前教師對原先的教學設計進行修改，并再次進行模擬上課，以及撰寫自己的心得體會．

（5）最后，研究者對職前教師逐一進行訪談，訪談的主要目的是為了解他們的無理數教學知識是否出現了變化？有什么變化？這些變化是否屬于數學史的影響？等等．訪談過程結合他們的模擬教學視頻和教學設計，以幫助訪談者進行刺激回憶．

3.2 研究結果

通過對職前教師的訪談，以及他們前后兩次教學視頻和教學設計的對比發現，職前教師在了解無理數發展歷史前后教學知識的變化情況存在較強的一致性，但是在變化強度方面存在較大的區別，具體變化情況如表1所示．

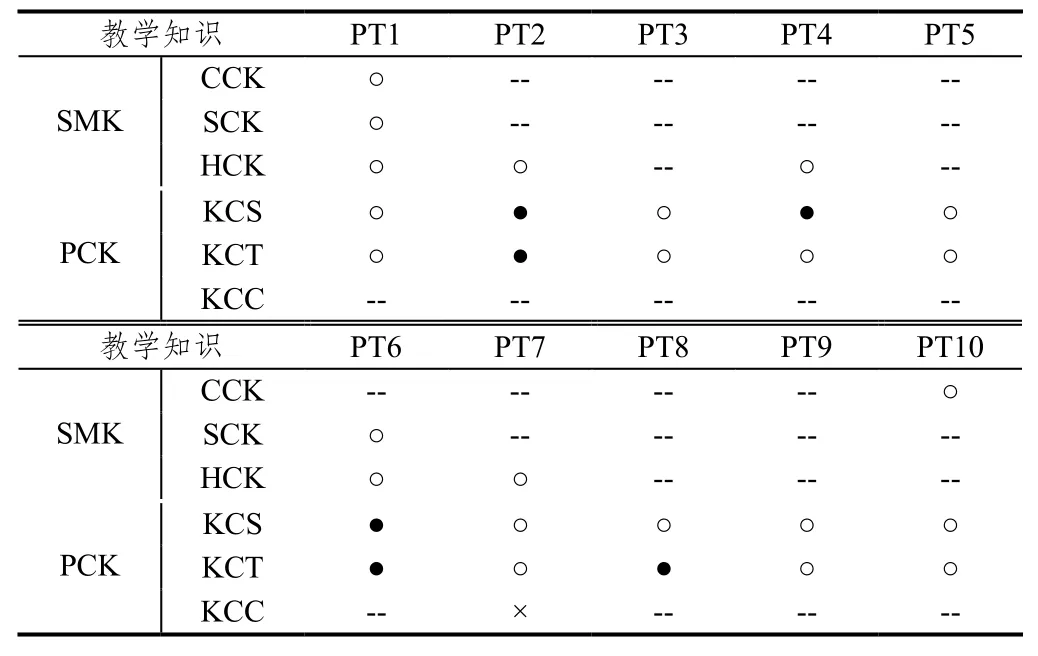
表1 職前教師學科內容知識變化情況

（1）數學史對教師學科內容知識的影響．

從表1可以看出，數學史對職前教師無理數教學的一般內容知識（CCK，主要指學科的本體性知識）和專門內容知識（SCK，指分析和解釋學科內容的知識，包括掌握多種解題方法、能解釋解題過程、分析錯誤原因等）有所影響，但變化不大．例如有部分職前教師是通過數學史的學習，才知道了可以用反證法來證明 2是無理數；也有部分教師通過數學史才了解無限不循環和兩數不可比之間的聯系．當然，也有部分教師是在這之前就知道了．相比較而言，在無理數教學的水平內容知識（HCK）方面，職前教師的變化更大一些．

教師的水平內容知識指教師能用聯系的視角看待數學，了解數學概念在不同階段的發展情況．在接觸實數數學史知識前，職前教師對實數的認識還是孤立的．例如在教學的開始階段，他們一般就會向學生介紹什么是無理數，進而用大量的時間來說明實數的分類，如何在數軸上表示實數等練習性內容．而在了解了無理數的發展過程以后，職前教師改變了這種認識，他們從歷史中知道了無理數概念的產生是社會發展的必要、無理數名稱的由來、歷史上無理數的各種定義、無理數和有理數個數的比較等，并都意識到只有從根本上理解了無限不循環，才能更好地理解無理數．從職前教師的訪談和教學反思中可證明他們的這種變化．

由此可看出，通過對無理數發展歷史的了解，職前教師知道了無理數存在的必要性，無限不循環的特點；了解了無理數的產生除了需要有理數的知識基礎以外，還需要分割理論，等等．這些都說明了，無理數的歷史幫助教師了解了無理數與其它知識點的聯系，屬于水平內容知識的范疇．

（2）數學史對教師教學內容知識的影響．

研究發現，與學科內容知識相比，數學史對職前教師無理數教學的教學內容知識有著更大的影響，尤其是在內容與教學知識（KCT）和內容與學生知識（KCS）這兩個方面．內容與教學知識是教師的數學知識與教學知識兩者的綜合體，具體體現在教師能根據不同的數學知識，設計合適的教學方式，選取合適的例子和練習題．從研究情況看，在數學史課程前，職前教師大多都是嚴格按照教材上的順序進行教學設計，對教學方式的優缺點也沒有深入的思考．但是在了解了相關的數學史內容后，他們都意識到無理數的發展不是一蹴而就的，是在長期的發展中逐步完善的．因此教學的設計不能過于簡單，而應該由易到難逐步遞進，需要對教學的重點和難點做更多的設計．因此，都在新的教學設計中增加了例子，或者具有數學文化背景的教學內容．教學中不僅更加重視了對學習無理數必要性的強調，還針對學生可能存在的疑慮進行了強化．例如，在研究中職前教師發現，無理數是無限不循環小數這一論述的理解是教學的難點，學生對“無限”過程中是否一直都會“不循環”會存有疑慮．因此在后期的教學中，多數職前教師融入了阿基米德的反證法，用較為通俗的語言向學生介紹了是無理數的證明過程．這不僅可以很好地消除學生的疑慮，突破教學難點，也在一定程度上體現了數學的嚴謹性．

內容與學生知識是教師關于學生學習特點和知識基礎，以及所教學的知識點的類型、難度等方面的綜合體，包括教師能估計學生可能的想法，可能遇到的困難等方面的知識．在了解無理數的歷史以前，職前教師的教學設計較為單一，教學內容和教學過程大多以教科書為參照。在簡單演示的無限循環性后，提出了無理數的概念，然后做練習．訪談表明，職前教師之所以這么設計，是因為他們覺得無理數概念比較簡單，學生應該能會比較容易理解．但是，在了解了無理數的相關歷史以后，職前教師意識到無理數是經歷了一千多年才被大家所接受，要學生很快理解無限不循環的含義是比較困難的，有必要減緩教學的坡度，增加理解性的內容或題目，此舉讓他們的教學設計更加合理．職前教師的訪談和教學反思都證明了他們的這一變化過程．

例如 PT4認為，原來對教學想的太簡單了，以為用課本那個表格，可以讓學生理解就是無限不循環的，從而接受無理數的概念，現在看來這種方式可能不太行，即使學生不反對無限不循環這種說法，他們的認知里并沒有真正理解這一過程；PT2認為，原來把學生想的太理想化了，認為他們應該很快就能接受無理數的概念，現在看看無理數被人接受經歷了如此長期曲折的過程，要讓學生很快理解無限不循環就太不現實了，應該設置一些情境，用例子來輔助說明，最重要的是要把無限不循環的這個特點講得清楚；PT6認為，原來的教學設計即使學生課堂上知道了什么是無理數，也屬于死記硬背，缺乏理解很快就會忘記的，從歷史中可得知要學生理解無理數的概念，應該讓學生充分地理解無理數的無限不循環，而不能簡單地拋出概念，然后要求他們不停地計算、解題．

由此可看出，職前教師從無理數的發展歷史中得到了借鑒，對無理數的教學有了更深刻的認識，認為對于無理數的概念不能簡單地一筆帶過，應該創設情境，讓學生充分地理解無限不循環的過程．可以說，數學史對職前教師無理數的教學內容知識產生了較大的影響．

但是，研究中也發現，數學史對個別職前教師（PT7）的內容與課程知識（KCC）產生了負面的影響．內容與課程知識指教師要了解數學內容在不同年級的課程中的出現順序以及難度等信息的知識．無理數的發展史上，畢達哥拉斯學派發現了畢達哥拉斯定理后，發現了直角邊為1的等腰直角三角形的斜邊長度無法表示成兩個數之比，導致了無理數的產生．受到這段歷史的影響，研究者發現有職前教師利用勾股定理引出無理數，這與教材中內容出現的次序是相悖的．因為在教材中，學生是先接觸無理數，此后才學習勾股定理的知識．由于歷史和課程教學內容的安排并不是完全不一致的，導致了數學史對個別職前教師無理數的內容與課程知識有了負面的影響．由此可看出，數學史對教師教學知識的影響也可能是負面的，尤其是在知識點的歷史發展順序和知識點在教科書中出現的次序不一致的時候．

4 研究結論

通過研究，發現數學史對職前教師無理數教學的學科內容知識有影響，但是幅度不大．對一般內容知識沒什么影響，在專門內容知識方面雖然有所促進，例如能正確的解釋并證明是無理數，但是還不能認為其有本質上的提升．只在水平內容知識方面有了一些提升，主要表現為了解了無理數和有理數的名詞來源，能用聯系的觀點看待無理數知識，也了解了無理數和高等數學之間的聯系，但是幅度還不大．

而數學史對職前教師無理數教學的教學內容知識有了較大提升，尤其是在內容與教學知識和內容與學生知識這兩個方面．這主要體現在，職前教師從無理數的發展歷史中意識到知識點是經歷了漫長的發展才逐步完善，才逐步被人所接受，學生要理解無理數不會那么容易，應該在概念的呈現中優化教學設計，通過創設情境、展示不同例子，或者增加具有數學文化背景的內容，讓學生更好地理解無理數，而不是簡單地引出概念后重復各種課堂練習．研究還發現，數學史對個別教師無理數的內容與課程知識產生了一些負面影響，這主要是由于教材中知識點出現的次序和歷史發展不完全一致引起的，后續研究需要引起重視．但是這點并不能掩蓋無理數的發展歷史有助于提升職前教師的無理數教學知識這一研究結論．

從研究中可看出，了解知識點的歷史，教師不僅可以擴大知識面，加深學科知識的理解，還可以從知識點的歷史發展中，更好地判斷學生接受知識點的難易度，從而讓教學設計更加合理．一些歷史素材可以直接或者間接作為教學素材呈現給學生，提升課堂的文化品味．數學史是一座大寶藏，如果認為數學史僅僅是可以讓教師在課堂教學中講一些數學故事，激發學生的學習興趣，這種認識是十分片面和狹隘的．研究表明，數學史可以提升教師的教學知識，促進教師的專業發展．讓教師的教學更有自信，也能更好地實現“立德樹人”的教育目的．研究也說明了，在教師教育中開設數學史課程，從教學的視角向職前教師闡述數學的發展歷史是十分有必要的．

[1]Cannon T. Student Teacher Knowledge and Its Impact on Task Design [D]. Brigham Young University, Provo, Utah, 2008.

[2]Begle E G.Teacher Knowledge and Student Achievement in Algebra[M]. SMSG Reports, No.9 Stanford: School Mathematics Study Group, 1972.

[3]Kahan J A, Cooper D A, Bethea K A. The Role of Mathematics Teachers’ Content Knowledge in Their Teaching: A Framework for Research Applied to a Study of Student Teachers [J].Journal of Mathematics Teacher Education, 2003, (6): 223-252.

[4]Cochran K F, DeRuiter J A, King R A. Pedagogical Content Knowing: An Integrative Model for Teacher Preparation [J].Journal of Teacher Education, 1993, 44(4): 263-272.

[5]An S, Kulm G, Wu Z. The Pedagogical Content Knowledge of Middle School Mathematics Teachers in China and the US [J].Journal of Mathematics Teacher Education, 2004, (7): 145–172.

[6]Ball D L, Thames M H, Phelps G. Content Knowledge for Teaching: What Makes It Special [J].Journal of Teacher Education, 2008, 59(5): 389-407.

[7]Tzanakis C, Arcavi A. Integrating History of Mathematics in the Classroom: An Analytic Survey [A]. In: Fauvel J, van Maanen J.History in Mathematics Education[C]. Dordrecht: Kluwer Academic Publishers, 2003.

[8]McBride C C, Rollins J H. The Effects of History of Mathematics on Attitudes toward Mathematics of College Algebra Students [J].Journal for Research in Mathematics Education, 1977, 8(1): 57-61.

[9]張俊忠．數學教育中數學史融入策略研究[J]．中國教育學刊，2014，（9）：79-82．

[10] 林曉明．初中數學“有理數與無理數”教學案例[J]．數理化學習，2013，（2）：91．

[11] 何本南．無理數在教與學中的誤區及其對策[J]．中小學數學（初中版），2009,（6）：11-12．

[12] 馮璟，陳月蘭．無理數的認識——對64名職前數學教師的調查研究[J]．中學數學月刊，2010，（2）：6-8．

[13] Sirotic N, Zazkis R. Irrational Numbers: The Gap Between Formal and Intuitive Knowledge [J].Educational Studies inMathematics, 2007, (65): 49–76.

[14] 楊秀娟．初中生對無理數概念的理解[D]．華東師范大學，2007．

[15] 龐雅麗，徐章韜．基于數學史的無理數概念的教學設計[J]．湖南教育（下），2010，（2）：40-43．

[16] 李士锜．數學教育研究方法論[M]．北京：科學出版社，2015．

Qualitative Study on the Influence of the History of Mathematics on Pre-Service Teachers’ Teaching Knowledge——A Case of the Irrational Number’s Teaching

HUANG You-chu
(Institute of Curriculum and Instruction, Nanjing Normal University, Jiangsu Nanjing 210097, China)

Teaching knowledge is teachers’ professional knowledge, has big implications for teachers’ teaching. In this study, research the influence of the history of mathematics on teachers’ teaching knowledge as the case of the irrational number. The study found that the history can improve pre-service teachers’ teaching knowledge. In subject matter knowledge, the history of mathematics can help pre-service teacher know more knowledge about the irrational number. The history of mathematics has more influence on the pre-service teachers’ pedagogical content knowledge, let them know student’s thinking more accurately, better judge the focus and difficulty of teaching, and make the teaching design more reasonable.

the history of mathematics; teaching knowledge; irrational number

G650

A

1004–9894（2017）01–0094–04

[責任編校：周學智]

2016–10–10

江蘇高校優勢學科建設工程資助項目（PAPD）；教育部人文社科項目——數學師范生教學知識發展研究（14YJC880022）

黃友初（1978—），男，浙江溫州人，副教授，南京師范大學教育學博士后流動站博士后，主要從事數學課程與教學論研究．