基于學業水平質量監測的初中生數學核心素養發展狀況調查

董林偉，喻 平

（1．江蘇省中小學教學研究室，江蘇 南京 210013；2．南京師范大學 課程與教學研究所，江蘇 南京 210097）

基于學業水平質量監測的初中生數學核心素養發展狀況調查

董林偉1，喻 平2

（1．江蘇省中小學教學研究室，江蘇 南京 210013；2．南京師范大學 課程與教學研究所，江蘇 南京 210097）

依據高中課程標準修訂組專家提出的6個數學核心素養，建立三級指標體系對其劃分水平，以江蘇省2016年中小學生學業質量監測的測試題目為工具，對全省 82 319名初中二年級學生作了測試，將其中涉及數學核心素養的分數作統計．大數據分析表明：（1）江蘇省初中二年級學生的6個數學核心素養在總體上達到較高水平；（2）初中學生數學核心素養的發展水平不平衡，在一些核心素養方面兩極分化現象比較突出；（3）城鄉、不同區域、不同類型學校學生的核心素養水平發展不平衡；（4）數學核心素養水平不存在性別差異．

學業水平監測；數學核心素養；初中學生

1 問題提出

研究基于兩個背景．

第一個背景：中小學生學業質量監測．隨著2001年課程改革的實施，為了對基礎教育質量進行監測，教育部借鑒國際經驗于2003年設立了“建立中小學生學業質量測試分析和反饋指導”項目．這個項目從2004年開始，每兩年組織一次，在小學三年級和初中二年級進行．江蘇省義務教育階段學生學業質量監測從2006年開始，在教育部項目組的框架中進行．自2014年起，江蘇省獨立實施義務教育階段學生學業質量監測，但整體框架和技術標準仍延續原有項目．質量監測與分析在省教育廳的部署下進行，嚴格依據課程標準，遵循國際上有關教育質量科學測試的要求，并采用9項指數全面體現“質量”內涵．測試范圍覆蓋全省所有市、縣（市、區）．測試后，分別在省、市、縣、校四級形成質量分析報告，全面呈現地方和學校課程教學質量情況，對教育教學的過程進行深入細致的診斷，為教育教學和管理改革提供依據．

第二個背景：核心素養的提出．在《教育部關于全面深化課程改革落實立德樹人根本任務的意見》中，明確界定了核心素養，即學生應具備的適應終身發展和社會發展需要的必備品格和關鍵能力．基于這種背景，教育部于2015年開始組織專家對高中課程標準進行修訂，要求把學科核心素養作為修訂課程標準的主線，圍繞學科核心素養制訂教學內容、評價標準和教材編制．目前，高中數學課程標準修訂組的專家提出了數學核心素養的基本成分：數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析，對6種核心素養作了三級水平劃分，新的高中數學課程標準即將出臺．同時，許多學者對數學核心素養也開展了相關的研究[1～3]．

顯然，第一個背景是一種現狀，第二背景是一種導向．盡管當下核心素養的提出源于高中課程改革，但是關注發展學生的核心素養是國內外教育改革的必然走向和趨勢．面對這種情況，江蘇省中小學教研室組織專家對高中數學核心素養的研究作了認真分析，率先把數學核心素養概念引申到初中和小學，參照高中數學課程標準修訂組專家對數學核心素養的研究成果并結合《義務教育數學課程標準（2011年版）》（以下簡稱《標準》），對義務教育階段數學核心素養作了內涵界定和水平劃分．在2016年的全省質量監測的初中數學學科，除了按照原有測試的框架和任務外，把數學核心素養的考察滲透到測試題目中，這是一種從單純考察知識學習結果到考察知識學習與數學核心素養發展雙重功能測試的嘗試，同時，通過這次測試希望從中了解當下初中學生數學核心素養發展的基本狀況．

2 初中學生數學核心素養解析

2.1 概念界定

《標準》指出；“在數學課程中，應當注重發展學生的數感、符號意識、空間觀念、幾何直觀、數據分析觀念、運算能力、推理能力和模型思想．為了適應時代發展對人才培養的需在，數學課程還要特別注重發展學生的應用意識和創新意識．”[4]這個描述指出了初中數學的所謂10個核心概念．將這10個核心概念與高中6個核心素養作對比，數據分析觀念與數據分析對應，運算能力與數學運算對應，推理能力與邏輯推理對應，模型思想與數學建模對應．這4個對應前后概念的描述，《標準》與高中課程標準修訂組專家的說法內涵基本一致，只是要求和程度上有所差異．

《標準》對于空間觀念的界定是：“空間觀念主要是指根據物體特征抽象出幾何圖形，根據幾何圖形想象出所描述的實際物體；想象出物體的方位和相互之間的位置關系；描述圖形的運動和變化；依據語言的描述畫出圖形等．”幾何直觀“主要指利用圖形描述和分析問題．借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果．幾何直觀可以幫助學生直觀地理解數學，在整個數學學習過程中都發揮著重要作用”[4]．上面的描述中，空間觀念有數學抽象成分，思維對象是幾何問題，而對幾何直觀的描述主要說的是它的功能．高中數學核心素養“直觀想象”的界定是：“直觀想象是指借助空間想象感知事物的形態與變化，利用幾何圖形理解和解決數學問題．主要包括：利用圖形描述數學問題，建立形與數的聯系，構建數學問題的直觀模型，探索解決問題的思路．”顯然，將初中空間觀念和幾何直觀兩個概念合并，其內涵與高中的直觀想象是基本一致的．

符號意識的涵義是指能夠理解并運用符號表示數、數量關系和變化規律，并用符號進行推理，本質上就是一個數學抽象的過程．數感包括對數字關系和數字模式的意識，以及運用這種對數字關系和數字模式的意識靈活地解決數字問題的能力[5]．意識的過程本身有抽象的元素蘊含其中，反映的是人對現實問題中數學要素的抽象．因此，把數感和符號意識合并與高中核心素養中的數學抽象對應．

至于應用意識和創新意識，它們分布于上述各個核心素養要素中．基于上述分析，初中數學核心素養與高中數學核心素養形成一一對應關系，換言之，初中數學核心素養也分為6個要素，簡單地描述為：數學抽象是指舍去事物的一切物理屬性，得到數學研究對象的思維過程；邏輯推理是指從一些事實和命題出發，依據邏輯規則推出一個命題的思維過程；數學建模是對現實問題進行數學抽象，用數學語言表達問題、用數學知識與方法構建模型解決問題的過程；直觀想象是指借助幾何直觀和空間想象感知事物的形態與變化，利用圖形理解和解決數學問題的過程；數學運算是指在明晰運算對象的基礎上，依據運算法則解決數學問題的過程；數據分析是指針對研究對象獲得相關數據，運用統計方法對數據中的有用信息進行分析和推斷，形成知識的過程．

2.2 核心素養的具體表現及水平劃分

高中課程標準修訂組的專家對 6個數學核心素養作了三級水平劃分，這種劃分有兩個問題，其一，是針對高中數學學習的特征劃分的，如果完全搬遷到初中數學學習中來，會有一定的不適應性；其二，3個水平對應的是高中結業、高考、高校自主招生的數學核心素養要求，對于非終結性考試的指導作用不大．有學者以學科核心素養生成的本源是知識為邏輯起點，提出了學科核心素養水平劃分為知識理解、知識遷移、知識創新三級水平[6]．因為命題的依據主要來自“學業質量監測”的要求，不完全是依據考察核心素養開展的，因此上面的兩種水平劃分不適用該研究．

針對初中數學核心素養的特殊性，在作水平劃分時要考慮；（1）初中數學核心素養的具體表現及水平應體現初中學生的年齡特點與認知水平．（2）初中數學核心素養不是獨立于知識、技能、思想、經驗之外的“神秘”概念，它綜合體現出對數學知識的理解、對數學技能方法的掌握、對數學思想的感悟及對數學活動經驗的積累．（3）數學核心素養的具體表現及水平劃分既要參考高中數學核心素養水平劃分框架，更要與《標準》所規定的相應的課程內容、目標及要求相適應．

基于這種思考，與高中數學核心素養水平劃分的二級指標體系不同，把初中數學核心素養的水平劃分為三級指標，一級指標是數學核心素養要素，二級指標是數學核心素養的具體表現，三級指標是每一種表現的水平．具體表現的涵義是把每個核心素養應當達到的目標作出一種分類，這個目標的確定依據《標準》對每一個內容的要求，同時參照高中數學核心素養水平劃分的二級指標體系，即將這個二級指標作分類處理．三級指標是對每一種數學核心素養的具體表現作出水平劃分，分為A、B、C、D四個水平，A水平最高，D水平最低，一般來說在某一維度處于高水平的學生也能完成較低水平的任務．附錄中表1～表6給出了每種核心素養的具體劃分描述．

3 試卷設計與被試情況

3.1 試卷設計

由于考試的時間為90分鐘，因此測試設計了A、B兩套試卷以確保測試內容具有一定的覆蓋面．但由于A、B卷的客觀難度不可能完全相同，又分別是不同學生群體作答，為保證兩卷的等值性，專門設計了S卷，S卷是由從兩份試卷中各抽取部分試題組成的，并由第三批學生作答．試卷的題型包括選擇題、填空題和解答題，其中A套試卷18題共26小題，B套試卷19題共27小題．測試內容僅限于初一、初二的課程內容．

需要說明的是，由于每一個數學核心素養在發現與提出、分析與解決數學問題和實際問題中，各自在不同的環節發揮不同的作用，而且相互“交著”相互“滲透”，同一個試題可能會涉及多個核心素養的體現．為此，選取該試題重點體現的一個核心素養進行分析統計．具體情況如表1．表1中題目的編號M指數學，8指年級，A代表A卷，B代表B卷，O代表客觀題，S代表主觀題；后面3個數字前面兩個指題號，后面一個指小題號．例如M8AS172指數學8年級A卷的主觀題，第17題第2小題．

3.2 數據處理

對于4個水平的分數處理采用Angoff方法．該方法按3個步驟進行[7]：

按照一定的要求選取一組領域評判者，對他們進行培訓，使其對于最低能力應試者的概念有較為清楚而統一的看法，并將這組應試者稱為邊界組考生，他們是達到某一標準最低水平的考生．

要求每一個評判者對于每一個題目做出這樣的判斷：邊界組考生正確回答該題目的概率是多少．

將某個評判者對該測驗中所有題目的判斷值相加，就是評判者認為邊界組考生應當得到的分數．計算所有評判者評分的平均值，就得到合格分數線．

選擇一組初中數學特級教師，正高級教師和教研人員，依據這個方法，分別定出優秀水平A、良好水平B、合格水平C、不合格水平D的分數線．

由于采用大樣本收集數據，因此對差異性分析沒有作統計檢驗．

3.3 被試選擇

表1 涉及數學核心素養的題目分布

表2 被試選擇情況

4 測試結果的整體分析

4.1 總體表現

學生在6個核心素養上的各水平表現如圖1．

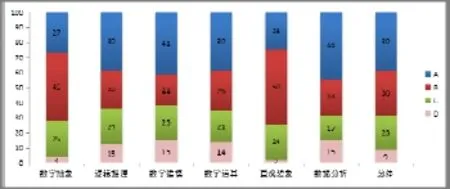
圖1 全體學生在數學6個核心素養上的各水平的人數比例

從圖1可以看出，初中二年級的學生中有超過90%的學生的核心素養綜合表現達到了合格及以上水平，其中有39%的學生達到了A水平．從數學核心素養的6個方面看，學生在邏輯推理、數學建模、數學運算和數據分析等4個方面達到A水平的人數分別達為39%、41%、39%和44%，但在這4個方面處于D水平的人數都超過了10%．學生在數學抽象、直觀想象等兩個方面達到 A水平的人數雖然只占到學生數的四分之一，但處于D水平的人數只有4%、2%，要明顯少于前4個方面．

4.2 不同群體學生的核心素養表現

學生群體按照區域劃分為蘇南、蘇中、蘇北，按照城鄉劃分為城區、鎮區、鄉村，按照學校性質分為公辦、民辦，按照性別分為男、女．

從圖2可以看出，不同地域的學生在數學核心素養總體表現存在差異，整體上蘇中略高于蘇南，都明顯高于蘇北，在邏輯推理、數學建模、數學運算、數據分析等方面優勢明顯．蘇南學生在邏輯推理、數學建模、數學運算、數據分析的A水平的人數比例分別達到42%、45%、43%、48%，但在邏輯推理、數學建模、數學運算和數據分析等4個方面仍處于D水平的人數比例都超過了10%；蘇中學生除了數學抽象、直觀想象外的 4個方面都有接近半數的學生達到 A水平，但在邏輯推理、數學建模、數學運算、和數據分析等4個方面都有10%左右的學生仍處于D水平；蘇北學生在邏輯推理、數學建模、數學運算、數據分析等4個方面也有三分之一的學生達到 A水平，但在邏輯推理、數學建模、直觀想象、數據分析等4方面有20%的學生仍處于D水平．

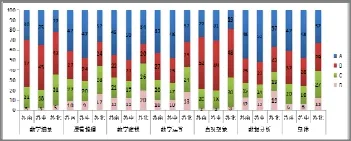
圖2 不同地域學生在數學6個核心素養上的各水平人數比例

從圖3可以看出，城區初中學生的數學核心素養總體表現都高于鎮區學生，且明顯高于鄉村學生，特別是在數學建模、數據分析等方面優勢更加明顯．城區學生在邏輯推理、數學運算、數據分析A的高水平的人數比例分別達到43%、 44%、49%，但在邏輯推理、數學建模、數學運算和數據分析等4個方面處于D水平的人數比例都超過了10%；鎮區學生除了數學抽象、直觀想象外的4個方面都有超過三分之一的學生達到A水平，但在邏輯推理、數學建模、數學運算和數據分析等4個方面都有15%左右的學生處于D水平；鄉村學生在邏輯推理、數學建模、數學運算、數據分析等4個方面也有超過四分之一的學生達到A水平，但在邏輯推理、數學建模、直觀想象等方面有超過四分之一的學生處于D水平．

評審工作流程更加嚴密。山東省各級財政評審機構以塑造工作流程為著力點，以防控評審風險為關鍵點，兼顧質量與效率，多措并舉，規范評審程序，提高管理水平，保證評審質量，確保評審工作公平、公正、高效開展。如，棗莊市采取完善評審資料流轉程序、制定項目評審預案、完善評審質量保障機制等6項措施，環環嚴謹相扣，層層壓實責任，將監督約束貫穿評審前中后全過程；泰安市按照工作項目化、項目目標化、目標責任化、責任績效化的“四化”要求，構建一體化評審體系、建立書面質疑清單制度、明確現場踏察規定3條措施，規范工作流程，細分評審步驟，明確職責到人，提高評審質量。

圖3 城鄉學生在數學6個核心素養上的各水平的人數比例

從圖4可以看出，民辦初中學校的學生的數學核心素養總體表現明顯高于公辦，在數學建模、數據分析方面優勢更加明顯．公辦學校學生在邏輯推理、數學運算、數學建模、數據分析等4個方面都有超過三分之一的學生達到A水平，但在邏輯推理、數學建模、數學運算、數據分析等4個方面都有15%左右的學生處于D水平；民辦學校學生在邏輯推理、數學建模、數學運算、數據分析等4個方面都有超過半數的學生達到 A水平，但在數學建模、數據分析和數學運算等3個方面有超過5%的學生處于D水平．

圖4 不同性質學校的學生在數學6個核心素養上的各水平人數比例

從圖5中可以看出，初中男女學生的數學核心素養總體表現上沒有差異，都有接近40%的學生達到A水平，處于D水平的人數都低于10%，但在數學建模、數據分析、邏輯推理、數學運算等4個方面都有15%左右的學生仍處于D水平．

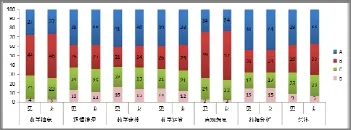
圖5 不同性別學生在數學6個核心素養上各水平人數比例

4 討 論

這次作的大數據測試，盡管測試標準是按照學業水平質量監測擬定的，不是嚴格意義上對學生核心素養發展的全面檢測，但嘗試在測試題目中加入了測量數學核心素養的要素，得到的數據在一定程度上反映了江蘇省初中二年級學生數學核心素養的基本狀況．

首先，從整體情況看，江蘇省初中二年級學生的6個核心素養達到了比較高的水平，在 A水平層面，邏輯推理、數學建模、數學運算、數據分析表現更好，但也正是這 4個方面，D水平的百分比較大，因而這4個因素的發展水平分化現象更加突出．數學抽象和直觀想象的B水平人數多，D水平的人數最少，反映了這兩個要素的集中趨勢．產生這種現象的原因可能是由于數學建模與數據分析對初二年級學生而言是一個比較新的內容，思維方式發生了變化，使許多其他素養不高的學生不能適應，而其他素養高的學生會很快適應，于是產生了分化現象．

其次，從不同群體的數據反映出在總體方面，蘇中地區學生的數學核心素養形成水平略高于蘇南地區，蘇中與蘇南都明顯高于蘇北，體現出一定的地區差異．3個地區在數學建模和數據分析方面處于 D水平的比率較大，兩極分化現象比較突出．從不同類型的學校看，城區初中學生的數學核心素養總體表現都高于鎮區學生，且明顯高于鄉村學生，特別是在數學建模、數據分析等方面優勢更加明顯．這個結果反映出城鄉之間存在差異，折射出教育發展的不均衡性．從性別差異看，男女生在6個核心素養方面不存在差異．

5 結 論

（1）江蘇省初中二年級學生的6個數學核心素養在總體上達到較高水平，其中在邏輯推理、數學建模、數學運算、數據分析等4個要素上達到A水平的比率更大．

（2）初中學生數學核心素養的發展水平不平衡，特別邏輯推理、數學建模、數學運算、數據分析等4個要素方面兩極分化現象比較突出．

（3）不同區域、不同類型學校學生的核心素養水平發展不平衡，蘇中地區略高于蘇南地區，蘇中與蘇南都明顯高于蘇北；城區總體表現都高于鎮區，且明顯高于鄉村；民辦學校總體表現明顯高于公辦學校．

（4）男生與女生的數學核心素養水平不存在顯著差異．

[1]鄭毓信．數學教育視角下的“核心素養”[J]．數學教育學報，2016，25（3）：1．

[2]喻平．數學學科核心素養要素析取的實證研究[J]．數學教育學報，2016，25（6）：1．

[3]王光明，張楠，周九詩．高中生數學素養的操作定義[J]．課程·教材·教法，2016，（7）：50．

[4]中華人民共和國教育部．義務階段數學課程標準[M]．北京：北京師范大學出版社，2011．

[5]徐文彬，喻平．“數感”及其形成與發展[J]．數學教育學報，2007，16（2）：8．

[6]喻平．發展學生學科核心素養的教學目標與策略[J]．課程·教材·教法，2017，（1）：48．

[7]余嘉元．Angoff方法有效性的檢驗研究[J]．教育研究與實驗，2008，（1）：54．

附錄：核心素養的具體劃分描述

表1 數學抽象的具體表現與表現水平

表1 （續） 數學抽象的具體表現與表現水平

表2 邏輯推理的具體表現與表現水平

表3 數學建模的具體表現與表現水平

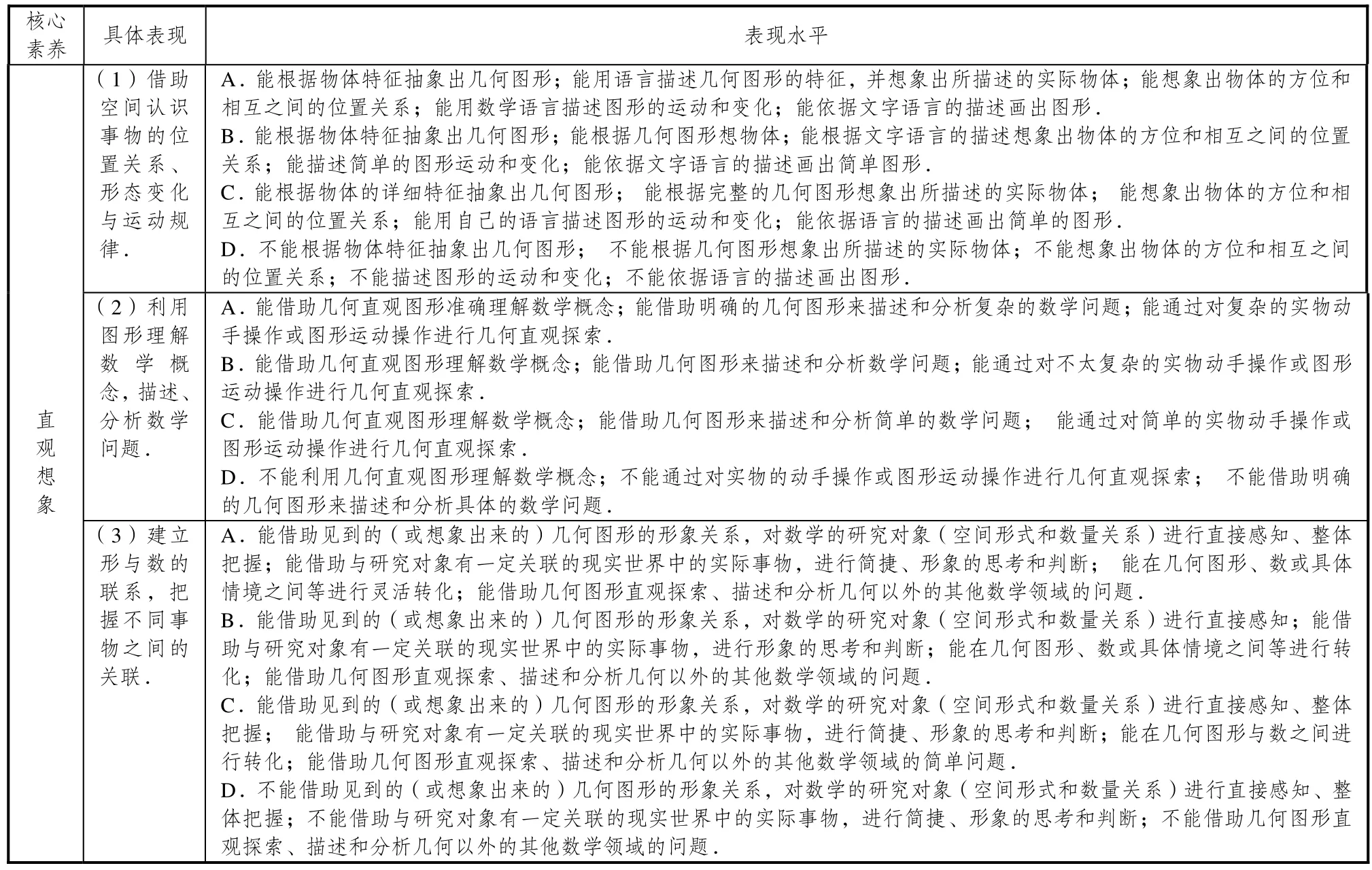
表4 直觀想象的具體表現與表現水平

表5 數學運算的具體表現與表現水平

表6 數據分析的具體表現與表現水平

[責任編校：周學智]

Investigation on the Development of Mathematical Key Competencies of Junior High School Students Based on the Academic Level Monitoring

DONG Lin-wei1, YU Ping2
(1. Teaching Research Office Jiangsu Provincial Department of Education, Jiangsu Nanjing 210013, China; 2. Research Institute of Curriculum and Teaching, Nanjing Normal University, Jiangsu Nanjing 210097, China)

Three-level index system is established based on the six math key competencies which revised by senior high school curriculum standard revisionists. 82 319 Grade 8th students in Jiangsu Province are tested by using items from the 2016 Jiangsu Primary and Middle School Students Academic Level Monitoring Test, and their math key competencies scores are analyzed in detail. The big data analysis shows that: (1) The six math key competencies of 8th grade students in Jiangsu province have achieved overall higher levels; (2) Their math key competencies level is unbalanced and polarized in some aspects. (3) The math key competencies of high school students is uneven developed and there is polarization exists among different schools and regions. (4) No gender difference was found in the level of math key competencies.

academic level monitoring; mathematics key competencies; junior high school students

G632

A

1004–9894（2017）01–0007–07

2017–01–20

江蘇省教育廳基于測試分析的跟進式改革重大研究項目——義務教育學科核心素養和關鍵能力研究（2015JYKTZD-02）；江蘇省中小學教學研究第十一期重點課題——初中數學學業水平評價研究（2015JK11-Z085）；江蘇省社科基金——中小學生數學核心素養體系建構與教學實踐研究（15JYD001）

董林偉（1965—），男，江蘇宜興人，特級教師，教授級高級教師，主要從事數學教育研究．