裝甲裝備貴重、低消耗可修復備件兩級庫存配置建模與仿真

(1. 陸軍裝甲兵學院裝備保障與再制造系， 北京 100072； 2. 61377 部隊， 廣東 深圳 518017)

可修復備件是指通過采用經濟可行的技術手段可恢復原有功能的備件[1]。隨著裝備的升級換代和部隊換件修理的廣泛展開，在裝甲裝備保障費用中，價格昂貴而又不經常消耗的可修復備件所占比重越來越大[2]。該類備件通常在裝備戰斗力生成過程中發揮著關鍵作用，且一般生產周期較長，因而需預先儲備一定數量的庫存；但由于其價格昂貴且技術含量高，過量儲備既費財力又易因積壓而失效。通過完善貴重可修復備件保障機制，使故障件得以及時修復和有效再利用，對降低備件庫存數量、節約備件保障經費、提高備件保障效率和效益具有重要意義。

與不可修復備件相比，可修復備件涉及故障件的回收與修復等，因此，其庫存控制問題更為復雜。SHERBROOKE[3]最早提出的METRIC(Multi-Echelon Technique for Recoverable Item Control)模型是可修復備件庫存控制的理論基礎，應用十分廣泛。羅祎等[4]基于該模型建立了三級庫存體系的備件配置模型；阮旻智等[5]增加了備件體積和質量約束，建立了面向任務的艦船攜行備件配置模型；聶濤等[6]研究了該模型在K-N冗余雷達系統備件供應優化中的應用。然而，上述研究在建模時均基于“無限修復能力”這一假設，即故障件在修復時不存在排隊等待的情況，這會導致模型計算結果出現一定誤差。因此，文獻[7-9]作者放寬了無限修復能力假設，基于排隊論對METRIC模型進行了修正，但大都只考慮了有限修復能力對“在修復數量”這一隨機變量均值的影響，而未考慮對其方差的影響。另外，上述研究成果大都假設備件完全修復、不存在報廢，且多以裝備使用可用度作為保障效能評價指標，不符合裝甲裝備保障實際，也未通過有效的方法對模型的準確性進行驗證。

為了解決上述問題，筆者對裝甲裝備貴重、低消耗可修復備件的“基地-部隊”兩級供應保障機制進行描述；綜合考慮有限維修渠道、報廢率等因素，建立備件配置模型，并運用邊際分析法進行求解。最后，通過算例分析驗證模型的可信性和有效性。

1 備件保障機制描述

根據經濟訂貨批量模型(Economic Ordering Quantity，EOQ)，采取(s，S)庫存策略時年度費用CT(包括產品價格費用、訂貨費用和庫存持有費用)的計算公式為

(1)

式中：D為產品年需求量；CP為產品單價；Q為每次訂貨批量；CO為每次訂貨固定費用；H為單位產品年庫存持有費用(通常設定為產品單價CP與常數k的乘積)。對式(1)求Q的導數，并令其為0，得到年度費用最低時的最佳訂貨批量

(2)

圖1為EOQ模型中產品最佳訂貨批量，反映了CO=0.5，k=0.1時，Q*隨D和CP變化的趨勢。可以看出：當D< 2件且CP> 2萬元時，Q*值會接近于1。也就是說，當產品價格很高、消耗率很低時，每消耗1件備件就需要1次訂貨。結合可修復備件保障實際，每當換件修理消耗1件庫存，應立即向上級申請1件補給，同時，上交故障件進行修復。這種方式可最大限度地減少可修復備件庫存配置數量，降低保障費用，同時，縮短故障件的修復周期，提高可修復備件的利用率。

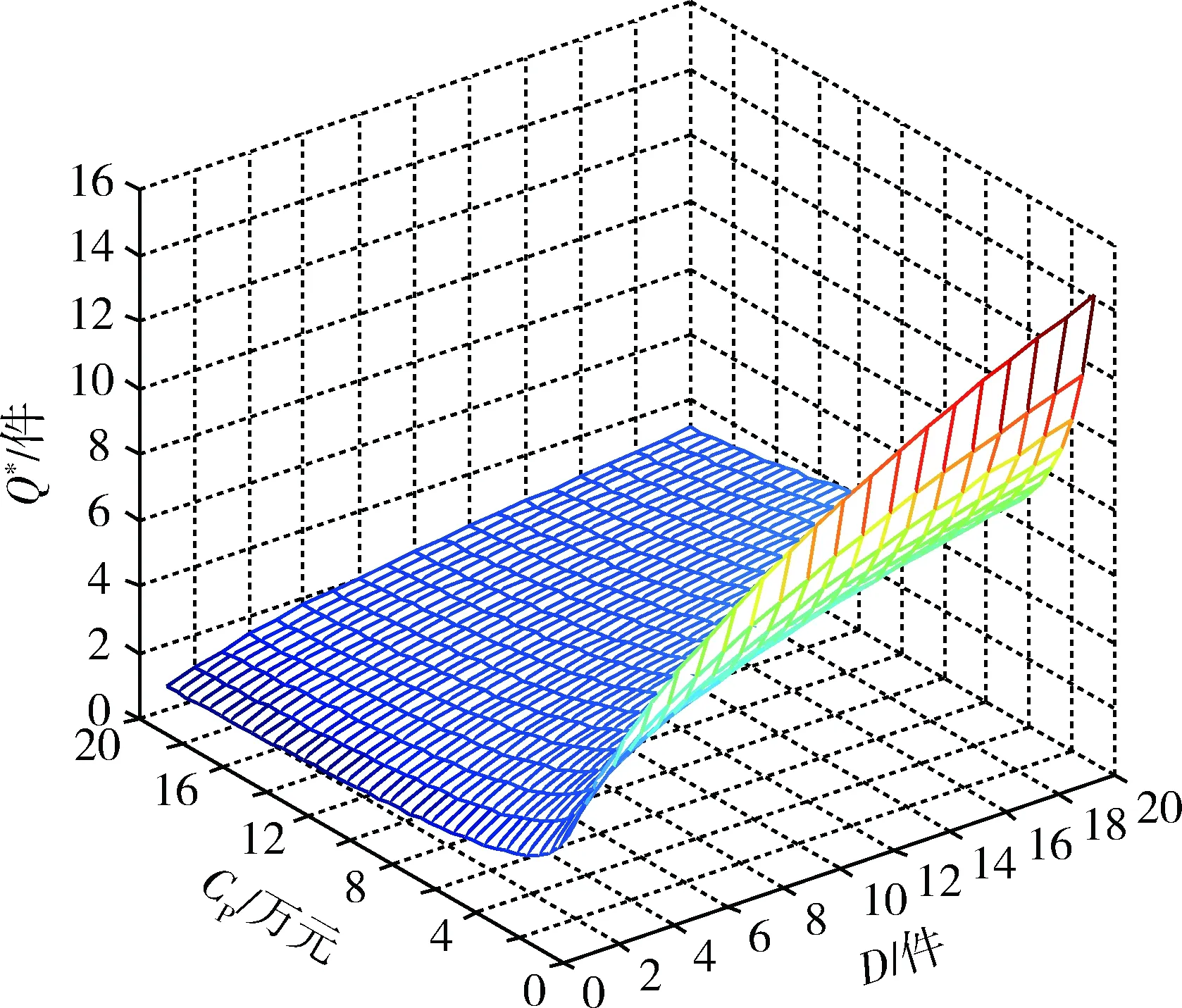
圖1 EOQ模型中產品最佳訂貨批量

根據上述分析，裝甲裝備貴重、低消耗可修復件的“基地-部隊”兩級保障運行機制如圖2所示。

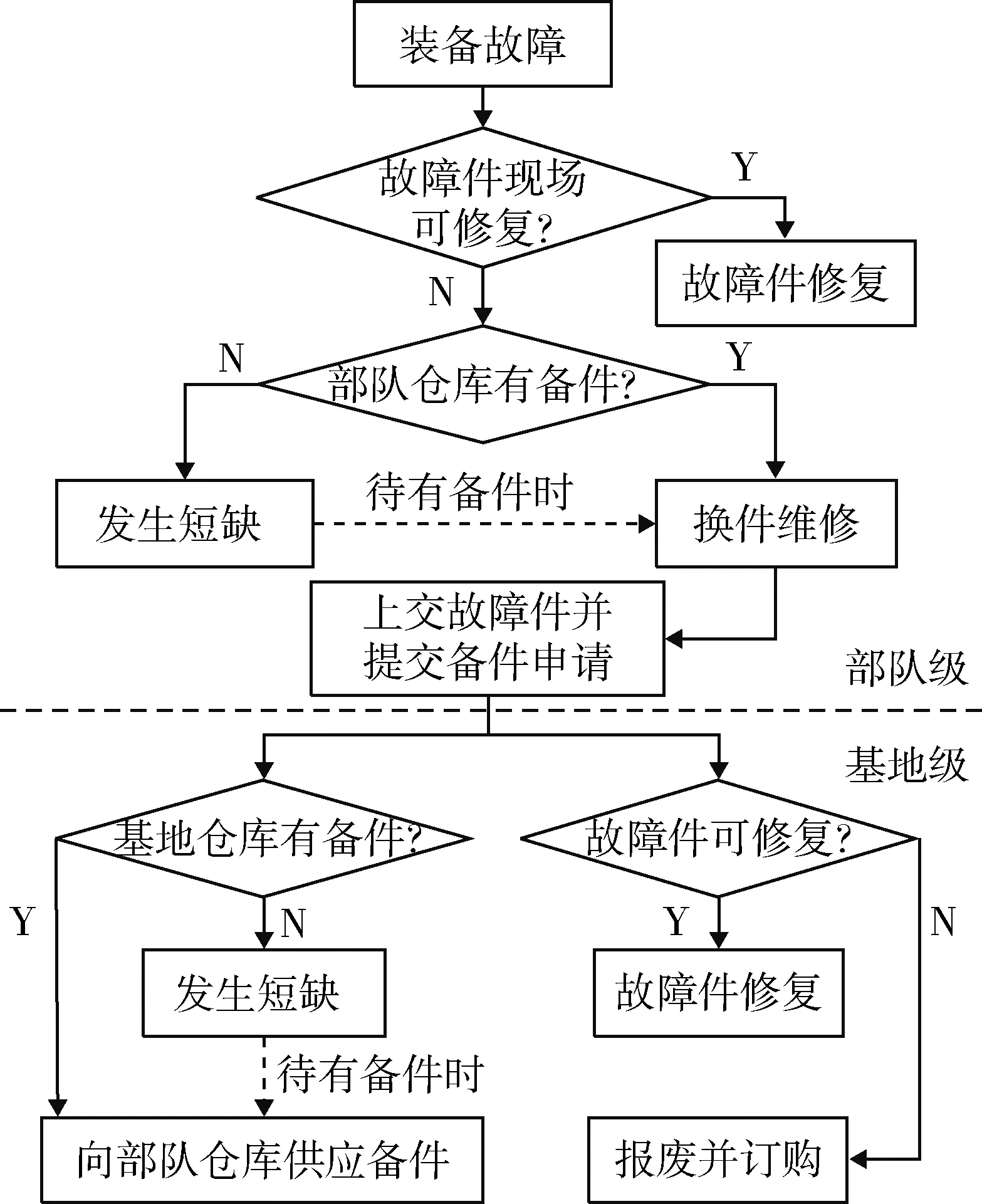
圖2 裝甲裝備貴重、低消耗可修復件兩級保障機制

基地級保障機構由基地倉庫和基地維修機構組成，部隊級保障機構由部隊倉庫和部隊維修機構組成。當部隊裝備發生故障，定位到故障部件后，若故障比較簡單，則可借助廠家直修、戰區巡修或部隊檢修等形式進行現場快速修復；否則，從部隊倉庫中調撥備件進行換件維修，若庫存量為0，則等待庫存補給到達后再進行換件維修。從裝備上拆下的故障件上交基地倉庫，同時向基地倉庫申請1件備件。基地倉庫接到申請后，從本級倉庫中調撥1件備件供應該部隊倉庫，若庫存數量為0，則等待庫存補給到達后再行供應。基地倉庫接到故障件后，根據修復能力和修復范圍，分為戰區修理大隊、大修工廠或生產廠家3種情況進行修復，修復后的備件存入基地倉庫；若不能修復，則該故障件報廢，由基地倉庫向廠家訂購1件新品以維持整體庫存水平。

2 備件庫存配置建模

Palm定理是METRIC模型的理論基礎，它假設故障件的修理時間相互獨立，即維修機構具有無限的修復能力，故障件修復時不需要排隊等待。然而，在實際工作中，當故障件修復時間較長時，忽略排隊等待時間，會明顯低估備件短缺量，從而影響模型的準確性。因此，筆者引入M/M/c排隊模型，在有限修復能力下，建立考慮報廢率的可修復件庫存配置模型。

2.1 模型假設

為便于分析和計算，首先對備件保障過程作如下假設：

1) 每次裝備功能失效都是由單一部件故障引起的；

2) 基層各項備件需求相互獨立，均服從穩態泊松分布；

3) 故障件立即送修，且修復如新；

4)修復故障件所需子級備件充足，無短缺；

5)不存在串件拼修和橫向調劑供應。

2.2 模型構建

在“基地-部隊”兩級保障機制下，部隊備件滿足率取決于備件庫存配置數量和待接收備件數量。設某基地下的部隊倉庫數為I，對某型裝甲裝備共J項可修復備件進行庫存配置，則在有限修復能力下，部隊倉庫i(i=1, 2,…,I)的第j(j=1, 2,…,J)項備件某一時刻的待接收數量Xij由以下2部分構成：

(3)

式中：λij和rij分別為部隊倉庫i的第j項備件的故障率和現場可修復概率；Oi為部隊倉庫i從發出備件申請到接收備件的時間。

基地倉庫第j項備件的需求率為

(4)

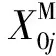
(5)

(6)

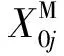
(7)

(8)

(9)

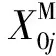
(10)

綜合式(7)、(8)、(10)可知：X0j的均值和方差分別為

(11)

(12)

記Pr(x0j)為X0j的概率分布，根據常見的離散分布統計特性，若D(X0j)/E(X0j)≈1，則Pr(x0j)選擇泊松分布；若D(X0j)/E(X0j)>1，則Pr(x0j)選擇負二項分布；若D(X0j)/E(X0j)<1，則Pr(x0j)選擇二項分布。若基地倉庫第j項備件庫存配置數量為S0j，則其短缺數B(S0j)的均值和方差分別為

(13)

D[B(S0j)]=E[B2(S0j)]-E2[B(S0j)]，

(14)

(15)

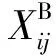
(16)

fij2D[B(S0j)]。

(17)

式中：fij=λij(1-rij)/λ0j，為基地倉庫第j項備件需求量中來自部隊倉庫i的備件所占比例。

綜合式(3)、(16)、(17)，Xij的均值和方差分別為

(18)

(19)

記Pr(xij)為Xij的概率分布，同樣可根據常見的離散分布統計特性確定其分布類型。

目前，常見的可修復備件庫存配置模型大都以裝備使用可用度作為備件保障效能評價指標。但我軍裝甲裝備在動用過程中遵循“滾動式循環動用”原則，并根據摩托小時儲備將裝備分為戰備車和教練車，其中教練車又分為控制用車、一般用車和重點用車。各類裝備實行區別動用和戰教輪換，重點用車動用頻繁，易發生故障；戰備車和控制用車基本不動用，裝備完好性較好。因此，利用裝備使用可用度來衡量所有裝備的可用性是不合理的。

針對這一情況，筆者選用備件滿足率作為備件保障效能評價指標。備件滿足率是指需要備件時不缺件的概率[10]，可根據備件庫存配置數量和供應渠道概率分布計算得出。若部隊倉庫i第j項備件庫存配置數量為Sij，則其備件滿足率為

(20)

進一步可得系統備件滿足率為

(21)

一般情況下，備件庫存配置建模的目標是在滿足規定的備件滿足率的前提下，使備件庫存配置費用最低。因此，備件配置模型可描述為

(22)

式中：C為備件配置費用;cj為第j項備件的單價;φ為設定的保障效能指標最低值。

3 模型求解

邊際分析法是求解METRIC模型最常用的方法。與遺傳算法等群智能優化算法相比，邊際分析法過程簡單、結果穩定，不會丟失最優解，在解空間規模不是特別大的情況下非常適用。因此，筆者選用該方法來求解模型。

式(22)中的決策變量為記錄基地和部隊倉庫各項備件庫存量的(I+1)×J維矩陣

(23)

該模型的邊際分析法求解過程如下：

1) 初始化決策變量S=0。

2) 通過不斷地迭代執行邊際分析(在每次迭代過程中，遍歷決策變量矩陣的每個位置)，依次計算其邊際效益值

(24)

式中：O為與S結構相同且第i行第j列值為1、其他位置為0的0-1矩陣。

3) 將最大的邊際效益值max(Δij)所對應的決策變量S中位置Sij的值加1，即Sij=Sij+ 1。

4) 根據式(21)計算系統備件滿足率F，若F≥φ，則停止迭代，決策變量S所表示的方案即為最優備件配置方案；否則，返回步驟2)，繼續迭代。

4 備件保障過程仿真

通過仿真對裝甲裝備貴重、低消耗可修復備件兩級供應保障過程進行動態模擬，統計相關保障效能指標，并與模型計算結果進行比較，驗證模型的準確性和可行性。基于Agent的建模與仿真(Agent-Based Modeling and Simulation，ABMS)方法是隨著分布式人工智能技術的發展而逐漸興起的一種建模技術。其中Agent是系統仿真模型的基本組成單元，可理解為具有自治性、社會性、主動性和反應性等智能特征的個體，能夠適應環境變化，并主動執行任務[11]。ABMS通過Agent之間、Agent與環境之間的交互和協作，可更加真實地還原系統的結構和運行情況，因而被廣泛地應用于復雜系統建模與仿真研究中。“基地-部隊”兩級保障機制下備件保障過程仿真Agent的層次結構如圖3所示。

ABMS是一種典型的面向對象的建模仿真方法，因而面向對象方法中的分析、設計與實現技術都可被借鑒到ABMS中，如統一建模語言(Unified Modeling Language，UML)等[12]。時序圖是UML動態模型圖之一，與Petri網等形式化語言相比，它可更加直觀地展示系統中Agent間交互行為發生的先后順序以及觸發交互行為的事件或消息。備件保障過程仿真Agent時序圖如圖4所示。

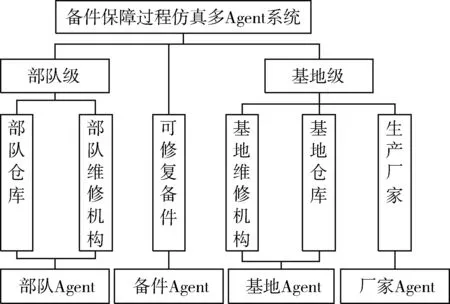
圖3 “基地-部隊”兩級保障機制下備件 保障過程仿真Agent的層次結構

圖4 備件保障過程仿真Agent時序圖

5 算例分析

5.1 算例求解

現對由Z戰區及其下屬2個旅(1旅和2旅)組成的兩級備件供應保障系統進行庫存配置。2個旅向Z戰區申請備件所需時間分別為O1=0.04 a，O2=0.08 a。某型裝備在2個旅的列裝數量均為50臺，該型裝備的中小修用備件約有1 000項，從中選取來自4個子系統的12項需求率低、價格高的可修復備件進行庫存配置，其參數設置如表1所示。

設定φ=0.90，運行邊際分析法求解模型，經過91次迭代后，得到備件最佳庫存配置優化結果及備件滿足率如表2所示，系統備件滿足率F=0.904，備件配置費用C=309.4萬元。由庫存配置結果可以看出：各項備件均以戰區集中儲存為主，旅基本不儲或少量儲存。與各旅分散儲存相比，戰區集中儲存的備件可供各旅共同使用，因而以更少的備件實現相同的保障效果。

為了分析有限修復能力對庫存配置模型準確性的影響，利用標準VARI-METRIC模型[3]和文獻[1]的修正模型，分別計算1旅(i=1)的備件庫存配置方案對應的備件滿足率，結果如表3所示。可以看出：不考慮修復能力的影響會高估備件滿足率；且與文獻[1]模型相比，本文的庫存配置模型對有限修復能力影響的修正效果更加明顯。

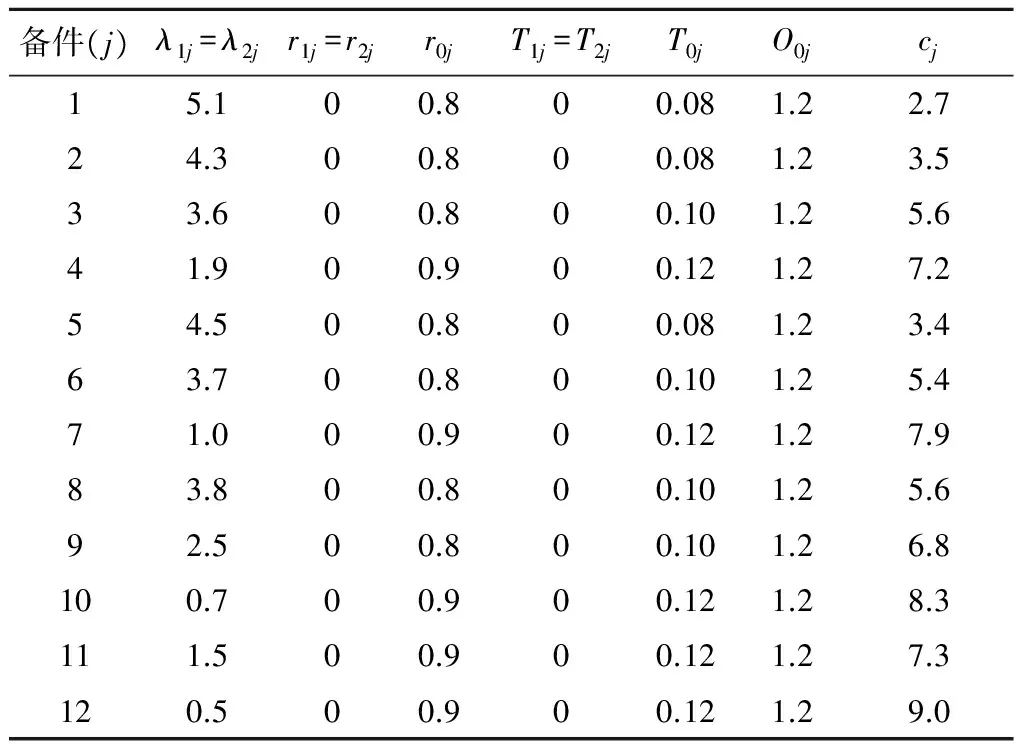
表1 備件參數設置

注：時間單位為年(a)；價格單位為萬元。

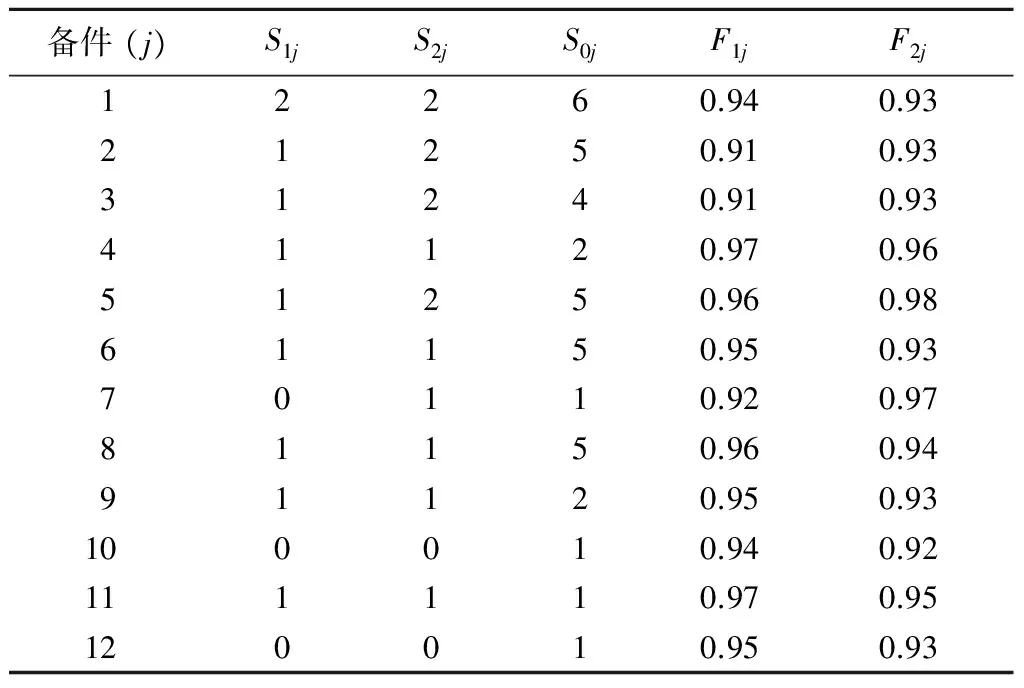
表2 備件庫存配置優化結果

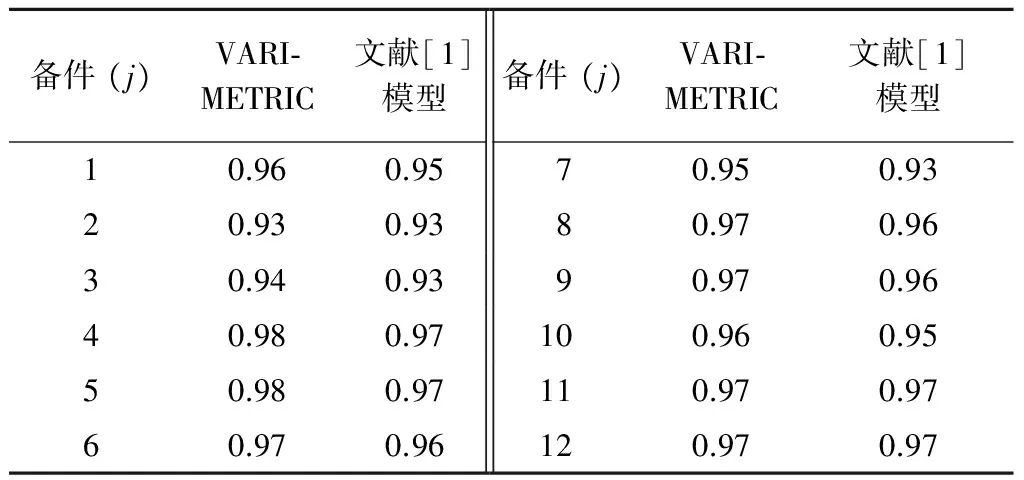
表3 1旅倉庫備件滿足率F1j對比

5.2 仿真驗證

Anylogic是一款新興的、基于JAVA語言的系統建模仿真平臺，同時支持離散事件系統建模、系統動力學建模、基于Agent的建模等多種建模方式；提供了友好的可視化界面，通過簡單的編程即可實現復雜的邏輯功能；支持普通仿真、蒙特卡羅仿真、優化仿真、比較運行、敏感性分析等多種仿真實驗。因此，筆者選擇Anylogic平臺對第5.1節算例進行仿真。仿真系統框架如圖5所示。

圖5 仿真系統框架

部隊備件滿足率是本文庫存配置模型的核心指標，故將其作為檢驗模型準確性的統計變量。根據定義，備件滿足率為備件庫存數量不小于0的時間與仿真運行時間之比。在Anylogic中設置2種實驗類型進行仿真：

1) 設置實驗類型為普通仿真，觀察備件保障過程中各項系統指標的實時變化情況。設仿真時間單位為月，即每秒推進1個月。在仿真過程中，1旅倉庫前3項備件(j=1,2,3)的庫存數量和備件滿足率的實時變化情況分別如圖6、7所示。可以看出：每當備件發生短缺時，其滿足率隨即變小。

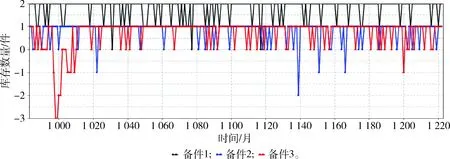
圖6 1旅倉庫備件庫存數量實時變化曲線

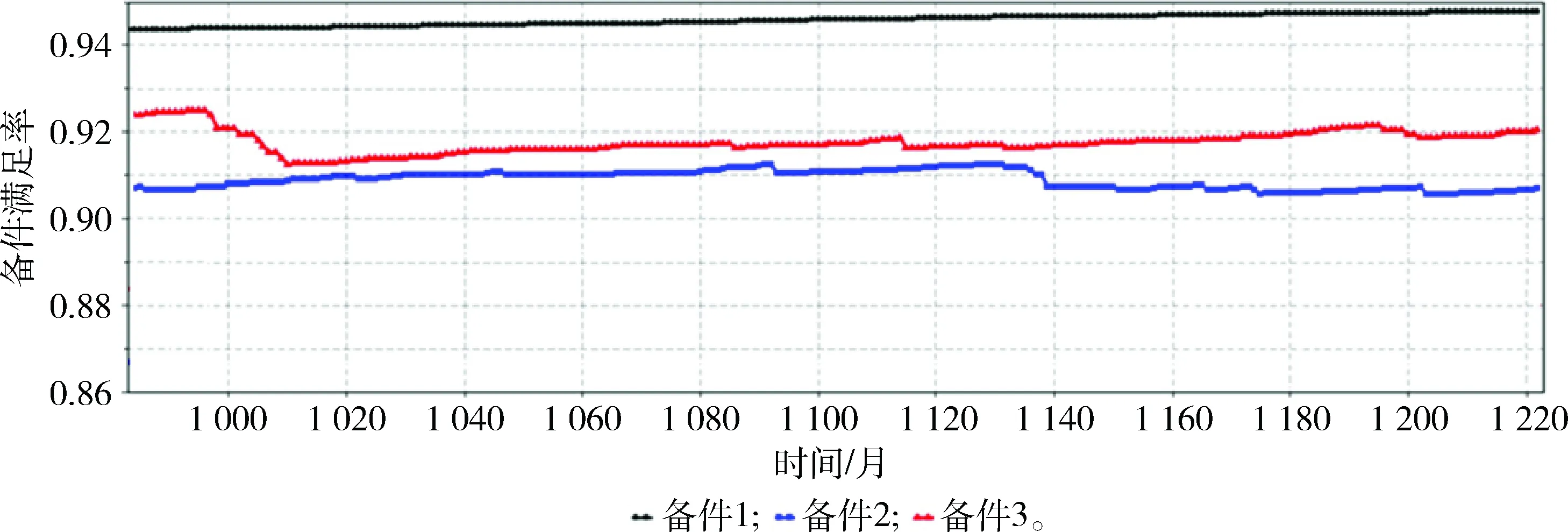
圖7 1旅倉庫備件滿足率實時變化曲線

2) 設置實驗類型為蒙特卡羅仿真，驗證模型準確性。設置仿真次數為100次，每次仿真運行周期P=1 200月；為了消除初始狀態對系統指標的影響，只對后1 000個月進行統計分析。分別統計2個指標的仿真樣本均值和標準差，利用終止型序貫程序法[13]得到置信度為90%的置信區間，如表4所示。

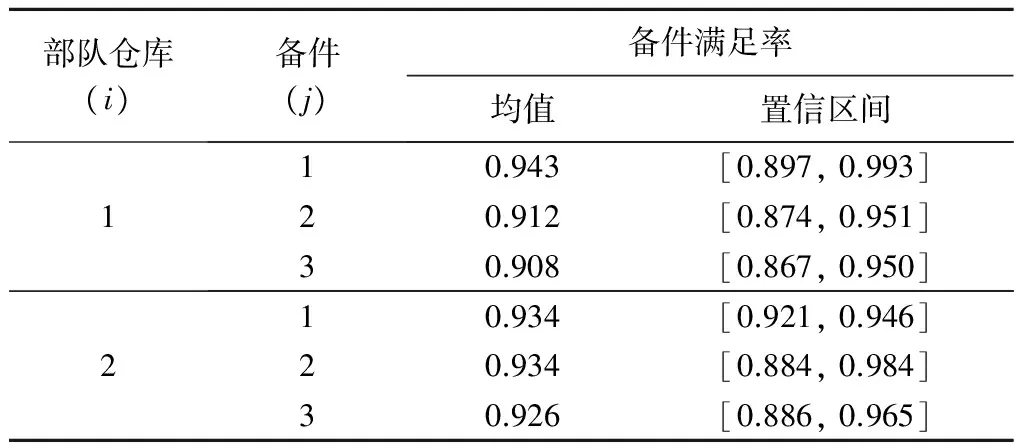
表4 仿真樣本統計分析結果

將仿真得到的置信區間與表2、3中模型計算的備件滿足率進行對比可知：模型計算結果都落在了置信區間內，且與標準VARI-METRIC模型和文獻[1]模型計算結果相比，本文提出的庫存配置模型的計算結果更接近仿真樣本均值。

6 結論

筆者以裝甲裝備貴重、低消耗可修復備件為研究對象，綜合考慮報廢率、有限修復能力等因素，建立了兩級庫存配置模型，設計了模型的求解算法，并通過仿真驗證了模型的可信性和有效性。通過研究發現：對于該類備件，應以基地倉庫集中儲存為主，部隊倉庫基本不儲或少量儲存；且修復能力的有限性對該類備件庫存配置模型的可信性和有效性有一定的影響，在建模時應予以考慮。本文的研究成果對提高裝甲裝備備件保障效益、完善備件保障機制具有一定的參考意義。

參考文獻：

[1] 張帥，李軍亮，呂衛民，等.有限維修能力下艦載機可修復件庫存優化模型[J].北京航空航天大學學報，2015，41(6)：1034-1041.

[2] 王慎，李慶民，王文斌，等.面向兩級可修復備件庫存系統的動態管理模型[J].計算機集成制造系統，2015，21(3)：788-799.

[3] SHERBROOKE C C.Optimal inventory modeling of system: multi-echelon techniques [M].2nd ed.Boston:Artch House，2004：35-42.

[4] 羅祎，阮旻智，袁志勇.多級維修供應下可修復備件庫存建模與優化[J].系統工程理論與實踐，2013，33(10)：2623-2630.

[5] 阮旻智，傅健，周亮，等.面向任務的作戰單元攜行備件配置優化方法研究[J].兵工學報，2017，38(6)：1178-1185.

[6] 聶濤，盛文.K:N系統可修復備件兩級供應保障優化研究[J].系統工程與電子技術，2010，32(7)：1452-1455.

[7] LAU H C，SONG H.Multi-echelon repairable item inventory system with limited repair capacity under non-stationary demands [J].International journal of inventory research，2008，1(1):67-92.

[8] 徐立，李慶民，胡毅鈞，等.有限維修能力下多級保障系統裝備時變可用度評估及保障方案優化[J].國防科技大學學報，2017，39(1)：128-136.

[9] YOON H, JUNG S, LEE S.The effect analysis of multi-echelon inventory models considering demand rate uncertainty and limited maintenance capacity [J].International journal of operational research, 2015, 24(1):38-58.

[10] 張志華，應新雅，費廣玉.串聯系統備件滿足率分配及配置優化[J].系統工程理論與實踐，2015,35(11)：2987-2992.

[11] 白金鵬，李天.面向指標論證的戰斗機突防效能評估[J].航空學報，2016，37(1)：122-132.

[12] 李雄，蒲瑋，唐亞林.基于UML的戰時裝備維修保障行動建模研究[J].計算機測量與控制，2016，24(1)：143-145.

[13] 雋志才，孫寶鳳.物流系統仿真[M].北京：電子工業出版社，2007：166-168.