WSN中DV-Hop節點定位算法的改進

任克強,李亞杰(江西理工大學信息工程學院,江西 贛州 341000)

?

WSN中DV-Hop節點定位算法的改進

任克強*,李亞杰
(江西理工大學信息工程學院,江西 贛州 341000)

為降低傳統DV-Hop算法對未知節點估算距離的誤差,提升WSN中的未知節點定位精度,提出一種基于未知節點估算距離修正的DV-Hop改進算法。該改進算法首先對節點的平均每跳距離進行修正,并根據節點分布和節點間鄰居關系的特點引入節點遠離度的概念,以區分未知節點和鄰居錨節點的距離,降低估算距離的誤差;然后對最小二乘法的誤差進行修正,并利用鄰居節點的通信范圍限制關系對未知節點估算坐標的誤差進行修正,以進一步減小未知節點的定位誤差。實驗結果表明,與傳統DV-Hop算法及相關文獻相比,改進算法可以有效減小未知節點估算距離的誤差,提升未知節點定位的精度。

無線傳感器網絡;節點定位;DV-Hop算法;估算距離;誤差修正

在無線傳感器網絡WSN(Wireless Sensor Network)中,許多應用都依賴傳感器的自我定位,如海水監測、交通控制、地質勘測、抗震救災等,這取決于準確獲取傳感器節點的位置信息[1]。獲取WSN中節點位置坐標的算法依據是否需要測量節點之間的相互距離可分類成基于測距和無需測距的定位算法[2];在低成本和低能耗等要求約束下,后者不依賴特殊硬件,相比于前者更具有優勢[3]。

DV-Hop定位算法是一種廣泛應用的無需測距定位算法,但當WSN中傳感器節點分布不均勻和不規則時,DV-Hop算法存在定位誤差較大的缺陷[4]。為了使定位的結果更加準確,相關研究者分別對其進行了不同程度的改進。文獻[5]通過引入距離矯正因子的概念以修正未知節點到錨節點的距離,使其更接近實際值,達到了減小定位誤差的目的。文獻[6]根據跳數閾值選擇合理的平均跳距來估計距離,同時利用質心算法和最小二乘法綜合估計定位坐標,有效改善了定位精度。文獻[7]采用多個節點通信半徑值進行多次節點信息廣播,精確了未知節點到錨節點的跳數信息,降低了定位誤差,但增加了節點間通信的開銷。文獻[8]將網絡中全部錨節點平均跳距最大值與最小值的平均值作為全網平均跳距,最后通過細菌覓食算法(BFO)來定位未知節點,有效地提高了傳感器節點分布不規則時的定位精度。文獻[9]通過距離三角不等式來約束多跳距離誤差,并采用加權雙曲線法來代替最小二乘法計算坐標,在一定程度上提升了定位準確度,但使用了額外的硬件設施。文獻[10]使用RSSI測距模型并對傳感器節點進行限跳處理,然后對錨節點優化組合,最后采用質心估算法定位未知節點坐標,在減小定位誤差的同時有效地減小了節點間通信信息量,但限跳會導致一些待定位節點因不能與錨節點通信而無法得到其位置坐標。文獻[11]通過對誤差距離加權與修正,選擇合理的跳段距離并使用遺傳算法計算未知節點位置,使定位結果更加準確。文獻[12]提出一種新的平均跳距求解方法,首先未知節點獲取所有鄰居錨節點的平均跳距,通過該跳距求出鄰居錨節點間相互距離并與實際值比較,引入百分比誤差作為加權系數的參考依據來計算未知節點的平均跳距,提高了定位性能。

針對傳統DV-Hop算法在隨機網絡中表現出的局限性,本文對其不合理的方面進行了分析研究和改進,提出一種基于未知節點估算距離修正的改進算法,使得節點間估算距離更接近實際值,以提升傳統DV-Hop算法的定位精度。

1 DV-Hop算法

DV-Hop算法主要包括以下3個步驟[13]:

①計算節點間最小跳數

相鄰節點間互相交換信息,使得網絡中所有節點均取得每個錨節點的坐標和與其間的最小跳數。

②計算節點間跳段距離

(1)

(2)

式中:Hopsizei為錨節點i的平均每跳距離,dij和hij分別為錨節點i、j之間的距離值和跳數,(xi,yi)和(xj,yj)分別為錨節點i、j的位置坐標。

錨節點將計算出的平均每跳距離作為校正值向網絡廣播,每一個未知節點只保留最先獲得的校正值,最后將校正值和到其他錨節點的跳數相乘得到該未知節點到其他錨節點的跳段距離。未知節點k和錨節點j之間的跳段距離dkj:

dkj=Hopsizei×hkj

(3)

式中:Hopsizei為k最先保留的校正值,hkj為k、j間的跳數。

③計算未知節點坐標

當待定位節點通過式(3)取得不少于3個跳段距離值時,其位置坐標可以通過極大似然估計法來求解。

如果待估算節點位置坐標為(x,y),到錨節點i的估計距離為di,(i=1,2,…,n),i的位置坐標為(xi,yi),(i=1,2,…,n),可得到方程組:

(4)

將式(4)中前(n-1)個等式分別與第n個等式相減可以得到AX=b形式的線性方程組,其中:

(5)

(6)

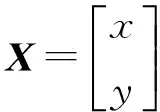
(7)

由最小二乘法,解得:

X=(ATA)-1ATb

(8)

2 DV-Hop算法分析與改進

DV-Hop算法定位過程中,未知節點與錨節點的距離并不是實際環境中兩點之間的距離,而是采用平均每跳距離與跳數相乘求出的跳段距離來估計的,平均每跳距離是根據錨節點的分布情況計算出的,因而導致在WSN節點分布不均勻和不規則時,必然存在較大的定位誤差。因此,本文從平均每跳距離、未知節點和錨節點的估算距離、最小二乘法引起的誤差以及未知節點定位坐標值誤差4個方面對DV-Hop算法進行了分析和修正改進。

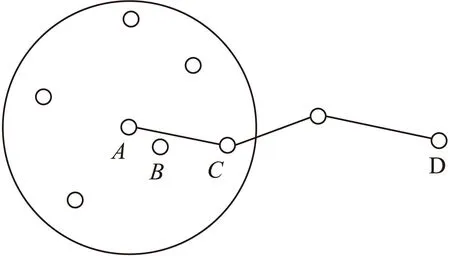
圖1 節點通信示意圖

2.1 平均每跳距離的修正

根據DV-Hop算法原理可知,為使得節點間跳數最小,節點在與相距較遠的節點通信時,會途經靠近通信范圍邊沿的節點。例如在圖1中,A、B、C和D分別為WSN中的4個傳感器節點,B、C均在A的最大通信半徑范圍內,為使得A與D之間通信時的跳數最小,A與D通信時則會途經更靠近通信范圍邊沿的C,而不經過B。

對于傳感器節點均勻分布的WSN環境,節點的一跳距離長度更接近于通信半徑的大小,由式⑴可知,平均跳距是由錨節點間實際距離總和除以其間跳數總和得出的,實際環境中節點隨機分布,若錨節點間相距過近,如圖1中節點A和B,則平均每跳距離值的計算誤差會偏大,進而影響定位效果。為減少因錨節點相距過近而引起的誤差,對由式⑵計算的dij進行以下修正:

(9)

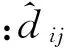
2.2 未知節點到錨節點距離的修正

在DV-Hop算法定位過程中,待定位節點與各個錨節點的估計距離是采取同一個平均跳距值乘以對應的跳數得出的結果,這樣會造成一定的誤差[14]。在圖1中,設節點B、C、D是錨節點,A是待定位節點,則A到B、C都是一跳,則根據式(3)計算出的A分別到B、C的距離是相等的,但實際上是不相等的,若按照相等的距離進行定位計算,顯然是不合理的,導致定位結果不準確。另一方面,假定A的平均跳距值是從B獲得的,大小為HopsizeB,若此值存在較大誤差,則A到其他錨節點的估算距離值的誤差會隨著跳數的增加而被累積,且HopsizeB無法代表整個網絡的分布情況;例如在圖1中,在估算A與D的距離時采用HopsizeB,顯然忽視了D周圍的分布情況。

①未知節點與鄰居錨節點距離的修正

為了區分不同未知節點與同一個鄰居錨節點的估計距離,本文引入節點遠離度的概念,用來表征未知節點與鄰居錨節點相離遠近的程度:

(10)

式中:εik為未知節點k與其鄰居錨節點i的遠離度,其值的大小和k、i間的距離正相關;Seti和Setk分別為i和k的鄰居節點標號集合,crad(Seti∪Setk)為Seti、Setk并集中所有元素個數,crad(Seti∩Setk)為Seti、Setk交集中所有元素個數。

下面用圖2舉例,說明節點遠離度的計算過程。A為錨節點;B、C分別為節點A單跳范圍內的未知節點;粗實線大圓、細實線大圓和虛線大圓分別為節點A、B和C的單跳通信范圍;空心小圓圈為其它傳感器節點。A和B的鄰居節點標號集合分別為SetA和SetB。可以算出,crad(SetA∪SetB)為21,crad(SetA∩SetB)為7,B與A的遠離度εAB=21/7=3,C與A的遠離度εAC=17/12≈1.42。遠離度εAB>εAC說明B和A相離更遠,兩者的距離更接近通信半徑,C和A相離更近。

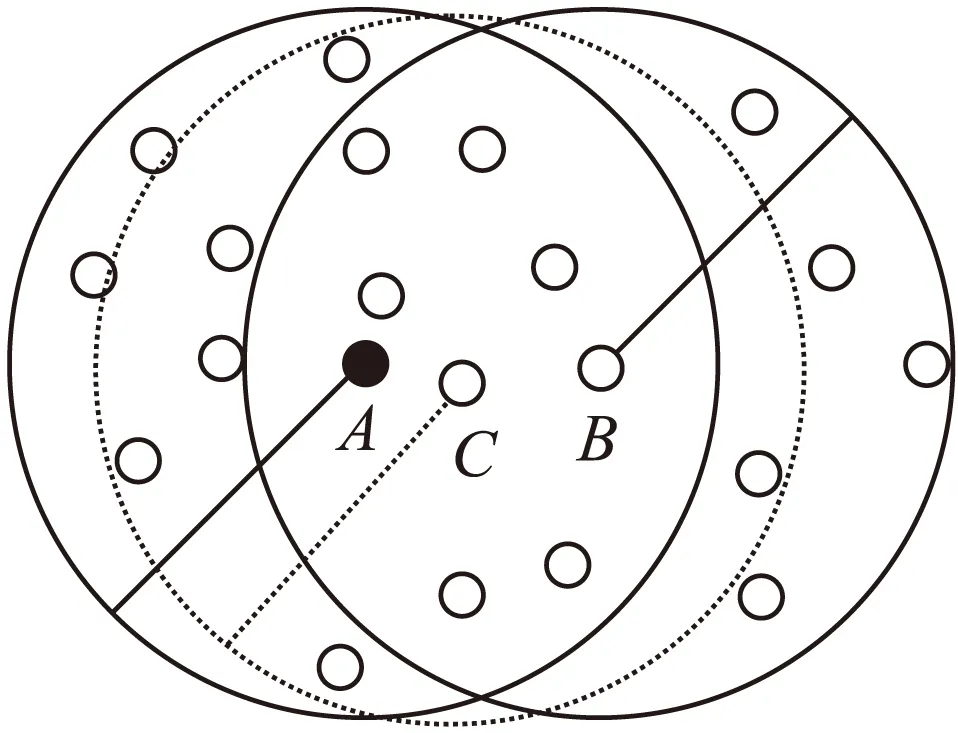
圖2 遠離度計算說明圖

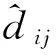
(11)

式中:εik為k與i的遠離度,εimax為i所有鄰居節點與i的遠離度最大值。

②未知節點與非鄰居錨節點距離的修正

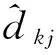
(12)

式中:Hopsizei為k在DV-Hop算法第2)步獲取的校正值,Hopsizej為j的平均跳距,hkj為k到j的跳數。

2.3 最小二乘法誤差的修正

在利用最小二乘法求解過程中,將式(4)中前(n-1)個等式分別與第n個等式相減可得出式(6),從而式(6)中每一項均包含dn,若dn的值誤差偏大,則必然給最后的定位結果帶來一定的誤差[15]。考慮到此過程中存在的問題,本文將式(4)中的n個等式重新按d1,d2,…,dn的值從大到小降序排列,使得第n個等式中dn的值最小,進而降低式(6)中向量b的誤差,然后按式⑻求解得出定位坐標。

為了便于分析比較,本文將通過以上改進后的DV-Hop算法稱為本文算法1。

2.4 未知節點坐標值誤差的修正

未知節點由本文算法1計算得出的坐標X′與實際坐標X相比仍然存在一定誤差,此誤差體現在未知節點和錨節點的距離上,例如X′與X分別和每個錨節點相距遠近程度是有差異的。為簡化計算量,只考慮跳數是否為1的差異,即節點是否為鄰居關系的差異,實際中節點應滿足要求:對于具有鄰居關系的兩個節點,節點間距離不超過通信半徑,相反,對于不具有鄰居關系的兩個節點,節點間距離大于通信半徑[16],所以對X′為滿足實際情況進行修正。

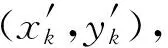
(13)

(14)

(15)

式中:(xj,yj)(j=1,2,…,n)為錨節點坐標,Lx和Ly分別為網絡區域橫坐標和縱坐標的最大值,對式⒂求解得到最后的修正位置坐標,稱為本文算法2。

未知節點k誤差修正的流程如圖3所示。

下面以圖4為例,說明未知節點k誤差的修正過程。圖中節點1、2、3和4均代表參與k定位計算的錨節點,空心小圓代表k的真實位置,空心三角為本文算法1定位得出的估算位置,用k1表示,由式(13)可得,Dk=(-1,-1,1,1),-1表示k1和錨節點1、2不為鄰居關系,1表示k1和錨節點3、4為鄰居關系。由式(14)可得,Hk=(-1,1,-1,1),表示k實際位置和錨節點1、3不為鄰居關系,和錨節點2、4為鄰居關系。Dk≠Hk表明估算位置k1不夠準確,與實際位置存在誤差,應使其為滿足Hk所表示的關系進行修正,即與錨節點1保持非鄰居關系不變,與錨節點4保持鄰居關系不變,同時離開錨節點3使它們不為鄰居關系,接近錨節點2使它們為鄰居關系。滿足條件修正距離最小的點為圖中空心方框位置k2,即通過式(15)的計算會將k1位置坐標修正到k2位置,達到減小定位誤差的目的。

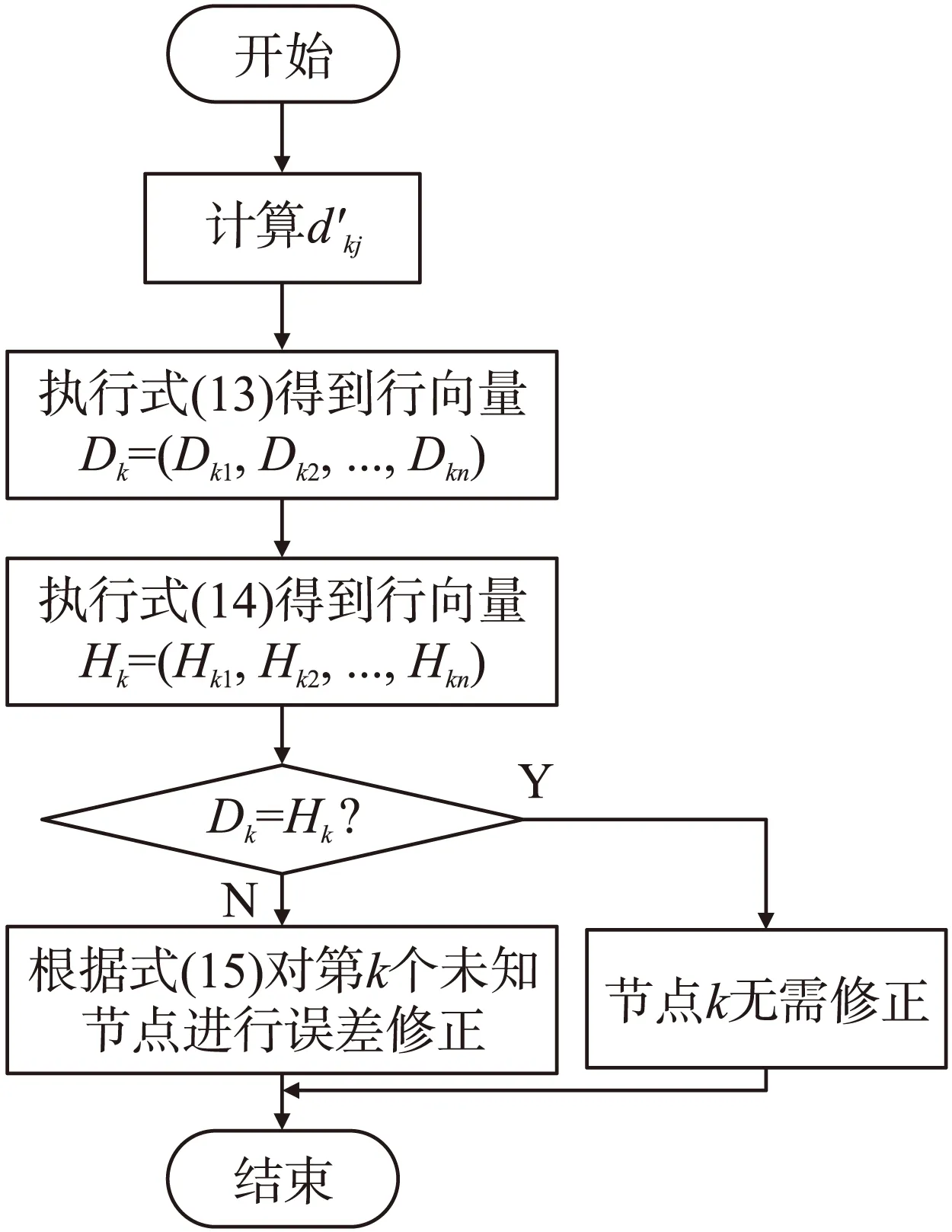
圖3 未知節點k坐標修正流程圖

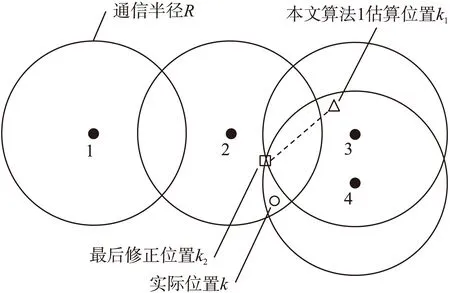
圖4 未知節點k坐標修正舉例

3 實驗結果與分析

使用MATLABR2015b工具對DV-Hop算法、文獻[11]算法、本文算法1和本文算法2進行實驗仿真,并對實驗結果進行對比和分析。實驗仿真環境:在100m×100m的WSN環境中任意安放100個節點,包括錨節點和未知節點,且錨節點數量+未知節點數量=100,節點通信半徑為R。

評價定位效果的標準為平均定位誤差error和相對定位誤差aerror:

(16)

aerror=error/R

(17)

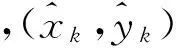
圖5是通信半徑R=30m和R=35m時錨節點數目的變化對4種算法平均定位誤差影響的實驗結果。從結果可以看到,4種算法在錨節點數量依次遞增且通信半徑不變的情況下,平均定位誤差都表現為遞減變化,剛開始下降幅度較大,以后下降逐漸趨于緩慢。本文算法1平均定位誤差在錨節點數量為5時和文獻[11]算法接近,以后隨著錨節點數量的增多均優于文獻[11]算法;本文算法2是對本文算法1坐標誤差修正的結果,從圖5中可以看到達到了進一步減小誤差的效果。圖5(a)中錨節點數量為40時,本文算法2平均定位誤差相比文獻[11]算法和DV-Hop算法分別下降約2.7m和5.4m;通過圖5(a)與圖5(b)對比可以觀察到,錨節點數量相同情況下,通信半徑從30m變大為35m會使4種算法的平均定位誤差都略有提升,原因在于通信半徑增大使得錨節點平均跳距增大,進而使未知節點到錨節點的估計距離和實際值偏差變大,影響定位效果;但隨著錨節點數量的增多,通信半徑增大對本文兩種算法的影響較小。

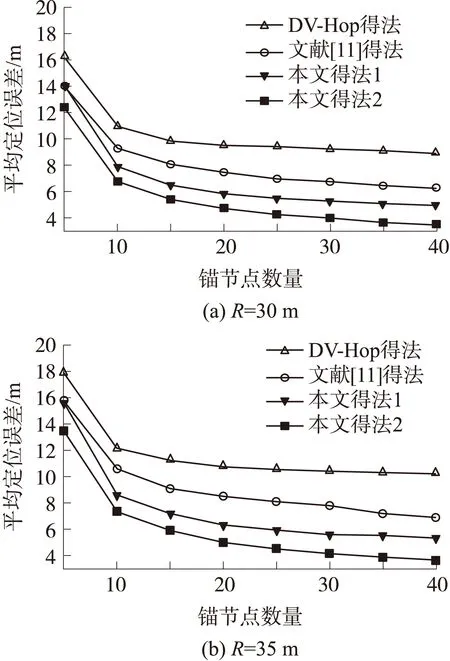
圖5 不同錨節點數量的平均定位誤差比較

圖6是通信半徑R=30m、R=35m和R=40m時錨節點數量的變化對4種算法相對定位誤差影響的實驗結果。從結果可以看到,在通信半徑不變的情況下,4種算法的相對定位誤差和圖5變化趨勢一致,都表現為先快速下降而后緩慢下降。在錨節點數量為5情況下本文算法1的相對定位誤差與文獻[11]算法差別比較小,以后隨著錨節點數量遞增均優于文獻[11]算法和DV-Hop算法。圖6(a)中本文算法2的定位性能相比文獻[11]算法和DV-Hop算法分別提升5.0%～9.7%和12.8%～18.6%;由圖6(a)、圖6(b)和圖6(c)對比可以看到,錨節點數量相同條件下,通信半徑增大會使4種算法相對定位誤差都表現出小幅度下降,這是因為通過式(17)計算平均相對誤差時,通信半徑在分母,使得計算結果偏小。

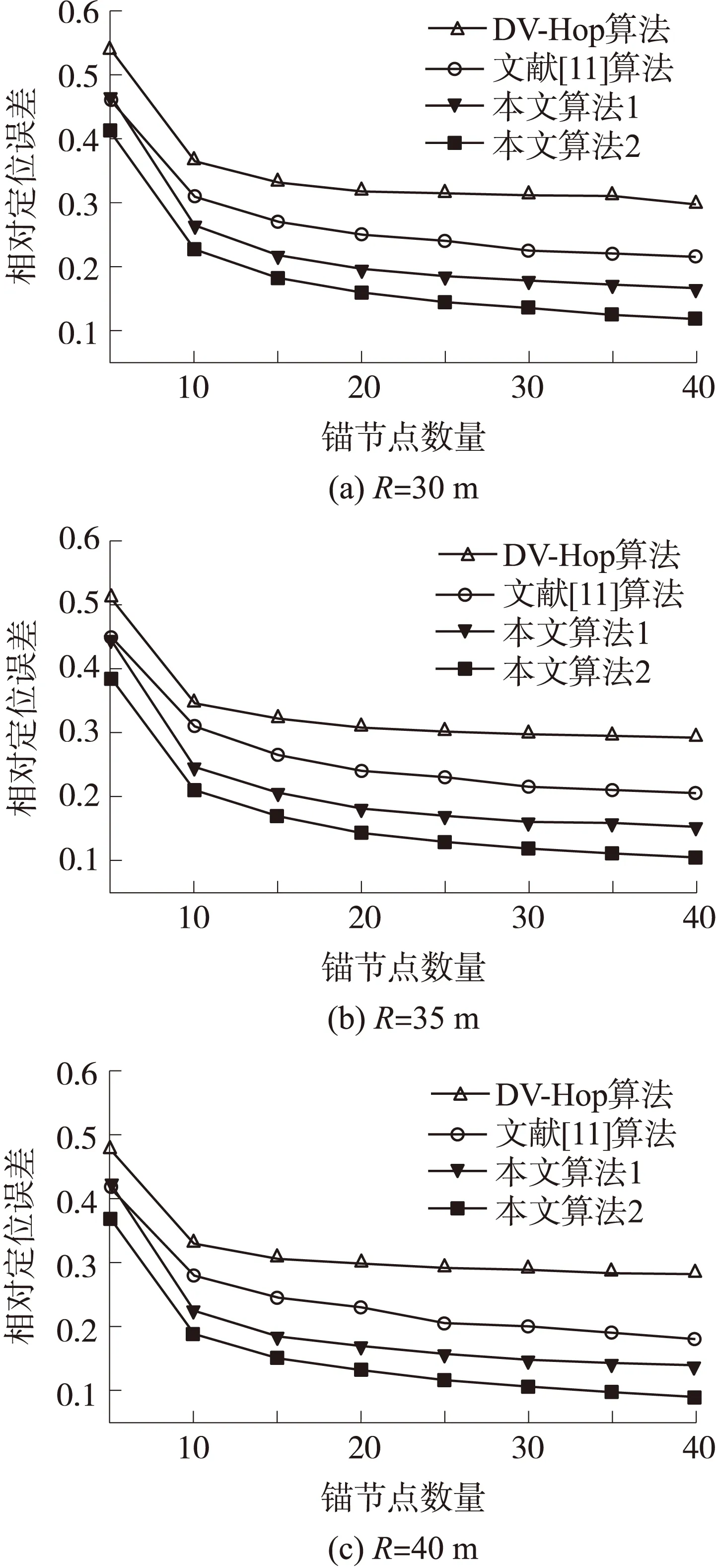
圖6 不同錨節點數量的相對定位誤差比較

圖5和圖6表明本文算法的定位性能優于文獻[11]算法和DV-Hop算法,這是由于本文通過計算遠離度對未知節點到錨節點的距離進行修正,并依據節點鄰居關系對估算坐標值進一步修正,使其更接近實際值,相比于文獻[11]算法和DV-Hop算法,本文算法的定位性能得到了有效提升。

圖7是通信半徑R=40m、錨節點數量n=25時DV-Hop算法和本文算法2的每個未知節點的定位誤差。從圖7中可以看到,兩者定位誤差差距較大,DV-Hop算法在11.5m左右波動,而本文算法2在4.5m左右波動,且有30.7%節點的定位誤差在3m以內;因此,本文算法2不僅減小了定位誤差,且穩定性也得到較好地提升。

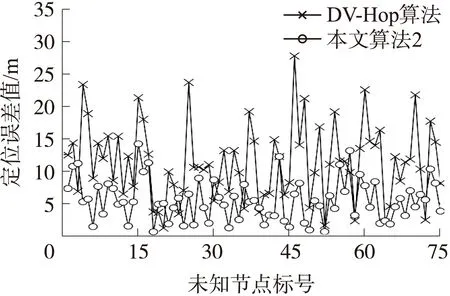
圖7 未知節點的定位誤差比較圖

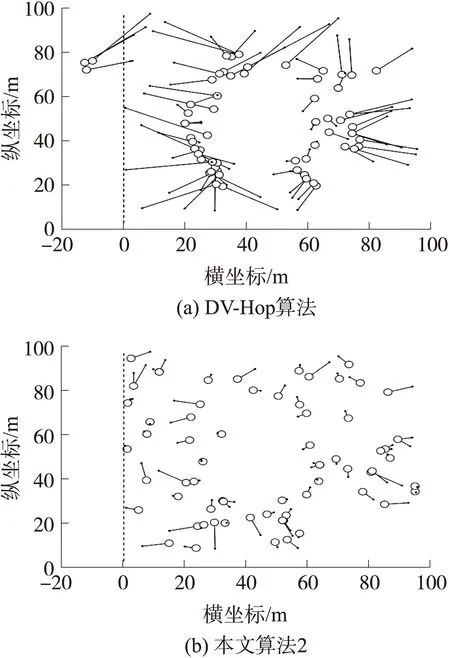
圖8 未知節點的實際位置與定位位置比較

圖8是R=50m、錨節點數量n=30時DV-Hop算法和本文算法2的每個未知節點的定位位置和實際位置,圖中黑色小圓點表示實際坐標位置,空心小圓表示定位估計坐標位置,且圖8(a)與圖8(b)中黑色小圓點坐標位置相同。從圖8(a)中可以看到,DV-Hop算法存在一部分節點的估計坐標位置超出了WSN節點部署區域范圍的情況,這使得這些節點的估計坐標位置和實際位置距離相差過大,造成平均定位誤差偏大的結果;而從圖8(b)中可以看到,本文算法2不存在節點的定位位置超出WSN節點布署區域范圍的情況,這是由于式(15)的約束作用,保證了所有節點的定位位置均在WSN節點部署區域范圍內,而且相比DV-Hop算法顯著提升了總體定位效果。

4 結束語

針對在隨機分布網絡環境中傳統DV-Hop算法的局限性,對引起定位誤差的來源進行研究和分析,提出一種改進的DV-Hop算法。改進算法從錨節點平均每跳距離的計算、未知節點到錨節點距離的計算、最小二乘法求解未知節點坐標以及坐標修正4個方面對傳統DV-Hop算法進行了改進,并在不同錨節點數量和不同節點通信半徑的WSN環境下進行了算法定位性能比較實驗。實驗結果表明,本文改進算法的平均定位誤差和相對定位誤差均優于傳統DV-Hop算法及相關文獻,有效提升了DV-Hop算法的節點定位性能。如何進一步減小未知節點定位位置與實際位置的誤差是后續研究的重點工作。

[1] Xu C X,Chen J Y. Research on the Improved DV-Hop Localization Algorithm in WSN[J]. International Journal of Smart Home,2015,9(4):157-162.

[2] Safa H. A Novel Localization Algorithm for Large Scale Wireless Sensor Networks[J]. Computer Communications,2014,45(3):32-46.

[3] 曹欲曉,嚴奎,徐金寶. 一種最優錨節點集合上的兩重粒子群優化DV-Hop定位算法[J]. 傳感技術學報,2015,28(3):424-429.

[4] Fang X. Improved DV-Hop Positioning Algorithm Based on Compensation Coefficient[J]. Journal of Software Engineering,2015,9(3):650-657.

[5] Wu L,Hou Z,Tan C,et al. Improved DV-Hop Localization Algorithm Based on Distance Correction of Anchor Nodes[J]. International Journal of Future Generation Communication and Networking,2016,9(10):269-278.

[6] 向滿天,王勝,楊友華. 基于閾值機制與距離校正的WSN改進DV-Hop定位算法[J]. 傳感技術學報,2016,29(6):920-926.

[7] 劉士興,黃俊杰,劉宏銀,等. 基于多通信半徑的加權DV-Hop定位算法[J]. 傳感技術學報,2015,28(6):883-887.

[8] Zhao Q S,Hu Y L. An Improved DV-Hop Localisation Algorithm[J]. International Journal of Wireless and Mobile Computing,2016,10(1):20-25.

[9] 周玲,康志偉,何怡剛. 基于三角不等式的加權雙曲線定位DV-Hop算法[J]. 電子測量與儀器學報,2013,27(5):389-395.

[10] 夏少波,鄒建梅,朱曉麗,等. 基于跳數區域劃分的DV-Hop改進算法[J]. 傳感技術學報,2014,27(7):964-969.

[11] 程超,錢志鴻,付彩欣,等. 一種基于誤差距離加權與跳段算法選擇的遺傳優化DV-Hop定位算法[J]. 電子與信息學報,2015,37(10):2418-2423.

[12] Wang Y,Fang Z,Chen L. A New Type of Weighted DV-Hop Algorithm Based on Correction Factor in WSNs[J]. Journal of Communications,2014,9(9):699-705.

[13] Zhang W,Yang X,Song Q. DV-Hop Localization Algorithm Based on RSSI Correction[J]. Journal of Software Engineering,2015,9(1):188-194.

[14] Zhang J,Guo N,Li J. An Improved DV-Hop Localization Algorithm Based on the Node Deployment in Wireless Sensor Networks[J]. International Journal of Smart Home,2015,9(10):197-204.

[15] 朱敏,劉昊霖,張志宏,等. 一種基于DV-Hop改進的無線傳感器網絡定位算法[J]. 四川大學學報(工程科學版),2012,44(1):93-98.

[16] Shang F,Lan L,Dong M. Position Location Scheme Using Nonlinear Programming Based on RSSI and DV-Hop[J]. International Journal of Hybrid Information Technology,2015,8(5):1-10.

任克強(1959-),男,教授,碩士研究生導師,主要研究方向為圖像與視頻處理、無線傳感器網絡、信息隱藏,jxrenkeqiang@163.com;

李亞杰(1992-),男,碩士研究生,主要研究方向為無線傳感器網絡。

Improvement of DV-Hop Node Localization Algorithm in WSN

REN Keqiang*,LI Yajie
(School of Information Engineering,Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000,China)

In order to reduce the estimation error of the traditional DV-Hop algorithm,an improved DV-Hop algorithm based on modification of estimation distance was proposed to enhance the localization accuracy of unknown nodes in WSN. Firstly,the improved algorithm modified average distance per hop for nodes,and degree of distance among notes was introduced according to the nodes distribution and the characteristics of neighbor relation between nodes,so as to distinguish the distance between unknown nodes and anchor nodes,and to reduce the error of the estimation distance. Then,the error of the least squares method was modified,and the constraint relationships of communication range between neighbor nodes were utilized to modify the error of the estimation coordinates for unknown nodes,which could further reduce the error of locating unknown nodes. The experimental results show that compared with the traditional DV-Hop algorithm and the related reference,the improved algorithm can effectively reduce the error of the estimation distance for unknown nodes,and improve the localization accuracy of unknown nodes.

wireless sensor network;node localization;DV-Hop algorithm;estimation distance;error modification

2016-07-26 修改日期:2016-12-05

TP393

A

1004-1699(2017)04-0611-07

C:6150P

10.3969/j.issn.1004-1699.2017.04.022