弱entwining結構的cup積

史 美 華

(浙江外國語學院， 浙江 杭州 310012)

弱entwining結構的cup積

史 美 華

(浙江外國語學院， 浙江 杭州 310012)

給出了弱entwining結構上同調的2種cup積，并證明了它們都是求導度為1的分次結合代數，同時證明了弱entwining結構的復形是弱comp代數，利用其結論得到了2種cup積結構的關系，推廣了雙代數的Gerstenhaber-Schack理論.

弱entwining結構；弱comp代數；cup積

本文首先給出了弱entwining結構上同調的2種cup積，并證明其均勻求導度為1的分次結合代數.其次，證明了弱entwining結構的復形是弱comp代數，并利用其結論得到了2種cup積結構的關系，從而推廣了雙代數的Gerstenhaber-Schack理論.

由文獻[3]知，一個域k上的弱entwining結構(A,C,ψ)是由代數A、余代數C和k-線性映射ψ:C?A→A?C,c?a→∑aψ?cψ組成，并且對?a,b∈A,c∈C滿足：

∑(ab)ψ?cψ=∑aψbφ?cψφ;

(1)

∑aψ?cψ1?cψ2=∑aψφ?c1φ?c2ψ;

(2)

∑1ψ?cψ=∑1ψε(c1ψ)?c2;

(3)

∑aψε(cψ)=∑1ψaε(cψ).

(4)

當一個弱entwining映射ψ在同一個式子中多次出現時，分別用符號ψ1,ψ2,...,δ,θ,...等表示.若1ψ?cψ=1?c，則弱entwining結構就是entwining結構.

(5)

(6)

(7)

(8)

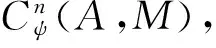
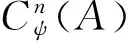
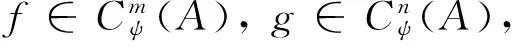
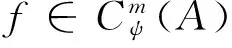
∑1ψf(cψ2?a1?…?am)φ×

g(cψ1φ?am+1?…?am+n)=

∑1ψδf(c2ψ?a1?…?am)φ×

g(c1δφ?am+1?…?am+n);

∑1ψ(1δf(cψ2δ?a1?…?am))φ×

g(cψ1φ?am+1?…?am+n)=

∑1ψ1δθf(cψ2δ?a1?…?am)φ×

g(cψ1θφ?am+1?…?am+n)=

∑1ψ?1δθf(c2ψδ?a1?…?am)φ×

g(c1?θφ?am+1?…?am+n)=

∑(1ψ1δ)θf(c2ψδ?a1?…?am)φ×

g(c1θφ?am+1?…?am+n)=

∑1ψθf(c2ψ?a1?…?am)φ×

g(c1θφ?am+1?…?am+n);

∑1ψf(cψ2?a1?…?am)φ1δ×

g(cψ1φδ?am+1?…?am+n)=

∑1ψf(cψ2?a1?…?am)φ×

g(cψ1φ?am+1?…?am+n)=

∑1ψθf(c2ψ?a1?…?am)φ×

∑(f(c3?a1?…?am)δ×

g(c2δ?am+1?…?am+n))φ×

h(c1φ?am+n+1?…?am+n+l)=

∑f(c3?a1?…?am)δφ×

g(c2δ?am+1?…?am+n)ψ×

h(c1φψ?am+n+1?…?am+n+l)=

(c1δ?am+1?…?am+n+l)=

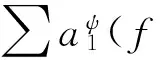
a1?…?am+n)am+n+1=

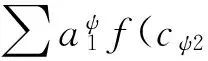
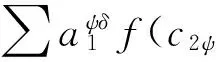
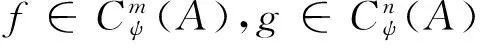
顯然，定義1中的式(6)成立.

∑f(c1?a1φ1ψ1?…?aiφiψi?g(c2ψ1...ψi?ai+1φi+1?…?ajφj?h(c3φ1...φj?aj+i?…?aj+l)?an+l+i-1)?an+l+i?…?am+n+l-2);

∑f(c1?a1φ1?…?aiφi?g(c2φ1...φi1?ai+1φi+1?…?ajφj?h(c2φ1...φi2φi+1...φj?aj+i?…?aj+l)?an+l+i-1)?an+l+i?…?am+n+l-2)=

∑f(c1?a1φ1ψ1?…?aiφiψi?g(c2ψ1...ψi?ai+1φi+1?…?ajφj?h(c3φ1...φj?aj+i?…?aj+l)?an+l+i-1)?an+l+i?…?am+n+l-2),

因此，式(7)成立.

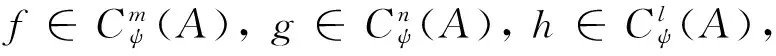
∑ε(c3φ1...φjδ)f(c1?a1φ1ψ1?…?ajφjψj?(1δaj+1aj+2)ψj+1?aj+3ψj+3?…?ai+1ψi+1?g(c2ψ1...ψi+1?ai+2?…?an+i+1)?an+i+2?am+n)=

∑f(c1?a1φ1?…?ajφj?1δaj+1ψj+1aj+2ψj+2?aj+3ψj+3?…?ai+1ψi+1?g(c2φ1...φjδψj+1...ψi+1?ai+2?…?an+i+1)?an+i+2?am+n);

∑f(c1?a1φ1ψ1?…?ajφjψj?π(c2ψ1...ψj?aj+1φj+1?aj+2φj+2)?g(c3φ1...φi+1?ai+2?…?an+i+1)?an+i+2?…?am+n)=

∑ε(c2φ1...φj1δ)f(c1?a1φ1?…?ajφj?1δaj+1φj+1aj+2φj+2?g(c2φ1...φj2φj+1...φi+1?ai+2?…?an+i+1)?an+i+2?…?am+n)=

∑f(c1?a1φ1?…?ajφj?1δaj+1ψj+1aj+2ψj+2?aj+3ψj+3?…?ai+1ψi+1?g(c2φ1...φjδψj+1...ψi+1?ai+2?…?an+i+1)?an+i+2?am+n),

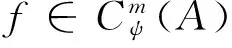
由定理1，直接可得本文的一個主要結論，同時也是雙代數Gerstenhaber-Schack理論[6-7]中經典結論的推廣.

由推論1可得

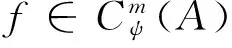
(δm+n(δm(f)∝g))(c?a1?…?am+n)=

∑1φ1ψf(cφ1ψ?a1ψ1?…?amψm)g(cφ2ψ1...ψm?am+1?…?am+n)=

∑1φδ1ψf(c1δψ?a1ψ1?…?amψm)g(c2φψ1...ψm?am+1?…?am+n)=

∑1φψf(c1ψ?a1ψ1?…?amψm)g(c2φψ1...ψm?am+1?…?am+n)=

∑1φf(cφ1?a1ψ1?…?amψm)g(cφ2ψ1...ψm?am+1?…?am+n)=

δm+n(f∝g)(c?a1?…?am+n);

δm+n(f∝δn(g))(c?a1?…?am+n)=

∑1φf(cφ1?a1ψ1?…?amψm)1δg(cφ2ψ1...ψmδ?am+1?…?am+n)=

∑1φf(cφ1?a1ψ1?…?amψm)(1·g)(cφ2ψ1...ψm?am+1?…?am+n)=

∑1φf(cφ1?a1ψ1?…?amψm)g(cφ2ψ1...ψm?am+1?…?am+n)=

δm+n(f∝g)(c?a1?…?am+n),

因此，δm+n(f∝g)=δm+n(f∝δn(g))=δm+n(δm(f)∝g).

(f∝(g∝h))(c?a1?…?am+n+l)=

∑f(c1?a1ψ1?…?amψm)(g∝h)(c2ψ1...ψm?am+1?…?am+n+l)=

∑f(c1?a1ψ1?…?amψm)g(c2ψ1...ψm1?am+1φ1?…?am+nφn)h(c2ψ1...ψm2φ1...φn?am+n+1?…?am+n+l)=

∑f(c1?a1ψ1δ1?…?amψmδm)g(c2δ1...δm?am+1φ1?…?am+nφn)h(c3ψ1...ψmφ1...φn?am+n+1?…?am+n+l)=∑(f∝g)(c1?a1ψ1?…?am+nψm+n)h(c2ψ1...ψm+n?am+n+1?…?am+n+l)=

((f∝g)∝h)(c?a1?…?am+n+l),

這里，反復利用了式(2).

(df∝g)(c?a1?…?am+n+1)=

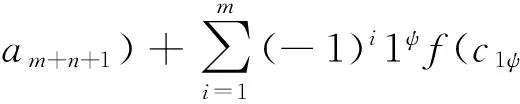
(-1)m(f∝dg)(c?a1?…?am+n+1)=

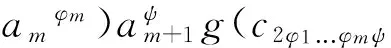
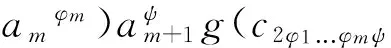
d(f∝g)(c?a1?…?am+n+1)=

…?amδm)g(c2ζδ1...δm?am+1?…?aiai+1?…?am+n+1)+(-1)m+n+11?σf(c1σ?a1δ1?…?amδm)g(c2?δ1...δm?am+1?…?am+n)am+n+1=

這里，反復利用了式(2)和(3).于是d(f∝g)=df∝g+(-1)mf∝dg.定理4證畢.

[1]BRZEZISKIT,MAJIDS.Coalgebrabundles[J]. Comm Math Phys,1998,191(2):517-522.

[3] CAENEPEEL S, GROOT E D. Modules over weak entwining structures[J]. Contemp Math,2000,267:31-54.

[4] 賈玲,李方.弱entwining結構的上同調[J].中國科學A輯:數學,2007,37(1):55-63. JIA L, LI F. Weak entwining structure of cohomology[J]. Science in China: Ser A,2007,37(1):55-63.

[5] 賈玲,李方.弱entwined模的Frobenius性質和Maschke型定理[J].數學學報,2007,50(1):105-117. JIA L, LI F. Frobenius properties and Maschke type theorems for weak entwining modules[J].Acta Mathematica Sinica,2007,50(1):105-117.

[6] GERSTENHABER M. The cohomology structure of an associative ring[J]. Ann Math,1964,79:59-103.

[7] GERSTENHABER M, SCHACK S D. Bialgebra cohomology, deformations and quantum group[J]. Procl Natl Acad Sci,1990,87:478-481.

SHI Meihua

(ZhejiangInternationalStudiesUniversity,Hangzhou310012,China)

This paper introduces two kinds of cup products of the homological over a weak entwining structure, and proves that they are both graded associative algebras of degree 1. Then, we state that complexes of weak entwining structures are weak comp algebras, which obtains the relations of the two cup products. And, the classical Gerstenhaber-Schack theory is extended.

weak entwining structure; weak comp algebra; cup product

2014-10-12.

史美華(1963-)，ORCID:http://orcid.org/0000-0002-6151-2494，女，教授，主要從事Hopf代數研究,E-mail,shimeihua63@163.com.

10.3785/j.issn.1008-9497.2017.02.003

O 153

A

1008-9497(2017)02-139-05

The cup products of a weak entwining structure. Journal of Zhejiang University(Science Edition), 2017,44(2):139-143