含無(wú)關(guān)項(xiàng)布爾函數(shù)的對(duì)稱變量檢測(cè)算法
張永波,厲曉華
(1.浙江旅游職業(yè)學(xué)院 信息中心, 浙江 杭州 311231; 2.浙江大學(xué) 信息中心, 浙江 杭州 310027)
含無(wú)關(guān)項(xiàng)布爾函數(shù)的對(duì)稱變量檢測(cè)算法
張永波1,厲曉華2*
(1.浙江旅游職業(yè)學(xué)院 信息中心, 浙江 杭州 311231; 2.浙江大學(xué) 信息中心, 浙江 杭州 310027)
為簡(jiǎn)化布爾函數(shù)中12類對(duì)稱變量的檢測(cè)過(guò)程,提出了含無(wú)關(guān)項(xiàng)布爾函數(shù)基于最小項(xiàng)展開(kāi)系數(shù)的對(duì)稱變量檢測(cè)算法. 該算法通過(guò)判別布爾函數(shù)有序特征值矩陣的約束條件以實(shí)現(xiàn)對(duì)稱變量的快速檢測(cè). 應(yīng)用結(jié)果表明,與現(xiàn)有方法相比,算法在適用的布爾函數(shù)變量數(shù)、檢測(cè)類型、檢測(cè)含無(wú)關(guān)項(xiàng)布爾函數(shù)和檢測(cè)過(guò)程的復(fù)雜度方面表現(xiàn)較優(yōu).
對(duì)稱變量;有序特征值矩陣;布爾函數(shù);真值表;任意項(xiàng)
0 引 言
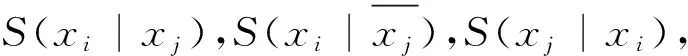
1 布爾函數(shù)最小項(xiàng)展開(kāi)式
任意n變量含無(wú)關(guān)項(xiàng)布爾函數(shù)的最小項(xiàng)展開(kāi)式表示為[6]:
(1)
di∈{0,1}表示無(wú)關(guān)項(xiàng)系數(shù),di=0表示mi不屬于無(wú)關(guān)項(xiàng),di=1表示mi屬于無(wú)關(guān)項(xiàng),di,mi不同時(shí)為1.
2 對(duì)稱變量檢測(cè)方法
2.1 相關(guān)定義
根據(jù)文獻(xiàn)[7],布爾函數(shù)存在6類對(duì)稱變量和6類反對(duì)稱變量,其定義如表1和2所示.
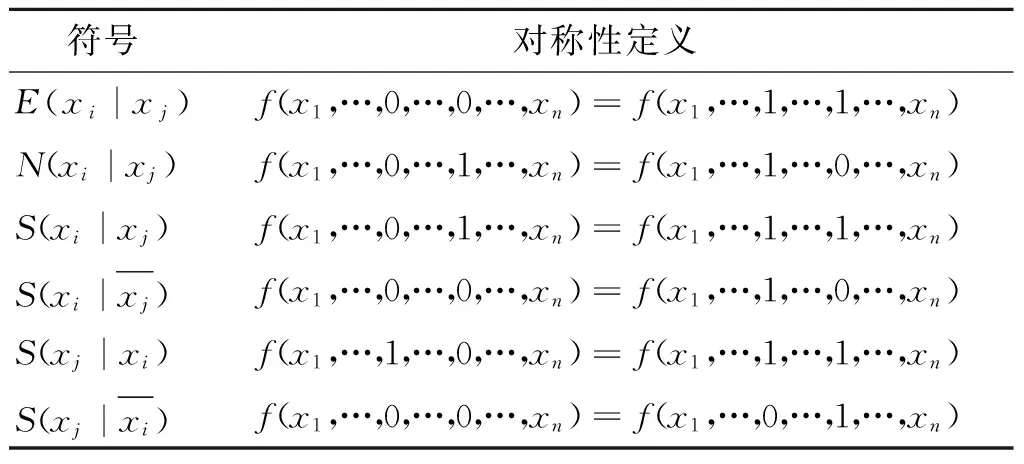
表1 6類對(duì)稱變量Table 1 Six types of symmetry

表2 6類反對(duì)稱變量Table 2 Six types of antisymmetry
定義1 最小項(xiàng)展開(kāi)系數(shù)矩陣
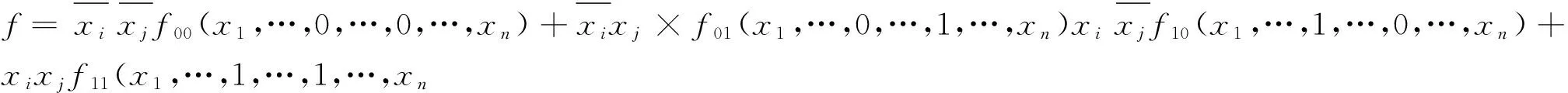
若將展開(kāi)式中子函數(shù)f00(x1,…,0,…,0,…,xn),f01(x1,…,0,…,1,…,xn),f10(x1,…,1,…,0,…,xn),f11(x1,…,1,…,1,…,xn)的最小項(xiàng)展開(kāi)系數(shù)ai按下標(biāo)i升序排列組成有序矩陣,該有序矩陣稱為子函數(shù)的最小項(xiàng)展開(kāi)系數(shù)矩陣,分別表示為C0,C1,C2,C3.
定義2 當(dāng)邏輯變量xixj取值00,01,10,11時(shí),布爾函數(shù)真值表中的相應(yīng)最小項(xiàng)展開(kāi)系數(shù)稱為真值表的特征值.
定義3 當(dāng)邏輯變量xixj取00,01,10,11不同值時(shí),該變量編碼稱為xixj的特征編碼.
定義4 若將真值表的特征值ai按下標(biāo)i升序排列組成有序矩陣,則該矩陣稱為有序特征值矩陣,表示為[ai]xixj. 當(dāng)邏輯變量xixj取值00,01,10,11時(shí),[ai]xixj可表示為[ai]00,[ai]01,[ai]10,[ai]11.
由定義1~3可知,C0,C1,C2,C3和[ai]xixj滿足如下關(guān)系:
C0=[ai]00,C1=[ai]01,C2=[ai]10,C3=[ai]11.
定義5 矩陣A、B異或運(yùn)算就是對(duì)2個(gè)矩陣中的相應(yīng)元素進(jìn)行異或操作.
若A=[a1…ai…an],B=[b1…bi…bn],
則A⊕B=[a1⊕b1…ai⊕bi…an⊕bn].
定義6 在有序特征值矩陣中,除無(wú)關(guān)項(xiàng)之外的所有元素均稱為決定性元素.
2.2 算法原理
定理1 若n變量布爾函數(shù)f(x1,…,xi,…,xj,…xn)的有序特征值矩陣[ai]xixj中的決定性元素異或運(yùn)算結(jié)果滿足表3的約束條件,則該布爾函數(shù)存在相應(yīng)的對(duì)稱變量.
證明 以[ai]xixj約束條件[ai]00⊕[ai]11=[000…0]為例,根據(jù)異或運(yùn)算的性質(zhì),無(wú)關(guān)性與0、1、無(wú)關(guān)項(xiàng)之間的異或運(yùn)算結(jié)果如表4所示. 矩陣[ai]00、[ai]11進(jìn)行異或運(yùn)算時(shí),只需考慮決定性元素.
若n變量布爾函數(shù)f(x1,…,xi,…,xj,…xn)的有序特征值矩陣[ai]xixj滿足[ai]00⊕[ai]11=[000…0],則有
C0⊕C3=[000…0].
(2)
式(2)可改寫為:
C0⊕C3⊕C3=[000…0]⊕C3,
C0⊕(C3⊕C3)=C3,
C0⊕[000…0]=C3,
C0=C3,
所以f(x1,…,0,…,0,…,xn)=f(x1,…,1,…,1,…,xn). 由表1的定義可知,該布爾函數(shù)存在E(xi|xj)類對(duì)稱變量.
同理,可證得表3中其他11類對(duì)稱變量.

表3 邏輯變量對(duì)稱條件Table 3 The symmetric conditions of logical variables
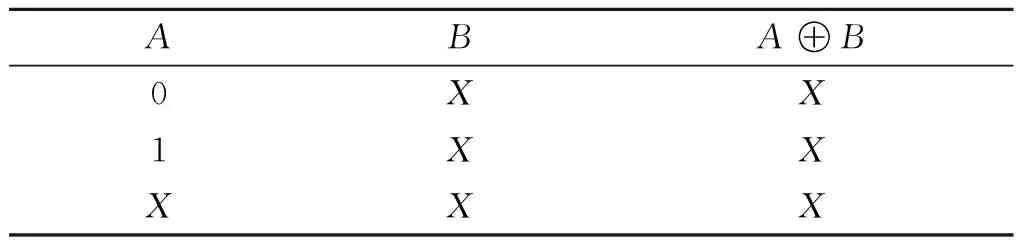
表4 異或運(yùn)算Table 4 The exclusive operation
由上述討論可知,基于有序特征值矩陣檢測(cè)含無(wú)關(guān)項(xiàng)布爾函數(shù)12類對(duì)稱變量的過(guò)程如下:
(1)列出布爾函數(shù)的真值表.
(2)根據(jù)真值表得到[ai]xixj.
(3)對(duì)[ai]xixj中的無(wú)關(guān)項(xiàng)元素略去異或運(yùn)算,判斷[ai]xixj是否滿足表3的元素條件.
2.3 算法實(shí)例
例1 三變量布爾函數(shù)f1(x1,x2,x3)=∑m(0,2,5,6)+d(7),應(yīng)用有序特征值矩陣方法檢測(cè)對(duì)稱變量.
由函數(shù)f1(x1,x2,x3)的真值表(見(jiàn)表5)可得[ai]x1x2:
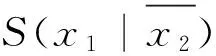
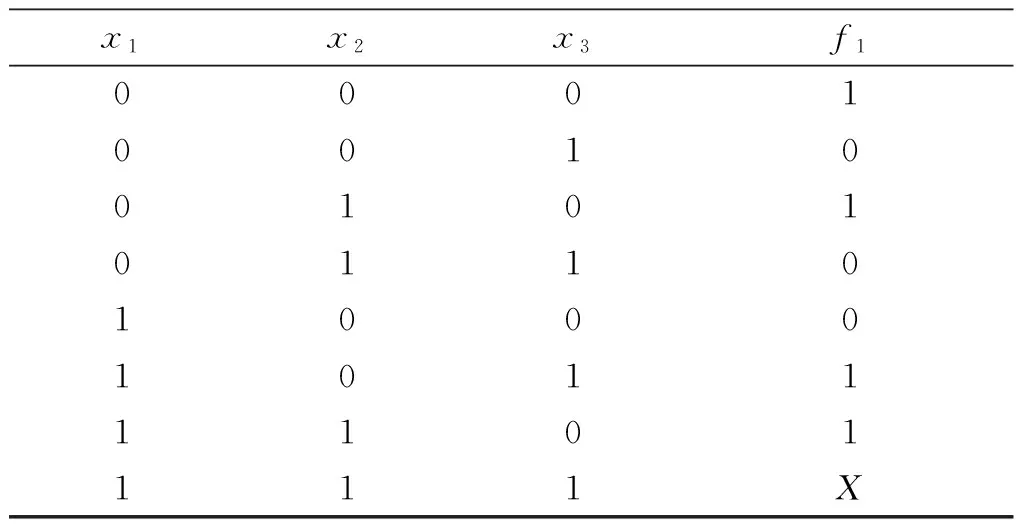
表5 布爾函數(shù)f1的真值表Table 5 The truth table of f1

2.4 算法實(shí)現(xiàn)
步驟1 定義二維數(shù)組y,用于保存被檢測(cè)函數(shù). 數(shù)組y存在2n行和n+1列. 前n行保存f(x1~xn)的變量編碼,最后一行保存被檢測(cè)函數(shù)的最小項(xiàng)展開(kāi)系數(shù). 以本文2.3節(jié)中的例1為例,得到的二維數(shù)組y1如表6所示.

表6 二維數(shù)組y1Table 6 Representation of columns of array y1
步驟2 定義一維數(shù)組C0,C1,C2,C3. 任意選擇數(shù)組y中的兩列,即邏輯變量xi、xj(1≤i (1)若y[k][i]=0,y[k][j]=0,則將y[k][n+1]的值保存于數(shù)組C0. (2)若y[k][i]=0,y[k][j]=1,則將y[k][n+1]的值保存于數(shù)組C1. (3)若y[k][i]=1,y[k][j]=0,則將y[k][n+1]的值保存于數(shù)組C2. (4)若y[k][i]=1,y[k][j]=1,則將y[k][n+1]的值保存于數(shù)組C3. 步驟3 判斷數(shù)組C0,C1,C2,C3中的值: (1)對(duì)數(shù)組C0,C3中的相應(yīng)元素進(jìn)行異或運(yùn)算,當(dāng)相應(yīng)元素出現(xiàn)空格值時(shí),運(yùn)算結(jié)果為空格值. 若非空格值元素的運(yùn)算結(jié)果都等于0,則輸出E(xi|xj);若非空格值元素的運(yùn)算結(jié)果都等于1,則輸出CE(xi|xj). (2)數(shù)組C1,C2中的相應(yīng)元素進(jìn)行異或運(yùn)算,當(dāng)相應(yīng)元素出現(xiàn)空格值時(shí),運(yùn)算結(jié)果為空格值. 若非空格值元素的運(yùn)算結(jié)果都等于0,則輸出N(xi|xj);若非空格值元素的運(yùn)算結(jié)果都等于1,則輸出CN(xi|xj). (3)數(shù)組C1,C3中的相應(yīng)元素進(jìn)行異或運(yùn)算,當(dāng)相應(yīng)元素出現(xiàn)空格值時(shí),運(yùn)算結(jié)果為空格值. 若非空格值元素的運(yùn)算結(jié)果都等于0,則輸出S(xi|xj);若非空格值元素的運(yùn)算結(jié)果都等于1,則輸出CS(xi|xj). (5)數(shù)組C2,C3中的相應(yīng)元素進(jìn)行異或運(yùn)算,當(dāng)相應(yīng)元素出現(xiàn)空格值時(shí),運(yùn)算結(jié)果為空格值. 若非空格值元素的運(yùn)算結(jié)果都等于0,則輸出S(xj|xi);若非空格值元素的運(yùn)算結(jié)果都等于1,則輸出CS(xj|xi). 步驟5 終止循環(huán). 程序流程圖如圖1所示. 圖1 程序流程圖Fig.1 The flow chart of the program 不同檢測(cè)方法之間的性能比較見(jiàn)表7. 圖形方法、譜系數(shù)方法、表格方法、快速算法都不適用于含無(wú)關(guān)項(xiàng)布爾函數(shù). 若被檢測(cè)布爾函數(shù)含無(wú)關(guān)項(xiàng),新算法明顯是最優(yōu)的; 若被檢測(cè)函數(shù)不包含無(wú)關(guān)項(xiàng),新算法在布爾函數(shù)的適用變量數(shù)、檢測(cè)類型、檢測(cè)過(guò)程復(fù)雜度方面也最有效. 表7 5種方法比較Table 7 Comparison of five methods 注n表示布爾函數(shù)變量數(shù). 提出了含任意項(xiàng)布爾函數(shù)的對(duì)稱變量檢測(cè)算法,該算法同樣適用于不含任意項(xiàng)的布爾函數(shù),為構(gòu)造密碼學(xué)函數(shù)和簡(jiǎn)化電路設(shè)計(jì)奠定了基礎(chǔ). [1] RICE J, MUZIO J. Antisymmetries in the realization of Boolean functions[C]//IEEE International Symposium on Circuits and Systems. Phoenix, AZ: IEEE,2002:69-72. [2] BLAIS E, WEINSTEIN A, YOSHIDA Y. Partially symmetric functions are efficiently isomorphism-testable[C]// IEEE 53rd Anual Smposium on Fundation of Computer Science.Washington: IEEE,2012:551-560. [3] PENG J, WU Q, KAN H. On symmetric Boolean functions with high algebraic immunity on even number of variables[J]. IEEE Transations on Information Theory,2011,57(10):7205-7220. [4] WANG H, PENG J. On 2k-variable symmetric Boolean functions with maximum algebraic immunity[J]. IEEE Transations on Information Theory,2012,58(8):5612-5624. [5] MUKHOPADHYAY A. Detection of total or partial symmetry of a switching function with the use of decomposition charts[J]. IEEE Transations on Electronic Computers,1963,EC(12):553-557. [6] HURST S L. Detection of symmetries in combinatorial functions by spectral means[J]. Electronic Circuits and System,1977,1(5):173-180. [7] KANNURAO S, FALKOWSKI B. Identification of complement single variable symmetry in Boolean functions through Walsh transform[C]// IEEE International Symposium on Circuits and Systems. Phoenix, AE: IEEE,2002:745-748. [8] 練益群,厲曉華,陳偕雄.基于表格法的部分對(duì)稱函數(shù)檢測(cè)[J].科技通報(bào),2005,21(2):214-217. LIAN Y Q, LI X H, CHEN X X. Detection of partial symmetric functions based on tabular method[J]. Bulletin of Science and Technology,2005,21(2):214-217. [9] 厲曉華,杭國(guó)強(qiáng),陳偕雄.邏輯函數(shù)對(duì)稱變量檢測(cè)算法[J].電路與系統(tǒng)學(xué)報(bào),2013,18(2):31-35. LI X H, HANG G Q, CHEN X X. The algorithm for identifying symmetric variable of logical function[J]. Journal of Circuits and Systems,2013,18(2):31-35. ZHANG Yongbo1, LI Xiaohua2 (1.CampusInformationCenter,TourismCollegeofZhejiang,Hangzhou311231,China;2.CampusInformationCenterofZhejiangUniversity,Hangzhou310027,China) To simplify the process for identifying 12 types of symmetric variables in Boolean function, we propose a new symmetry detection algorithm based on minterm expansion of Boolean function with don’t-care-terms. By analyzing the constraint conditions of the order eigenvalues matrixes for 12 types of symmetric variables, the algorithm for identifying symmetric variables of Boolean function with don’t-care-terms is proposed. The results show that, the new algorithm method is superior than the traditional methods in the applicability of the number of logical variables of Boolean function including don’t-care-terms, detection types, and complexity of the identification process. symmetric variable;the order eigenvalues matrix;Boolean function;truth table;don’t-care-terms 2016-05-19. 國(guó)家自然科學(xué)基金資助項(xiàng)目(61471314);浙江省公益技術(shù)研究社會(huì)發(fā)展項(xiàng)目(2014C33042). 張永波(1970-),ORCID:http://orcid.org/0000-0001-9529-3851,男,高級(jí)工程師,主要從事計(jì)算機(jī)應(yīng)用與網(wǎng)絡(luò)信息安全研究. *通信作者,ORCID:http://orcid.org/0000-0003-2482-9000,E-mail:xiaohua@zju.edu.cn. 10.3785/j.issn.1008-9497.2017.02.011 TN 431 A 1008-9497(2017)02-186-05 An algorithm for identifying symmetric variables of Boolean function with don’t-care-terms. Journal of Zhejiang University(Science Edition), 2017,44(2):186-190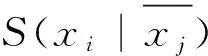
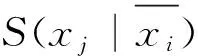

3 不同檢測(cè)方法的比較

4 結(jié) 論

 浙江大學(xué)學(xué)報(bào)(理學(xué)版)2017年2期
浙江大學(xué)學(xué)報(bào)(理學(xué)版)2017年2期
- 浙江大學(xué)學(xué)報(bào)(理學(xué)版)的其它文章
- 中國(guó)古文獻(xiàn)記載中“死者萬(wàn)計(jì)”事件的時(shí)空特征與原因分析
- 不同類型旅游移民的地方認(rèn)同建構(gòu)研究
——以麗江古城為例 - 父母教養(yǎng)方式與高中生自我監(jiān)控學(xué)習(xí)的關(guān)系
——核心自我評(píng)價(jià)的中介作用 - 中國(guó)特有植物諸葛菜屬(十字花科)的分類研究
- 基于區(qū)間數(shù)的直覺(jué)模糊多屬性決策研究
- A note of generalized shift-splitting preconditionersfor nonsymmetric saddle point problems
