第一學段學生幾何直觀能力的培養

李凡國

幾何直觀作為《義務教育數學課程標準（2011年版）》的核心概念之一，愈來愈成為數學教學關注的焦點。幾何直觀主要是指運用圖形描述和分析問題，借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果。幾何直觀是影響中小學數學發展的重要因素之一，培養和發展學生幾何直觀能力需要依托數學課程的每個領域，而不僅僅是“圖形與幾何”領域的任務[1]。可見，幾何直觀可以幫助學生直觀理解數學的本質，在數學學習中發揮著重要作用。宋建泳老師說：“幾何直觀能力的孕育階段主要是指一、二年級，過渡階段是三、四年級，萌發階段是四年級，生長階段是五、六年級。”[2]據此本人認為第一學段是發展學生幾何直觀能力的啟蒙階段，必須認真、細致地研究如何做好該學段學生幾何直觀能力培養的啟蒙工作。本文試結合自己的教學實踐就該問題做一些探討。

一、關注直觀演示，在直觀感知中啟迪幾何直觀意識

小學數學概念形成的一般過程是：觀察和觸摸客觀事物，形成表象，然后比較、分析、綜合形成概念。因此，觀察和觸摸是培養學生空間觀念的主要途徑。數學知識本身是抽象的，而第一學段學生年齡小，主要以形象思維為主，這是一對矛盾。要解決這對矛盾，必須重視直觀演示的作用，通過直觀演示經歷觀察觸摸實物—形成表象—形成概念，完成數學概念的形成過程。在這個過程中培養學生的觀察習慣、方法，使學生在直觀感知中發展空間想象能力，啟迪幾何直觀意識。如在一年級教學“10以內數的認識”時，通過擺小棒、畫圖形等直觀演示活動，使學生直觀形象地理解數的概念，讓學生在內心建立實物、圖形與數學概念的聯系。又如一年級教學“立體圖形的認識”時通過實物教具讓學生看一看、摸一摸，在教師的引導下發現不同立體圖形的特點，這樣的教學既輕松又便于學生記憶，讓學生在感知直觀優越性的同時培養空間觀念。再如二年級教學“角的認識”時利用圓規演示角的大小與邊的長短無關，只與兩邊的張開程度有關，學生在形象直觀中比較，進而培養其觀察能力。可見，實物直觀演示是數學學習的橋梁，在教學實踐中我們要讓學生養成借助實物理解數學概念、解決問題的習慣，同時由實物直觀向圖形直觀逐步過渡。

二、強化操作實踐，在直觀探究中培育幾何直觀能力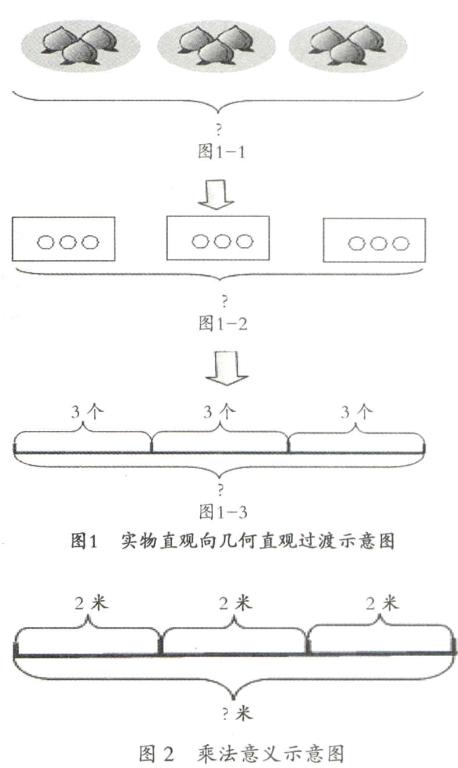

幾何直觀是數學活動經驗（實踐經驗和思維經驗）不斷積累所形成的數學素養，然而經驗的獲得需要親手觸摸、直觀感知、切身體驗，因此培養學生的幾何直觀能力必須加強學生的實踐操作活動，提高學生的動手能力。讓學生在看一看、做一做、拼一拼、搭一搭、折一折、剪一剪等實踐活動中親身體驗、直觀感知、積累經驗，進而實現由實踐經驗向思維經驗的過渡，在直觀探究中增強空間觀念，培育幾何直觀能力。如在二年級教學“平均分”時，教師提供學具讓學生動手分一分，提供圖形讓學生圈一圈，使學生在動手中牢牢把握平均分的意義和方法，讓學生在操作中感受幾何直觀的價值。又如二年級教學“有余數的除法”時，為了讓學生明白余數總是比除數小，給學生8根小棒讓學生擺正方形，關注剩下幾根，然后每次增加1根，同樣關注剩下幾根，教師引導學生將活動與除法算式聯系，從而探索發現余數總是比除數小的規律。這樣，將抽象的余數與形象的剩余小棒聯系起來，使學生感受幾何直觀可以把抽象的數學問題形象化。在教學中讓學生通過觀察、動手、動口、動腦等多感官活動，積累豐富的感性認識，形成嘗試利用感性認識去分析數學問題的能力。

三、加強圖形變換，在直觀體驗中發展幾何直觀能力

變換即讓圖形動起來，在變換中研究、揭示圖形的性質，有利于把握圖形與圖形之間的關系，有利于揭示圖形的本質特征，是發展幾何直觀的良好方法。因此，我們必須想盡一切辦法，讓圖形動起來，要么通過實物動態演示來實現，要么利用現代媒體動態模擬來實現，進而建立圖形運動表象，更好地揭示圖形的本質特征，在直觀體驗中發展幾何直觀能力。如二年級“旋轉的初步認識”教學中可以提供不同方向旋轉的兩個風車讓學生觀察，發現不同，然后用肢體語言描述不同的方向，接著教師介紹順時針旋轉和逆時針旋轉，讓學生用語言表述，最后請學生表演并描述旋轉。在這個過程中學生從直觀辨認到舉例描述，從生活語言的“轉動”到“繞著某某順時針或逆時針旋轉”的幾何語言的使用，有助于學生從空間感知走向空間表象的建立，形成幾何直觀能力。

四、重視數形結合，在直觀推理中拓展幾何直觀能力

數形結合是將抽象的數學語言與直觀的圖形結合起來，主要體現在兩方面：一方面是以形助數即利用圖形的直觀性來解決數量之間的關系問題，另一方面是以數解形即利用數量關系來揭示幾何圖形的性質。第一學段以理解、應用以形助數思想為主，因此提高學生以形助數的能力顯得尤為重要，培養學生以形助數的能力，必須從讀圖、畫圖兩方面進行培養。第一學段教材設計處處有圖片信息，在培養學生讀圖能力的同時，但還需要在讀圖的方法和技巧上下功夫，夯實學生讀圖的基礎。畫圖能力的培養，需要教師由實物直觀—實物圖—示意圖—線段圖逐漸抽象、逐步過渡，讓學生養成畫圖解決數學問題的習慣[3]。如二年級的一則例題：每個盤子里有4個桃子，3個盤子一共放了多少個桃子？可以通過實物圖呈現給學生（圖1-1），進而與學生討論畫桃子的實物圖太慢了，能不能用我們熟悉的數學圖形代替它，與學生達成共識后用○代替桃子畫出示意圖（圖1-2），教師提示如果用一條線段代替三個桃子這樣畫圖更加簡便快捷，引出線段圖（圖1-3）。這樣抽象培養學生的畫圖分析能力，由實物直觀向幾何直觀過渡，有助于學生幾何直觀能力的培養。又如在二年級教學“乘法的意義”時為了讓學生明白加法與乘法的關系，利用教學情境：袋鼠每次跳2米，3次跳多少米？引導學生畫圖（圖2），很快從圖中發現相同加數是2，總共跳了3次，即相同加數的個數是3，于是列出乘法算式：2×3。這一過程很好地將學生從抽象思維拖到形象思維，再到具體數字，學生很容易地理解了加法與乘法的關系。可見，數形結合可以利用圖形的直觀性幫助我們理解數學概念、明確算理、探索解決問題的思路。

綜上所述，在第一學段教學過程中培養學生幾何直觀能力，需要提供相應的素材，讓學生從實物直觀入手，建立實物直觀與數學知識的聯系，利用觀察實物和對實物的操作活動讓抽象的數學知識形象化、直觀化，形成利用實物直觀解決數學問題的能力，同時還需要從畫圖、讀圖入手，逐步培養學生運用圖形描述和分析問題的能力。讓學生養成用圖形說話的習慣，使學生的幾何直觀能力自然生長。

參考文獻

[1] 孔凡哲，史寧中.關于幾何直觀的含義與表現形式[J].課程·教材·教法，2012（32）.

[2] 宋建泳.小學生幾何直觀能力發展的幾個階段[J].小學數學教師，2015（3）.

[3] 蔡宏圣.幾何直觀：小學數學教學的視角[J].課程·教材·教法，2013（32）.

[責任編輯：陳國慶]