初中數學符號語言的教學策略

藍源添

【摘要】本文論述了初中數學符號語言的教學應結合初中生的思維特點，引導學生在理解數學符號的基礎上展開記憶，滲透符號化思想，促使學生在應用數學符號的過程中形成符號意識，養成規范、準確運用數學符號的良好習慣。

【關鍵詞】初中數學 數學符號 教學策略

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2017）02A-0078-02

眾所周知，數學符號是數學學科經過不斷傳承與發展而形成的專用語言，在世界范圍內通用。初中階段是學生使用數學符號的重要時期，但是，由于多方面的原因，當前初中生對數學符號的掌握和應用現狀存在著一些問題，主要表現為學生數學符號意識不強、符號記憶不夠清晰準確、書寫不夠規范、沒有養成使用數學符號的良好習慣等。為了讓學生更加高效地學習數學，準確地掌握數學符號語言，并可以靈活地應用，教師可以采用以下四種策略展開教學。

一、詮釋符號蘊含意義，幫助學生理解記憶符號

縱觀當前初中階段的數學符號語言學習活動，很多教師都是采取簡單直接的方式展開教學，讓學生機械地記憶數學符號。由于學生只能孤立地記憶數學符號的形狀，不能建立各種數學符號之間的聯系，所以大腦中存儲的符號信息也比較單薄。教師應結合不同的數學符號，挖掘符號所代表的意義，詮釋數學符號蘊涵的價值，幫助學生理解記憶，提升數學符號記憶的效果。

例如，在教學人教版數學七年級上冊《有理數的乘方》一課時，內容涉及an這個用來表示“乘方”運算的符號，以及由這個符號衍生出來的a2、b2、a3、b3等相關的數學符號。對于這些符號，學生只有清晰地理解符號代表的意思，才能準確地書寫，正確地解答數學題目。因此，筆者在教學時特別強調了對a2+b2、（a+b）2、a+b2、a3+b3、（a+b）3等一些常見的算式符號的意思，讓學生展開比較記憶，進一步培養學生思維的條理性。筆者先讓學生結合已經學習的知識，嘗試著逐一闡述各個算式的意思：a2+b2表示甲乙兩個數的平方和；（a+b）2表示甲乙兩個數和的平方；a+b2表示甲數與乙數平方的和；a3+b3表示甲乙兩個數的立方和；（a+b）3表示甲乙兩個數和的立方。最后讓學生進行對比，區別不同，加強學生對這些基本算式所表示的意思的理解，有效地幫助學生避免混淆這些數學符號，讓學生在今后的數學學習中正確使用。

理解記憶已經逐漸成為初中生記憶知識要點的主要方式。教師通過構建數學符號的意義體系，增強學生對數學符號相關信息的感知，讓學生在理解符號意義的基礎上進行識記，促使學生記得更加牢固。

二、講述歷史知識，引導學生學習內化符號

初中生的思維逐漸由形象思維向抽象思維轉變，對事物的認知也更加傾向于抽象的理性認識，對事物所形成的知覺也更加準確和快速，尤其是在觀察事物細節方面的能力有很大的提升，更擅長對事物細微差別的認識與把握。學生的這些認知能力的提升無疑對數學符號的學習是有幫助的。教師應結合初中生的能力結構和水平，通過講述一些數學符號的歷史，引導學生在記憶的基礎上快速內化并掌握數學符號。

例如，在教學八年級上冊《平方根》一課時，教材引入了“平方根號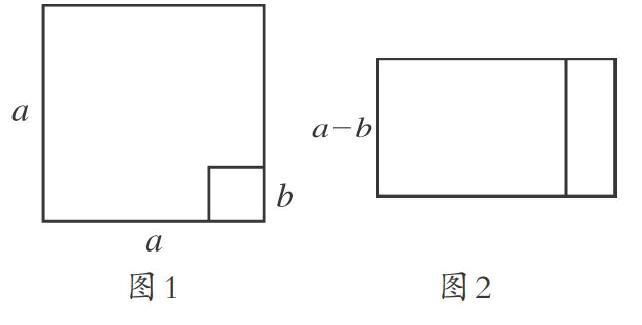”這一非常重要的數學符號，由于學生小學階段沒有接觸過有關根號的信息，無法產生聯想記憶，為了幫助學生準確地記憶和應用這一符號，教師對平方根號的由來進行了簡要說明：“在英語中，‘根的單詞是‘radix，而這個單詞追根溯源來自于拉丁文中的單詞‘Radix。開始人們用R和X兩個字母表示平方根號，但是比較復雜，在17世紀初期，數學家笛卡爾在編寫《幾何學》一書時，率先使用了‘√來表示‘二次根號。大家仔細觀察，笛卡爾當時用的這個符號與字母r比較像，也就是說二次根號的符號是由字母r變形得到的，后來因為需要表示‘開平方的范圍，所以在‘√的基礎上又增添了上面的‘-，從而變成了現在我們看到的‘的形式。”學生在聽完筆者的介紹后，對平方根號的發展演變獲得了一定的認識和了解，大腦中豐富了平方根號的信息，進而內化并吸收了這個符號。

三、創設解決問題情境，促使學生練習應用符號

應用數學符號解決實際問題既是學習掌握這種數學語言的最終目標，也是強化學生數學符號學習效果的有效途徑。教師應結合學生所學習的數學符號，運用恰當的方式為學生創設解決問題的情境，為學生提供應用數學符號的機會，讓學生可以自由地選用數學符號，準確地應用符號來解決問題。在這種真實的應用實踐中，通過有效地練習應用符號，達到掌握數學符號的最終目標。

例如，在教學八年級數學下冊《平行四邊形》一課后，為了增強學生數學符號的應用意識，筆者創設了一個解決問題的學習情境：“平行四邊形的底比高多10厘米，在這個平行四邊形上剪掉一個以平行四邊形的高為邊長的正方形，求剩余部分的面積是多少？”對這種問題，學生首先想到了平行四邊形的面積計算公式S=a×ht和正方形的面積計算公式S=a×a。接著，筆者讓學生根據題意“平行四邊形的底a比高h多了10厘米，即a-h=10cm”，那么，平行四邊行的面積減去邊長為h的正方形的面積，可以列出算式是S=a×h-h×h，然后把h=（a-10）代入，化簡后得到S=10a-100。學生在解答這個題目的過程中，自覺地運用了數學算式、數學符號，強化了對數學符號的記憶。在這樣的解題活動中，學生的數學符號意識得到了有效加強，學生應用數學符號解決實際問題的能力也得到了有效鍛煉。

學以致用可以強化學生對數學符號的認知，也能夠讓學生真正體驗掌握數學符號的意義和價值，從而產生強烈的學習數學符號的動機。教師通過為學生創造機會，加強數學符號的應用練習，提高了學生掌握數學符號的效果。

四、解析數學思想方法，增強學生認識理解符號

數學符號是數學語言的重要組成部分，而數學語言是數學思想方法的集中體現。教師通過為學生分析數學符號所包含的數學思想方法，以數學符號為載體和途徑，成功地向學生滲透數學思想，能夠促使學生數學思維的形成，指導自己的數學學習行為，也可以增強學生認識數學符號、拓展數學符號，讓學生能更加準確地應用數學符號。

例如，數學符號中有用字母來表示數字、用字母與幾何圖形一起來表示幾何圖形等，這些數學符號簡練地反映出了數字與數字、數字與算式等各種數學關系，體現了數學中最基本的“數形結合”的數學思想。筆者在引導學生學習數學符號的同時，也以數學符號為載體，對學生進行數形結合思想方法的滲透。“結合我們學過的數學知識，在圖形的幫助下，嘗試推導平方差公式，即a2-a2=（a+b）×（a-b）。”筆者設計學習任務，并且畫出了下面兩個圖形給學生提示。

學生根據筆者的提示，運用正方形、長方形的面積公式，結合圖形順利地推導出了a2-b2=（a+b）（a-b）。在這個過程中，學生不僅運用了數學符號、圖形符號，還親身體驗了數形結合的思想方法，從而加深了對數學符號的理解。

掌握數學符號，學好數學語言，不但是學好數學的必然要求，也是訓練學生數學思維、培養數學學習能力的重要手段。教師要積極探尋數學符號教學的有效手段，避免簡單機械的記憶，幫助學生正確地讀寫、規范地使用數學符號，開啟數學學習的大門，引領學生真正走進神奇的數學天地。

（責編 林 劍）