額外維個數及尺度對Casimir引力的影響

賴劼

（廣東技術師范學院天河學院，廣東廣州 510540）

1948年荷蘭物理學家亨德里克·卡西米爾提出了Casimir效應 （卡西米爾效應）[1],即兩塊靠得足夠近的金屬板將會產生相互吸引的現象，這個吸引力被稱作Casimir力：

它由普朗克常數?，光速c，和平板間的距離a的關系式來表示，它是作用于真空中的兩塊平行理想導體板單位面積相互的力,隨后的實驗驗證了該吸引力的存在。Casimir效應是一種有關真空漲落的量子現象，它起源于當量子化體積有邊界或者所在的空間為非歐幾里得時的真空擾動振幅的變化[2]。Casimir效應應用到物理學各個方面，包括弦論、基本粒子物理、M理論、宇宙學、拓撲缺陷、凝聚態物理的研究領域中都出現了有關Casimir效應的研究工作。

1 額外維對Casimir力的影響

為了探討額外維的個數及尺度對Casimir力的影響，我們分別就 3+1維、3+2維、3+3維情況下的Casimir力進行分析：

應用Casimir能量的定義：

由Casimir力等于能量的負導數，則Casimir壓強即為對能量求偏導數：

為了計算出Casimir壓強，根據第三類貝瑟爾函數的第一種變換式[3]：

我們得到存在1個額外維Casimir壓強：

存在2個額外維Casimir壓強：

存在3個額外維Casimir壓強：

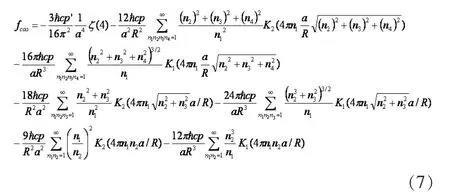
將不同額外維Casimir壓強的計算結果式 （5），式（6），式（7）進行數值比較。 得到式（5）、式（6）、式（7）在測量平行理想導體板的實驗誤差范圍在10%之內的考慮下，通過將存在額外維的平板計算的平板的力的結果進行優化處理，將得到了在實驗的誤差范圍內對額外維尺度大小的限制。平板間距離與額外維尺度大小的比值μ，通過這個比值大小的變化，我們可以清楚的得到額外維個數的增多，對額外維尺度大小的影響。在誤差范圍內，額外維個數對額外維尺度大小限制的變化。當兩個額外維的尺度不同時，在誤差范圍內，對額外維尺度大小限制的變化，結果表明當額外維的一個尺度在變小時，在實驗的誤差范圍內，平板間距和另一個額外維的尺度的比值在變小，即對這一個額外維尺度的限制范圍在變大。也就是說，要使額外維存在的條件滿足，與板間距相比的這一個額外維的尺度大小可以控制在一個更大的范圍內。并且，我們可以通過觀察發現，當兩個額外維的比值為0.2時，此時的板間距和其中一個額外維的比值等于只存在一個額外維，即5維時空的情況，也就是說，當兩個額外維的比值為0.2時，就與只存在一個額外維的情況沒區別了，而且，此后板間距同其中一個額外維的比值將不再發生變化，此時與板間距相比的那個額外維尺度的大小將對Casimir效應起到主導的作用。

我們將（5），式（6），式（7）數值計算結果制成表格1，以便對額外維尺度的增加，在誤差范圍內額外維尺度的限制的變化進行直觀的分析（其中= μ）。

表1 額外維尺度的限制的變化

通過表1，我們可以得出結論：我們發現板間距同額外維的尺度的比值確實因為額外維的個數的增加而變大，即對額外維的尺度的限制范圍變小。也就是說，要使額外維存在的條件滿足，額外維的尺度大小需要控制在一個更小的范圍內。這樣我們就可以證明出額外維個數的增加反而限制了額外維尺度的大小。

為了對不同額外維個數下Casimir壓強隨板間距離a變化有一個直觀的比較，我們將這三個結果進行繪圖分析，為了方便繪圖，我們令額外維的尺度大小都取 R，且 R=1，這樣式（5），式（6），式（7）計算的數值作出了以下的圖1。圖1表示出了沿與平板面垂直方向的Casimir壓強，分別在3維時空，3+1維時空，3+2維時空和3+3維時空尺度當R=1時的變化。

圖1 不同維度Casimir壓強變化趨勢

我們令式（6）中的 R1=R2=R，式(7)中的 R1=R2=R3=R，這樣式（5），式（6），式（7)的結果就會出現三項相同的項，而這三項剛好是式（5）的結果。為了清楚的得到額外維個數以及尺度大小的影響，我們需要從式（5），式（6）和式（7）中將這三項單獨分析，在跟式(6),式（7）剩余各項的結果分別進行數值比較，可得出以下結論：

為便于分析，我們令公式中，則相同的三項為：

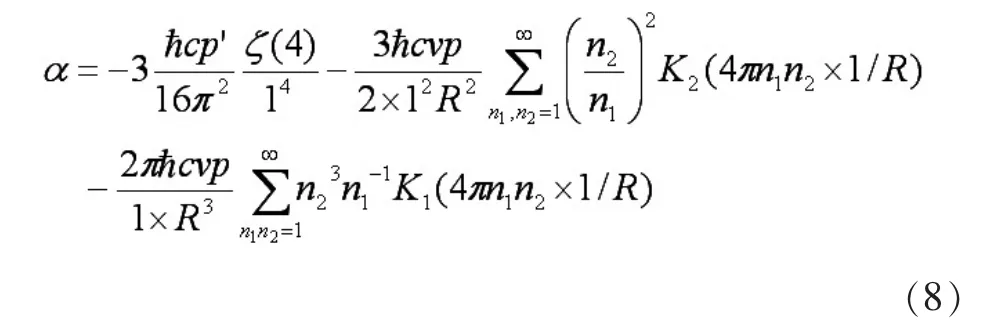
我們看到這里的α其實就是式（5）中的a=1的結果。

對于式（6），我們摘除上面的那三項后，同樣取a=1，剩余的各項為：

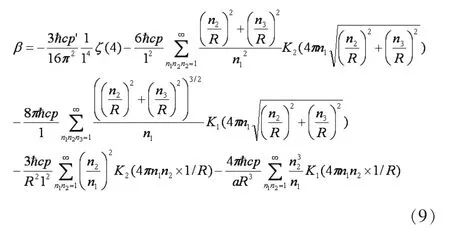
同理，對于式（7），我們摘除相同的三項后，取α=1，剩余的各項為：

對α，β，γ這三個參數式分別進行數值分析時我們取 ?=c=1，以及 p′=2，p=3。

表 2 是在分別取 R=1，2，3，4，5 的值時，α，β，γ 三式的具體對應數值。

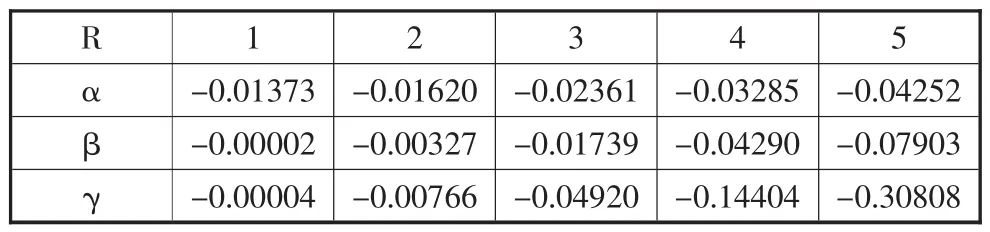
表2 α，β，γ變化數值

從表2中，我們可以得出結論：當額外維尺度時R=1，式（6），式（7）中起主導的項是跟式（5）中相同的那三項α，而當額外維尺度R≥2后式（6）和式（7）中除此三項以外的其余各項β，γ也開始發揮作用，我們看到而當 R=3時式（6）和式（7）剩余的項 β，γ的數量級已經跟式（5）中的那三項α的數量級相當了，當R≥4之后，剩余項β，γ的數值甚至超過了式（5）中那三項α的數值。

2 結語

通過表2的縱向比較也表明了隨著額外維個數的增加，Casimir吸引力是越來越來大的。并且額外維的尺度的大小對Casimir力也有影響，當額外維尺度R≥1時，額外維的個數幾乎對Casimir力的大小無影響，當R≥2時，額外維的個數才開始對力的大小發揮作用。

[1]Casimir HBG.On the attraction between two perfectly conducting plates[J].Proc K Ned Akad Wet，1948（51）:793-795.

[2]J.Strathdee.Kaluza-Klein Theory[J].Mod.Phys.A，1986（1）:1.

[3]王竹溪，郭敦仁.特殊函數概論[M].北京：北京大學出版社，2000.