緊扣“三個維度”有效拓展開放題的解題思路

◎張秀枝

緊扣“三個維度”有效拓展開放題的解題思路

◎張秀枝

隨著素質教育和創新教育的縱深推進，數學開放題的教育價值已被越來越多的數學教師認同。開放題沖破了傳統的限制，以它的開放性、靈活性、多變性給學生思維創設了更廣闊的空間，有助于激發學生的創新意識，養成創新習慣，發展思維的創造性，提高學生的分析問題、解決問題的能力。

怎樣提高學生解決數學開放題的能力呢？結合自己的實踐經驗，我認為拓展開放題的解題思路是解決開放題的金鑰匙。

一、借助假設法，拓展開放題的解題思路

假設法是數學中的重要解題方法之一，通過假設可以使復雜的問題簡單化，使所求的問題明朗化，幫助學生很快地找到解決問題的突破口，從而使問題化難為易。開放題的教學中，教師要引導學生大膽去假設。假設的目的不僅僅是為了解決問題，更重要的是讓學生的思維不局限于教師和課本講過的方法內容當中，開創發散思維和求異思維，從而培養其勇于探索，敢于創新的精神，使學生的創造能力更好地得以開發。例如：這道題答案無窮，可是剛一看這道題的時候，學生卻無從下手，于是我引導學生應用了假設法，先假設它們的結果都等于1，隨后，讓學生們嘗試解決問題。學生們通過自主學習與合作探究不僅得到了答案，而且，在這樣假設的引領下，不斷拓展解題思路。有的學生說也可以假設它們的結果都等于2，這樣得到的結果與假設結果等于1就不一樣了，有的說結果也可以等于……這樣應用假設法，很快就得到了答案。巧妙地運用假設法，不僅使稍微復雜的問題簡單化，而且，潛移默化中滲透著轉化的思想，讓學生在經歷學習的過程中落實“四基”，同時激發了學習數學的興趣。

二、張揚學生個性，拓展開放題的解題思路

弗來登認為，每個人都有自己的數學現實，即每個人都有自己的生活、工作和思考的特定客觀世界以及反映這個世界的各種數學觀點、運算方法和有關知識結構。開放題教學就為孩子們提供了一個這樣充分自由的環境。在一個班級里，孩子們的原有知識基礎、學習習慣、學習方法、理解與感受等能力各不相同。許多孩子喜歡按自己特定的方式發展自我。這種獨特的思維方式有時候是拓展開放題解題思路的金鑰匙。如：六年級學完“圓的面積”之后，整理復習中有一道求陰影部分面積的圖形題（見圖一）。大部分學生都想到用四分之一圓的面積減掉一個直角三角形的面積后再乘2。（見圖二）另一個學生則提出了這樣的做法：陰影部分的面積可以看做是一個半圓的面積減去一個大三角形的面積。（見圖三）我馬上表揚她不僅善于觀察而且善于思考。同時，鼓勵同學們繼續探究，看看還有什么好方法。一陣短暫地沉默后，學生們有了驚喜地發現。一位學生說：可以看做是一個大圓里畫一個最大的正方形，用大圓的面積減掉正方形的面積，再除以2（見圖四）；還有的想到，可以看做一個大的正方形里面畫一個最大的圓。先用正方形的面積減掉圓的面積，得到空白處的面積除以2，然后用圖上小正方形的面積減掉剛才求出的空白處面積……“問渠那得清如許，為有源頭活水來”，就是這獨特思維的源頭活水煥發了強大的生命力，讓我們看到了個性思維綻放的智慧火花。

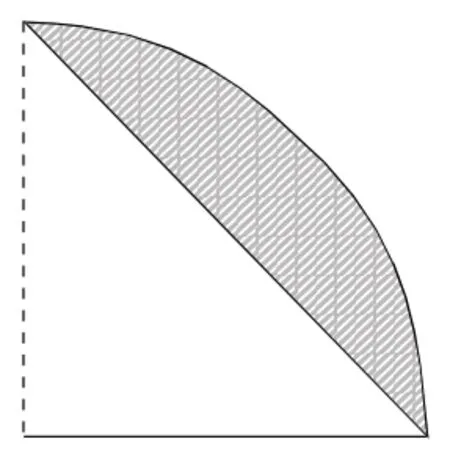
圖二

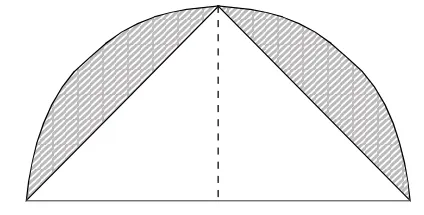
圖三

圖四

三、強化動手實踐，拓展開放題的解題思路

小學生心理發展的重要特點是，對新鮮的具體事物感興趣，善于記憶具體的事實，而不善于記憶抽象的內容。大教育家陶行知提出“知行合一”的教育理念，杜威也倡導“做中學”。可見，動手實踐活動正是數學知識的抽象性和學生思維的形象性之間架起的一座“橋梁”，是解決數學問題的有效途徑。如：一個正方形沿著一條直線切去一個角，還剩幾個角？這個問題剛出現時，孩子們會異口同聲地說：“還剩三個角”。這時候不急于告知孩子們答案，可以讓他們動手操作，拿出正方形剪一剪、在本上畫一畫。通過操作就會出現不同的答案。（如下圖）原來畫的方法不同得到的結果也不同。在小學數學教學過程中，教師要適當、充分地讓學生親自動手實踐，調動學生的積極性，使他們體驗到學習數學的快樂。同時在掌握知識的過程中，使學生的創新意識和創新潛能得到有效的發展。

四、有效利用封閉題的變式延伸，拓展開放題的解題思路

開放性問題教學一般安排在某一知識點、某一小節、某一單元、某一知識板塊的教學之后，教師可以對所學的新知識進行巧妙的延伸，適當滲透開放題的解題思路，開拓學生的視野，發展學生的思維。比如，在進行比、分數、百分數知識整理復習時有這樣一道題：甲數是乙數的，甲數比乙數少（），乙數比甲數多（）。很多學生一頭霧水，不知該從何下手，所做的答案更是五花八門。于是，在講解這道題時我并不急于告訴學生答案及做法，而是設計了這樣開放性的問題：見到甲數是乙數的，你想到了哪些數量關系？學生會在頭腦當中將學過的所有知識信息進行整合，展開豐富的聯想，得到了以下多種答案：1.甲數和乙數的比是2∶5；2.甲數是乙數的40%；3.甲數是甲、乙兩數和的；4.乙數比甲數多150%；5.甲數和乙數一共有7份，甲數占2份，乙數占5份……雖然學生存在著差異，但最少的也想出了2～3種答案。通過這種開放性問題的設計與教學，給學生創設了活學活用的機會，開闊了學生的思路，對解答之前的問題也得心應手了。學生的思維靈活性也得到了發展。

開放題的設計本身意在開發學生的解題思路，開發學生潛在的學習能力，開放性數學問題給不同層次的學生學好數學創設了機會，如果長此下去，拓展學生開放題的解題思路，會有力地發展學生的創新思維，培養學生的創新技能，提高學生的創新能力，也會讓學生的個性得到自由發展。

(作者單位：撫順市新賓滿族自治縣平頂山中心小學）

（責任編輯：楊強）