關于初中生銳角三角函數概念理解水平的調查分析

孫牟昕+景敏

[摘 要] 在數學課程標準和各版本教材中沒有將銳角三角函數分列到函數領域，但是銳角三角函數的名稱和數學本質都明確地體現出函數的味道。通過問卷的方式，對九年級學生對銳角三角函數概念的理解情況進行調查，并分析部分學生不理解銳角三角函數中的自變量和因變量以及對應關系，不能區分銳角三角函數與已學函數之間異同。

[關鍵詞] 銳角三角函數；調查研究

在日常教學中，初中數學教師普遍反映初中學生學習銳角三角函數比較困難，特別是對于三角函數概念的理解更顯得困難。同時初中數學教師也反映學生對銳角三角函數理解存在很多問題。為全面了解初中生學習銳角三角函數時的困難，以及困難產生的原因，我們進行了本次抽樣調查。同時也希望通過本次調查，能夠尋找和確定合理教學要求，適度調整教與學方式方法，從而使學生高水平地理解三角函數概念。

一、關于銳角三角函數的認識

在相似的直角三角形中，當銳角大小確定以后，直角三角形中某兩邊的比值就隨之確定，且有唯一比值與之對應。這就是說，針對每一個銳角，都有唯一一個數值與它對應。基于初中階段的函數定義：“設在一個變化過程中有兩個變量X與Y，如果對于X的每一個值，Y都有唯一的值與它對應，那么就說X是自變量，Y是X的函數”，銳角三角函數符合初中階段函數定義。但與一次函數、反比例函數和二次函數相比，銳角三角函數是一類特殊的函數。其特殊性主要體現在對應關系及其表示方式上。例如，一次函數對應關系中，函數值是通過對自變量的代數運算得到的，并且這種對應關系直接借助于該運算表達式進行表示。而銳角三角函數的函數值不是通過對自變量（角度）的代數運算表達式來表示，而是依托于直角三角形，通過確定與該角具有某種位置關系的某兩邊的比值得到的，并且使用比較抽象的符號表示某兩個邊的比值，且不同兩邊比值采用不同符號。

二、研究方法

（一）樣本

調查樣本選自三所學校，其中兩所學校是遼寧省課程改革示范校，共從中隨機選取九年級四個班的147名學生；另一所學校是鞍山市城鄉結合部某普通初中，從中隨機選取九年級一個班級的29名學生。由于這三所學校都采取了陽光分班，因此，這樣選擇調查樣本保障了樣本的代表性。

此外，調查的時間選擇在學生均已學習過一次函數、二次函數、反比例函數和銳角三角函數。

（二）調查工具

根據調查目的——調查學生對銳角三角函數概念的理解水平，將問卷分為以下三個方面：學生對函數基本概念的理解，對銳角三角函數概念的理解和銳角三角函數與其他函數的差異。為了考查學生對函數概念的理解情況，我們要求學生寫出函數的概念。為了考查學生對銳角三角函數本質的理解，問卷中設計了三個題目。一個是“你認為銳角三角函數的本質體現了什么”并給出三個選項，意在考查學生在有錯誤選項的干擾下能否選出銳角三角函數的本質描述。第二個題目是“只要角的大小確定了，那么這個角的三角函數值的大小也就確定了，請問你同意這種說法嗎？并寫出理由”，意在考查學生在特定情境下能否準確表述出銳角三角函數的本質。第三個題目是關于表達式中自變量與因變量的區分，目的為了考查學生在三角函數正弦表達式中能否準確運用函數的概念區分出自變量與因變量。此外，問卷中第四題讓學生敘述銳角三角函數與其他函數的不同，意在調查學生對已學知識的整理程度。在問卷題目的設計與修改過程中，我們對特級教師和數學教育研究者進行了訪談，尋求建議，經過反復修改最終確定了問卷的有效性。

三、調查結果

本次調查回收問卷176份，有效問卷161份，整理后得到以下數據。

（一）學生對函數概念的理解水平

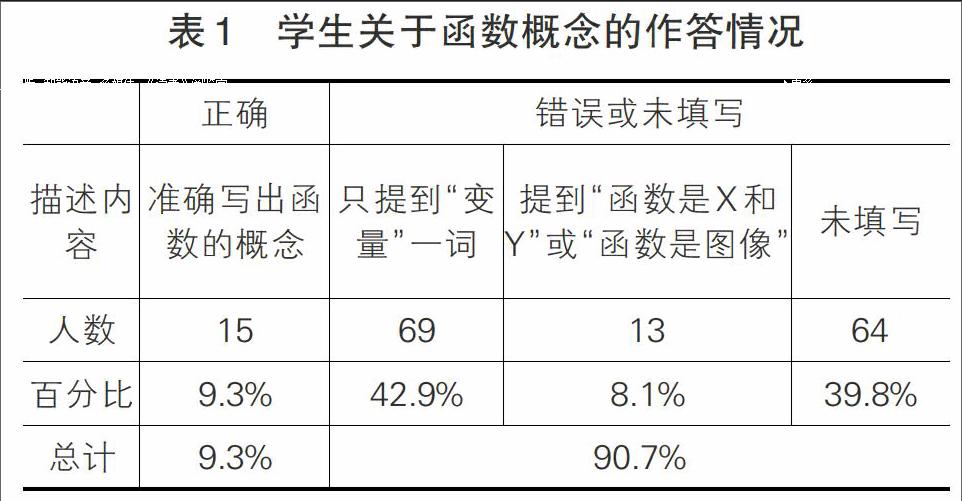
試卷中第三題是對學生函數概念理解水平的考查，要求學生寫出函數的概念，學生的答案基本分為四類，如表1所示：

9.3%的學生能正確書寫出函數的概念“設在一個變化過程中，有兩個變量X與Y，如果對于X的每一個值，Y都有唯一的值與它對應，那么就說X是自變量，Y是X的函數”。有42.9%名學生的答案中提到“變量”這一詞，例如，有學生寫到“函數就是兩個變量之間的關系”或“函數是變量X與變量Y的變化過程” 。但沒有進一步說明對應關系指的是什么，等等。可見，學生對函數概念理解的準確程度很低。還有一部分學生，雖然知道函數概念，但在表述上不準確不完整。

（二）學生對銳角三角函數本質的理解

試卷中第二題、第五題和第六題考查了學生對銳角三角函數本質的理解。第二題設計為“你認為銳角三角函數的本質體現了什么？”，并給出表2中的三個選項，其中C為正確答案。數據如表2所示：

從上題可以看出，學生正確選出銳角三角函數的概念的人數比較多。但仍舊有27.3%的學生不理解銳角三角函數的概念，分不清銳角三角函數中是哪兩個變量之間的對應關系。

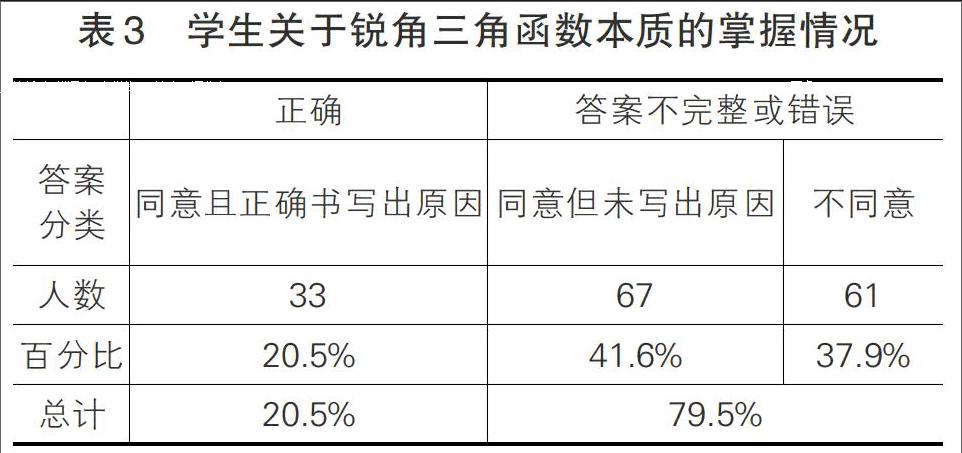
第五題是考查學生對銳角三角函數本質理解的判斷題，題目設計為“只要角的大小確定了，那么這個角的三角函數值的大小也就確定了，請問你同意這種說法嗎？并寫出理由”正確答案應是同意該說法。數據如表3所示：

從表3我們可以看出，學生對銳角三角函數本質的理解水平較低，只有20.5%的學生正確判斷并寫出自己的理由。例如，回答正確的學生提到“因為三角函數值是直角三角形中一個銳角的對邊和鄰邊的比，跟三角形的大小無關”或“大小不同的三角形是相似三角形，所以對應邊成比例，只要角一定，邊長比就一定”。無法表述原因或完全錯誤的學生占了大多數（79.5%）。

卷中第六題設計為關于表達式中自變量與因變量的區分，數據如表4所示：

本題為問答題，正確答案為∠A是自變量，是因變量。從問卷上可以看出還是有16.8%的學生能夠區分自變量與因變量的，說明這些學生理解銳角三角函數中函數變量的對應關系。而其余學生（83.2%）將邊長或∠A的正弦值當作變量的情況值得我們注意。

（三）關于學生對銳角三角函數與其他函數的區分

問卷中第四題考察了學生是否能準確區分銳角三角函數與其他函數的不同，請學生寫出關于銳角三角函數與其他函數的區別，數據如表5所示：

本題為問答題，請學生寫出銳角三角函數與一次函數、反比例函數和二次函數的區別。學生的答案可分為三類：“表達式不同”、“銳角三角函數是在固定的圖形中解決問題”、完全錯誤。數據顯示，學生在學習初中階段涉及到的各種類型函數后，對知識間的聯系程度較低，其表現是74.5%的學生說不出各個函數間的相同與不同之處。

四、討論

通過問卷調查，本次研究得到的結論是，學生對函數概念的理解水平較低，部分學生不理解銳角三角函數本質，大部分學生不能找出各個函數之間的不同之處。下面我們將從三個方面來分析學生產生問題的原因。

從銳角三角函數的表達式方面來看，由于給三種銳角三角函數賦予了特定的符號（sin、cos、tan）。這三個符號在一定程度上沒能夠直觀地給學生所謂的解析式的印象，隱去了函數與自變量之間的關系，即不能像一次函數那樣直接呈現函數與自變量的關系，使得學生理解銳角三角函數中的函數與自變量的關系變得困難。

從教材編排看，部分教材將《銳角三角函數》這節課放在一次函數、反比例函數甚至是二次函數之后出現，因此，一次函數、二次函數、反比例函數的學習對三角函數學習產生負遷移，即導致學生誤認為函數總是可以用X的解析式來表達的思維定式，從而影響了學生對銳角三角函數的理解。這種思維定式直接導致部分學生分不清銳角三角函數中的自變量和因變量，使得學生對銳角三角函數本質的理解出現困難。

從教師授課方面來看，教師沒有從函數概念的高度引導學生理解銳角三角函數，沒有說明銳角三角函數是明顯地存在“對應”關系的函數，更多的是關注特殊角度所對應的兩邊比值。這樣可能會導致一部分學生無法理解銳角三角函數的本質及與其他函數之間的不同之處。同時，大部分教師在講授函數部分知識的時候，重視習題練習要多于給學生傳授函數思想的應用，這樣會弱化學生在函數概念和函數思想上的認識。

[參 考 文 獻]

[1]石瑛.九年級學生對銳角三角函數的認知[D].華東師范大學，2009.

[2]濮安山.初中生函數概念發展研究[D].東北師范大學，2011.

（責任編輯：張華偉）