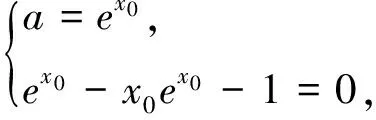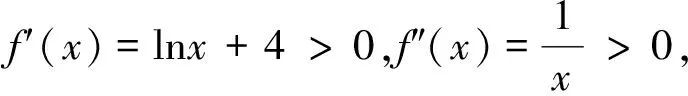利用“切線”處理函數(shù)中兩類不等式問題

江蘇省海門中學(xué) (226100) 吳燕梅

利用“切線”處理函數(shù)中兩類不等式問題

江蘇省海門中學(xué) (226100) 吳燕梅

在高三復(fù)習(xí)題中，涉及函數(shù)與導(dǎo)數(shù)的綜合問題常常會(huì)遇到不等式證明和不等式恒成立求參數(shù)范圍問題，解題常規(guī)方法集中在構(gòu)造函數(shù)求最值或分離參數(shù)求范圍.但有的疑難問題需要一些技巧，如：虛設(shè)零點(diǎn)估算最值，或者分離參數(shù)后需要借用高等數(shù)學(xué)洛必達(dá)法則來求最值，而本文以幾道例題說明：基于函數(shù)凹凸性下嘗試構(gòu)造“切線”來解兩類問題.

1.概念與性質(zhì)

1.1 函數(shù)的凹凸性定義

設(shè)f(x)為定義在區(qū)間I上的函數(shù)，若對(duì)于I上的任意實(shí)數(shù)x1,x2和實(shí)數(shù)λ∈(0,1)，總有f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)，則稱f(x)為下凸(凸)函數(shù).反之，如果總有f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2)，則稱f(x)為上凸(凹)函數(shù).

1.2 定理

設(shè)f(x)為區(qū)間I上的二階可導(dǎo)函數(shù)，則在I上f(x)為凸(凹)函數(shù)的充要條件是f″(x)≥0(f″(x)≤0)，x∈I.

1.3 性質(zhì)1

若函數(shù)f(x)是凸函數(shù)，則經(jīng)過其圖像上一點(diǎn)(x0,f(x0))的切線滿足不等式f(x)≥f′(x0)(x-x0)+f(x0)，當(dāng)且僅當(dāng)x=x0時(shí)不等式取等.

性質(zhì)2 若函數(shù)f(x)是凹函數(shù)，則經(jīng)過其圖像上一點(diǎn)(x0,f(x0))的切線滿足不等式f(x)≤f′(x0)(x-x0)+f(x0)，當(dāng)且僅當(dāng)x=x0時(shí)不等式取等.(證明略.)

2.策略與方法

2.1 凹凸性下構(gòu)造“切線”證明函數(shù)中不等關(guān)系

例1 已知f(x)=lnx,g(x)=ex，其中e是自然對(duì)數(shù)的底數(shù)，求證g(x)-f(x)>2.

證明：因?yàn)間′(x)=ex,g″(x)=ex>0，所以g(x)是凸函數(shù)，g(x)在x=0處切線為y=x+1，則由上述性質(zhì)1得ex≥x+1，當(dāng)且僅當(dāng)x=0時(shí)取等；同理可證f(x)是凹函數(shù)，在x=1處切線滿足不等關(guān)系lnx≤x-1，所以ex≥x+1>x-1≥lnx，又兩者取等條件不同，則ex-lnx>2，得證.

點(diǎn)評(píng)：上述方法是在兩個(gè)函數(shù)上各取一條切線構(gòu)造不等關(guān)系，利用兩條切線之間的位置關(guān)系(高低)轉(zhuǎn)化得證.

例2 已知函數(shù)f(x)=ex-ln(x+m).

(1)設(shè)x=0是f(x)的極值點(diǎn)，求m，并討論f(x)的單調(diào)性；

(2)當(dāng)m≤2時(shí)，證明f(x)>0.(2013年全國新課標(biāo)Ⅱ理21題)

解：(1)略.

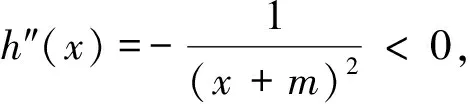
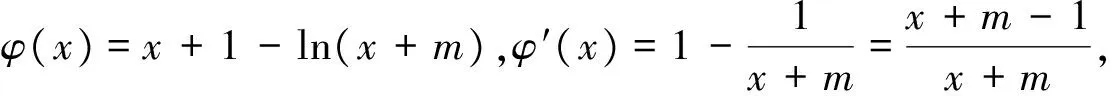
反思：若證形如不等式f(x)-g(x)>0，其中只有一個(gè)函數(shù)具有凹凸性，可嘗試上述方法：假如f(x)為凸函數(shù)，可先構(gòu)造切線證得f(x)≥f′(x0)(x-x0)+f(x0)，再證f′(x0)(x-x0)+f(x0)≥g(x)成立，檢驗(yàn)等號(hào)成立的條件.

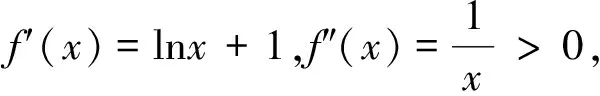
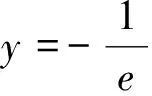
2.2 基于凹凸性巧用“切線”解不等式恒成立求參數(shù)范圍問題

例4 已知函數(shù)f(x)=x(ex-1)-ax2，當(dāng)x≥0時(shí)，f(x)≥0恒成立，求實(shí)數(shù)a的取值范圍.

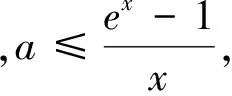
解法2：(直接研究函數(shù)最值)x≥0,f(x)≥0等價(jià)于x≥0時(shí)，ex-1-ax≥0恒成立.令h(x)=ex-1-ax，因?yàn)閔′(x)=ex-a，(ⅰ)若a≤0時(shí)，h′(x)>0，即h(x)在[0,+∞)上單調(diào)遞增，故h(x)≥h(0)=0成立；(ⅱ)若a>0時(shí)，令h′(x)=0，則x=lna.①當(dāng)lna≤0?00，故h(x)在[0,+∞)上單調(diào)遞增，h(x)≥h(0)=0成立；②當(dāng)lna>0?a>1時(shí)，x∈(0,lna)時(shí)，h′(x)<0，而x∈(lna,+∞)時(shí)，h′(x)>0，所以h(x)min=h(lna)，但h(lna)

點(diǎn)評(píng)：函數(shù)的凹凸性為構(gòu)造切線帶來可能，利用數(shù)形結(jié)合可以方便找到參數(shù)的臨界值進(jìn)而確定取值范圍，也能打破對(duì)常規(guī)方法的思維定勢(shì)，觸碰新的解題靈感.

例5 設(shè)k∈Z，當(dāng)x>1時(shí)，不等式k(x-1)

解法1：分離參數(shù)法(虛設(shè)零點(diǎn)求最值，估算k的范圍).

解法2：構(gòu)造函數(shù)h(x)=xlnx+3x-2-k(x-1)，討論確定函數(shù)的最小值h(x)min>0，求k的范圍.

由此可見，借用構(gòu)造“切線”為處理函數(shù)中不等式證明以及求解恒成立時(shí)參數(shù)范圍問題，提供了一種新的“視角”，當(dāng)然這樣的函數(shù)需要考察其“凹凸性”，利用數(shù)形結(jié)合的思想來分析問題.函數(shù)與導(dǎo)數(shù)的綜合問題一直是高考的熱點(diǎn)，而不等式的相關(guān)問題也是全國卷的常考題型，對(duì)于“她”的動(dòng)向研究是值得的也是有“意義”的事.