一道常見試題變式的再思考

江蘇省盱眙中學 (211700) 梁 義

一道常見試題變式的再思考

江蘇省盱眙中學 (211700) 梁 義

波利亞指出："掌握數學就是善于解題."在實現數學教學目的的過程中，教師應適時的引導學生從不同的方法、角度、思維方式去觀察、聯想、分析，根據問題的特定條件探索出一系列的解題思路，培養學生的發散思維能力.所以一題多解的教學顯得格外重要，它充分讓學生自己思維，讓學生整理，讓學生在探索中發現數學解題的本質，達到觸類旁通的效果.

下面筆者通過對一道高中常見試題的變式研究，來加以說明，希望對讀者有所幫助.

在教學中給出這題時，學生很自然地給出下面這種做法：

反思：本題中的輔助角雖然不是特殊角，但前面的系數“4,3”都是較為特殊的數，因此對輔助角的取值是可以確定的，所以借助以上方法可以解決.但對于更一般的角，如55°，我們在確定端點值時就顯得有點不知所措，這就需要我們結合各種知識，探究更多的解法，以便對這類題達到熟練解決.

方法二:(轉化為齊次式)

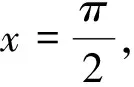
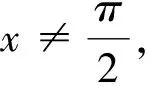
ⅰ)當t=0時，y2=16；

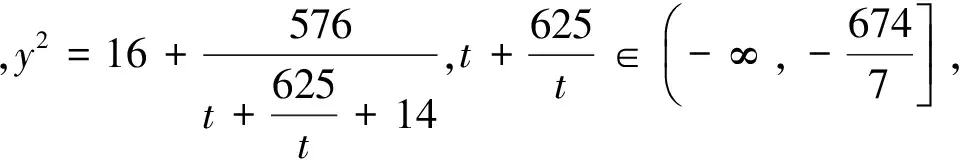
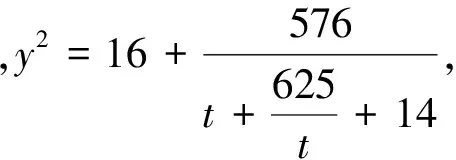
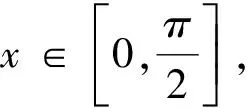
點評：上述方法借助構造齊次式，將問題轉化為分式型函數的值域問題，體現了轉化的思想，達到了簡化的效果！

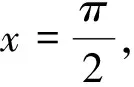
點評：作為求函數值域的強有力的工具，準確地求導，細致地劃分單調區間，是解決本題的關鍵所在.

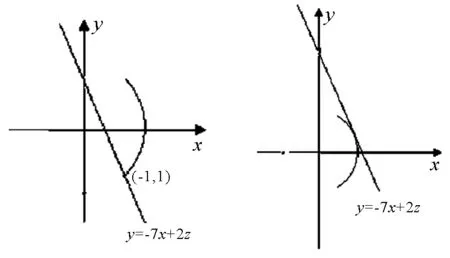
圖1

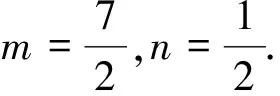
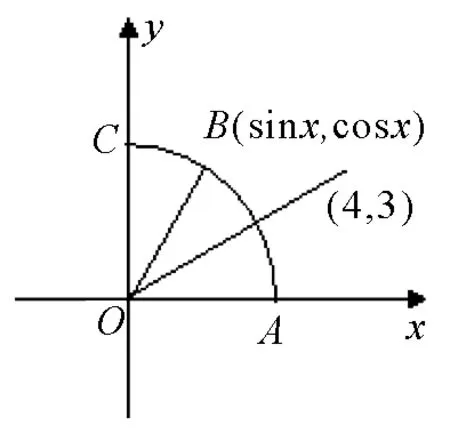
圖2

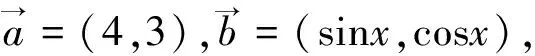
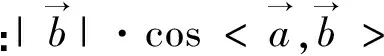
方法六:(點到直線的距離)

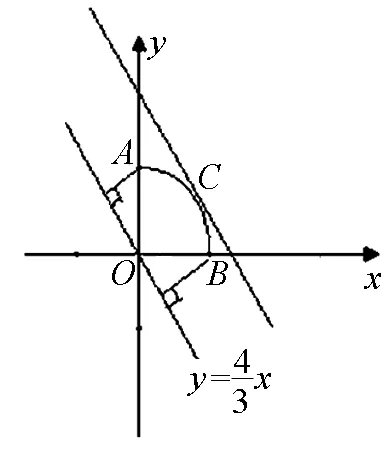
圖3

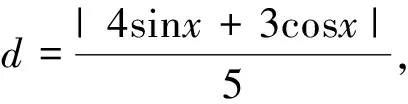
點評：數學家華羅庚曾說過：“數缺形時少直觀，形缺數時難入微”，這充分說明了數形結合思想的妙處，正確地建立數與形之間的聯系，構建模型，將給我們解題帶來更加直觀的感受.