再議ax=logax(a∈(0,1))的解

江西省臨川一中 (344100) 陸繼承 張珍珍

再議ax=logax(a∈(0,1))的解

江西省臨川一中 (344100) 陸繼承 張珍珍

對于ax=logax(a∈(0,1))的解的討論，似乎一直都沒有停止過，究其原因，主要是ax=logax(a∈(0,1))中的兩個簡單初等函數圖像畫在同一個坐標系里，直觀判斷很容易產生誤解，很多沒有深入討論的師生以為只有一個解，其實不然.不過到目前為止，對于ax=logax(a∈(0,1))的解的個數的討論結果已經沒有什么爭議了，但對于這個問題的證明，許多同行給出了獨到的見解，這里筆者效仿各位同行前輩，給出了自己的兩種證明過程，請各位同行們批評指正.

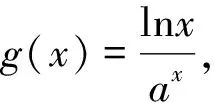
我們先分析函數y=xlnx，有y′=lnx+1，則

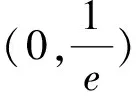
①當a∈[e-e,1)時，-e≤lna<0，所以有

圖1

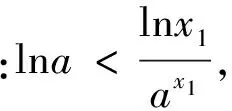
x1lna>lnx1+2ln(-lnx1)，

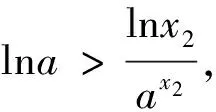
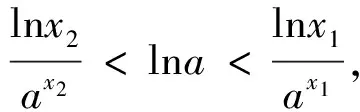
綜上：當a∈(0,e-e)時，ax=logax有3個解；

當a∈[e-e,1)時，ax=logax有1個解.

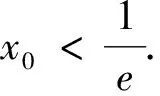
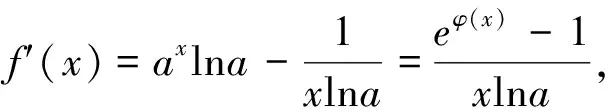
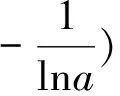
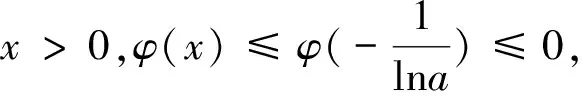
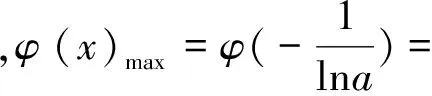
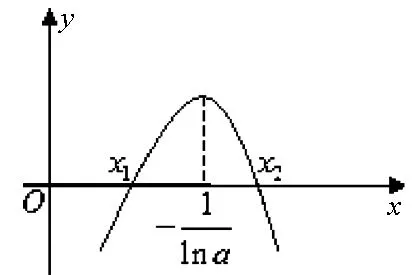
圖2

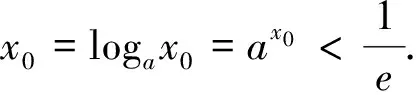
圖3

再令t=lnx0∈(-∞,

綜上：當a∈(0,e-e)時，f(x)=ax-logax=0有3個解；

當a∈[e-e,1)時，f(x)=ax-logax=0有1個解.