圓錐曲線切線的一條性質再探

北京市陳經綸中學 (100020) 張留杰 孫丕訓

圓錐曲線切線的一條性質再探

北京市陳經綸中學 (100020) 張留杰 孫丕訓

文[1]中結合一道試題探究了過橢圓(雙曲線)外一點所引的兩條切線的一條性質，并且僅僅局限于焦點在x軸的情況下，我們發現對于焦點在y軸時，相應結論也是正確的，所以可以將文[1]的結論改進如下：

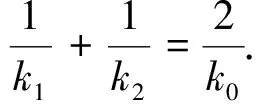
我們發現此優美結論與點M密不可分，即它在曲線W的一條對稱軸(y軸)上，如果直線AB與x軸相交于點N，那么k1、k2和直線PN的斜率k′會有何種關系呢？

經過探究，我們得出

結論2 過中心在原點、焦點在坐標軸上的有心圓錐曲線W外一點P引兩切線PA、PB，切點弦AB所在直線與x軸交于點N，當直線PA、PB、PN的斜率存在且不為零時，設它們的斜率分別為k1、k2、k′，則k1+k2=2k′．

下面以橢圓為例進行證明，如圖1．

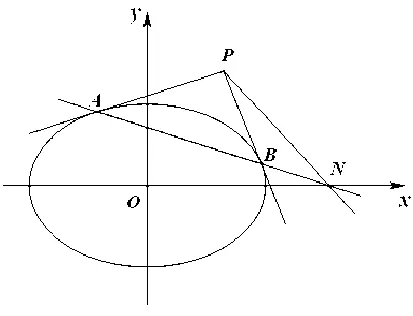
圖1

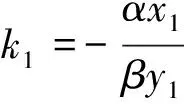
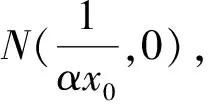
同理，在雙曲線中，也不難證明該結論成立．

由結論1和結論2，我們不難得出關于橢圓和雙曲線切線的一個性質定理：

能否將此定理的結論推廣到拋物線呢？

由于拋物線可以看作是“另一頂點在無窮遠點”的橢圓，所以拋物線的另一條對稱軸也可以認為在無窮遠處，于是過拋物線外一點引兩條切線PA、PB，切點弦AB所在直線與另一條對稱軸的交點M(或N)就在無窮遠點，所以PM(或PN)應該與AB平行，其斜率k0(或k′)等于直線AB的斜率k．于是我們得出如下定理：

定理2 過頂點在原點的拋物線W外一點P引兩條切線PA、PB，切點分別為A、B，直線AB與拋物線的對稱軸交于點M，設切線PA、PB的斜率分別為k1、k2，直線AB的斜率為k，直線PM的斜率為k0，當k1、k2、k、k0均不為零時．

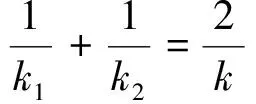
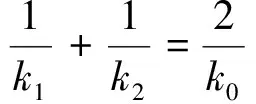
下面以對稱軸為x軸的拋物線為例進行證明．

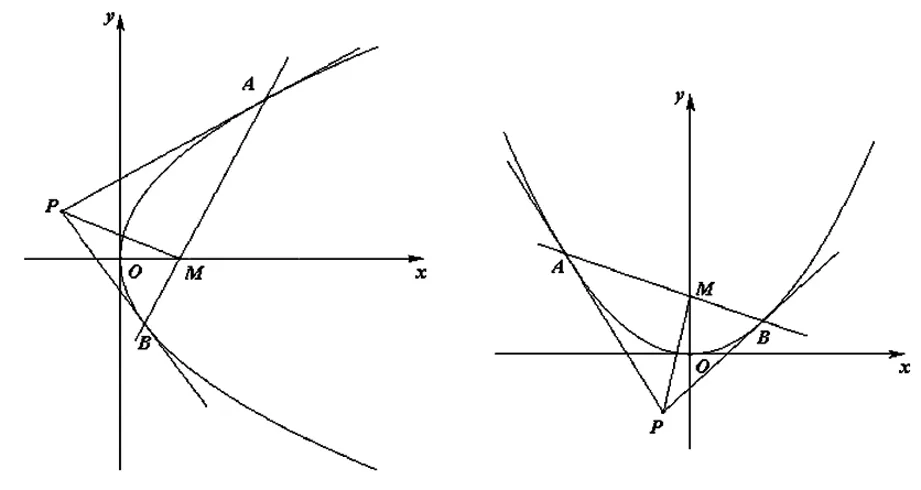
圖2 圖3

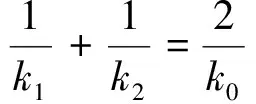
[1]劉宜兵，廖 華.一道高三調研試題的結論推廣[J].中學數學研究(江西)，2016,7.