厚度 寬度 深度：數(shù)學活動經(jīng)驗需要審視的三重維度

呂程+++李洵

【摘 要】當下對數(shù)學基本活動經(jīng)驗的研究，陷入了教育理論和實踐探索的兩難。要破解這一難題，首先應該正確把握數(shù)學活動經(jīng)驗的內在本質。在此基礎上，從以下三個方面在教學中加以落實：1.在反復經(jīng)歷的過程中，增加學生數(shù)學活動經(jīng)驗的厚度；2.關注不同能力的學習者的活動體驗，拓展數(shù)學活動經(jīng)驗的寬度；3.充分經(jīng)歷推理的過程，加深數(shù)學活動經(jīng)驗的深度。

【關鍵詞】數(shù)學活動經(jīng)驗 三重維度 厚度 寬度 深度

在數(shù)學教育史上，傳統(tǒng)的“雙基”教學影響了我國幾代人的成長，然而《義務教育數(shù)學課程標準（2011年版）》（以下簡稱《課標》）中在原有“雙基”的基礎上，拓展為了“四基”，即“基礎知識、基本技能、基本思想、基本活動經(jīng)驗”。其中《課標》中，明確提出了相應的課程理念，即“教師教學應該以學生認知發(fā)展水平和已有的經(jīng)驗為基礎，面向全體學生，注重啟發(fā)式和因材施教……使學生理解和掌握基本的數(shù)學知識與技能，體會和運用數(shù)學思想與方法，獲得基本的數(shù)學活動經(jīng)驗”。[1]可見，基本活動經(jīng)驗的提出，是新課標中重要的變化之一，同時學生活動經(jīng)驗的積累也是當前一線教學中重要的教學目標之一，正因為此，關于數(shù)學活動經(jīng)驗的研究至今仍是熱點問題。

“數(shù)學活動經(jīng)驗”在《課標》中提出，已有四年，那么一線的數(shù)學教師是不是真正提升了有關數(shù)學活動經(jīng)驗的認識，從而更好地指導教學實踐了呢？基于一線教師的問題，數(shù)學活動經(jīng)驗又該如何去真正認識，從而更有利于學生能夠更好地獲得數(shù)學活動經(jīng)驗呢？筆者將在教育理論和實踐的層面，試圖從數(shù)學活動經(jīng)驗的三重維度，來進一步探討教師如何正確認識數(shù)學活動經(jīng)驗，以及如何促進學習者獲得數(shù)學活動經(jīng)驗的有效策略。

一、困惑：數(shù)學活動經(jīng)驗的理論與實踐探索的兩難

（一）教師有數(shù)學活動經(jīng)驗的培養(yǎng)意識，但實踐困難

從當前一線教學的層面來看，有研究者對當前小學數(shù)學教師數(shù)學活動經(jīng)驗的教學情況做過調查研究。[2]從收集的數(shù)據(jù)來看，有97.9%的教師認為教學中需要重視數(shù)學活動經(jīng)驗的發(fā)展程度，有79.5%的教師了解數(shù)學活動經(jīng)驗的作用。可見數(shù)學活動經(jīng)驗對于學生數(shù)學學習的重要程度，已被一線教師認可，并且對數(shù)學活動經(jīng)驗有所認知。可另外一組數(shù)據(jù)就不那么樂觀了，有62.7%的數(shù)學教師認為在實際的日常教學中去培養(yǎng)小學生的數(shù)學活動經(jīng)驗比較困難，甚至無從下手。從以上一組數(shù)據(jù)來看，在實踐層面，數(shù)學活動經(jīng)驗的相關研究成果并未轉化為教師指導實踐的有利手段。

（二）數(shù)學活動經(jīng)驗的研究成果眾多，但未及本質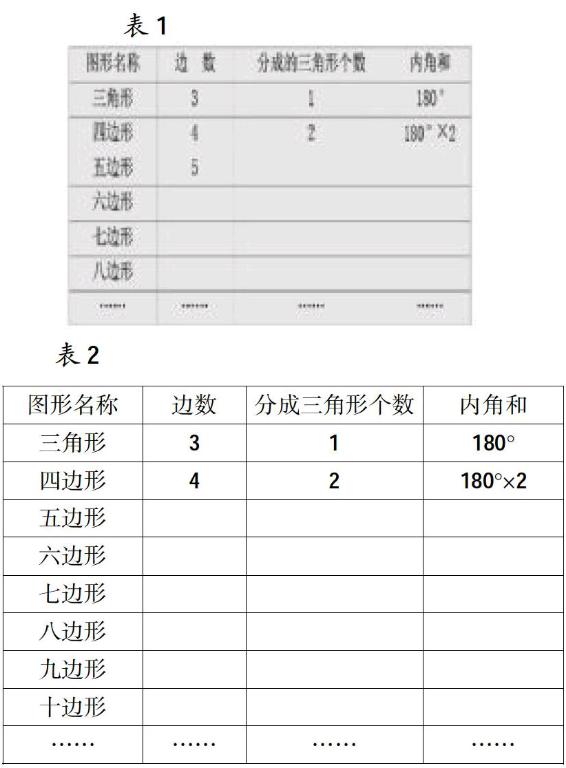

從中國知網(wǎng)的文獻搜索結果來看，有關數(shù)學活動經(jīng)驗的研究多達443篇。從文獻的數(shù)量角度，也反映了數(shù)學活動經(jīng)驗受到了眾多教學研究人員、一線教師的廣泛關注。對于數(shù)學活動經(jīng)驗的相關教學，涌現(xiàn)了不少頗有價值的想法。如：吳正憲認為教師需要幫助學生在數(shù)學活動探索、解決問題的過程中不斷積累數(shù)學活動經(jīng)驗；[3]賁友林認為數(shù)學活動經(jīng)驗不僅可以在學生的親自體驗中獲得，同時可以在替代性經(jīng)驗中獲得；[4]郭青松以“圖形與幾何”領域為例，讓學生在“經(jīng)歷”到“經(jīng)驗”的過程中獲得數(shù)學活動經(jīng)驗；[5]宋煜陽以等積變形問題為例，談到過程性則是數(shù)學活動經(jīng)驗積累的根本原則。[6]類似的研究，或結合課例，或以某個數(shù)學領域為例，或以某個數(shù)學問題，給一線教師提供了一些操作性的建議。但從這些文獻來看，都出現(xiàn)了一個值得商榷的問題，即都避談了什么是數(shù)學活動經(jīng)驗而去研究怎樣積累數(shù)學活動經(jīng)驗。簡言之，拋開了數(shù)學活動經(jīng)驗的本質，去思考教學實踐問題，從一定層面上來說，讓數(shù)學活動經(jīng)驗的研究走向了一個誤區(qū)。

二、思源：數(shù)學活動經(jīng)驗本質的再認

筆者的研究團隊在對多地教研人員和一線教師的訪談中發(fā)現(xiàn)，當前數(shù)學活動經(jīng)驗研究的兩難問題，究其原因在于數(shù)學活動經(jīng)驗的本質未被一線教育者所明確。又因為對于數(shù)學活動經(jīng)驗的不同理解，從而衍生出了不同的對數(shù)學活動經(jīng)驗積累的操作性建議，以至于出現(xiàn)了對數(shù)學活動經(jīng)驗教學盲從的當下局面。

回歸《課標》，筆者發(fā)現(xiàn)第四部分實施建議中，提及了“數(shù)學活動經(jīng)驗的積累是提高學生數(shù)學素養(yǎng)的重要標志”“幫助學生積累數(shù)學活動經(jīng)驗是數(shù)學教學的重要目標，是不斷經(jīng)歷、體驗各種數(shù)學活動過程的結果”。看來《課標》未明確涉及數(shù)學活動經(jīng)驗的本質。再通過對《課標》解讀來看，提到了對數(shù)學活動形式的闡述，如觀察、試驗、猜測、驗證、推理與交流等，要求學生能將相關的經(jīng)驗遷移運用到后續(xù)的數(shù)學學習中去[7]。由此可見對《課標》的解讀也未進一步明確數(shù)學活動經(jīng)驗本質是什么，如何去正確認識。但是筆者在《課標》（實驗稿）中找到了有關數(shù)學活動經(jīng)驗本質的線索。在《課標》（實驗稿）中提到數(shù)學知識包括數(shù)學事實和數(shù)學活動經(jīng)驗。可見，數(shù)學活動經(jīng)驗是一類知識。筆者的研究團隊，經(jīng)過多年來的教學實踐和與多位資深數(shù)學教育專家的交流，得出結論：數(shù)學活動經(jīng)驗的本質是一種具有過程性、個體性、實踐性的隱性知識。同時根據(jù)數(shù)學活動的存在形式的劃分，數(shù)學活動經(jīng)驗可以分為數(shù)學操作活動經(jīng)驗（以下簡稱操作經(jīng)驗）和數(shù)學思維活動經(jīng)驗（以下簡稱思維經(jīng)驗）。在之前的研究中，筆者提出了思維經(jīng)驗應當在教學實踐中被作為數(shù)學活動經(jīng)驗的內在精髓，[8]隨后史寧中先生也以思維經(jīng)驗為研究對象，對初中學生數(shù)學基本活動經(jīng)驗進行了進一步的量化研究。[9]至今有關思維經(jīng)驗的研究仍被作為研究數(shù)學活動經(jīng)驗的熱點問題。

三、突圍：基于數(shù)學活動經(jīng)驗本質的教學建議

通過上述的研究，筆者將在數(shù)學活動經(jīng)驗的本質特征的前提下，從理論和實踐的角度，去進一步探討如何幫助學生積累數(shù)學活動經(jīng)驗。

（一）在反復經(jīng)歷的過程中，增加學生數(shù)學活動經(jīng)驗的厚度

[案例一]三年級數(shù)學活動課“對折問題”

師：老師這里有一張和黑板上一樣的紙條，你會對折嗎？誰來幫老師對折一下？咱們先想象一下，對折打開，會把這張長方形紙條怎么樣呢？

生（小結）：對折就是把長方形紙條平均分成了2份。

師：那同樣的紙條，我們把剛才對折后的紙條，再對折，也就是對折了幾次？（兩次），長方形紙條平均分成了幾份呢？估一估。到底是不是這樣，看來還得動手折，驗證一下。

生（小結）：對折再對折，就是把紙條平均分成了4份。

師：那么接下去，你們知道老師會提什么問題嗎？

生：對折3次，平均分成了幾份。（師折，學生先不折）

師（追問）：先想一想，對折3次平均分成了幾份呢？誰來猜一猜？

師：看來意見不統(tǒng)一，怎么辦？

生自己折一折，驗證。

生猜后，匯報交流。

小結：對折3次其實就是把長方形平均分成8份。

師：回過頭來看，把紙條平均分成2份，我們是怎么折的？平均分成4份，怎么折的呢？8份又是怎么折的？（隨機板書）

師小結：看來對折和我們學過的什么知識有關啊？（板書：平均分）

師：對折1次，平均分成了2份；對折2次，平均分成4份；對折3次平均分成8份……觀察一下，對折兩次的前后份數(shù)變化，有沒有什么規(guī)律啊？

生（總結）：對折前的份數(shù)，是對折后份數(shù)的一半。

這是在學習完三年級“平均分”之后的一堂校本數(shù)學活動課，本堂課讓學生在經(jīng)歷折紙的過程中，去感悟折紙的次數(shù)與平均分的關系，體現(xiàn)了生活與數(shù)學的聯(lián)系。在多次反復的折紙過程中，同時伴隨著對問題的反思，學生積累的不僅僅是“折”這一數(shù)學操作活動經(jīng)驗，而更多的是“折”的背后所蘊含的折的次數(shù)與平均分份數(shù)之間的關系。可見反復的伴隨思維的數(shù)學活動，可以在習得數(shù)學知識的同時，內化數(shù)學操作活動經(jīng)驗。

（二）關注不同能力的學習者的活動體驗，拓展數(shù)學活動經(jīng)驗的寬度

關于數(shù)學活動經(jīng)驗，陳佑清也認為數(shù)學活動經(jīng)驗屬于個體知識的范疇，[10]那么數(shù)學活動經(jīng)驗就存在著個體性的特征。換句話說，不同（能力）的學習者在經(jīng)歷某個數(shù)學學習活動的過程中，所獲得的數(shù)學活動經(jīng)驗的程度是不同的。

[案例2]蘇教版四年級綜合實踐課“探究多邊形的內角和”

本課從特殊的四邊形內角和開始，學生經(jīng)歷了從一般四邊行內角和的驗證到五邊形內角和的探索，再到其他多邊形內角和的拓展。其中有一個細節(jié)，當學生自主探索到四邊形內角和（180°×2）之后，教師放手讓學生自主探索其他多邊形的內角和公式，蘇教版教材提供了一個表格（見表1）。

而有的學優(yōu)生可以通過對四邊形的內角和的探索，能夠通過類比、歸納，運用數(shù)學直覺得出其他邊形的內角和公式，從而得出結論，而有的學困生在對八邊形的探索之后依舊無法發(fā)現(xiàn)規(guī)律。因此，教學中可以將表格適度調整為表2。

經(jīng)過這樣調整，給予學生更多的操作空間。學生可以基于之前積累的數(shù)學操作經(jīng)驗，自主發(fā)現(xiàn)更多的多邊形內角和公式，從而便于得出一般多邊形的內角和的公式；而這樣的調整，可以關照到部分學困生，讓其有更多的空間去操作，感悟多邊形內角和的數(shù)學模型。所以在教學中關注不同學習者在數(shù)學活動中的體驗，拓展數(shù)學活動的寬度，也是以人為本、尊重學習者個別差異性這一理念的重要體現(xiàn)。

（三）充分經(jīng)歷推理的過程，挖掘數(shù)學活動經(jīng)驗的深度

數(shù)學活動經(jīng)驗具備隱性知識的特征，就需要學習者思維的參與，尤其是需要讓學生在推理的過程中，培養(yǎng)學生的創(chuàng)新能力，這是數(shù)學基本活動經(jīng)驗提出的初衷。[11]以“分數(shù)的基本性質”一課為例，在通常的教學中，執(zhí)教者設計看圖寫分數(shù)并找出一些分子分母不同但大小相等的分數(shù)，接著通過一些數(shù)學活動，尋找和相等的分數(shù)并用等式表示，進而讓學生在發(fā)現(xiàn)結論的基礎上揭示分數(shù)的基本性質。

【環(huán)節(jié)2】在經(jīng)過學生自由驗證一個分數(shù)的分子和分母同時乘相同的數(shù)，分數(shù)的大小不變的時候，教師進一步引導學生從已有的結論中通過適當變換、聯(lián)想，同樣可以形成新的猜想進而得到新的結論。比如分數(shù)的分子和分母還可以同時……進而自主地引發(fā)學生對“一個分數(shù)的分子和分母同時除以相同的數(shù)，分數(shù)的大小不變”這一規(guī)律的猜想和驗證。

通過環(huán)節(jié)1，我們發(fā)現(xiàn)，在探索一個分數(shù)的分子和分母同時乘相同的數(shù)，分數(shù)的大小不變的時候，第一次經(jīng)歷了“猜想—驗證”的過程，從而發(fā)現(xiàn)規(guī)律；而環(huán)節(jié)2，則是基于第一次數(shù)學思維活動的經(jīng)驗，再一次探索分數(shù)的分子和分母同時除以相同的數(shù)，分數(shù)的大小不變。從這兩個細節(jié)中學生發(fā)現(xiàn)規(guī)律并不是教師有意識的引導達成的，而是學生的主動建構，同時是伴隨著數(shù)學活動經(jīng)驗的積累，而且在驗證過程中，學生經(jīng)歷了歸納推理的過程，從而實現(xiàn)了數(shù)學知識的再創(chuàng)造。數(shù)學活動經(jīng)驗作為一種隱性知識，也正是在學生不斷深入的思維過程中得以顯性化，進而獲得數(shù)學活動經(jīng)驗。

參考文獻：

[1]義務教育數(shù)學課程標準（2011年版）[M].北京：北京師范大學出版社，2012：3.

[2]李高慧.小學生數(shù)學活動經(jīng)驗的教學現(xiàn)狀調查研究[D].西南大學.2014.

[3]吳正憲.感悟數(shù)學思想，積累數(shù)學活動經(jīng)驗[J].小學教學（數(shù)學版），2012，（1）：13-15.

[4]賁友林.關于數(shù)學活動經(jīng)驗的三點認識[J].小學教學（數(shù)學版），2012，（7-8）：109-110.

[5]郭青松.從“經(jīng)歷”走向“經(jīng)驗”[J].教育研究與評論（小學教育教學）.2012，（6）.

[6]宋煜陽.過程性：數(shù)學活動經(jīng)驗積累的應然之道[J].教學與管理，2012，（6）.

[7]義務教育數(shù)學課程標準（2011年版）解讀[M].北京：北京師范大學出版社，2012.

[8]呂程，蔡慶有.思維經(jīng)驗：數(shù)學活動經(jīng)驗的內在精髓[J].教學與管理，2013.10.

[9]郭玉峰，史寧中. 初中學生數(shù)學基本活動經(jīng)驗的量化研究[J].課程·教材·教法，2013，（11）：48-54.

[10]陳佑清.教學論新編[M].北京：人民教育出版社，2011：125.

[11]郭玉峰，史寧中.數(shù)學基本活動經(jīng)驗：提出、理解與實踐[J].中國教育學刊，2012，（4）：42-45.

（江蘇省南京市建鄴實驗小學 210019江蘇省南京市教育科學研究所 210002）