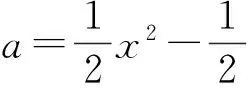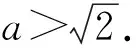數形結合思想方法

●張春杰 (學軍中學 浙江杭州 310012)

數形結合思想方法

●張春杰 (學軍中學 浙江杭州 310012)

數形結合思想是數和形的完美統一，也是最能體現數學美感的數學思想.數形結合思想在高考中屬于重點考查范疇.文章通過分析典型范例，引導學生如何從數中尋找形，也就是挖掘題目最本質的背景，再對形進行定量的分析，體現數學嚴謹入微的分析思想.

數形結合;形由數生;數來析形

1 知識內容

數形結合思想是高中階段非常重要的思想方法.正如華羅庚先生所說：數缺形時少直觀，形缺數時難入微，數形結合把基本知識和基本圖形有效地結合起來，能有效考查學生的核心數學素養.數形結合思想一般包含2個維度：

1)形由數生.圖形的構造不是憑空的，是在分析題意的基礎上生成的,使問題直觀化.

2)數來析形.數學是嚴謹的，在從圖形中尋找到問題的突破口之后，需要嚴謹的代數分析，使問題嚴謹化.

2 命題分析

近3年的浙江省數學高考試卷呈現2個重要特點：首先是強調了幾何背景下的代數敘述，解決問題需要回到最原始的幾何背景中尋找思路，這是最能凸顯本質的解決方法；其次是重點考查數形結合思想的掌握程度.比如，2016年浙江省數學高考理科卷的第3，6，7，14，15，19題和2016年浙江省數學高考文科卷的第3，4，8，13～15，19題都是和數形結合思想密切相關的高考題.從《2017年浙江考試說明》來分析，數形結合思想仍是考查的重點和熱點.

圖1

3 典題剖析

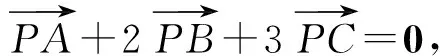
S△PAD=S△PAE=S△PDE.

不妨將此面積記為6,則

S△PAB=3,S△PAC=2,S△PBC=1,

即

S△ABC=S△PAB+S△PAC+S△PBC=6,

故

S△ABC∶S△PAC=6∶ 2=3.

評注 本題的關鍵在于形的遷移和轉變，從△ABC遷移到△ADE，從而讓點P從一個不熟悉的位置遷移為△ADE的重心.“從不熟悉到熟悉，從一般到特殊”是本題的點睛之筆，為本題的順利解決邁出了關鍵一步.接下來就是簡單的代數運算.

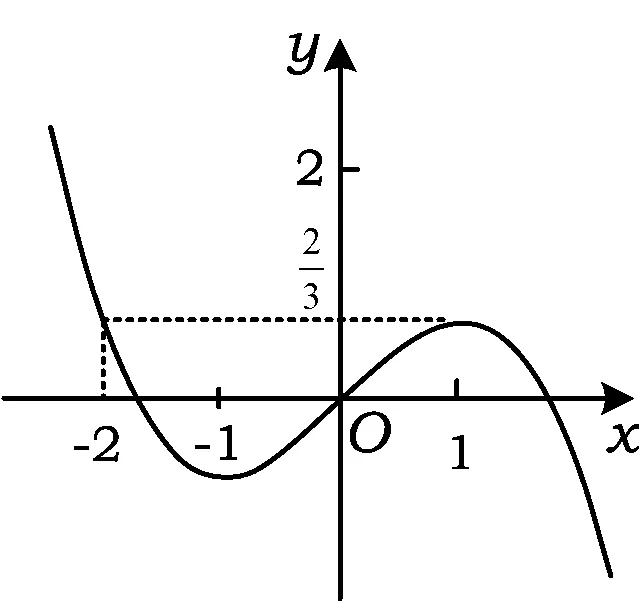
圖2

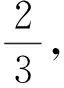
評注 求解本題的關鍵在于圖形的分析，尤其是注意到開區間的因素,不過，從圖2很容易得出取得最大值的條件.

例3 若向量a,b滿足|b|=3，|a|=2|b-a|，求|a|的取值范圍.

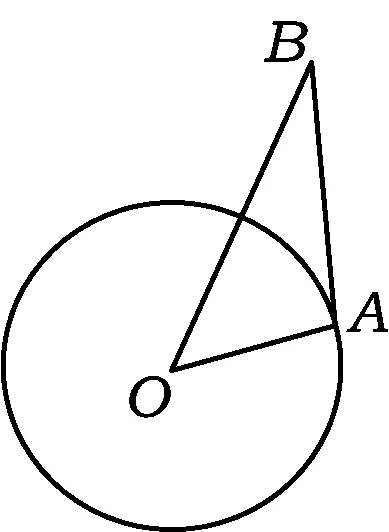
圖3

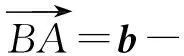
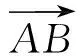
評注 幾何背景下的向量問題是浙江省數學高考命題的特色之一.本題體現了這一命題思路，沒有繁雜的語言敘述，寥寥幾筆就把幾何背景的代數形式交代清楚了.

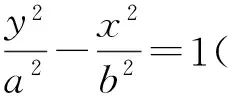
圖4 圖5

評注 解析幾何中的存在性問題一直是高考的熱點和難點.本題就是抓住問題的本質，轉化為學生比較熟悉的直線與圓的關系問題.

例5 已知函數f(x)=2x2ex與g(x)=3xex+a的圖像有且只有2個公共點，求實數a的取值范圍.

解 由2x2ex=3xex+a，可知

a=h(x)=2x2ex-3xex=x(2x-3)ex,

從而

h′(x)=(2x2+x-3)ex.

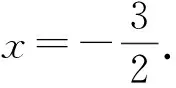
評注 把函數的交點問題轉化為方程問題，再從方程問題轉化為函數問題，利用函數的圖像，很容易找到解決問題的方法.

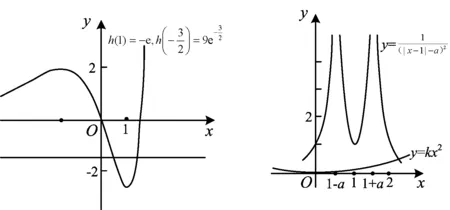
圖6 圖7

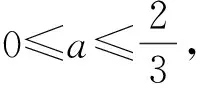
評注 恒成立問題也是各種層次考試重點考查的內容.本題的突破口在于形的構建和數的分析，緊緊抓住這一突破口，再分類討論，水到渠成.

4 精題集萃

1.已知互相垂直的平面α,β相交于直線l,若直線m,n滿足m∥α,n⊥β,則

( )

A．m∥lB.m∥nC.n⊥lD.m⊥n

( )

( )

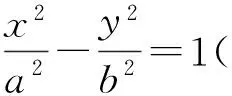
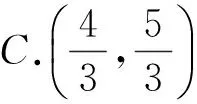
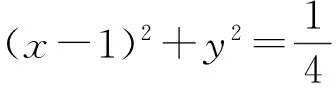
8.設關于x的方程x2-ax-1=0和x2-x-2a=0的實數根分別為x1,x2和x3,x4，若x1

9.已知函數f(x)=mx|x-1|-|x|+1,試討論函數f(x)的零點個數.

參 考 答 案

8.解 由x2-ax-1=0可知

由x2-x-2a=0可知

9.解 首先x=1為其中一個零點.令f(x)=0,則

10.解 假設有4個交點，不妨設橢圓的左側有2個交點P，Q，其中直線AP的斜率為k1,直線AQ的斜率為k2,則

化簡可知

故

2016-12-22；

2017-01-10基金項目：浙江省杭州市教育科研立項課題(14G1410)作者簡介：張春杰(1974-)，男，河南潢川人，中學高級教師.研究方向：競賽數學和創新人才培養模式.

O123.1

A

1003-6407(2017)02-23-03