解析延拓課程教學改革淺探*
——兼談最大熵方法

呂建平

(安徽師范大學物理系 安徽 蕪湖 241000)

解析延拓課程教學改革淺探*
——兼談最大熵方法

呂建平

(安徽師范大學物理系 安徽 蕪湖 241000)

針對數學物理方法課程教學中學生普遍反映比較抽象的解析延拓部分，設計以數值模擬方法為技術路線的教學方案.通過物理模型的構建，介紹線性響應理論和最大熵解析延拓方法的基本原理，全面設計課堂教學環節，展示對具體實例的計算結果.最后，對課程實踐過程中的有待提高之處進行反思和探討.

數學物理方法 解析延拓 最大熵方法

數學物理方法課程是高等院校物理類本科專業必修的重要課程之一.然而，對中等程度的學生而言，學好這門課程并不容易.學生在學習過程中既需要高等數學等前期數學課程的良好基礎，又需要對一些經典物理模型有清晰的認識[1,2].由于上述客觀原因，加之筆者水平所限，在承擔安徽師范大學卓越理科實驗班數學物理方法課程之初，筆者常在課堂教學設計過程中感到困惑.通過課堂教學的反饋，常獲悉學生在學習過程中感到概念過于抽象，無法和具體的物理系統進行有效聯系.

和國內多數高校一樣，我校數學物理方法課程在低年級開課，此時學生對一些重要物理問題的圖像和機理還沒有全面的認識.這要求教師在教學過程中，在有限的教學時長內補充介紹相關物理模型.而幾乎所有經典教材在講述偏微分方程部分時都會引入包括電導、熱傳導在內的輸運過程作為主要物理模型.這引發筆者的思考：既然學生在數學物理方法課的學習過程中須對輸運過程的物理圖像有基本概念，可否將輸運過程的相關模型拓展到偏微分方程以外的教學內容？此為筆者探索相關課程設計的背景.

本文討論解析延拓的教學設計，旨在借助于較為具體的物理圖像來避免教學內容過于抽象化，以探索提升教學質量的途徑.沿用吳崇試先生《數學物理方法》教材中關于解析延拓的概念[2]: 兩個函數f1(z)和f2(z) 分別在定義域g1和g2內解析，且在g1和g2的公共區域等價，則f2(z)可稱為f1(z)在g2區域的解析延拓，且f1(z)可稱為f2(z)在g1區域的解析延拓.又由同一性原理可知，對定義在同一個區域的兩個解析函數，如果它們在該區域內的無窮多個點上相等，且這些點中有聚點存在，這兩個函數必然在整個區域上等價.在多體物理系統的研究中常須借助于多種關聯函數.在頻域復平面上，延遲關聯函數和相應的松原關聯函數在無窮多個點上相等，且這些點中存在聚點(此處聚點為虛軸上正方向的無窮遠點i∞)，因而必然在共同解析區域上等價，且松原關聯函數可延拓到延遲關聯函數的解析區域.在實際計算中，由于一些數值算法在計算松原關聯函數時具有顯著的優勢.因此，在通常情況下，我們總是先直接計算松原關聯函數，再借助于解析延拓手段探索延遲關聯函數.

基于上述論證，同時借助于數值模擬方法，筆者將針對輸運問題設計解析延拓教學方案，進而在實際教學中進行小范圍實踐.下文將對教學過程的設計原理和基本環節進行介紹，并對教學實踐進行反思和總結.

1 物理問題的提出

輸運過程有廣泛的范疇，在物理學的教學和研究中具有重要的地位.輸運過程研究的常用理論框架之一為線性響應理論.線性響應理論對近平衡態系統的輸運行為有良好的描述.根據線性響應理論，我們只需要知道以時間為變量的電流-電流延遲關聯函數，就可根據久保公式方便地計算出電導率[3].然而，如何求得電流-電流關聯函數？首先，借助于數值模擬可獲得電流-電流松原關聯函數[4].接下來，可根據解析延拓手段由松原關聯函數獲得相應區域的延遲關聯函數.關于電流-電流松原關聯函數的計算，筆者通過前期科研工作已有方法上的積累，既可將程序代碼以軟件的形式提供給學生使用[5～7]，也可為學生直接提供松原關聯函數的數據.無論哪種做法，都不會直接影響學生在解析延拓方面的訓練.

在對物理系統平衡態性質的討論中，基于松原虛時的路徑積分蒙特卡洛方法已被廣泛采用.然而，本教學過程涉及輸運過程的數值實驗，對蒙特卡洛方法有更高要求.原因是顯然的：此處蒙特卡洛數據只是解析延拓的輸入數據，而不再是與實驗可比的最終結果.一旦蒙特卡洛數據的精度不高，或抽樣數據之間的關聯性不能被明確把握，相關的解析延拓過程就難以獲得穩定可靠的結果.因此，高效的蒙特卡洛算法是必要的技術手段.在課程教學中，我們將使用高效的蠕蟲型連續虛時蒙特卡洛算法，該算法通過新自由度的引入使得位形空間得以擴展，進而以馬爾科夫鏈的形式產生可供抽樣統計的位形.這種新位形的產生方式具有克服臨界慢化的功能，因而算法效率將獲顯著提高.在此過程中，學生須知道松原關聯函數的形式特點：若考慮頻域復平面，在虛軸的松原頻率點上松原關聯函數可以直接計算，且等同于相應的延遲關聯函數.

如前文所述，在物理上更重要的是實時延遲電流-電流關聯函數.若已知松原關聯函數在上半平面內一些點上的數值結果，如何通過解析延拓，獲得無限靠近實軸時的關聯函數數據？不失一般性，在已獲得松原關聯函數數據的情況下，可通過最大熵解析延拓辦法獲得以實頻為變量的延遲關聯函數，進而求得電導率.

2 最大熵解析延拓方法

通過多體物理理論中常用的萊曼(Lehmann)譜分解可知，在遠離實軸的上半頻域復平面內，延遲關聯函數在形式上等價于相應的松原關聯函數.在松原頻率上，后者可由量子蒙特卡洛模擬直接測量.為探索實軸上的信息，可作解析延拓iωn→ω+i0+，其中ωn為松原頻率.我們擬采用的最大熵方法是最具代表性的解析延拓方法之一[8,9].最大熵方法的主要思路是運用貝葉斯推理，把尋找最可能解析延拓結果的問題，轉化為求解“自由能”最小值的問題，它的穩定性已被大量文獻結果所證實.值得一提的是，最大熵方法對具有數值不確定性的數據具有強大的處理能力.在實際應用中，我們借助于高效量子蒙特卡洛方法產生的松原關聯函數具有高度的精確性，完全可以通過最大熵方法獲得穩定可靠的實頻輸出數據.另外，我們擬定的課堂教學方案中也包含了可靠的誤差估計方法.他山之石，可以攻玉.在未來的教學過程中，我們也有可能借鑒其他的解析延拓方法，如隨機優化方法[10]和隨機抽樣方法[11]，將它們作為傳統最大熵方法的重要補充.

最大熵方法最早發展于工程科學領域，后被物理學家借鑒，用來解決具有數值不確定性數據的解析延拓問題[8].首先，根據相關問題情境，引入“自由能”的概念.“自由能”的定義為F=χ2-AS，在形式上與熱力學中的自由能類似，其中χ2是描述擬合過程的協方差，S是相對于預設默認模型的熵密度，A是常系數，它的選取有不同的判定方法.而S類似于熱力學中的熵，此即為最大熵方法名稱的由來.我們不難想象，當A=0時，F中協方差χ2占主導地位，解析延拓過程就完全退化為數據擬合過程，擬合結果通常為噪聲結果，不具有預測能力；當A很大時，S占主導作用，擬合結果對應于平庸的默認模式.這兩種極限下，解析延拓結果都沒有意義.實際上，根據χ2隨熵權重變化的依賴關系可區分3個截然不同的區域：噪聲擬合區域、信息擬合區域和默認模型區域.對這3個區域的探討和分析，將有助于我們正確使用并最終發展最大熵方法[9].

在通過編程實現解析延拓的過程中，我們會盡可能地納入有效信息而完全避免噪聲信息.為此，我們把噪聲擬合區域和信息擬合區域的分界點作為熵權重的最佳選擇，并通過分析不同類型的熵權重選擇方法，探索最佳的解析延拓方案.從理論上講，無論輸入數據是否有數值上的不確定性，最大熵方法都應該給出唯一穩定的解析延拓結果.但值得注意的是，熵權重的選取會影響誤差估計的可靠性.而目前較為流行的熵權重選取方法是基于經驗判據，即令協方差χ2等于樣本數.該判據僅在樣本數很大且χ2精確可知的情況下較好地工作，因而不是我們的選擇.

3 課堂教學的實例

根據輸運過程的基本特征，借助于相關的理論和方法，并考慮課堂教學的實際情況，我們擬定了如圖1所示的課堂教學基本流程.

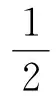
其中T為溫度，kB為玻爾茲曼常數.若僅關注平衡態行為，通過附加的模擬可確定此時系統處于正常流體態，其低溫下的超流特性被熱漲落破壞，但仍然保留普通流體的一些特征，包括擴散性和可壓縮性.我們在前文中提到的蒙特卡洛方法對該系統具有較為強大的刻畫能力.

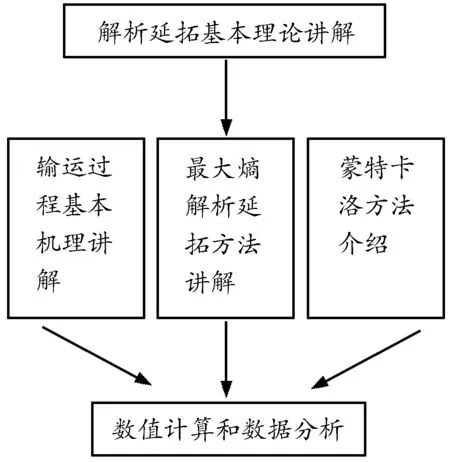
圖1 課程教學的基本流程

通過數值模擬，我們獲得了系統在平衡態的一系列數據.在圖2中，我們展示了以虛頻為自變量的電流-電流松原關聯函數.不難發現，該函數以較快的速度衰減.又由線性響應理論可知，以實頻為變量的電流-電流延遲關聯函數的虛部與電導率的規則項對應.為獲得該延遲關聯函數的虛部，我們采用上文中提到的、經過優化的最大熵方法進行解析延拓.如圖3所示，我們獲得了電導率隨實頻率變化的關系.和我們的預期一致，相關的解析延拓手段展現出高度的精確性和穩定性，這一點體現為解析延拓結果極窄的上下界范圍.最后，我們將直流(ω=0)電導率的規則項確定為0.085(2).

圖2 高溫下正常流體態的松原流-流關聯強度(已設=1，

圖3 高溫下正常流體態的電導率，所取參數與圖2相同

4 總結和反思

通過將數值模擬方法引入到解析延拓課程相關章節的教學過程中，學生可獲得對解析延拓理論及其實踐方法的直觀印象.通過與實際物理問題的結合，學生意識到相關教學內容在現代物理研究中的重要性，因而在一定程度上增強了學習的積極性.然而，筆者也清楚地認識到教學過程中的若干不足之處.例如，產生松原關聯函數的過程對學生而言類似于一個“黑匣子”，學生很難全面地理解數值模擬的細節，這可能會在一定程度上削減學生參與相關數值實驗的熱情.在數學物理方法課程的教學中，如何在有限的教學時長內，讓學生通過課本知識獲得完整解決一個實際物理問題的體驗？以本文為起點，在后續的教學實踐過程中，筆者將繼續修正相關的課程教學環節，以期獲得教學效率的持續提高.

1 四川大學數學學院高等數學、微分方程教研室．高等數學(第4冊)(第3版).北京: 高等教育出版社, 2010.76～98

2 吳崇試.數學物理方法.北京：北京大學出版社, 1999.137～144

3 列夫·達維多維奇·朗道,E·M·栗弗席茲.理論物理學教程:統計物理學(第5版)．束仁貴,束莼，譯.北京:高等教育出版社,2011.337～347

4K.Binder(edit.).TheMonteCarloMethodinConden-sedMatterPhysics.Germany:Springer, 2012

5J.P.Lv,Q.H.Chen,Y.Deng.Two-specieshardc-orebosonsonthetriangularlattice:AquantumMonteCarlostudy.Phys.Rev.A, 2014,89:013628

6J.P.Lv,G.Chen,Y.Deng.Z.Y.Meng,CoulombliquidphasesofbosonicclusterMottinsulatorsonapyrochlorelattice.Phys.Rev.Lett.115,2015:037202.

7J.P.Lv.Kaleidoscopeofsupersolidphasesofinterac-tinghard-corebosonsonthedicelattice.TheEuropeanPhysicalJournalB,2015,88:13

8M.Jarrell,J.E.Gubernatis.Bayesianinferenceandtheanalyticcontinuationofimaginary-timequantumMonteCarlodata.PhysicsReports1996, 269:133

9D.Bergeron,A.M.S.Tremblay.Algorithmsforopti-mizedmaximumentropyanddiagnostictoolsforanalyticcontinuation.arXiv, 2015, 1507.01012

10A.S.Mishchenko.StochasticOptimizationforAnalyt-icalContinuation:WhenaprioriKnowledgeisMissing, 14thchapterinCorrelatedElectrons:FromModelstoMaterials.ed.byE.Pavarini,W.Koch,F.AndersandM.Jarrell,VerlagdesForschungszentrumJülich, 2012: 1～24

11A.W.Sandvik.Stochasticmethodforanalyticcontinu-ationofquantumMonteCarlodata.Phys.Rev.B,1998, 57:10287

ExplorationontheTeachingReformofAnalyticContinuationCourse——AndTalkingabouttheMaximumEntropyMethod

LvJianping

(DepartmentofPhysics,AnhuiNormalUniversity,Wuhu,Anhui241000)

For the analytic continuation part in Mathematical Physics course which is more or less abstract to students, we design the course teaching based on numerical simulation methods. In this paper, via the construction of physical model, we introduce the basic aspects for linear response theory and maximum entropy analytic continuation method. We design the specific procedure in course teaching process, and demonstrate the numerical results for a specific example. Finally, we discuss the possible directions to improve present course teaching process.

Mathematical Physics; analytic continuation; maximum entropy method

*國家自然科學基金，項目編號：11405003,11147013

呂建平(1983- )，男，博士，主要從事數學物理方法、群論和大學物理等課程的教學，以及凝聚態物理理論研究.

2016-06-19)