含間隙RU-RPR解耦并聯機構混沌與沖擊現象

侯雨雷， 汪 毅， 井國寧， 曾達幸， 邱雪松， 李慧劍

(1. 燕山大學 機械工程學院，河北 秦皇島 066004；2.燕山大學 河北省重型裝備與大型結構力學可靠性重點實驗室，河北 秦皇島 066004)

含間隙RU-RPR解耦并聯機構混沌與沖擊現象

侯雨雷1， 汪 毅1， 井國寧1， 曾達幸1， 邱雪松1， 李慧劍2

(1. 燕山大學 機械工程學院，河北 秦皇島 066004；2.燕山大學 河北省重型裝備與大型結構力學可靠性重點實驗室，河北 秦皇島 066004)

針對含間隙機構中的混沌與沖擊現象，以自主提出的RU-RPR(R為轉動副，U為虎克鉸，P為移動副)兩轉動解耦并聯機構為研究對象，考慮運動副間隙，結合Lankarani-Nikravesh接觸力模型與拉格朗日方程建立間隙機構動力學模型，分析不同的驅動速度和摩擦因數對機構中混沌現象與沖擊的影響，同時探討機構的穩定性與沖擊現象的關系，并分析增設彈簧對機構動力學特性的影響。研究結果表明，改變驅動速度與摩擦因數時，沖擊現象仍然存在，而機構可以由混沌運動變為周期運動，穩定性增強；機構的穩定性與沖擊現象并沒有必然的聯系，且增加彈簧可以顯著的減弱機構中的沖擊程度。

并聯機構；間隙；動力學；混沌；沖擊

隨著機械產品日益朝著高速、重載、高精度的目標發展，對機構動態性能的要求也越來越高，而不可避免的運動副間隙的影響愈發引起眾多學者和工程界的重視。并聯機構的獨特優勢及其廣泛應用已為業界認可，作為多維的強非線性系統，并聯機構包含著豐富的動力學特性，其能否適應更高的作業條件要求而繼續得以應用并發展，將取決于動力學這一關鍵問題的解決程度。

目前，很多學者對含間隙機構的動力學建模[1-2]、動態特性[3-6]、混沌現象[7-10]、實驗分析[11]等，已經進行了深入而廣泛的研究。時兵等[12]針對大型重載機構虛擬樣機中的間隙旋轉鉸，基于間隙矢量模型對一汽輪機閥門機構進行仿真計算，分析鉸間隙、制造和裝配誤差等因素對機構動力學特性的影響。BAI等[13]采用一種混合接觸力模型分析含間隙機構的磨損。RAHMANIAN等[8]繪制了含間隙曲柄滑塊機構隨間隙尺寸變化的分岔圖。魏曉輝等[14]分析了裝配間隙對起落架收放機構的影響，并提出了改進設計。余躍慶等[15]針對運動副間隙引起的并聯機器人定位誤差，探討了運動副間隙誤差引起的系統結構誤差的變化規律，并提出優化補償方法。趙剛練等[16]研究了含空間圓柱副間隙的動力學建模方法，并分析了圓柱副間隙對其他構件的動態特性的影響。王庚祥等[17]對含空間球面副間隙對新型減振平臺4-SPS/CU并聯機構動力學性能影響進行研究，分析球面副間隙對該并聯機構運動學特性及驅動力的影響。趙寬等[18]分析了含間隙的曲柄滑塊機構在考慮運動副間隙、摩擦力及系統參數具有隨機性時的動力響應問題。

混沌是非線性動力系統所特有的且普遍存在的現象，混沌現象在有些情況下于機構性能有利，而在有些情況下將產生不良的影響，導致本來認為無論如何是安全和穩定的系統失靈，為工程系統的響應和可靠性增加了不確定因素。對并聯機構進行混沌現象辨識，進而體現于動態設計中并實現有效的控制，對機構動態特性的優劣具有關鍵性的作用。

在間隙機構中，運動副元素之間的分離碰撞將產生沖擊現象，嚴重的沖擊會導致機構的運動精度降低，加劇磨損，對機構產生破壞，降低機構的使用壽命。現有的文獻中，含間隙機構動態性能的分析已經比較普遍，而針對引起間隙機構動態性能惡化的沖擊現象卻鮮有學者進行深入的研究。

機構的穩定性是指機構保持原有運動狀態的能力。當給定機構的驅動為周期性時，如果機構處于周期運動狀態，則機構是穩定的，而如果機構處于混沌運動狀態，則機構是不穩定的。運動副的間隙會造成機構運動的不確定性，機構的動態特性在某種條件下會劇烈地變化，而且呈現出混沌特性[19]。OLYAEI等[19]通過某種控制方法使機構由混沌狀態變成不混沌狀態，從而使機構由不穩定狀態變成穩定狀態。ZHANG等[4]對含多間隙的平面并聯機構進行動力學建模，分析了載荷、運動速度和運動軌跡對機構穩定性的影響。王威等[20]以平面四桿機構為例研究了間隙與干摩擦對機構運行穩定的影響。

本文即在此背景下，以含間隙RU-RPR解耦并聯機構[21]為研究對象，利用Lankarani-Nikravesh接觸力模型計算法向接觸力，將修正的Coulomb摩擦力法則嵌入到切向接觸力的計算過程中，應用拉格朗日方程建立間隙機構動力學模型，采用變步長四階龍格庫塔法予以數值求解，辨識解耦并聯機構非線性動力學中的混沌現象，分析不同的因素對機構中混沌與沖擊現象的影響，探討機構的穩定性與混沌現象間關系，并分析增設彈簧對機構沖擊現象的影響，以期對并聯機構動力學研究有所深化，為研制高效、高速和穩定的并聯裝備提供理論依據與技術支撐。

1 轉動副間隙中的接觸力分析

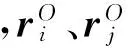
(1)

其單位矢量為

n=e/e

(2)

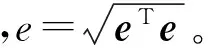
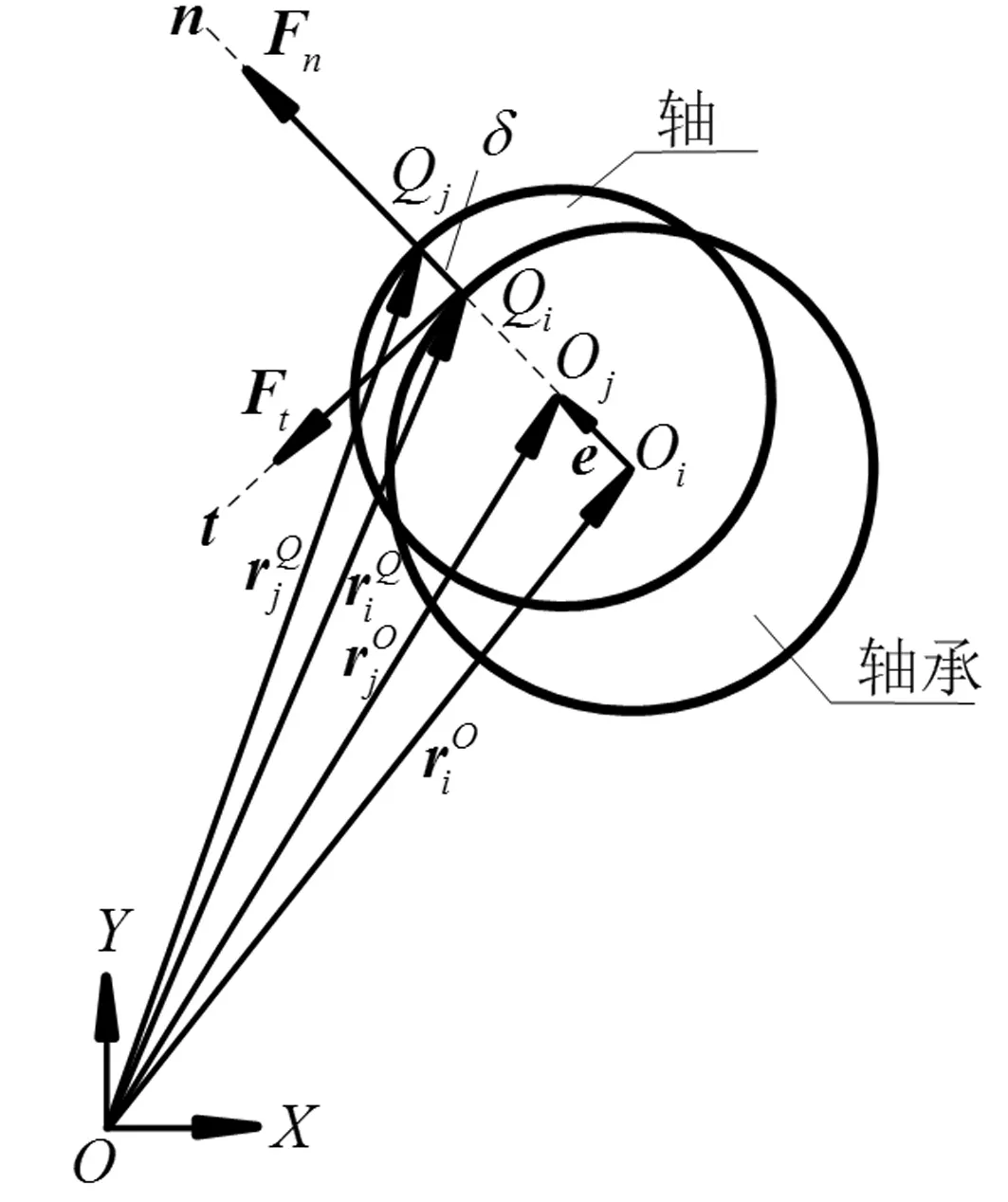
圖1 轉動副間隙模型Fig.1 Gap model of the rotation pair

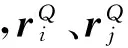
(3)

式中:Ri、Rj分別為軸承與軸的半徑。

式(3)兩邊對時間求導，可得碰撞點速度為

(4)

將碰撞點的相對速度投影到碰撞平面的切向和法向平面，可得相對的法向速度vn和切向速度vt，其標量形式為

(5)

式中:切向矢量t可以通過將n逆時針旋轉90°獲得。

軸承和軸的穿透深度為

δ=e-c

(6)

式中:c為半徑間隙，且c=Ri-Rj。當δ為正值時，軸承與軸接觸，反之，軸承與軸沒有接觸。

碰撞過程中必然產生碰撞力，導致一定的沖擊、振動，從而對機構的性能造成不利影響。因此，采用一種合適的接觸力模型來估算碰撞過程中的碰撞力非常重要。本文選用Lankarani-Nikravesh接觸力模型[22]，該模型既考慮了碰撞過程中的能量損失，又較全面地考慮了碰撞體的材料屬性、局部彈性變形以及碰撞速度等信息[23]，廣泛用于含間隙機構的動力學分析。軸對軸承的法向接觸力的表達式為

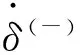
(8)

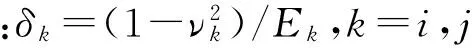
(9)

式中:cf為摩擦因數；v0、v1為給定的速度界限。

該法則可以防止切向接觸力的方向突變，從而有利于數值積分的穩定。

軸對軸承的碰撞力可表示為

(10)

式中: fix、fiy分別為軸對軸承的碰撞力在X方向和Y方向上的分量。

2 含間隙RU-RPR解耦并聯機構動力學建模

2.1 RU-RPR解耦并聯機構組成

RU-RPR兩轉動解耦并聯機構如圖2所示，該機構由定平臺、動平臺以及連接兩平臺的兩條支鏈組成，從定平臺到動平臺，第一條分支鏈依次由轉動副和虎克鉸相連，第二條分支鏈依次由轉動副、移動副和轉動副相連。其中，第二條分支中移動副的移動方向垂直于該分支兩個轉動副的軸線，兩分支中與固定平臺相連的兩轉動副軸線相互平行且與虎克鉸的一條軸線平行，虎克鉸的另一條軸線與第二分支中與動平臺相連的轉動副軸線重合。

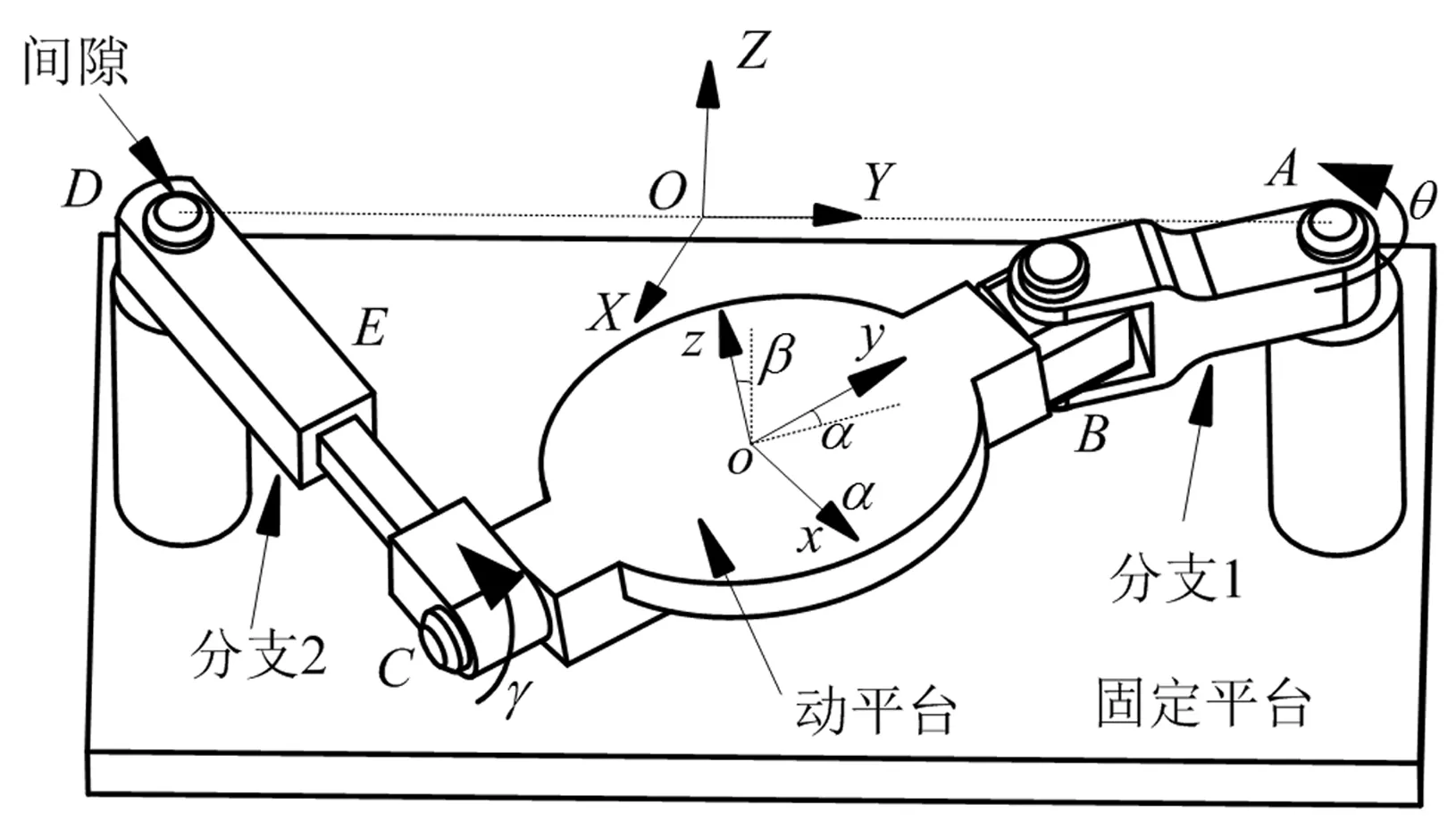
圖2 RU-RPR兩轉動并聯機構組成示意圖Fig.2 Composition schematic of RU-RPR 2-DOF rotational parallel mechanism

在定平臺上固連定坐標系O-XYZ，其中，坐標原點O為與連線中點在定平臺平面的投影，Z軸豎直向上，Y軸與和定平臺相連的兩轉動副A、D軸線垂直并指向A；在動平臺上固連動坐標系o-xyz，其中，坐標原點o建立在動平臺幾何中心，y軸和分支2中與動平臺相連的轉動副的軸線共線，方向指向虎克鉸，z軸與動平臺平面垂直，方向向上。機構處于初始位置時，AB與BC共線。

以RU-RPR并聯機構第一分支的轉動副A和第二分支與動平臺相連的轉動副C作為主動副，θ與γ分別表示轉動副A、轉動副C的旋轉角度；α與β分別表示動平臺繞動坐標系的z軸和y旋轉角度。

θ、γ為輸入角度，而α和β為輸出角度。顯見，θ與α一一對應，而γ與β也是一一對應關系，所以，RU-RPR并聯機構繞y軸和z軸的兩轉動自由度即兩轉動互不影響。因此，在研究轉動副D處的間隙時，可暫不考慮機構繞y軸的轉動，而只考慮動平臺繞z軸(鉛垂方向)的轉動，故可將RU-RPR解耦并聯機構視作一個平面四桿機構，其等效機構簡圖如圖3所示。

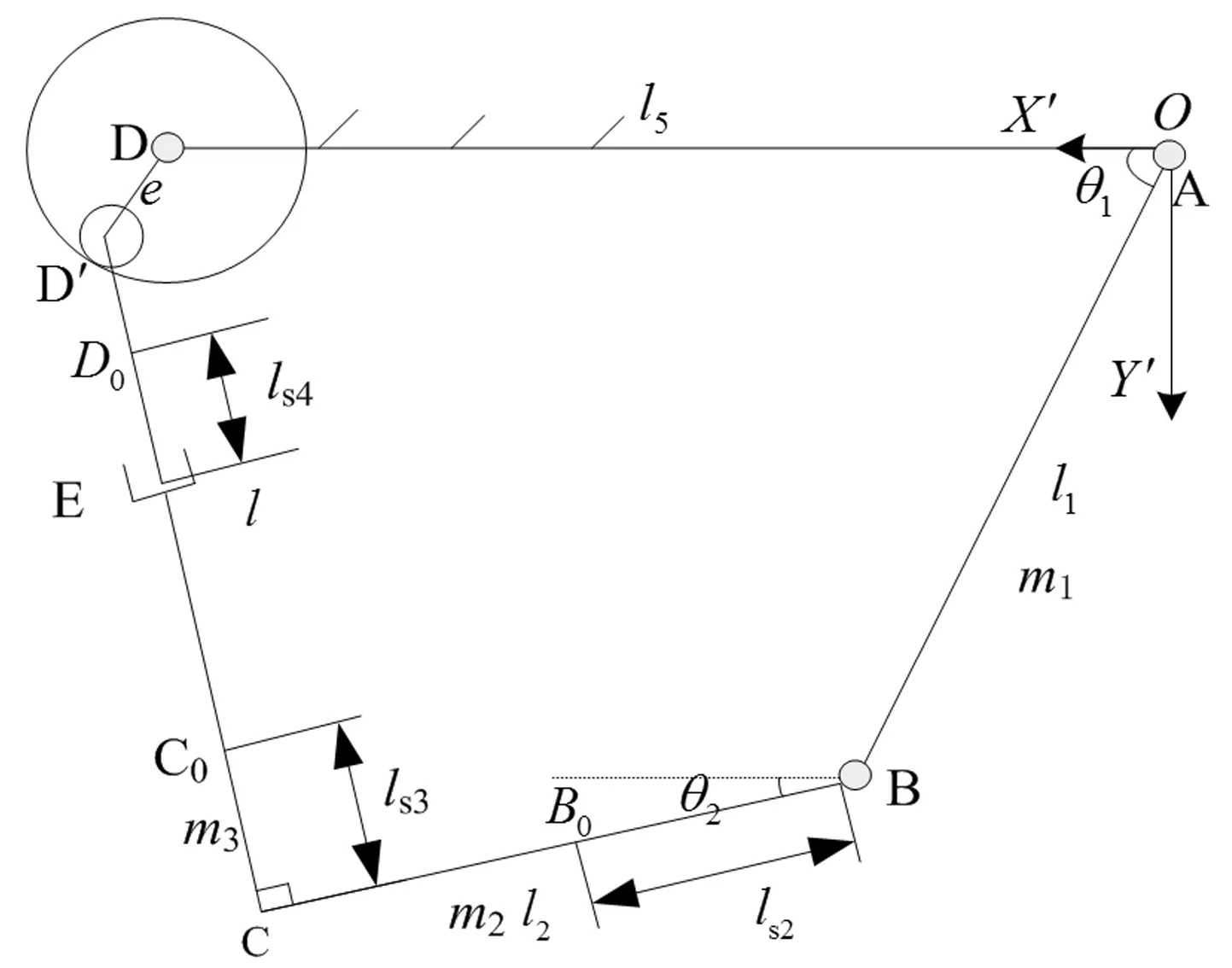
圖3 含間隙RU-RPR并聯機構等效機構簡圖Fig.3 Schematic diagram of equivalent agencies of RU-RPR parallel mechanism with clearance

2.2 含間隙RU-RPR并聯機構運動分析

如圖3所示，針對等效的含間隙RU-RPR解耦并聯機構建立平面坐標系X′O′Y′，并對后續動力學分析所需相關參數定義如下：l1、θ1、J1分別表示桿AB的長度、轉角以及對轉動連接副A的轉動慣量；l2、ls2、θ2、m2、Js2分別表示桿BC的長度、質心B0距運動副B的距離、轉角(與X′軸正向的夾角)、質量以及對自身質心的轉動慣量；m3、ls3、Js3分別表示桿CE的質量、質心C0與C之間的距離以及對自身質心的轉動慣量；m4、ls4、Js4分別表示桿DE的質量、質心D0距運動副E的距離以及對自身質心的轉動慣量；l表示CD之間的距離，l5表示機架的長度；x,y分別表示間隙(圖中小圓表示軸，大圓表示軸承)的橫向、縱向分量，即軸和軸承間的橫向、縱向相對位移分量。

由于間隙的存在，此時該四桿機構有三個自由度。設定機構的廣義坐標為：桿AB的轉動角度θ1，軸銷與軸承橫向相對位移x，軸銷與軸承的縱向相對位移y。通過引進擾動坐標，建立含間隙解耦并聯機構的運動學模型。

對無間隙四桿機構，有如下的封閉方程

(11)

式中:θ20為無間隙機構中BC桿轉角，l0為無間隙機構中CD桿的長度，cθ1=cosθ1，sθ1=sinθ1，其余類似。

對D處含一個間隙的四桿機構，有如下封閉方程

(12)

利用擾動坐標法，含間隙機構的轉角均由無間隙機構的轉角加上一個小擾動角構成，桿長度由無間隙機構的長度加上一個小的擾動長度構成。于是有

(13)

將式(13)代入式(12)中，根據三角公式和等價無窮小概念化簡，可得

(14)

聯立式(11)和式(14)，得

(15)

則式(15)可簡化為

(16)

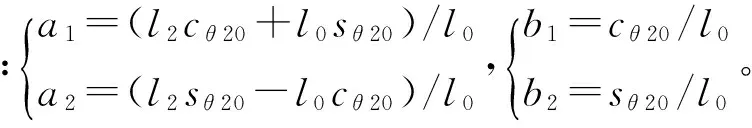
整個RU-RPR并聯機構的動能T及勢能V分別為

(17)

式中:F=Js2+m2ls22+Js3+m3l22+Js4+m3ls32+m4ls42，G=m3l1l2+m2l1ls2。

拉格朗日函數為

L=T-V

(18)

進而，拉格朗日運動方程可表示為

(19)

式中:Qj表示非保守系統中對應廣義坐標qj的廣義力，可以表示為

(20)

式中:Fi和Mi分別為作用在物體i質心的外力、外力矩，ri、φi分別為物體i質心的移動位移和轉動角度。

在小學數學教學中培養學生的自主學習能力，需要加強對數學課程的策略改革，創新教學方式，激發學生的學習興趣，促使學生積極進行學習活動，鼓勵學生進行自主學習，提高學生的自主學習能力，促進學生素質能力的培養。

由式(20)，廣義力可以表示為

(21)

將式(18)、式(21)代入式(19)，可得

(22)

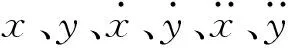
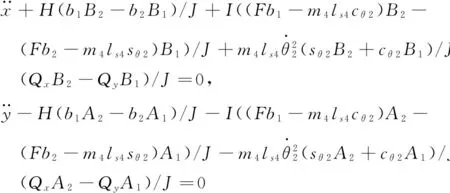
(23)

式中:

3 含間隙RU-RPR并聯機構動力學數值仿真

機構中軸承與軸之間存在碰撞與非碰撞兩種狀態，而在分析每次碰撞的初始碰撞速度及碰撞面的方向時，精確的檢測出碰撞點至關重要。已知軸承與軸發生碰撞的條件為

δ(tn)δ(tn+1)≤0

(24)

則在時間間隔tn與tn+1之間至少發生一次碰撞。碰撞時間非常短暫，故為保證計算效率與精度，采用變步長四階龍格庫塔法進行數值積分，當碰撞深度大于積分誤差時，積分步長設定為前一個步長的一半，重新計算直至滿足誤差要求，本文借鑒文獻[25]中的方法來控制步長。

式(23)包含兩個二階非線性方程，采用變步長四階龍格庫塔法予以求解。機構桿件形狀參見圖2，多選用長方形和圓柱形，其材料為45鋼，則可得到RU-RPR機構相關參數如下：

l1=130 mm，l2=308 mm，ls2=154 mm，ls3=80 mm，ls4=54 mm，l5=524 mm，J1=7.351×10-3kg·mm3，Js2=6.160×10-2kg·mm3，Js3=5.772×10-3kg·mm3，Js4=3.008×10-3kg·mm3，m2=8.516 kg，m3=1.161 kg，m4=1.405 kg。

機構動力學仿真參數如表1所示，機構初始時桿OB與桿BC共線，機構驅動角速度為ω=10π rad/s。選取計算了2個周期的仿真結果，機構碰撞深度、接觸力和軸心軌跡分別如圖4(a)、圖4(b)和圖4(c)所示；圖4(d)為機構Poincare映射圖，計算了500個映射點。Poincare映射[8]可以方便地進行混沌辨識。Poincare映射上的一個點及少數離散點、閉合曲線、成片的具有分形結構的密集點分別表示系統的周期運動、擬周期運動和混沌運動。

圖4(a)為軸承與軸之間的穿透深度，由圖4(a)可知，軸與軸承在分離和碰撞之間不斷變換，并非處于連續接觸的狀態。圖4(c)中軸心軌跡圖也可體現該特點(其中虛線圓表示軸承邊界，該圓以軸承為中心為圓心，以軸承半徑為半徑)。軸與軸承在不斷的分離與碰撞過程中，必然產生沖擊現象，而圖4(b)中高頻振蕩的接觸力曲線也印證了此現象，且圖4(a)中穿透深度振蕩的時間點與圖4(b)中接觸力振蕩的時間點是一致的。圖4(d)中間隙處相對位移x與相對位移y的Poincare映射為具有一定的規律的密集點，表現為混沌狀態。

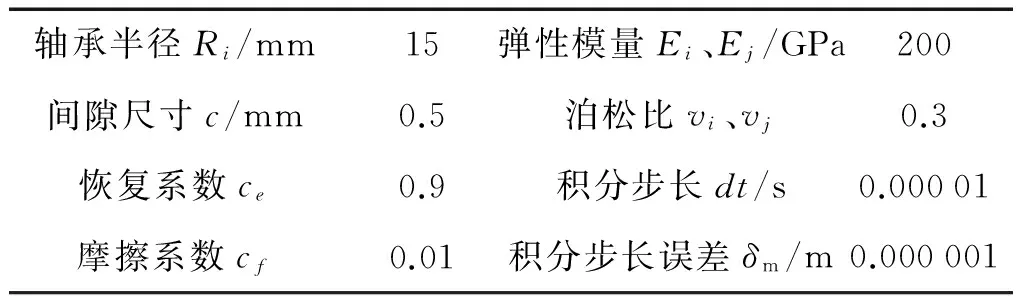
表1 RU-RPR并聯機構動力學仿真參數

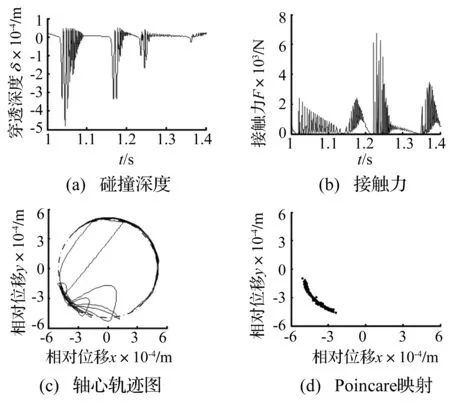
圖4 含間隙RU-RPR并聯機構的動力學響應Fig.4 Dynamic responses of RU-RPR parallel mechanism with clearance

4 RU-RPR并聯機構動力學特性參數影響分析

驅動速度以及摩擦因數是影響機構動態性能的重要因素。如下將根據接觸力、軸心軌跡以及Poincare映射分析不同的驅動速度及不同的摩擦因數對機構中沖擊現象的影響，同時探討機構穩定性與沖擊現象的相互關系。

首先依據表1所列參數，參照前述仿真方法，依次取驅動速度為2π rad/s、8π rad/s、20π rad/s、40π rad/s，所得相應的機構接觸力、軸心軌跡及Poincare映射分別如圖5～圖7所示。

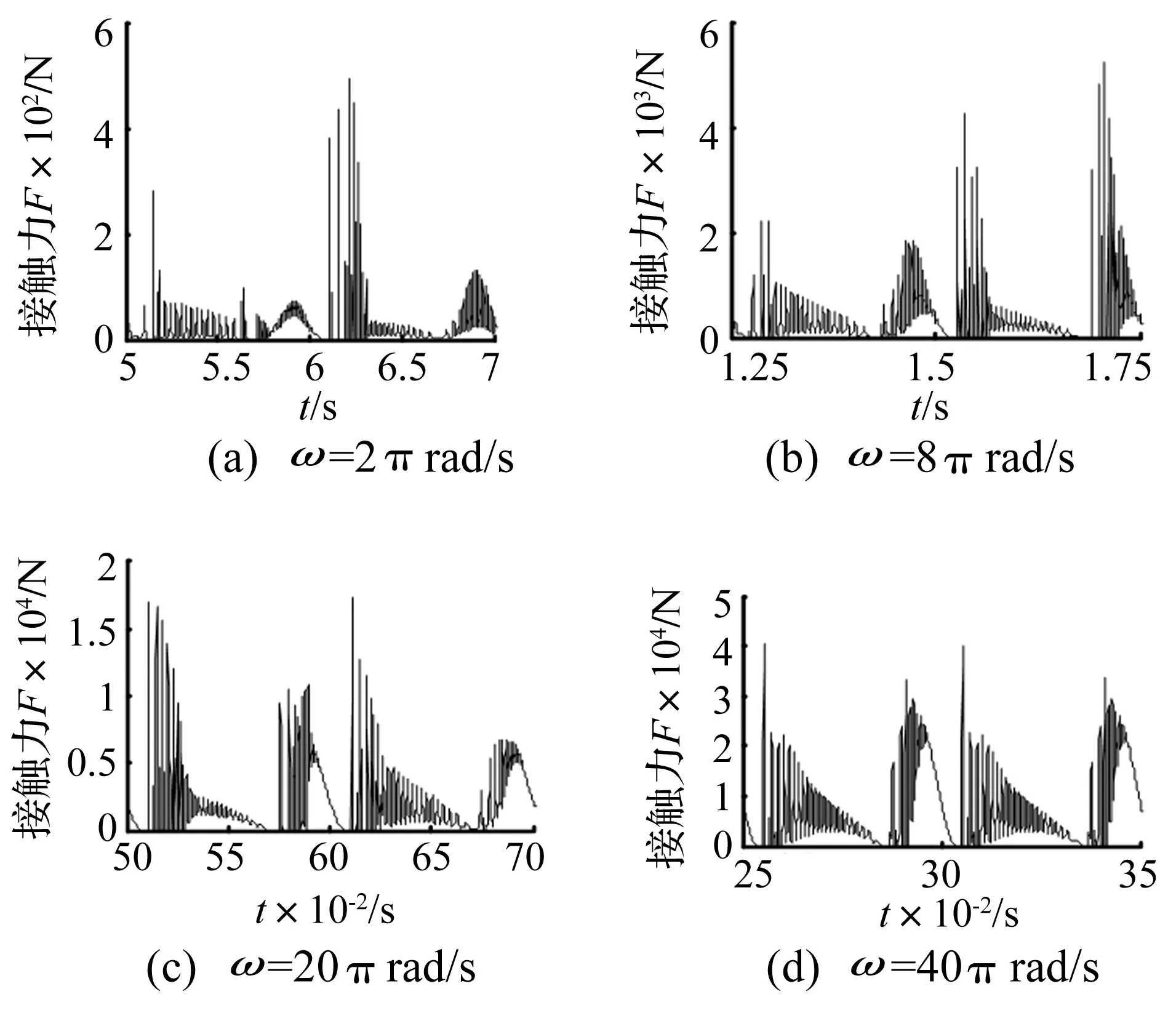
圖5 不同驅動速度下RU-RPR機構的接觸力Fig.5 Contact forces of RU-RPR mechanism at different driving speeds

由圖5可看出，隨著驅動速度的增加，接觸力曲線的峰值增大，意味著隨著驅動速度的增大，軸與軸承之間的穿透深度更大，軸與軸承之間的沖擊現象更嚴重，圖6也體現了該特點。

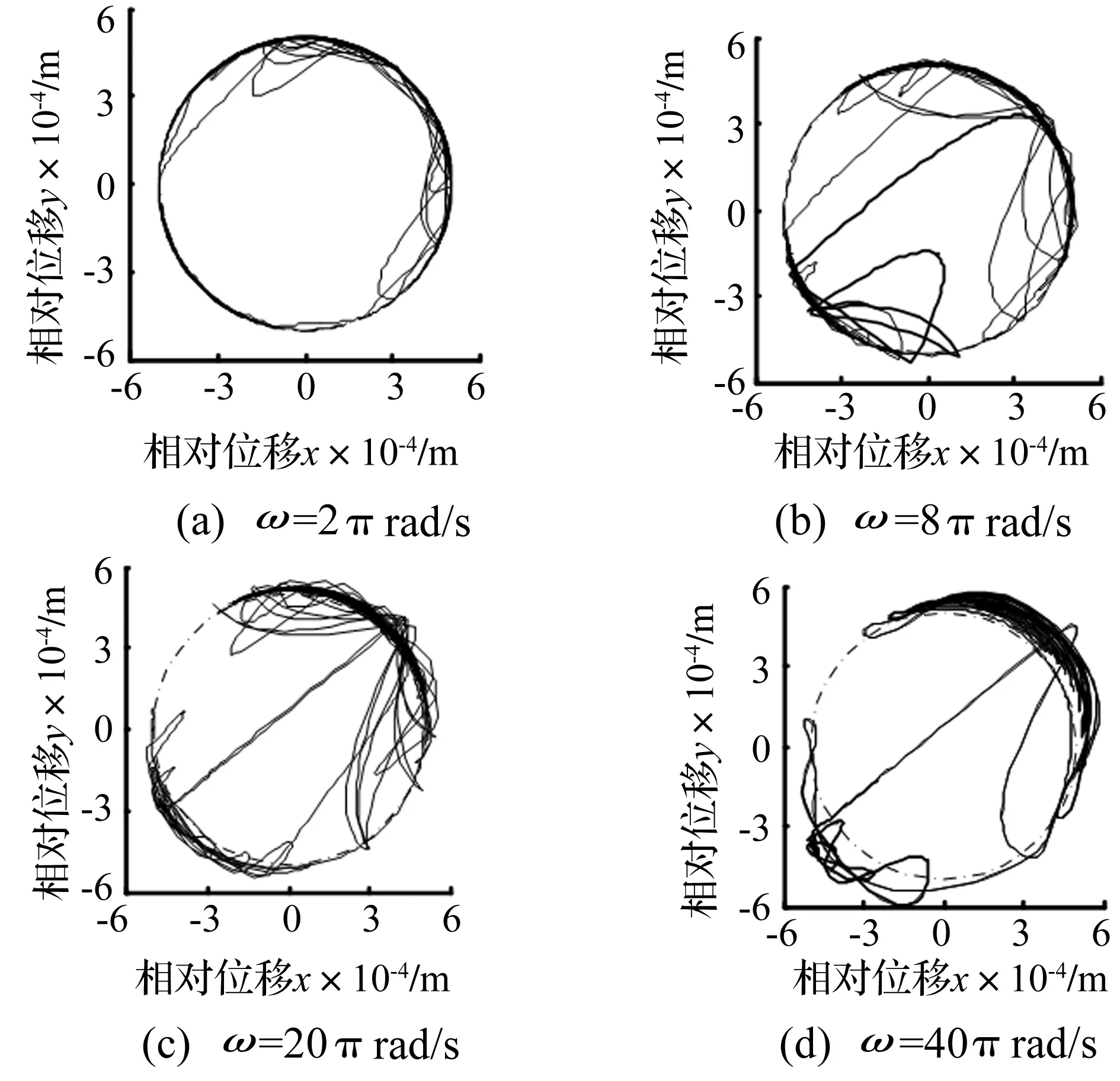
圖6 不同驅動速度下RU-RPR機構的軸心軌跡圖Fig.6 Axle center trajectory diagrams of RU-RPR mechanism at different driving speeds

圖7表明，隨著驅動速度的增大，機構中的混沌現象減弱，甚至形成周期運動，機構的穩定性增強。而圖6顯示出在各種驅動速度下，軸與軸承之間始終無法在整個運動階段連續接觸，即沖擊現象依然存在。由此說明機構的穩定性與沖擊現象并沒有必然的聯系。

其次，令驅動速度為5πrad/s，按摩擦系數依次取0.01、0.02、0.05、0.1四種情況，分析機構接觸力、軸心軌跡及Poincare映射分別如圖8～圖10所示。

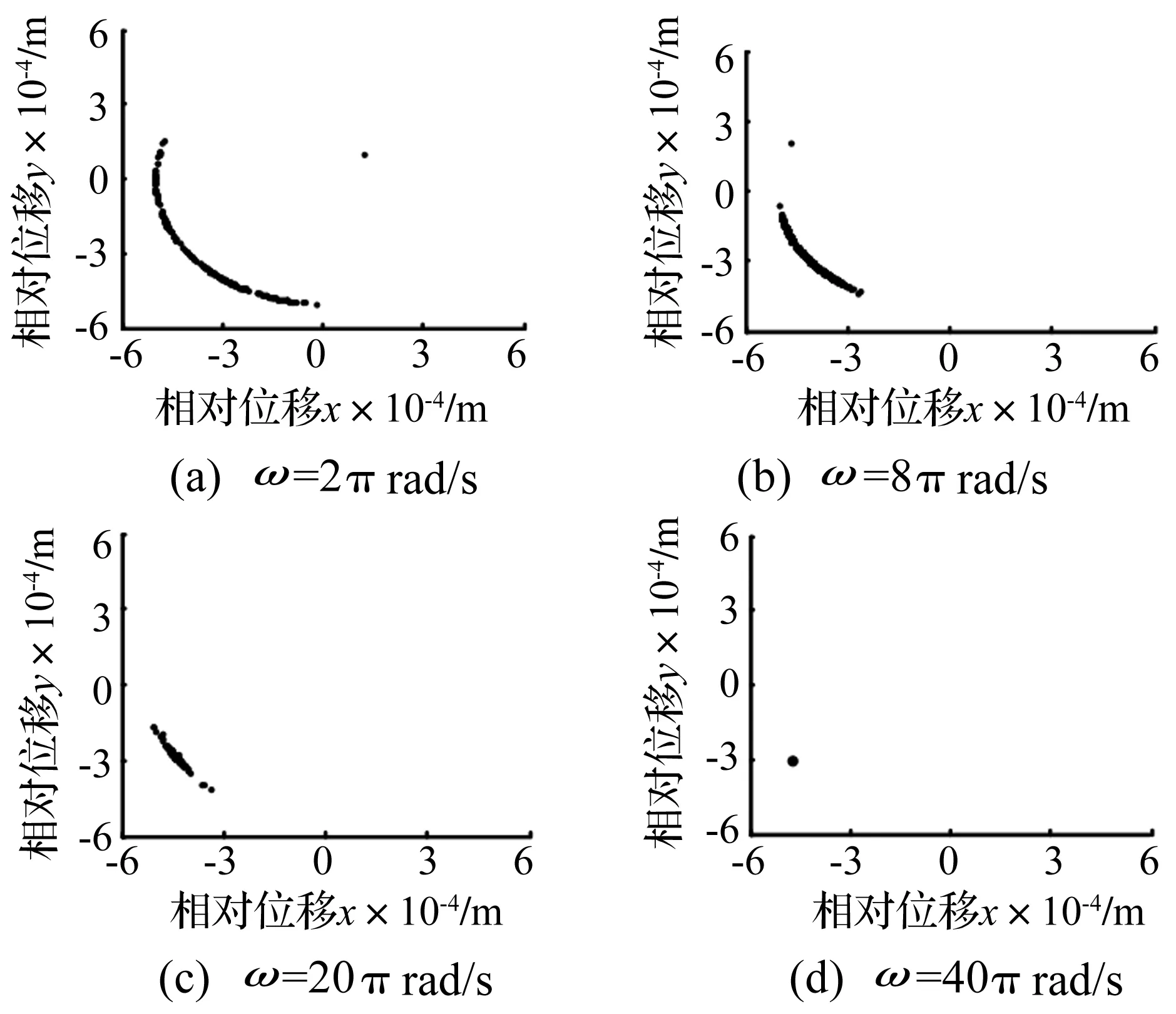
圖7 不同驅動速度下RU-RPR機構的Poincare映射Fig.7 Poincare mapping diagrams of RU-RPR mechanism at different driving speeds

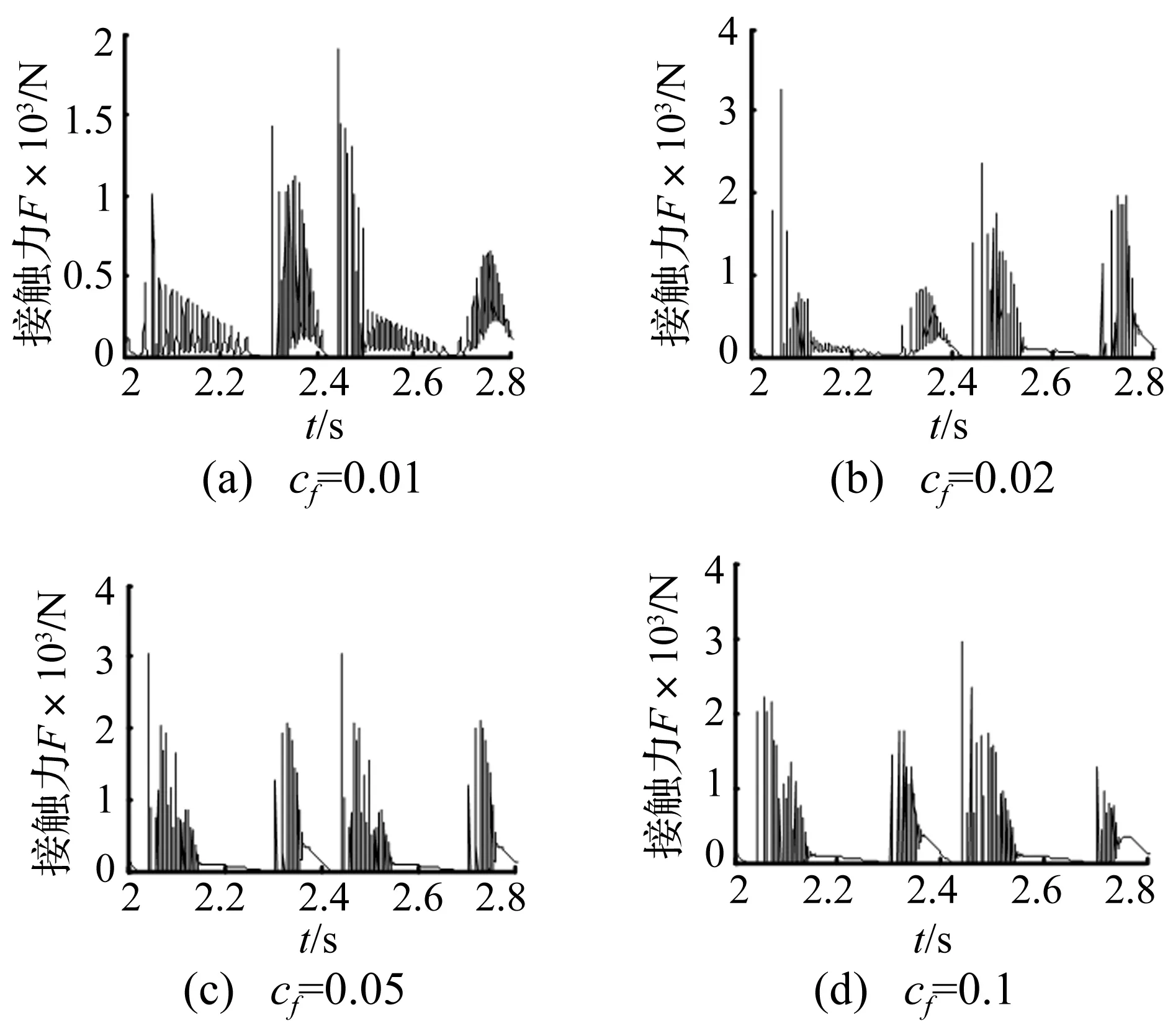
圖8 不同摩擦系數下RU-RPR機構的接觸力Fig.8 Contact forces of RU-RPR mechanism at different friction coefficients

由圖8可知，當摩擦系數比較小時，接觸力的峰值隨著摩擦系數的增大而增大，沖擊現象更為嚴重；而當摩擦系數較大時，隨著摩擦系數增大，接觸力的峰值幾乎不變，沖擊現象的程度基本保持穩定。

圖10表明，摩擦系數越大，機構中的混沌現象越弱，機構的穩定性增強；但是軸與軸承之間的沖擊碰撞依然存在(參見圖9)，也再次說明機構的穩定性與沖擊現象間并不存在必然的聯系。

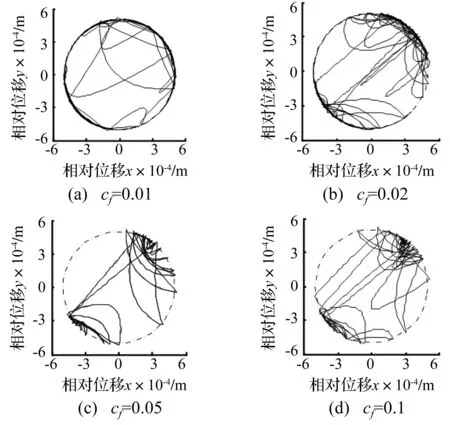
圖9 不同摩擦系數下RU-RPR機構的軸心軌跡圖Fig.9 Axle center trajectory diagrams of RU-RPR mechanism at different friction coefficients

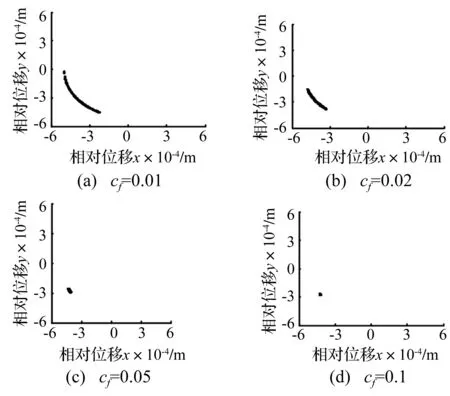
圖10 不同摩擦系數下RU-RPR機構的Poincare映射Fig.10 Poincare mapping diagrams of RU-RPR mechanism at different friction coefficients

5 RU-RPR并聯機構間隙影響的控制

根據RU-RPR并聯機構動態特性參數影響分析，隨著驅動速度或摩擦系數的增大，機構中的混沌現象減弱，機構的穩定性增強，但軸與軸承之間始終無法連續接觸，沖擊現象依然存在，甚至更加嚴重，而這必將降低機構的精度、壽命等，影響其正常工作。

故此，為減少軸與軸承之間的沖擊，考慮在桿DE的質心與機架OD的幾何中心之間增加一個彈簧，如圖11所示。設彈簧原長為Ls0，剛度系數為ks，伸長后彈簧長度為Ls，則增加彈簧后RU-RPR機構的勢能為

(25)

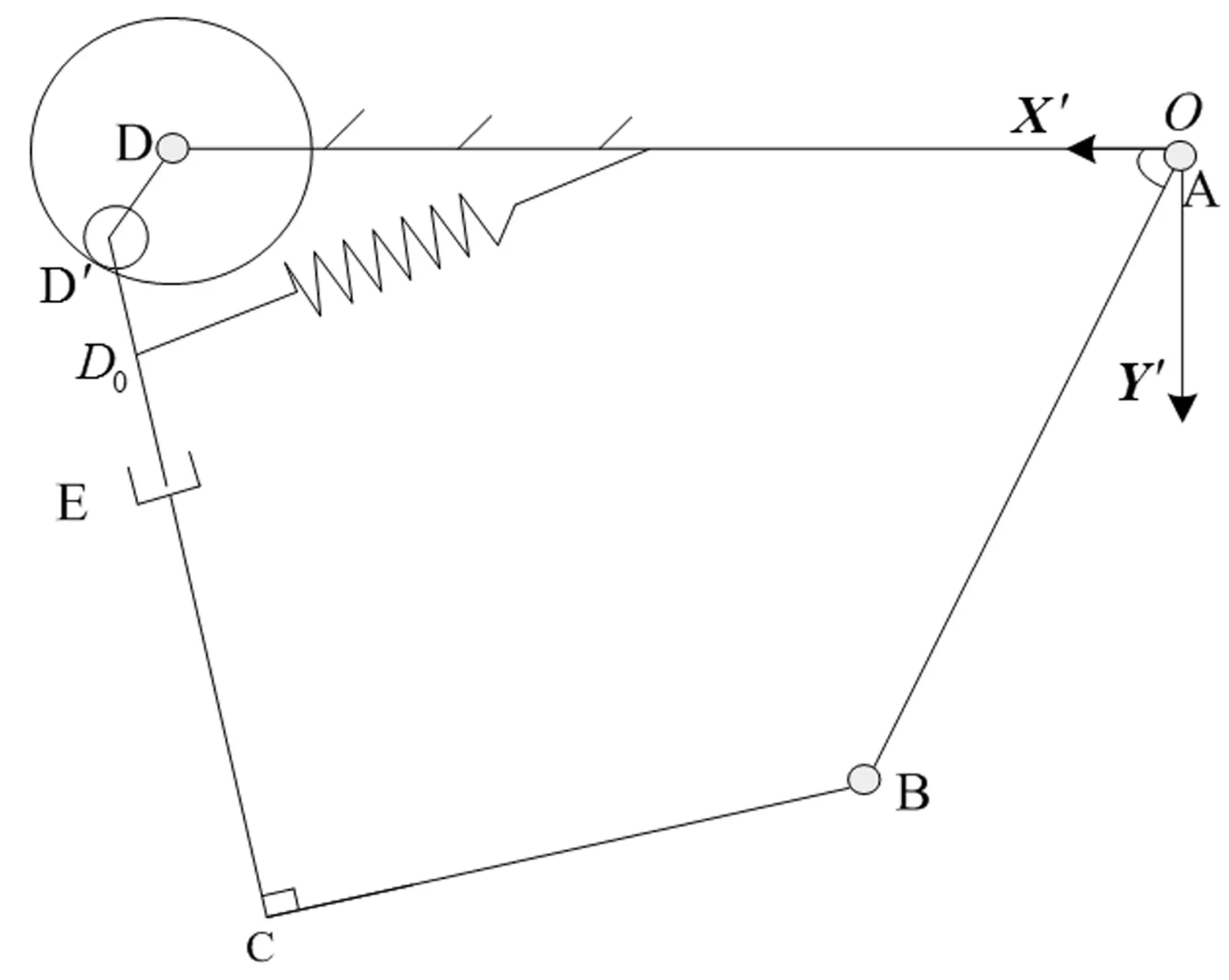
圖11 增加彈簧后的RU-RPR機構簡圖Fig.11 RU-RPR mechanism diagram after adding the spring

為了達到預期的效果，使彈簧始終處于拉伸狀態，且設定彈簧的原長為0.15 m，剛度系數為1 000 N/m，驅動速度ω=10π rad/s，其它動力學參數參照表1，仿真結果如圖12所示。由圖12(a)可知，增加彈簧后，軸與軸承之間始終連續接觸，沒有發生沖擊現象，圖12(b)、(c)也說明該特點。此外，對比圖12(b)與圖4(b)可知，增加彈簧后，接觸力波動趨于平緩，且最大值由6 778降為1 629，降低了76%。圖12(d)則表明增加彈簧后，機構中的混沌現象消失。

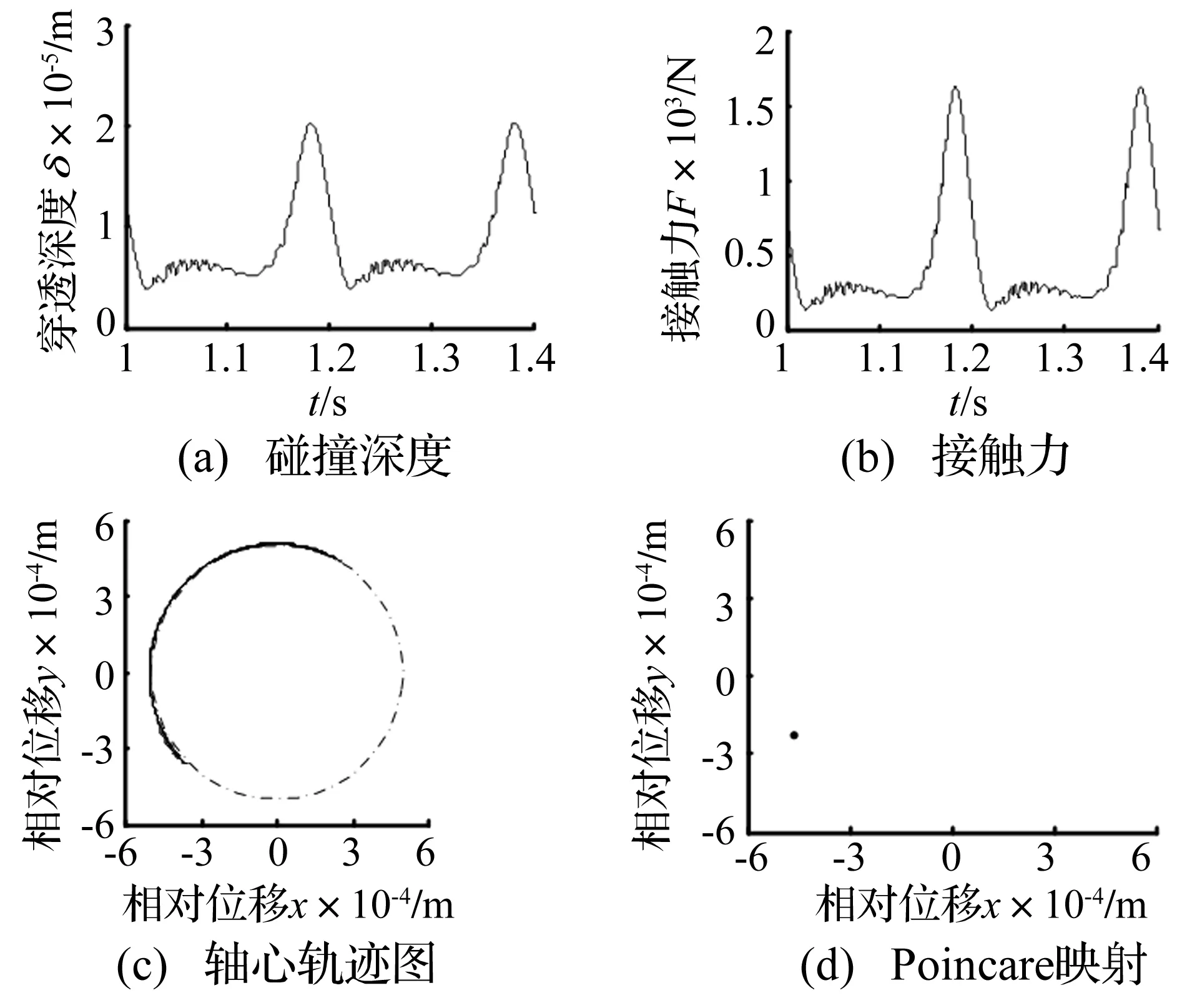
圖12 增設彈簧后RU-RPR并聯機構的動力學響應Fig.12 Dynamic responses of RU-RPR parallel mechanism after adding spring

6 結 論

(1)利用Lankarani-Nikravesh接觸力模型、修正的Coulomb摩擦力法則和拉格朗日方程建立了含間隙RU-RPR解耦并聯機構的動力學模型，借助變步長四階龍格庫塔法予以求解，動力學仿真結果表明RU-RPR機構轉動副中間隙的存在使得機構在某種條件下存在混沌和沖擊現象。

(2)當含間隙RU-RPR機構中驅動速度、摩擦系數增大時，機構由混沌運動變為周期運動，即機構的穩定性提高，而沖擊現象依然存在，說明機構的穩定性與沖擊現象并沒有必然的聯系，且通過增加彈簧并預緊能夠有效消除機構中的沖擊現象，對高可靠性并聯裝備的設計與控制具有一定的理論參考意義和實踐應用價值。

[ 1 ] 白爭鋒. 考慮鉸間間隙的機構動力學特性研究[D]. 哈爾濱：哈爾濱工業大學，2011.

[ 2 ] FLORES P. Dynamic analysis of mechanical systems with imperfect kinematic joints[D].Portugal: Universidade Do Minho, 2004.

[ 3 ] 王庚祥，劉宏昭. 考慮球面副間隙的4-SPS/CU并聯機構動力學分析[J]. 機械工程學報，2015, 51(1): 43-51. WANG Gengxiang, LIU Hongzhao. Dynamics analysis of 4-SPS/CU parallel mechanism with spherical joint clearance[J]. Journal of Mechanical Engineering, 2015, 51(1): 43-51.

[ 4 ] ZHANG Xuchong, ZHANG Xianmin, CHEN Zhong. Dynamic analysis of a 3-RRR parallel mechanism with multiple clearance joints[J]. Mechanism and Machine Theory, 2014, 78(8): 105-115.

[ 5 ] 白爭鋒, 趙陽, 趙志剛. 考慮運動副間隙的機構動態特性研究[J]. 振動與沖擊, 2011, 30(11): 17-20. BAI Zhengfeng, ZHAO Yang, ZHAO Zhigang. Dynamic characteristics of mechanisms with joint clearance[J]. Journal of Vibration and Shock, 2011, 30(11): 17-20.

[ 6 ] 張增磊, 巫世晶, 趙文強, 等. 含間隙高速多連桿傳動機構動力學特性研究[J]. 振動與沖擊, 2014, 33(14): 66-71. ZHANG Zenglei, WU Shijing, ZHAO Wenqiang, et al. Dynamic characteristics of high-speed multi-link transmission mechanisms with clearance[J]. Journal of Vibration and Shock, 2014, 33(14): 66-71.

[ 7 ] 侯雨雷，汪毅，李明洋，等.一種含間隙兩轉動一移動解耦并聯機構混沌現象辨識[J]. 中國機械工程，2015, 26(13): 1759-1766. HOU Yulei, WANG Yi, LI Mingyang, et al. Chaos identification of two rotational and one translational decoupled parallel mechanism concerning clearance[J]. China Mechanical Engineering, 2015, 26(13): 1759-1766.

[ 8 ] RAHMANIAN S, GHAZAVI M R. Bifurcation in planar slider-crank mechanism with revolute clearance joint[J]. Mechanism and Machine Theory, 2015, 91(5): 86-101.

[ 9 ] TANG Yuanguang, CHANG Zongyu, DONG Xiaogang, et al. Nonlinear dynamics and analysis of a four-bar linkage with clearance[J]. Frontiers of Mechanical Engineering, 2013, 8(2): 160-168.

[10] 何文運, 張俊紅, 馬梁. 剪式齒輪傳動機構非線性動力學特性研究[J]. 振動與沖擊, 2015, 34(15): 115-121. HE Wenyun, ZHANG Junhong, MA Liang. Nonlinear dynamic characteristics of a scissor gear transmission system[J]. Journal of Vibration and Shock, 2015, 34(15): 115-121.

[11] ERKAYA S, DOGAN S, ULUS S. Effects of joint clearance on the dynamics of a partly compliant mechanism:Numerical and experimental studies[J]. Mechanism and Machine Theory, 2015, 88(2): 125-140.

[12] 時兵，金燁. 面向虛擬樣機的機構間隙旋轉鉸建模與動力學仿真[J]. 機械工程學報，2009, 45(4): 299-303. SHI Bing, JIN Ye. Dynamic simulation and modeling of revolute clearance joint for virtual prototyping[J]. Journal of Mechanical Engineering, 2009, 45(4): 299-303.

[13] BAI Zhengfeng, ZHAO Yang, CHEN Jun. Dynamics analysis of planar mechanical system considering revolute clearance joint wear[J]. Tribology International, 2013, 64(3): 85-95.

[14] 魏小輝, 王鈺龍, 印寅, 等. 某起落架收放聯動機構故障分析及改進設計[J]. 中國機械工程，2014, 25(3): 399-403. WEI Xiaohui, WANG Yulong, YIN Yin, et al. Failure analysis and improved design of a landing gear retraction mechanism[J]. China Mechanical Engineering, 2014, 25(3): 399-403.

[15] 余躍慶, 田浩. 運動副間隙引起的并聯機器人誤差及其補償[J]. 光學精密工程，2015, 23(5): 1331-1339. YU Yueqing, TIAN Hao. Error and compensation of parallel robot with joint clearances[J]. Optics and Precision Engineering, 2015, 23(5): 1331-1339.

[16] 趙剛練, 姜毅, 郝繼光, 等. 考慮圓柱鉸鏈間隙的多剛體系統動力學計算方法[J]. 振動與沖擊, 2013, 32(17): 171-176. ZHAO Ganglian, JING Yi, HAO Jiguang. Computational method of rigid mllltibody system dynamics considering cylindrical joint clearance[J]. Journal of Vibration and Shock, 2013, 32(17): 171-176.

[17] 王庚祥, 劉宏昭, 鄧培生. 考慮球面副間隙的并聯機構動力學模型[J]. 振動與沖擊, 2014, 33(10): 43-49. WANG Gengxiang, LIU Hongzhao, DENG Peisheng. Dynamic modeling for a parallel mechanism considering spherical joint clearance[J]. Journal of Vibration and Shock, 2014, 33(10): 43-49.

[18] 趙寬, 陳建軍, 曹鴻鈞, 等. 含間隙曲柄滑塊系統動力響應的隨機性分析[J]. 振動與沖擊, 2014, 33(11): 130-135. ZHAO Kuan, CHEN Jianjun, CAO Hongjun, et al.Randomness analysis of dynamic responses of a slider-crank system with clearances[J]. Journal of Vibration and Shock, 2014, 33(11): 130-135.

[19] OLYAEI A A, GHAZAVI M R. Stabilizing slider-crank mechanism with clearance joints[J]. Mechanism and Machine Theory, 2012, 53(3): 17-29.

[20] 王威, 沈政, 宋玉玲, 等. 含間隙和干摩擦的連桿機構系統動力學研究[J]. 振動與沖擊, 2015, 34(18): 210-214. WANG Wei, SHEN Zheng, SONG Yuling. System dynamics of linkage mechanism with clearance and dry friction[J]. Journal of Vibration and Shock, 2015, 34(18): 210-214.

[21] HOU Yulei, ZENG Daxing, ZHANG Zhanye, et al. A novel two degrees of freedom rotational decoupled parallel mechanism[J]. Applied Mechanics and Materials, 2012, 215/216: 293-296.

[22] LANKARANI H M, NIKRAVESH P E. Continuous contact force models for impact analysis in multibody systems[J]. Nonlinear Dynamics, 1994, 5(2): 193-207.

[23] FLORES P, AMBRSIO J, CLARO J C P, et al. Influence of the contact—Impact force model on the dynamic response of multi-body systems[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2006, 220(1): 21-34.

[25] FLORES P, AMBRSIO J. On the contact detection for contact-impact analysis in multibody systems[J]. Multibody System Dynamics, 2010, 24(5): 103-122.

Chaos andimpact phenomena of a RU-RPR decoupled parallel mechanism containing clearance

HOU Yulei1, WANG Yi1, JING Guoning1, ZENG Daxing1, QIU Xuesong1, LI Huijian2

(1. School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China;2. Key Laboratory of Mechanical Reliability for Heavy Equipments and Large Structures of Hebei Province, Yanshan University, Qinhuangdao 066004, China)

For chaos and impact phenomena in a mechanism with clearance, taking a two-rotation decoupled parallel mechanism RU-RPR (R stands for a revolute pair, U stands for a Hooke joint, P stands for a translation pair) proposed independently as a study object, considering clearance existing in a kinematic pair, combining with Lankarani-Nikravesh contact force model and Lagrange equation, the dynamic equation of the mechanism was established, and its chaos and impact phenomena were studied. Then the influences of different driving speeds and friction coefficients on chaos and impact phenomena were analyzed, and the relationship between the stability of the mechanism and impact phenomenon was investigated at the same time. The influences of an additional spring on dynamic characteristics of the mechanism were analyzed. The results showed that when changing drive speed or friction coefficient, the impact phenomenon still exists, while the motion of the mechanism can be changed from chaotic motion to periodic one, the stability of the mechanism is enhanced; there is no necessary relation between the stability of the mechanism and its impact phenomenon, and the impact level can be significantly weakened by adding springs.

parallel mechanism; clearance; dynamics; chaos; impact

國家自然科學基金(51205339;51305384)；中國博士后科學基金(2013M541199)

2015-08-16 修改稿收到日期：2015-12-30

侯雨雷 男，博士后，教授，博士生導師，1980年生

李慧劍 男，博士，教授，博士生導師，1980年生

TH113

A

10.13465/j.cnki.jvs.2017.01.032