基于GPS/北斗網絡RTK算法實現與結果分析

杜文選,嚴超,徐煒,王濤

(安徽理工大學 測繪學院,安徽 淮南 232001)

0 引 言

隨著衛星定位技術在各個領域的廣泛應用,其作業方式也在發生著巨大的變革,從單點定位擴展到廣域差分,從事后處理到實時定位與導航,其目的就是為了提高定位精度和應用范圍[1]。全球衛星導航系統(GNSS)精密實時動態(RTK)相對定位,通過對接收機間和星間做差消除衛星軌道誤差、大氣傳播延遲誤差以及衛星和接收機鐘差等誤差源,再利用高精度的載波相位觀測量,可以實現厘米級甚至毫米級精度的定位[2]。隨著互聯網的高速發展,區域和世界范圍內的信息和數據交流已變得相當容易,由此由多基站構成網絡的GNSS服務體系成為GNSS技術發展的最新趨勢。其中虛擬參考站(VRS)技術由于覆蓋范圍廣、定位精度高、可靠性高等優點成為目前最流行的一種網絡RTK技術[3]。

1 單基站RTK基本原理

單基站RTK由一個連續運行基準站,無線發射裝置、移動站三部分組成。連續運行基準站通過軟件實時向廣域網播發差分信息。移動站通過GPRS、CDMA網絡通訊方式與基準站服務器進行通訊,通過獲得的差分信息進行相對定位,獲取當前位置[4]。

GNSS接收機一般會獲取偽距觀測值與L1(B1)和L2(B2)載波相位觀測值;

偽距觀測值模型為

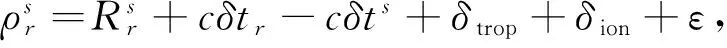
(1)

載波相位的觀測值模型為

Ns+ε，

聯系人: 杜文選 E-mail: 13685542895@163.com

載波相位雙差模型為

(3)

式中:A為基準站與B為移動站同時觀測參考衛星i及非參考衛星j. 可見,在測站和衛星的雙差觀測值中,接收機鐘差、衛星鐘差的影響已基本消除,對流層和電離層的影響得到進一步削弱[5]。

基準站A的天線相位中心坐標為(XA,YA,ZA)為已知值,設移動站B天線相位中心的近似坐標為(XB0,YB0,ZB0),其改正數為(δX2,δY2,δZ2),雙差觀測方程的線性化形式可寫為

[δXBδYBδZB]T-

(4)

lj=

ρAj-ρBi+ρAi).

(5)

基準站A和流動站B對同一組衛星進行觀測,衛星數為n,那么相應的誤差方程組為

V=AδX+l,

(6)

其中:

A=

(7)

(8)

δX=[δXBδYBδZB]T.

(9)

由最小二乘解算得出:

δX=-(ATPA)-1ATPL.

(10)

最后,由移動站近似坐標加改正坐標得出真值坐標。

2 多基站RTK定位原理

單基站RTK隨著基線距離的增加,對流層和電離層誤差的影響會變得越來越大,雙差改正的效果會越來越弱,使得定位精度大大降低。多基站RTK又稱網絡RTK技術,目前,VRS、FKP、MAC、CBI、ARS以及聯合單參考站差分解算技術是國內外主流的網絡RTK技術[7]。其中VRS技術是當前網絡RTK最常用的技術,能夠有效克服單基站RTK存在的缺陷,使用戶能夠在較大空間范圍內獲得均勻,高精度可靠的定位結果。

基于VRS的網絡RTK技術,各個固定參考站不直接向移動用戶發送任何改正信息,而是將所有的原始數據經過數據通訊鏈路發送至數據處理中心,移動站將其概略坐標(由偽距單點定位獲取)發送至控制中心,數據管理中心收到位置信息后會播發一組固定最佳的參考站,利用他們的數據在用戶位置附近模擬出一個虛擬參考站,與移動站形成超短基線[8]。將整體改正GPS軌道誤差、電離層、對流層以及大氣折射等誤差后的高精度差分信號發送給移動站,從而獲得高精度定位結果。

VRS的實現一般需要以下流程:

假定U表示流動站所在位置,V表示虛擬參考站VRS位置,A為主參考站所在位置,則主參考站A與虛擬參考站V之間的站間雙差觀測方程為[9]

(11)

由于A、V的坐標已知,主參考站A與虛擬參考站V間幾何距離雙差可直接計算,與分別為對流層與電離層誤差,可以通過基準站網對應誤差內插得到;VRS系統的關鍵是內插參考站處雙差綜合誤差和生成虛擬站觀測值[10]。

虛擬參考站V與流動站P之間的站間雙差觀測方程為

(12)

由于虛擬參考站與流動站之間的距離很短,兩測站與距離相關的雙差誤差殘差可以認為是相等的,即:

(13)

(14)

聯立方程(11)與方程(12)可得:

(15)

可根據相對定位模型進行定位。VRS技術實現流程如圖1所示。

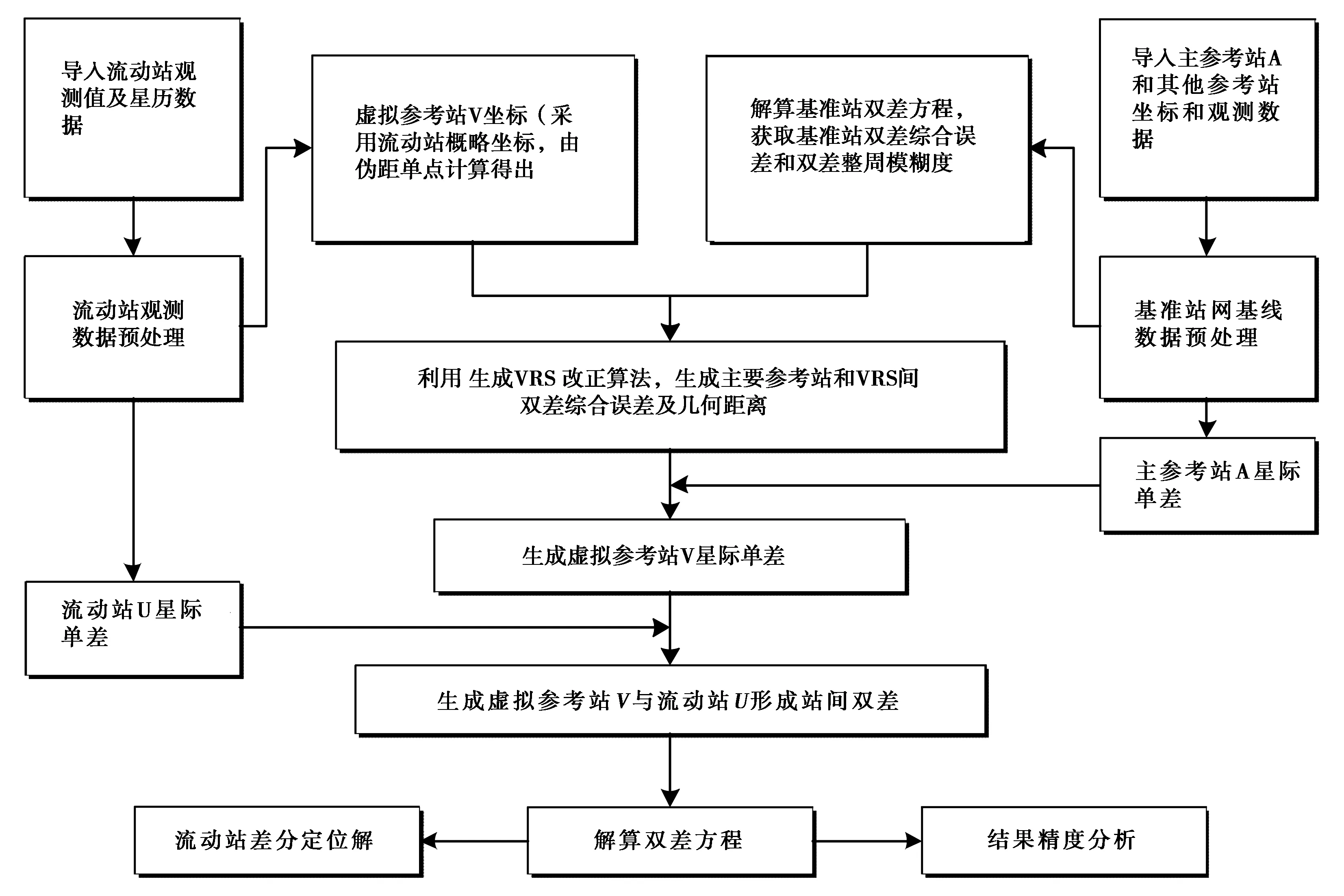
圖1 VRS技術實現流程圖

3 實驗分析

3.1 單基站定位實驗分析

實驗采用2017年06月06日06時至07時香港衛星定位參考基準網觀測數據已知基準點的觀測數據,以HKPC為基準站,選取的流動站HYC1,距離基準站3.966km.采用GPS/BDS雙系統雙頻觀測數據,時段長為30min,采樣間隔為1s,利用編寫的基于C++平臺的算法研究測試程序進行數據處理以及定位結果分析,將定位結果與靜態測量坐標比較得到WGS-84坐標系下HYC1點在X,Y,Z三個方向上的坐標差值,如圖2所示。

圖2 單基站RTK短基線定位三軸誤差及均方根值(RMS)

實驗得出基線長度為3.966 km的單基站RTK定位RMS可以達到厘米級定位,與靜態測量后處理定位坐標相比在X,Y,Z三個方向上的方向偏差可以達到厘米級。程序采用單歷元結算模糊度,由于觀測噪聲的原因，部分歷元發生跳躍。

另選取HYC1、HKLM、HKSC、HKOH、HKST與HKTK點為流動站,以HKPC為基準站,分別選取三次觀測數據進行計算,獲取三次計算平均坐標,得到計算結果與靜態測量坐標比較結果如表1所示。

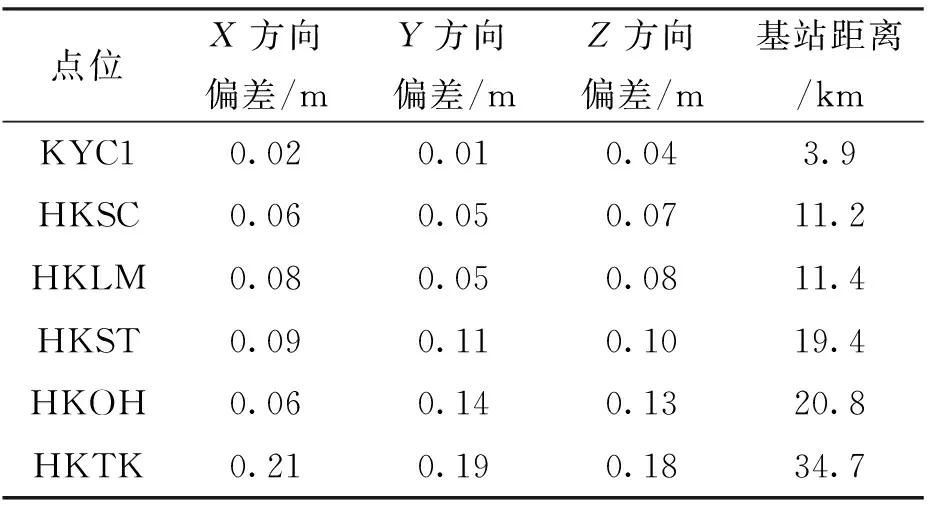
表1 測試點坐標測量統計表

由表1可知在測量基線較短(<15 km)情況下,單基站RTK測量結果與靜態測量結果比較,在WGS-84坐標系下三軸方向偏差能夠達到10 cm以內,但隨著基線的增加,在對流層和電離層等其他誤差的影響下測量誤差不斷增加,系統仍然可以進行RTK測量,但精度已經無法達到要求,只能進行分米級定位測量。

3.2 多基站定位實驗分析

本實驗采用2017年06月06日10時至11時香港衛星定位參考基準網觀測數據已知基準點的觀測數據,分別選取HKCL、HKTK、HKKS三個站點構成基準參考站網,選擇HKST站點為流動站,距離基準站30.5 km,采用GPS/BDS雙系統雙頻觀測數據,時段長為1 h,采樣間隔為1 s,進行數據處理及定位結果分析。

VRS基準站網參考站間首先采用雙頻線性組合法固定站間雙差寬巷模糊度,然后根據L1(B1)、L2(B2)的無電離層組合求出L1(B1)或L2(B2)的基頻雙差模糊度[11]。

參考站HKCL和參考站HKKS距離42.399 km,由圖3可以得出,兩基準站之間雙差寬巷模糊度由雙頻線性組合法得到C3號衛星與基準衛星間的雙差寬巷模糊度為-65周,而C3號衛星與基準星B1頻雙差模糊度采用無電離層組合法成功固定,雙差模糊度為7周,以此計算由大氣等因素產生的基準站間誤差,從而進一步計算虛擬觀測值的改正誤差。

采用雙差模型可以極大地消弱電離層和對流層誤差,但隨著基線長度的增加,雙差改正的效果會越來越弱,而選用VRS算法,通過基準站間的對流層和電離層誤差來內插出虛擬參考站與主參考站間的對流層和電離層誤差,通過改正可以消除或減弱虛擬參考站與主參考站間誤差,生成更加準確的虛擬觀測值。如圖4所示,分別為雙差對流層誤差殘差和雙差電離層誤差殘差,電離層抖動變化與當地時間有密切聯系。

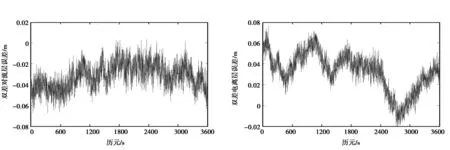
圖4 C3號衛星雙差對流層誤差和雙差電離層誤差

將定位結果與靜態測量坐標值比較,可以得到X、Y、Z三個方向的方向偏差如圖5所示。

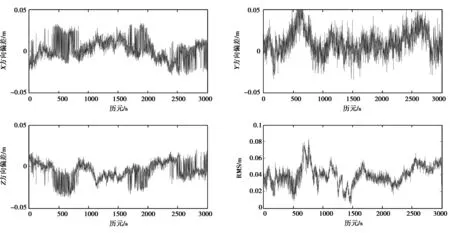
圖5 多基站RTK解算三軸方向偏差與RMS值

將基準站間的對流層和電離層誤差內插出虛擬參考站與主參考站間的綜合誤差,剔除粗差后生成的虛擬觀測值與流動站的觀測數據構成誤差觀測方程,通過實驗計算結果可以看出,當流動站與基準站相距30.5 km時RMS值可以達到厘米級,且多基站網絡RTK計算結果與靜態測量坐標偏差不超過10 cm,如圖5所示。當基線的長度超過一定距離時,單基線RTK由于雙差模型對電離層和對流層的改正效果變差,定位精度下降,如表1所示,而對于多基站RTK通過對電離層和對流層的改正,使定位精度得到了提升,可以達到厘米級定位精度。

4 結束語

本文通過使用實際觀測值數據計算單基站與多基站RTK的定位結果,分析得出當流動站與基準站構成較短基線時,直接進行相對定位可以得到厘米級定位結果,但隨著基線距離的增長,雙差模型對電離層和對流層的改正效果變弱,此時單基站網絡RTK會得到較差結果,而多基站網絡RTK利用VRS算法可以有效地改正誤差,即使流動站與參考站構成中長基線也會快速得到厘米級定位結果,在快速定位工作中極大地提高了工作效率,滿足工作的精度需求。

[1] 余學祥,王堅,劉紹堂,等.GPS測量與數據處理[M].北京：中國礦業大學出版社,2013.

[2] 寧津生,姚宜斌,張小紅.全球導航衛星系統發展綜述[J].導航定位學報,2013,1(1):3-8.

[3] 潘樹國,王慶,王慧青.基于VRS的GPS實時差分研究及測試[J].電子測量與儀器學報,2006,20(6):21-25.

[4] 鄭廷隆.單基準站RTK GPS實時定位基本原理及應用[J].吉林地質,2010,29(1):150-152.

[5] 謝建濤,郝金明,邱璇,等.GPS/VRS對流層延遲誤差內插模型研究[J].測繪與空間地理信息,2013,36(2):127-129.

[6] 魏瑞娟,李學軍,任維成,等.單基站CORS的建設與應用研究[J].測繪通報, 2010(6):23-26.

[7] 王靜,趙興旺,劉超,等.基于正則化的GPS/BDS單頻單歷元模糊度固定[J].大地測量與地球動力學,2016(12)：1083-1087.

[8] 唐文杰,呂志偉,王兵浩,等.基于北斗CORS的網絡RTK定位精度分析[C].//中國衛星導航學術年會,2015.

[9] 呂志偉.基于連續運行基準站的動態定位理論與方法研究[D].鄭州:解放軍信息工程大學,2010.

[10]李成鋼,羅小軍,王長委,等.基于Ntrip的Beidou/GPS雙模網絡RTK服務性能研究[C].//中國衛星導航學術年會,2014.

[11]祝會忠,徐愛功,高猛,等.BDS網絡RTK中距離參考站整周模糊度單歷元解算[J].測繪學報,2016,45(1):50-57.