GPS/BDS/GALILEO多系統融合偽距單點定位性能分析

賈雪,徐煒

(安徽理工大學 測繪學院,安徽 淮南 232001)

0 引 言

目前,我國的BDS系統已實現對亞太周邊地區的覆蓋,并按照“三步走”的發展戰略,計劃2020年完成35顆衛星發射組網,為全球用戶提供服務[1]。同時,歐盟的GALILEO系統也正處于建設階段,截止2017年8月可觀測衛星數約在14顆左右,已初步具備定位能力,伴隨著GPS現代化的實施,GPS單點定位的能力也逐步提高,定位精度達到1～5 m,在軌衛星共31顆[2]。

在單點定位時,定位精度受可見衛星數目的影響較大,在有建筑物或樹木的遮擋區域,單系統的可見衛星數目大大減少,導致單系統定位無法獲得可靠的定位結果,多系統的融合定位可以增加可見衛星的數量、改善衛星的空間幾何構型強度、提高定位的精度[3]。國內外學者對BDS、GPS多系統融合定位的研究較多,而對BDS、GPS、GALILEO三系統組合定位的研究卻較少。

鑒于此,本文在截止高度角10°、15°、20°、30°、40°的情況下,進行了GPS、BDS、GPS/BDS、GPS/GALILEO、BDS/GALILEO、GPS/BDS/GALILEO 6種模式偽距單點定位解算,并對其定位精度進行了比較。

1 GPS、BDS、GAILIEO單點定位模型

1.1 時間系統與坐標系統的統一

GPS采用GPS時(GPS time,GPST)和WGS-84坐標系(World Geodetic System 1984,WGS-84),BDS采用BDS時(BDS time,BDST)和CGCS 2000大地坐標系(China Geodetic Coordinate System 2000,CGCS2000),GALILEO采用GST時(Galileo System Time,GST)和GTRF坐標系(Galileo Terrestrial Reference Frame,GTRF),GPS、BDS、GALILEO的時間基準與坐標基礎都存在差異,因此在進行組合定位時需要將兩者的時間系統與坐標系統進行轉換和統一起來[4-6]。

聯系人: 賈雪 E-mail: 978256064@qq.com;

BDS與GPS系統均采用原子時,秒長的定義相同,也都采用周和周內秒數進行計數,不同在于GPST的起始時間為1980年1月6日的0時0分0秒的協調世界時(UTC),而BDST的起始時間是2006年1月1日0時0分0秒的UTC,GPS、BDS時間系統關系如圖1所示。

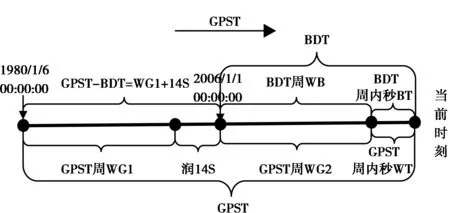
圖1 GPST與BDT轉換關系圖

GPST與BDST的轉換關系可以表示為

BDST周數=GPST周數+1356,

BDST周內秒數=GPST周內秒數+14.

但在GPST周內秒數+14大于604800時需要將BDST周數加1。

GALILEO采用的GST時間系統與國際原子鐘時間(TAI)同步,標準誤差為33 ns,GPST與GST的轉換公式為:

GPST=GST-19S±30 ns.

WGS-84坐標系與CGCS2000坐標系的所定義的大地原點、尺度、定向是相同的,參考橢球面參數也較為相近,唯有扁率有微小的差異。WGS-84坐標系經過優化后的精度可達到2 cm,與ITRF精度基本一致,而CGCS2000與ITRF的差異大約在5 cm,所以,WGS-84與CGCS2000存在cm級別的差異;而GTRF與WGS-84坐標系統的差異非常小,一般為1～2 cm,在進行非精密測量時可將三個坐標系間的差異忽略不計,不需要進行坐標系統間的轉換[7-8]。對于偽距單點定位而言,由于其定位精度在米級,因此無需進行坐標系統之間的轉換,直接將其視為統一坐標系統使用即可[9]。

1.2 單點定位模型

GPS、BDS、GALILEO偽距觀測方程可以統一表示為

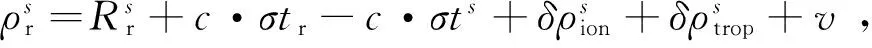
(1)式中: 設接收機的坐標為(XrYr,Zr);(Xs,Ys,Zs)

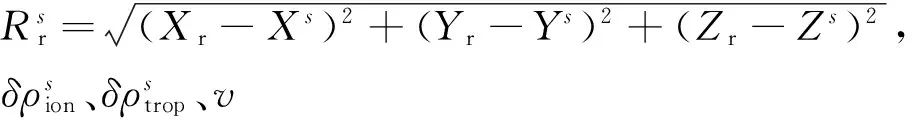
V=AδX-L，

(2)

式中:

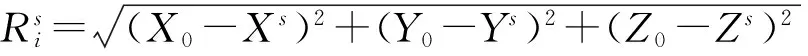
δX=(ATPA)-1ATPL.

(3)

單系統單點定位的未知參數有3個坐標分量和1個接收機鐘差,雙系統融合單點定位的未知參數有3個坐標分量和2個接收機鐘差,三系統融合單點定位的未知參數有3個坐標分量和3個接收機鐘差。因此,單系統單點定位時至少需要同時觀測到4顆衛星,雙系統組合單點定位時至少需要同時觀測到5顆衛星,三系統組合單點定位時至少需要同時觀測到6顆衛星[10]。在多系統融合計算時不同系統間視為等權,同系統間使用高度角定權,多系統融合偽距單點定位流程如圖2所示。

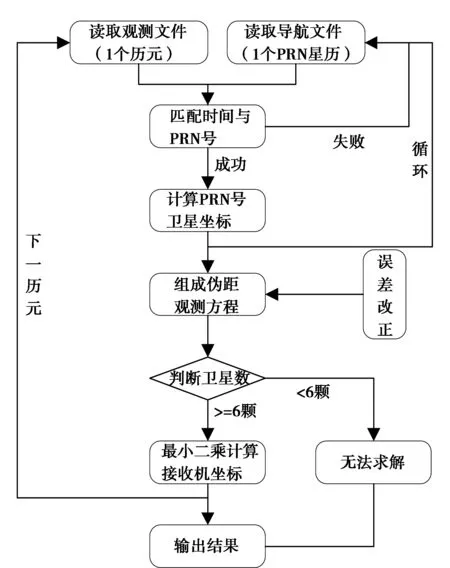
圖2 多系統融合偽距單點定位流程圖

1.3 主要誤差項的處理

在單點定位中,除了電離層延遲、對流層延遲、多路徑效應、接收機鐘差、衛星鐘差外,還有相對論效應、衛星軌道誤差、天線相位中心誤差、地球旋轉誤差等。本文對各個誤差項的改正為:對于電離層延遲,采用Klobuchar模型進行改正,對流層延遲采用Saastamoinen模型改正,衛星鐘差的改正模型為:δt=a0+a1(t-t0)+a2(t-t0)2,其中t為衛星鐘觀測時刻,t0為參考時刻,a0、a1、a2可以由

廣播星歷得到。相對論效應的改正模型為

由于地球自轉對衛星坐標進行的改正為

2 實驗數據處理與分析

2.1 GPS/BDS/GALILEO單點定位性能分析

本實驗采用香港連續運行參考站HKMW站點采集的數據,觀測時間為2017年8月12日0時0分0秒至2017年8月13日0時0分0秒,數據采樣間隔為30 s。

分別對GPS(G)、BDS(C)、BGS+GALILEO(CE)組合、GPS+GALILEO(GE)組合、GPS+BDS(GC)組合、GPS+BDS+GALILEO(GCE)組合進行偽距單點定位,由于GAILIEO系統在某些時刻的可見衛星數少于4顆,故不對GALILEO單系統進行單點定位分析。設置衛星截止高度角為10°,對比各種定位模式的可見衛星數,PDOP值,并將以ORS站網解算出的HKMW站點參考坐標與與計算結果進行求差,得出X、Y、Z三個坐標分量的偏差及RMS值。可見衛星數、PDOP值、X、Y、Z坐標偏差變化如圖3所示。

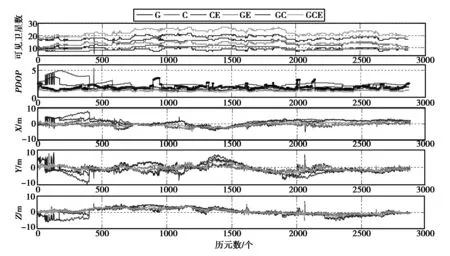
圖3 測站的可見衛星數、PDOP值及X、Y、Z方向的偏差

從圖3可以看出,BDS系統的穩定性比GPS系統的穩定性低,GPS/BDS/GALILEO組合系統的穩定性最好。BDS的PDOP值高于GPS,GPS的PDOP值高于BDS/GPS組合定位的PDOP值,這說明雖然BDS已經能夠實現對亞太地區的覆蓋,但還未實現對全球的組網,衛星的空間分布較GPS稍差,而GPS/BDS/GALILEO的組合定位使得位可見的衛星個數增加了2倍,大大增加了導航衛星的個數,提高了空間幾何構型的強度,使得定位的PDOP值得到了降低。而由于GALILEO正在處于建設階段,可觀測定位衛星數量較少,因此相對于BDS/GPS的組合,GPS/BDS/GALILEO的組合對定位精度的提升并不明顯。

利用這6種方法解算出的HKMW測站三維坐標分量的RMS值、全天平均PDOP值、平均可見衛星數量如表1所示。

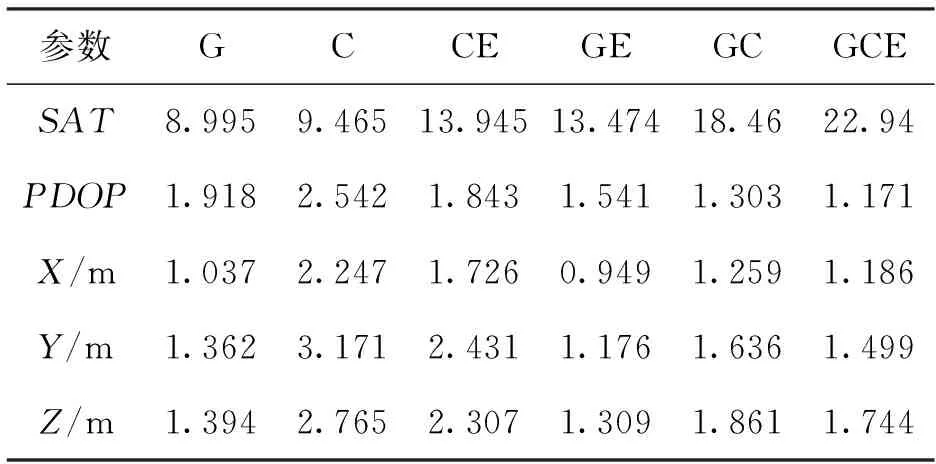
表1 站點平均可見衛星數、PDOP值及坐標分量的RMS值

從圖3及表1可得出,BDS的可見衛星數比GPS的可見衛星數較多,得益于BDS的GEO衛星與IGSO衛星的作用,但單BDS比單GPS的PDOP值、三維坐標的偏差卻要大。

GPS/BDS/GALILEO組合定位的可見衛星數相對于單GPS、BDS系統提升了255.03%、243.66%,PDOP值減小了38.94%、53.93%.其中,在X方向,BDS/GPS/GALILEO組合解算相對單GPS系統減小了13.1%,相對BDS系統提高了47.2%,這是由于組合定位雖然增加了可見衛星數,但由于BDS偽距的誤差相對較大,造成定位精度的減弱;在Y方向,BDS/GPS/GALILEO組合解算相對單GPS系統減小了10.0%,相對BDS系統提高了52.7%;在Z方向,BDS/GPS/GALILEO組合解算相對單GPS系統減小了25.1%,相對BDS系統提高了36.9%.

GPS/GALILEO組合定位的三維坐標偏差最小,相對BDS/GALILEO組合的坐標偏差分別減小了0.777 m、1.255 m、0.998 m,相對BDS/GALILEO組合的坐標偏差分別減小了0.237 m、0.323 m、0.435 m,其主要原因在于BDS GEO衛星軌道和鐘差精度偏低,從而導致了定位精度較差。

2.2 不同截止衛星高度角度單點定位性能分析

為了驗證多系統組合在不同高度角情況下的單點定位性能,分別設置截止衛星高度角為15°、20°、30°、40°,不同截止衛星高度角的可見衛星數、PDOP值變化如圖4～圖6所示。

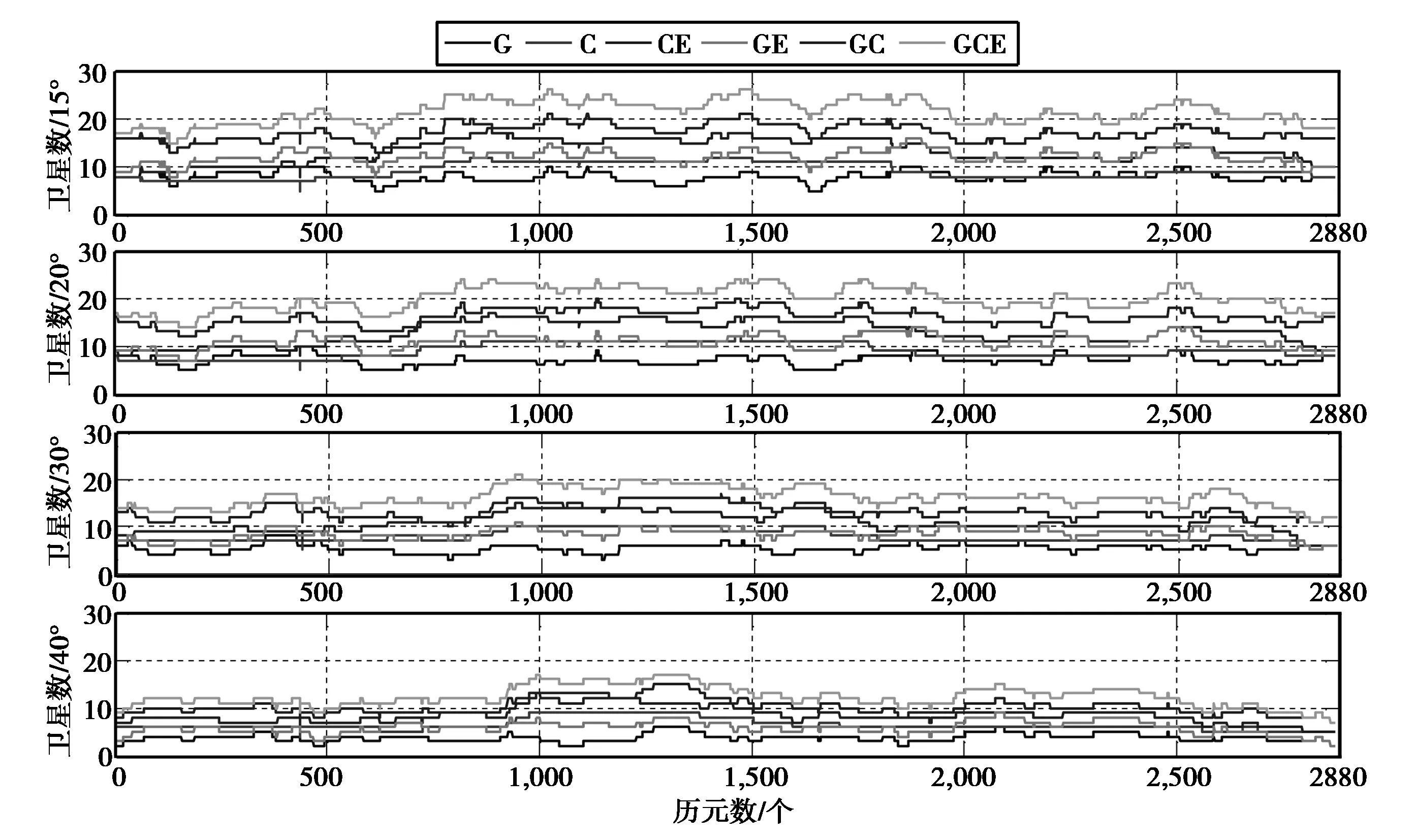
圖4 不同截止衛星高度角可見衛星數目變化

圖5 不同截止衛星高度角PDOP變化圖

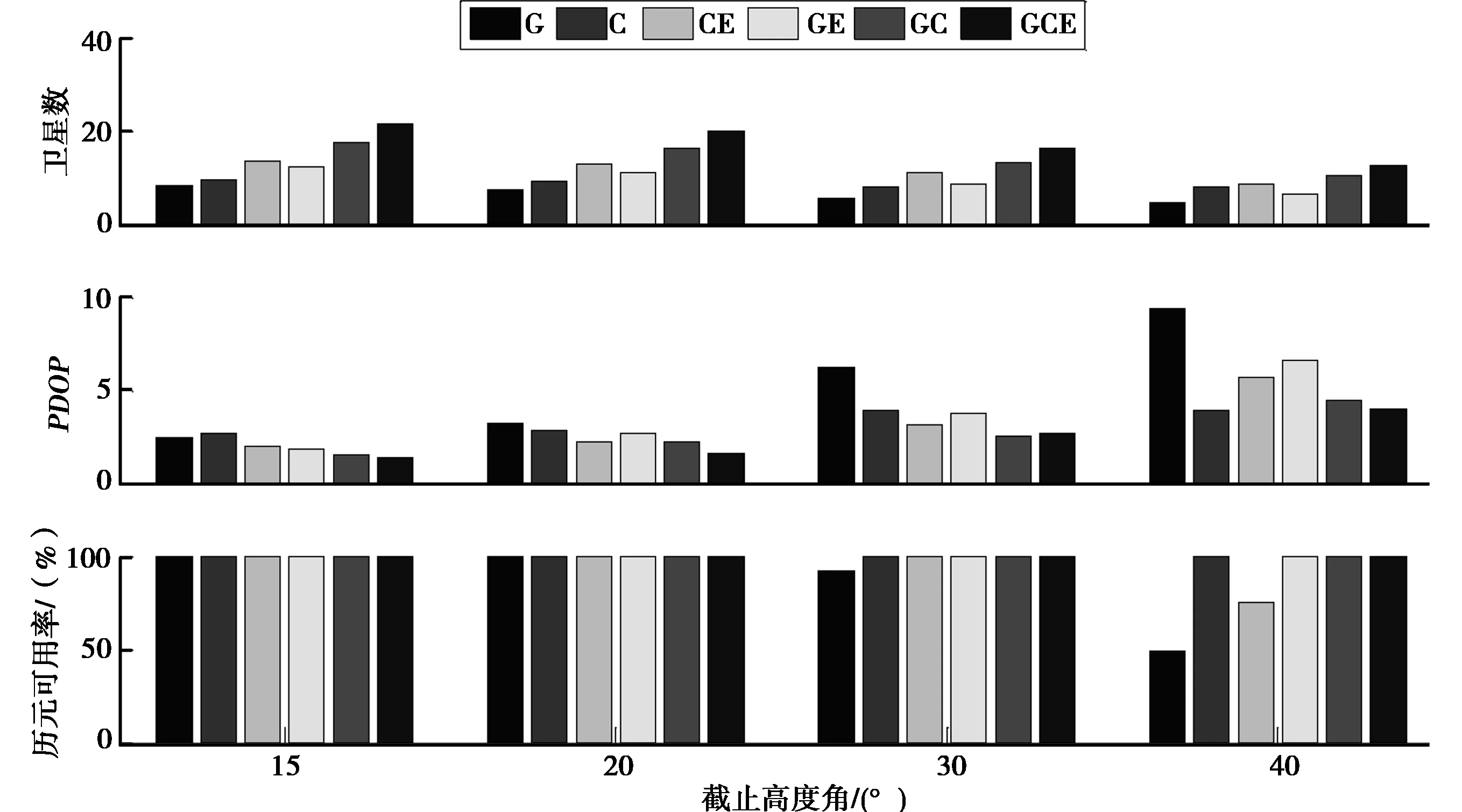
圖6 平均可見衛星數、PDOP值、歷元可用度隨高度角變化情況

由圖4、圖6可知,在截止衛星高度角為15°、20°、30°、40°的情況下,HKMW站GCE組合的平均可見衛星數分別為21.45、19.91、16.20、12.33顆,GGA組合的平均衛星數為12.183、10.985、8.36、6.45顆,BGA組合的平均可見衛星數為13.42、12.825、10.85、10.58顆,單GPS系統的可見衛星數為8.036、7.136、5.46、4.41顆,單BDS系統的可見衛星數為9.242、9.01、7.854、7.84顆,組合系統的可見衛星數始終遠遠多于單系統,其中GBGA組合在截止高度角為40°時的可見衛星數比單GPS、BDS系統在高度角為15°時的可見衛星數還多3～4顆。在截止高度角為30°時,GPS系統的可用歷元為92.066%,截止高度角為40°時,GPS系統的可用度為48.816%,而BDS系統由于GEO與IGSO的作用,歷元的可用度一直為100%,對于CE、GE、GC、GCE各組合系統而言,仍然可以完全實現定位。

由圖4、圖6可知,在截止高度角15°、20°、30°、40°的情況下,GPS單系統的PDOP值分別為2.41、3.17、6.22、9.37,BDS單系統的PDOP值為2.67、2.79、3.88、6.61,BGA組合的PDOP值為1.98、2.17、3.09、5.63,GGA組合的PDOP值為1.82、2.67、3.75、6.61,GBGA組合的PDOP值為1.34、1.54、2.62、3.96,對于各組合系統、GPS單系統、BDS單系統,PDOP值與衛星截止高度角成正比,同一觀測時段BDS的PDOP值均比GPS高,因此,雖然BDS的可見衛星數目大于GPS系統,但是衛星的空間幾何構型強度比GPS系統差;在衛星高度角為40°時,GCE組合在HKMW站的PDOP值變化較為平穩,基本維持在4.0左右,說明組合系統偽距單點定位的幾何圖形得到了增強,定位精度得到了提高。

全天全觀測時段內,在15°、20°、30°、40°截止衛星高度角下GPS、BDS、BDS/GALILEO、GPS/GALILEO、GPS/BDS/GALILEOX、Y、Z方向的定位偏差位如圖7所示。

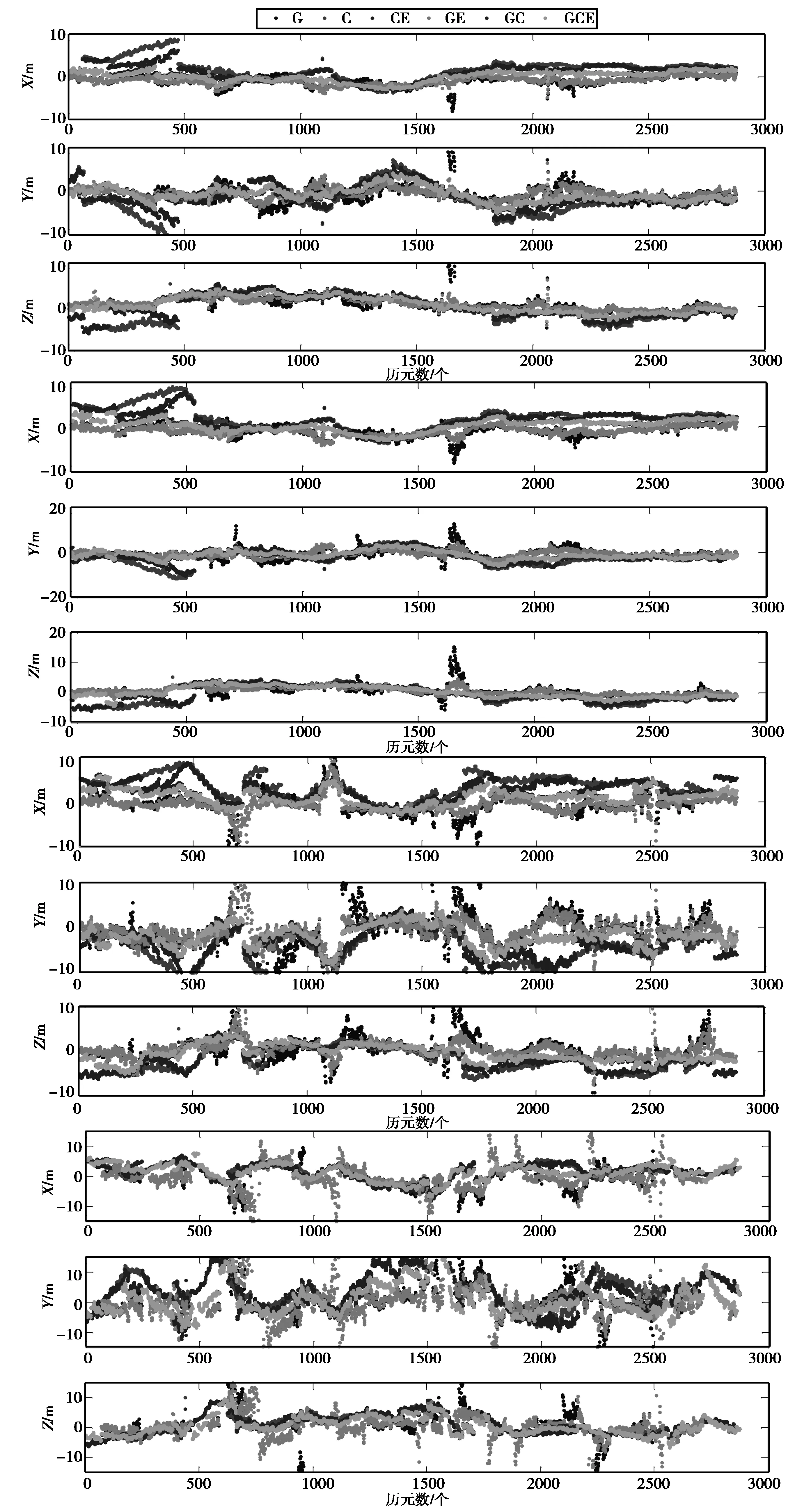
圖7 從上到下15°、20°、30°、40°時衛星高度角三維坐標偏差

由圖7可知,在不同截止衛星高度角情況下,GCE組合定位的穩定性都最高,在截止高度角為15°、20°時,由于GPS衛星的可見衛星受到的影響較小,而BDS 因其GEO衛星軌道和鐘差精度偏低,故GPS單系統的定位精度優于BDS單系統,GE組合的定位精度最高,其RMS值與單GPS系統和GCE組合定位的RMS值基本相當。當截止衛星高度角為30°時,GPS單系統的歷元可用度為90%,此時GPS與BDS系統的定位精度相當,而當截止衛星高度角為40°時,GPS單系統的歷元可用度為48.816%,可見衛星數目下降,GPS系統在X、Y、Z方向的RMS值比BDS系統的都要大,GE組合定位的RMS值也隨之下降,此時GCE組合仍能實現定位,說明了組合定位的優勢。

3 結束語

隨著我國BDS系統面向全球的組網、以及GALILIEO系統的建設,本文通過香港HKMW全天的實測數據,對GPS、BDS、BGS/GALILEO、GPS/GALILEO、GPS/BDS/GALILEO在不同截止衛星高度角下的定位結果進行了分析,得出以下幾點結論:

1) BDS單點定位的精度已經能達到米級,但BDS系統的定位精度仍稍遜于GPS系統,GPS/BDS/GALIEO組合系統的穩定性最好,在X、Y、Z方向的定位精度都優于單系統。

2) GPS/BDS/GALILEO組合系統比單系統單點定位可以觀測到更多的可見衛星,提高了系統的可靠性與穩定性。GBGA組合系統的GDOP值遠小于單系統的PDOP值,取決于可見衛星數的增加,使得衛星的空間幾何構型得到了增強。

3) GPS/BDS/GALILEO組合定位在衛星截止高度角增加的時候,定位優勢較為明顯,定位精度和穩定性都優于單系統。其中,當截止高度角在15°、20°時,GBGA的定位精度比單GPS系統的定位稍差,但在截止高度角達到30°、40°時,由于GPS可見衛星數的減少,GPS系統的歷元可用度分別為92%、48%,此時GBGA組合系統在X、Y、Z方向的定位結果都較單系統平穩,定位精度優于單系統。

[1] 楊元喜.北斗衛星導航系統的發展、貢獻與挑戰[J].測繪學報,2010,39(1):1-5.

[2] 李博,徐愛功,祝會忠,等.不同截止高度角BDS/GPS偽距單點定位性能分析[J].測繪科學,2016,41(12):32-38.

[3] 羅小敏,蔡昌盛.GPS/GALILEO組合單點定位精度分析[J].大地測量與地球動力學,2013,33(3):137-140.

[4] 魏二虎,劉學習,劉經南.北斗+GPS組合單點定位精度評價與分析[J].測繪通報,2017(5):1-5.

[5] 李林紅,何繡鳳,張化凝.COMPASS偽距單點定位精度分析[J].大地測量與地球動力學,2013,33(2):58-62.

[6] 鄒波,李小莉,陶庭葉.GPS/BDS組合系統偽距單點定位模型精度分析[J].測繪科學,2014,39(10):30-32+59.

[7] 袁宏超,秘金鐘,高猛,等.雙導航定位系統偽距單點定位方法與精度分析[J].導航定位學報,2014,2(3):38-43.

[8] 任曉東,張柯柯,李星星,等.BeiDou、Galileo、GLONASS、GPS多系統融合精度單點[J].測繪學報,2015,44(12):1307-1313.

[9] 安向東.GPS與北斗偽距單點定位性能對比分析[J].全球定位系統,2014,38(3):8-14.

[10] 嚴超,余學祥,徐煒,等.GPS/BDS/GLONASS組合偽距單點定位性能測試與分析[J].全球定位系統,2017,42(2):25-31.