分數階PID控制對單自由度線性振子的影響

牛江川， 申永軍， 楊紹普， 李素娟

(石家莊鐵道大學 機械工程學院，石家莊 050043)

分數階PID控制對單自由度線性振子的影響

牛江川， 申永軍， 楊紹普， 李素娟

(石家莊鐵道大學 機械工程學院，石家莊 050043)

研究了基于速度反饋分數階PID控制的單自由度線性振子的自由振動，利用平均法得到了系統的近似解析解。研究發現分數階PID控制的比例環節以等效線性阻尼的形式影響系統的振幅，積分環節以等效線性阻尼和等效線性剛度的形式影響系統的動力學特性，微分環節以等效線性阻尼和等效線性負剛度的形式影響系統的動力學特性。對近似解析解和數值解進行了比較，二者吻合良好，驗證了求解過程和近似解析解的正確性。通過系統響應的性能指標分析了分數階PID控制的比例系數、積分環節系數、微分環節系數以及分數階階次變化時，對系統控制性能的影響。最后，通過單自由度1/4車輛懸架模型的控制實例，說明了分數階PID的參數整定過程。

分數階PID控制；平均法；近似解析解

分數階微積分理論在近年來取得了較大的研究進展[1-5]。由于很多工程問題可以用分數階微分或積分方程來描述，因此分數階微積分在工程中的應用越來越廣泛。其中一個很重要的方面就是在控制系統中引入分數階反饋項，利用分數階反饋的魯棒性好、抗噪聲能力強等優點，提高系統的控制效果。例如，CHEN等[6]研究了分數階阻尼對van der Pol系統動力學特性的影響；張成芬等[7]研究了分數階Liu系統的混沌動力學行為；吳光強等[8]利用分數階微積分的天棚阻尼控制策略抑制汽車車身共振；孫會來等[9]在油氣懸架運動微分方程基礎上建立了分數階Bagley-Torvik方程。

PODLUBNY[10]在研究分數階控制系統的基礎上提出了分數階PID控制器,與傳統整數階PID相比，分數階PID控制在穩定性和動態性能方面具有很大優勢。目前學者們對分數階PID控制的研究[11-20]，主要集中在控制器的設計方法和控制器的穩定性分析以及最優控制等方面。直接通過系統時域響應來分析分數階PID參數對控制效果影響的成果尚不多見。本文以一個基于速度反饋的分數階PID控制的單自由度線性振子為例，利用平均法得到了系統自由振動的近似解析解，該近似解析解能以簡單的形式說明系統響應特性與分數階PID參數之間的對應關系。然后通過數值解驗證了近似解析解的正確性，并分析了分數階PID控制器的系數Kp、Ki、Kd以及分數階階次λ和δ變化時，對系統控制性能的影響。最后，通過一個控制實例說明了分數階PID的參數整定過程。

1 近似解析解

分數階PID控制器的時域數學模型為[10]

(1)

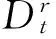
(2)

式中r為微分積分的階次，此處r為實數，分數階積分算子以0為積分下限，以t為積分上限。

單自由度線性振子由質量塊、彈簧以及阻尼組成。研究基于速度反饋分數階PID控制的單自由度線性振子的振動。設系統受到的擾動力為F，其系統結構如圖1所示。

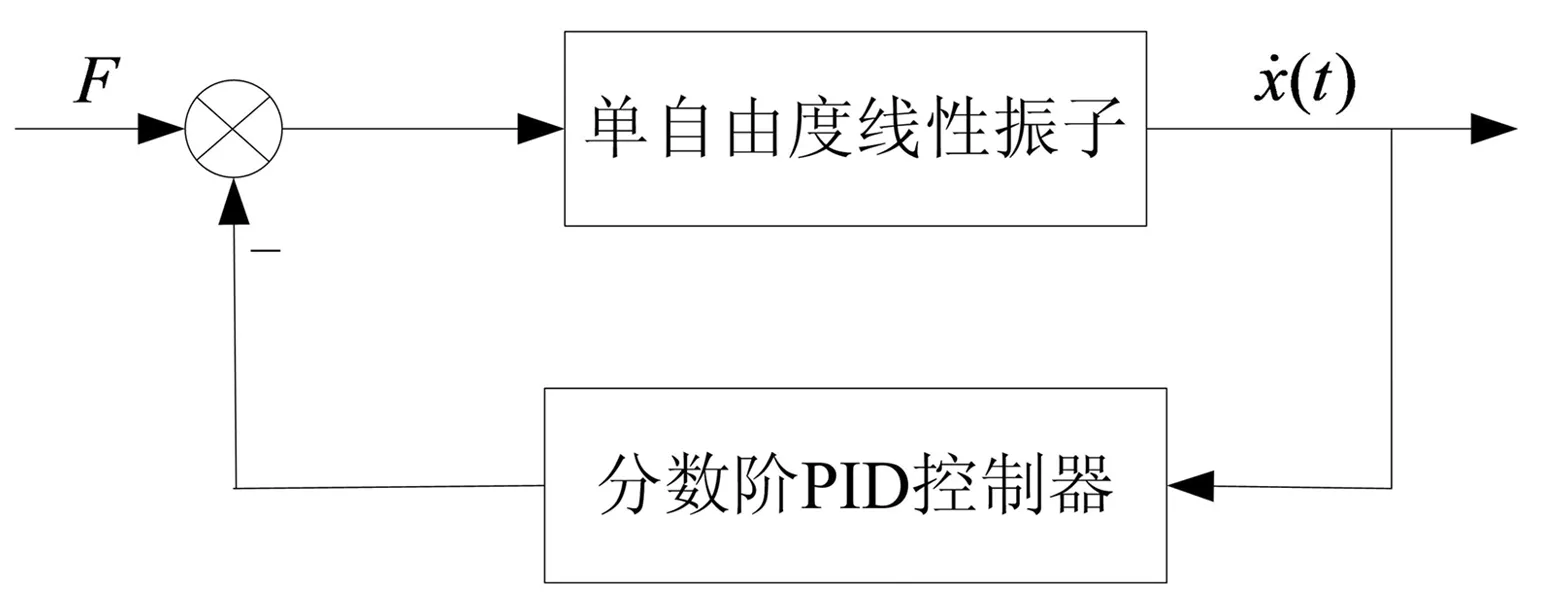
圖1 基于速度反饋的分數階PID控制系統Fig.1 Control system with fractional-order PID controller of velocity feedback

以系統自由振動的平衡位置為原點，以系統的輸出速度作為反饋量，考慮系統的自由振動問題，則系統受到的擾動力F=0，建立含有分數階PID控制的單自由度線性振子的運動方程，如式(3)所示。

(3)

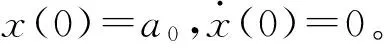
(4)

(5)

式中Γ(z)為Gamma函數，滿足Γ(z+1)=zΓ(z)。

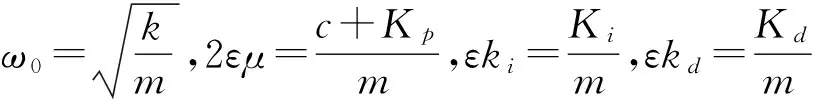
(6)

式(6)從形式上滿足了平均法求解的要求。利用平均法[21]求系統的一次近似解。設式(6)的解滿足

(7)

式中φ=ω0t+θ，則根據平均法可以得到

P2[a(t),θ]+P3[a(t),θ]}sinφ

(8a)

P2[a(t),θ]+P3[a(t),θ]}cosφ

(8b)

式中，P1[a(t),θ]=2μω0a(t)sinφ，

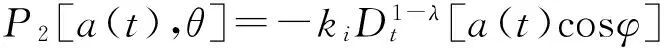
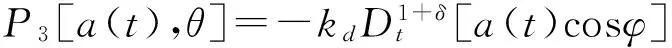
振幅a和相位θ是隨時間變化的ε的同階小量，與φ相比，它們變化緩慢。利用平均法，可以將式(8)在區間[0,T]之間進行積分平均，得到振幅a和相位θ的近似值。將式(8)改寫為

(9a)

(9b)

式中，如果Pi[a(t),θ](i=1,2,3)為周期函數，那么積分終止時間T可以取為T=2π;如果Pi[a(t),θ](i=1,2,3)為非周期函數，那么積分終止時間T可以取為T=∞。因此，式(9)中的第一部分積分為

(10a)

(10b)

為了計算式(9)中的其它部分，引入兩個基本公式

(11a)

(11b)

這兩個公式的求解過程可參見文獻[22-23]。

研究式(9a)的第二部分，并將式(5)代入，可以得到

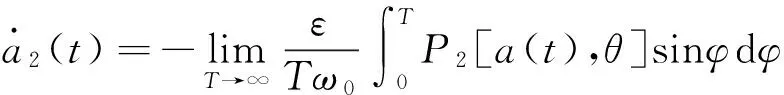
(12)

引入s=t-τ和ds=-dτ，則有

(13)

其中，

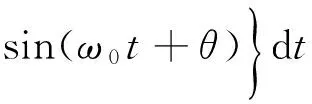
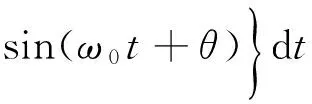
對式(13)中第一部分A1進行分部積分可以得到

(14)

當T→∞時發現式(14)的第二部分趨近于零，根據式(11)可以得到

(15)

同理，式(13)的第二部分A2也趨近于零，因此

(16a)

利用同樣的方法可以得到

(16b)

對于式(9)的第三部分，利用同樣的方法可以得到

(17a)

(17b)

將式(10)、(16)、(17)聯合起來，則有

(18a)

(18b)

解出振幅和相位，則有

(19a)

(19b)

將原系統參數代入式(19)，則得到

(20a)

(20b)

其中，五個新的參數為

C(P)=Kp

(21a)

(21b)

(21c)

(21d)

(21e)

系統的近似解析解可以表示為

其中，C=c+C(P)+C(I)+C(D)。這樣就得到了系統的近似解析解。式(22)表明，在系統(3)中，分數階PID通過參數C(P)、C(I)、C(D)增大了系統的阻尼，可以將參數C(P)、C(I)、C(D)分別定義為分數階PID比例環節、積分環節、微分環節引起的等效線性阻尼，并將參數C定義為系統的等效阻尼系數；通過參數K(I)增大了系統的剛度，可以將參數K(I)定義為積分環節引起的等效線性剛度；通過參數K(D)減小了系統的剛度，可以將參數K(D)定義為微分環節引起的等效線性負剛度。并令K=k+K(I)+K(D)，則可以將參數K定義為系統的等效線性剛度。

(23)

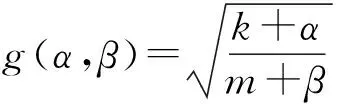
(24)

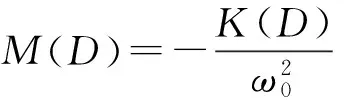
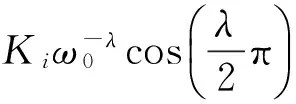
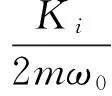
2 近似解析解和數值解的比較

研究系統(3)，選取某單自由度1/4車輛懸架模型參數：質量m=240 kg，彈簧剛度k=16 000 N/m，阻尼系數c=1 000 N·s/m，其它參數定義為Kp=1，Ki=1，Kd=1，λ=0.6，δ=0.4，a0=-1 m，根據式(22)可以繪制出系統振動位移的時間歷程，如圖2中實線所示，圖中橫軸為時間，縱軸為位移。為了進行比較，本文采用冪級數法計算系統(3)，其計算公式為[1,24]：

(25)

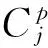
(26)

根據式(25)和式(26)，系統(3)可以表示為

(27a)

y(tn)=[-kx(tn)-(c+Kp)y(tn-1)-Kiz1(tn-1)-

(27b)

(27c)

z2(tn)=[-kx(tn)-(c+Kp)y(tn)-Kiz1(tn)-

(27d)

根據式(27)計算系統(3)的數值解，計算過程中時間步長h=0.001，分數階項的初值設定如下[25]：

(28a)

(28b)

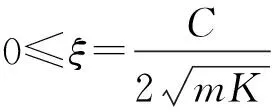
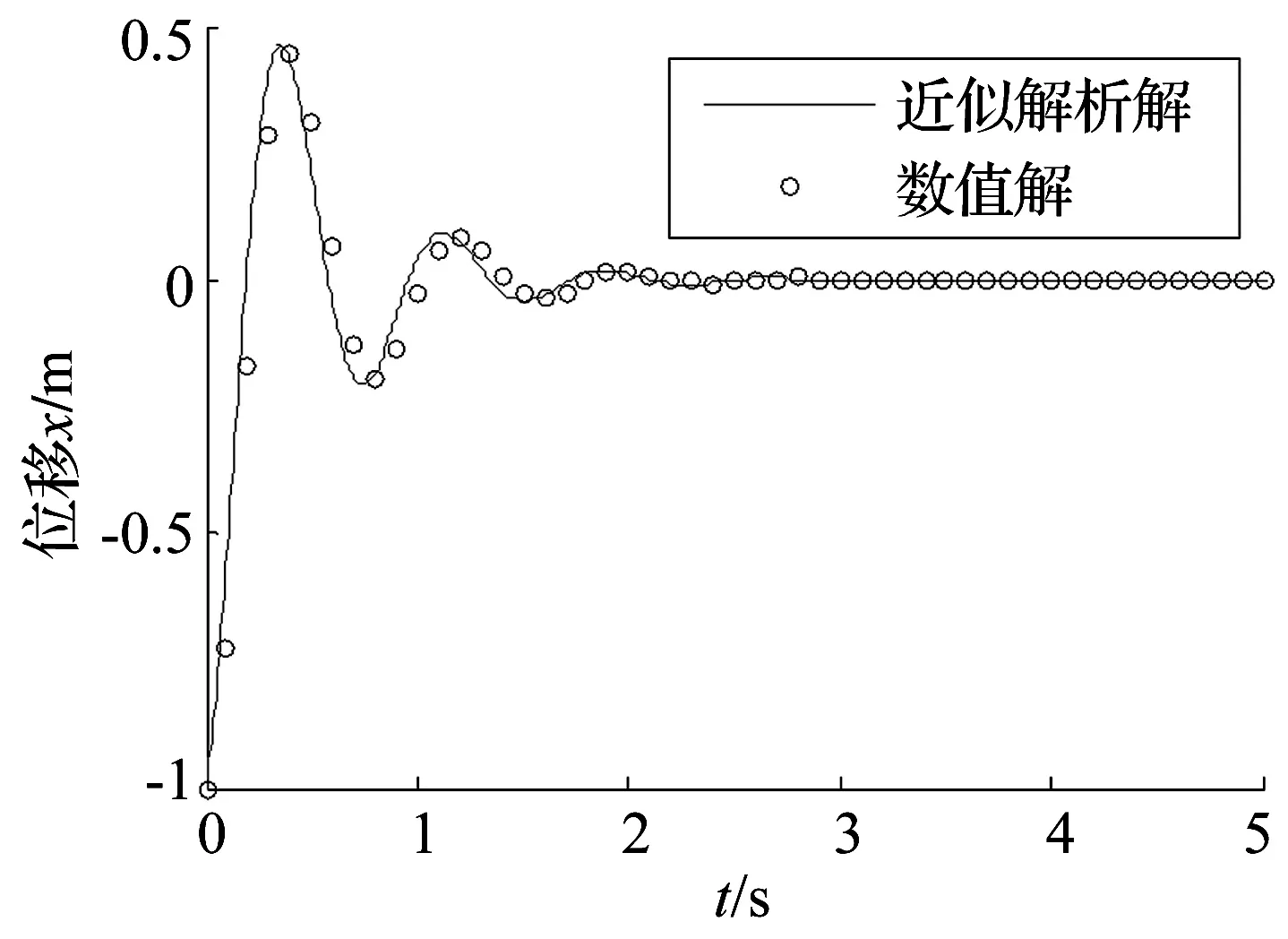
圖2 數值解和近似解析解比較Fig.2 Comparison of numerical solution and approximate analytical solution

3 分數階PID控制性能分析

下面分析分數階PID控制的系數Kp、Ki、Kd以及分數階階次λ和δ變化時，對系統控制性能的影響。參照二階振蕩系統的性能指標，分析分數階PID控制參數對系統的上升時間和峰值的影響。

(1)上升時間

系統響應曲線第一次達到穩態時，定義為上升時間tr。由式(22)得

(29)

求解方程，并利用式(23)進行化簡，上升時間為tr為：

(30)

由式(30)可知，當系統為欠阻尼系統時，上升時間與比例環節的等效線性剛度以及積分環節的等效線性負剛度有關。由式(21)可知，增大比例環節系數Kp，將增大系統的阻尼，當系統成為過阻尼系統時，上升時間將會增大。增大積分環節系數Ki，其階次λ保持不變時，將增大K(I)和系統的等效線性剛度K，使上升時間減少，加快系統的響應速度。增大微分環節系數Kd，其階次δ保持不變時，將減小K(D)和系統的等效線性剛度K，使上升時間增長，減慢系統的響應速度。

積分環節的分數階階次λ和系數Ki共同調節積分環節的作用。當積分環節分數階階次λ從0到1變化時，繪制出系統(3)的等效線性剛度曲線，如圖3所示。由圖3可見，隨著λ的增大，將使系統的等效線性剛度K先變大然后變小，在λ=0.4附近時系統的等效線性剛度最大，上升時間最短。

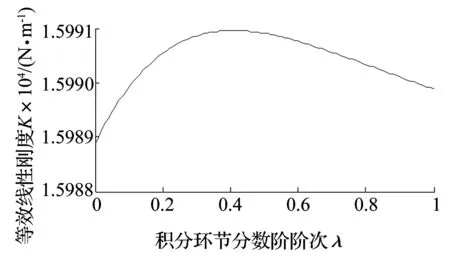
圖3 λ變化時的等效剛度曲線Fig.3 Equivalent linear stiffness with λ

微分環節的分數階階次δ和系數Kd共同調節微分環節的作用。當微分環節分數階階次δ從0到1變化時，繪制出系統(3)的等效線性剛度曲線，如圖4所示。由圖4可見，隨著δ的增大，將使系統的等效線性剛度K先略有增大再逐漸變小；上升時間也將先略有減少，再逐漸變長。

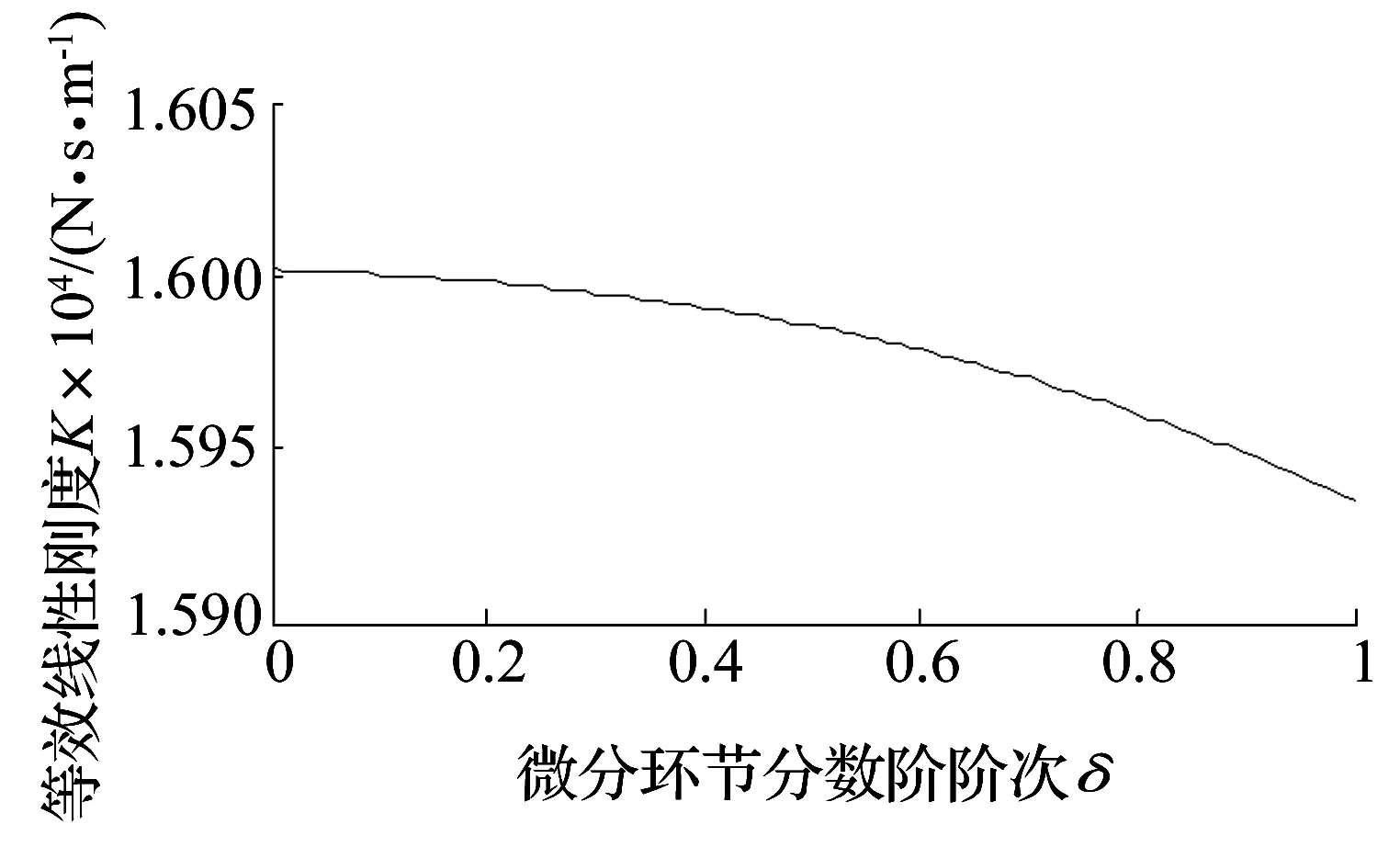
圖4 δ變化時的等效剛度曲線Fig.4 Equivalent linear stiffness with δ

(2)峰值時間及峰值

系統響應曲線達到第一個峰值時，定義為峰值時間tp。將式(22)對時間求導數，并令其為零，即由

(31)

整理后得到

(32)

因此，解得：

(33)

當t=tp時，代入式(22)，則可以計算出第一個峰值Mp，即

(34)

由式(21)和式(34)可知，隨著比例環節系數Kp的增大，等效阻尼比ξ逐漸增大，則第一個峰值將逐漸減小。當積分環節的系數Ki及其分數階階次λ、微分環節的系數Kd及其分數階階次δ分別變化時，繪制出系統(3)的等效阻尼比曲線，如圖5所示。

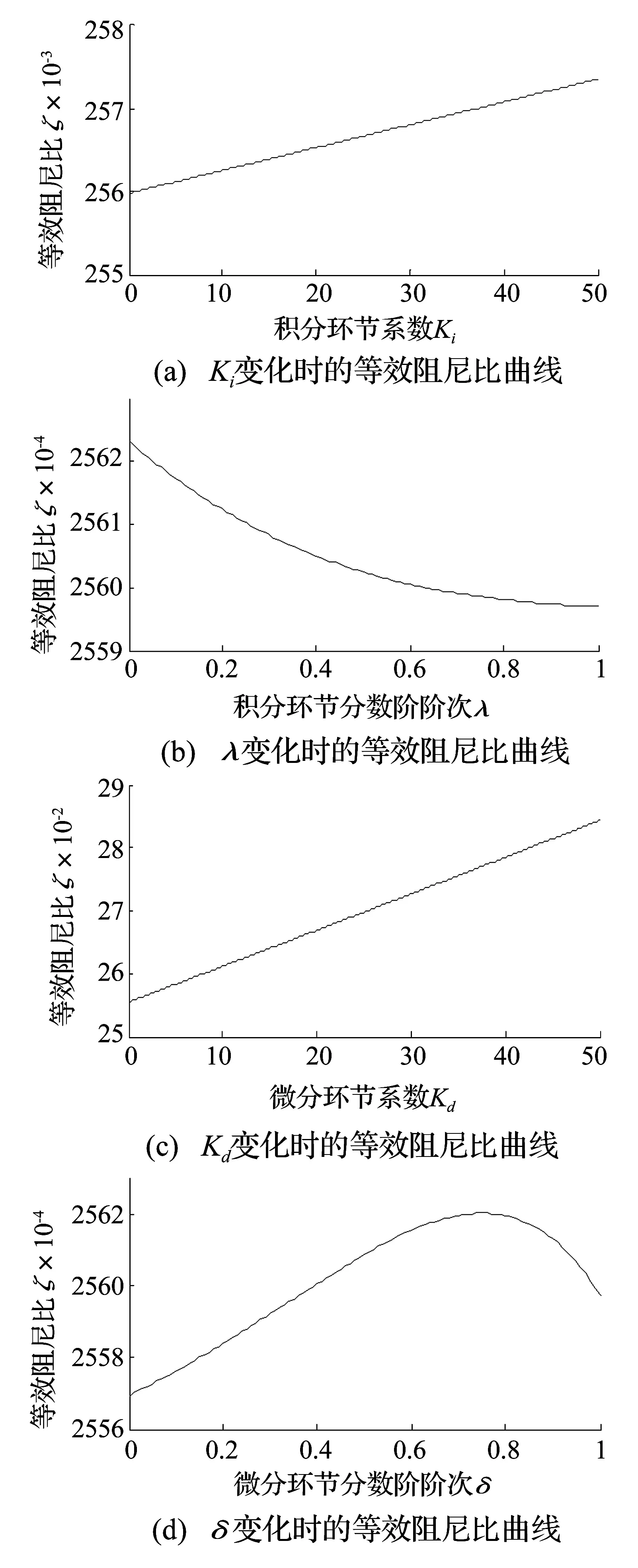
圖5 等效阻尼比曲線Fig.5 Equivalent damping ratio curves

由圖5(a)可知，隨著積分環節系數Ki的增大，等效阻尼比ξ逐漸增大，則第一個峰值將逐漸減小。由圖5(b)可知，隨著積分環節分數階階次λ的增大，等效阻尼比ξ逐漸減小，則第一個峰值逐漸增大。由圖5(c)可知，隨著微分環節系數Kd的增大，等效阻尼比ξ逐漸增大，則第一個峰值將逐漸減小。由圖5(d)可知，隨著微分環節分數階階次δ的增大，等效阻尼比ξ先逐漸增大然后減小，則第一個峰值將先逐漸減小后增大。

4 分數階PID控制實例

設計分數階PID控制器時，需要根據控制目標合理地選擇控制器參數，以提高系統的控制效果。下面以一個實例來說明分數階PID控制參數的整定過程和控制效果。

對于二階系統，一般希望系統工作在ξ=0.4～0.8的欠阻尼狀態，因為這個工作狀態的振蕩特性適度而且過渡過程較短。設單自由度1/4車輛懸架模型以ξ=0.4為設計目標對控制器參數進行整定，并保持系統的響應時間基本不變，以滿足一定的響應快速性和乘客的舒適度。根據前面的分析，僅包含比例環節就可以實現設計目標，但是若考慮車輛的載重量變化時懸架的靜撓度保持不變，控制器應包含比例、積分以及微分三個環節。

根據控制目標可以建立如下方程：

(35a)

(35b)

以分數階PID控制器的控制參數為變量，式(35)有無窮多解。為了便于計算，可以取λ=0.5和δ=0.5，并令比例環節引起的等效阻尼為調節阻尼的1/3，則可以得到一組解：Kp=189，Ki=768，Kd=94。根據式(22)繪制出PID控制參數整定前后系統振動位移的時間歷程，如圖6所示。從圖6中可以看出最大振幅得到了抑制，上升時間保持不變，達到了控制目標。

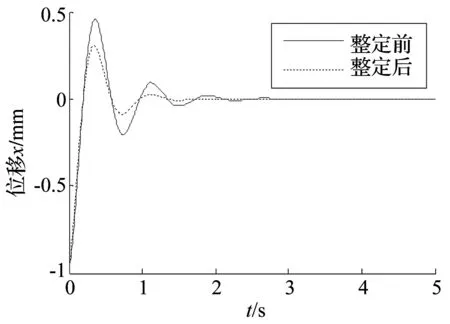
圖6 分數階PID參數整定前后比較Fig.6 Comparison of before and after parameters tuning

當λ=1和δ=1時，分數階PID轉換為傳統整數階PID。若采用整數階PID控制實現上述控制目標，整數階PID僅包含比例環節，也可以實現相同的控制效果。但是當車輛的載重量增加時，如果需要保持懸架的靜撓度固定不變，整數階PID需要增加積分環節以增大系統的剛度，同時為了滿足上升時間保持不變,同樣也需要包含微分環節。當傳統整數階PID各個環節的系數取整定后的分數階PID的參數時，根據式(22)繪制出分數階PID控制和傳統整數階PID控制的系統振動位移的時間歷程，如圖7所示。從圖7中可以看出，采用分數階PID控制的最大振幅比整數階PID的小，而且整數階PID控制的上升時間增大了，可見基于速度反饋的分數階PID控制對單自由度1/4車輛懸架模型的控制效果要優于傳統整數階PID控制。

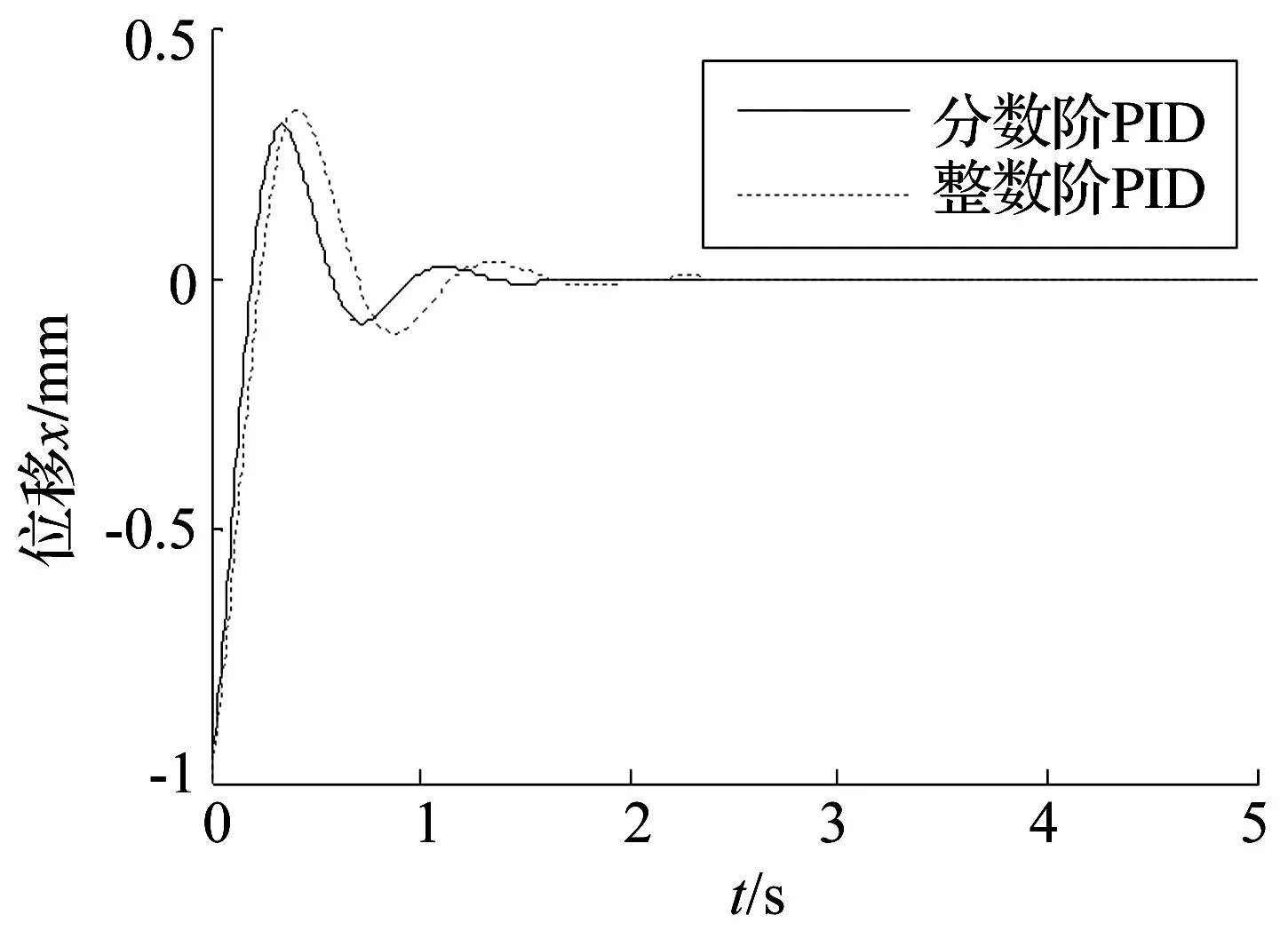
圖7 分數階PID與整數階PID控制效果比較Fig.7 Comparison between the control effects of fractional-order PID with integer-order PID

4 結 論

本文研究了基于速度反饋的分數階PID控制的單自由度線性振子的動力學特性，利用平均法求得了系統的近似解析解，并利用數值解驗證了方法和結果的正確性。定義了三個等效線性阻尼參數、一個等效線性剛度參數和一個等效線性負剛度參數，從理論上分析了分數階PID控制對系統動力學的影響。通過系統響應的性能指標，分析了分數階PID控制的系數Kp、Ki、Kd以及分數階階次λ和δ變化時，對系統控制性能的影響。最后，通過單自由度1/4車輛懸架模型的控制實例，證實了當控制參數相同時,基于速度反饋的分數階PID控制比傳統整數階PID控制具有明顯的優越性。

[1] PETRAS I. Fractional-order nonlinear systems[M]. Beijing: Higher Education Press, 2011.

[2] PODLUBNY I. Fractional differential equations [M]. New York: Academic Press, 1999.

[3] SHEN Y J, YANG S P, XING H J, et al. Primary resonance of duffing oscillator with fractional-order derivative [J]. Communication in Nonlinear Science and Numerical Simulation,2012,17(7): 3092-3100.

[4] ROSSIKHIN Y A, SHITIKOVA M V. Application of fractional derivatives to the analysis of damped vibrations of viscoelastic single mass systems[J]. Acta Mechanica,1997,120(1/2/3/4): 109-125.

[5] YANG S P, SHEN Y J. Recent advances in dynamics and control of hysteretic nonlinear systems[J].Chaos Solitons and Fractals, 2009,40(4): 1808-1822.

[6] CHEN J H, CHEN W C. Chaotic dynamics of the fractionally damped van der Pol equation[J].Chaos, Solitons and Fractals, 2008,35(1):188-198.

[7] 張成芬，高金峰，徐磊. 分數階Liu系統與分數階統一系統中的混沌現象及二者的異結構同步[J].物理學報,2007,56(9):5124-5130. ZHANG Chengfen, GAO Jinfeng, XU Lei. Chaos in fractional-order Liu system and a fractional-order unified system and the synchronization between them [J]. Acta Physica Sinica, 2007, 56(9): 5124-5130.

[8] 吳光強，黃煥軍，葉光湖. 基于分數階微積分的汽車空氣懸架半主動控制[J]. 農業機械學報, 2014, 45(7): 19-24. WU Guangqiang, HUANG Huanjun, YE Guanghu. Semi-active control of automotive air suspension based on fractional calculus[J].Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(7): 19-24.

[9] 孫會來，金純，張文明，等. 基于分數階微積分的油氣懸架建模與試驗分析[J]. 振動與沖擊, 2014, 33(17): 167-172. SUN Huilai, JIN Chun, ZHANG Wenming, et al. Modeling and tests for a hydro-pneumatic suspension based on fractional calculus[J].Journal of Vibration and Shock, 2014,33(17):167-172.

[10] PODLUBNY I. Fractional-order systems and PIλDμ-controllers[J].IEEE Transactions on Automatic Control,1999,44 (1):208-214.

[11] 柳向斌,曲曉麗. 分數階控制系統穩定性分析[J]. 河南科技大學學報,2007,28(2):33-36. LIU Xiangbin, QU Xiaoli. Stability analysis of fractional order control systems[J]. Journal of Henan University of Science & Technology,2007,28(2):33-36.

[12] 嚴慧，于盛林，李遠祿. 分數階PIλDμ控制器參數設計方法——極點階數搜索法[J].信息與控制, 2007(4): 445-450. YAN Hui, YU Shenglin, LI Yuanlu. A design method of the parameters of fractional-order PIλDμcontroller-poles-orders searching method [J]. Information and Control, 2007(4): 445-450.

[13] CHEN Y Q, PETRAS I, XUE D Y. Fractional order control—a tutorial [C]// 2009 American Control Conference Hyatt Regency Riverfront. St. Louis, MO, 2009.

[14] 薛定宇，趙春娜. 分數階系統的分數階PID控制器設計[J]. 控制理論與應用, 2007, 24(5): 771-775. XUE Dingyu, ZHAO Chunna. Fractional order PID controller design for fractional order system [J]. Control Theory & Applications, 2007, 24(5): 771-775.

[15] 黃麗蓮，周曉亮，項建弘. 分數階PID控制器參數的自適應設計[J]. 系統工程與電子技術, 2013, 35(5): 1064-1068. HUANG Lilian, ZHOU Xiaoliang, XIANG Jianhong. Self-adjusting design on parameters of the fractional order PID controller[J]. Systems Engineering and Electronics, 2013,35(5):1064-1068.

[16] OSTALCZYK P W, DUCH P, BRZEZISKI D W, et al. Order functions selection in the variable, fractional-order PID controller [J]. Lecture Notes in Electrical Engineering, 2015, 320:159-170.

[17] CHEN L C, ZHU W Q. Stochastic jump and bifurcation of duffing oscillator with fractional derivative damping under combined harmonic and white noise excitations [J]. International Journal of Non-Linear Mechanics,2011,46(10): 1324-1329.

[18] CHEN L C, LI Z S, ZHUANG Q J, et al. First-passage failure of single-degree-of-freedom nonlinear oscillators with fractional derivative[J]. Journal of Vibration and Control, 2013, 19(14): 2154-2163.

[19] LI C P, DENG W H. Remarks on fractional derivatives [J]. Applied Mathematics and Computation,2007,187(1): 777-784.

[20] 曹建雄,丁恒飛,李常品. 分數階擴散方程的隱差分格式[J]. 應用數學與計算數學學報,2013,27(1):61-74. CAO Jianxiong, DING Hengfei, LI Changpin. Implicit difference schemes for fractional diffusion equations[J]. Communicatin on Applied Mathematics and Computation, 2013,27(1):61-74.

[21] SANDERS J A, VERHULST F, MURDOCK J. Averaging methods in nonlinear dynamical systems[M]. New York:Springer, 2007.

[22] 申永軍，楊紹普，邢海軍. 含分數階微分的線性單自由度振子的動力學分析[J]. 物理學報, 2012, 61(11): 110505. SHEN Yongjun, YANG Shaopu, XING Haijun. Dynamical analysis of linear single degree-of-freedom oscillator with fractional-order derivative [J]. Acta Physica Sinica, 2012, 61(11): 110505.

[23] 申永軍，楊紹普，邢海軍. 含分數階微分的線性單自由度振子的動力學分析(Ⅱ) [J]. 物理學報, 2012,61(15): 110503. SHEN Yongjun, YANG Shaopu, XING Haijun. Dynamical analysis of linear single degree-of-freedom oscillator with fractional-order derivative [J]. Acta Physica Sinica, 2012, 61(15): 110503.

[24] MAGIN R L, RAWASH Y Z, BERBERAN-SANTOS M N. Analyzing anomalous diffusion in NMR using a distribution of rate constants[C]// Baleanu D, Machado JAT, Luo ACJ. Fractional Dynamics and Control. New York:Springer, 2012:263-274.

[25] SHEN Y J, YANG S P, SUI C Y. Analysis on limit cycle of fractional-order van der Pol oscillator [J]. Chaos, Solitons & Fractals, 2014, 67: 94-102.

Effect of a fractional-order PID controller on the dynamical response of a linear single degree-of-freedom oscillator

NIU Jiangchuan, SHEN Yongjun, YANG Shaopu, LI Sujuan

(School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

The free vibration of a linear single degree-of-freedom (SDOF) oscillator with a fractional-order PID controller of velocity feedback was investigated by the averaging method, and the approximately analytical solution was obtained. The results indicate that the effects of the parameters in the fractional-order PID controller on the dynamical properties are characterized. The proportional component of the fractional-order PID controller is characterized in the form of equivalent linear damping. The integral component of the fractional-order PID controller is characterized in the form of equivalent linear damping and equivalent linear stiffness. The differential component of the fractional-order PID controller is characterized in the form of equivalent linear damping and equivalent linear negative stiffness. Those equivalent parameters could distinctly illustrate the effects of the parameters in the fractional-order PID controller on the dynamical response. A comparison of the analytical solution with numerical results is made, and their agreement verifies the correctness of the approximately analytical results. The effects on system control performance of the coefficients and the orders in the fractional-order PID controller were analyzed by time response performance metrics parameters. Finally, the parameters tuning of the fractional-order PID controller based on velocity feedback was demonstrated through controlling a SDOF quarter vehicle suspension model.

fractional-order PID control; averaging method; approximately analytical solution

國家自然科學基金(11372198);河北省高等學校創新團隊領軍人才計劃(LJRC018);河北省高等學校高層次人才科學研究項目(GCC2014053);河北省高層次人才資助項目(A201401001)

2015-06-23 修改稿收到日期：2015-12-17

牛江川 男，博士，副教授，1977年生

申永軍 男，博士，教授，博士生導師，1973年生 E-mail：shenyongjun@126.com

O322；TP273

A

10.13465/j.cnki.jvs.2016.24.015