材料物性熱效應對統計能量分析參數的影響

張 鵬， 費慶國， 李彥斌， 吳邵慶

(1. 東南大學 江蘇省工程力學分析重點實驗室，南京 210096； 2. 東南大學 工程力學系，南京 210096)

材料物性熱效應對統計能量分析參數的影響

張 鵬1,2， 費慶國1,2， 李彥斌1,2， 吳邵慶1,2

(1. 東南大學 江蘇省工程力學分析重點實驗室，南京 210096； 2. 東南大學 工程力學系，南京 210096)

高溫環境會引起系統的統計能量分析參數發生變化，原因之一是溫度改變了材料物性。為建立計及材料物性熱效應的統計能量分析模型，有必要先研究材料物性熱效應對統計能量分析參數的影響。針對四周簡支的L形折板結構，在一板上施加雨流載荷(rain-on-the-roof)，計及材料物性熱效應，基于能量流模型分析得到子結構不同溫度下對應于特定模態群的載荷的平均輸入功率及各子系統的平均振動能量，再基于PIM理論分析得到由內損耗因子、耦合損耗因子與頻帶中心頻率的乘積定義的參數：內損耗系數、耦合損耗系數。研究結果表明：整體模態密度、雨流載荷的平均輸入功率與板材面內彈模隨溫度的變化趨勢相反；內損耗系數、耦合損耗系數與板材面內彈模隨溫度的變化趨勢相同。

統計能量分析；溫度效應；耦合損耗因子；功率流入射法；能量流模型

自從20世紀60年代美國麻省理工學院的LYON等[1]和英國的SMITH等[2]提出統計能量分析[3-4](Statistical Energy Analysis, SEA)理論以來，經過近60年的發展，該理論被廣泛地應用于航空航天、船舶潛艇、車輛、動力系統等領域的聲振環境預測，并取得了豐碩的成果。SEA方法的核心思想是忽略被研究系統的細節，對其隨機參量進行時域、頻域和空間統計，用統計參量來描述系統，并用能量這一獨立、通用的參量將各種動力學系統聯系在一起，也因此SEA方法特別適用于高頻激勵下復雜聲振耦合系統的響應預示。

SEA方法在響應預示過程中，主要涉及到四個參數：模態密度、內損耗因子(Damping Loss Factor，DLF)、耦合損耗因子(Coupling Loss Factor，CLF)以及輸入功率。為保證所建立的SEA分析模型的精度，準確獲取各參數取值一直是SEA理論發展的主要方向[5-8]。獲取CLF和DLF的方法有試驗分析方法、理論分析方法和仿真分析方法[9-11]，理論分析方法在一定程度上能滿足工程需求，但一般受限于簡單規則系統；試驗分析較難開展，尤其是涉及到高溫、高頻振動等環境時。除理論分析方法外，試驗分析方法和仿真分析方法大多是基于PIM[12](Power Injection Method)理論建立起來的，該方法的關鍵在于準確獲得各子系統在空間域和頻域上平均的能量。李湘南等[13]利用有限元計算各個有限單元振動速度的均方根，然后與各單元的集總質量求和，得出空間和頻域平均的子系統的能量；盛美萍等[14]利用結構平均導納來計算子系統的能量比，代入能量平衡方程得到耦合損耗因子和內損耗因子。前者的不足之處在于：由于要對結構各節點在每個頻帶步長下的位移或速度響應進行求和，計算量大；對于模態密度較大的柔性體，各節點的頻率響應在高模態密度下的不確定性增加，導致計算誤差增大。而后者存在的問題是，對于簡單子系統，其結構導納可以通過理論公式計算獲得，而對于復雜子系統則需要通過實驗來獲取。

高速飛行器服役中將面臨氣動加熱產生的高溫環境[15]，其會引起材料特性發生變化，即材料物性熱效應，同時氣動加熱使結構產生額外的熱應力，這兩個因素都會影響結構的振動特性[16]。楊雄偉等[17]以高超聲速飛行器X43A為例，研究了材料物性熱效應對聲振耦合特性產生的影響，研究顯示高溫引起的結構固有頻率降低導致聲振耦合特性的結構加速度響應峰值發生改變及位置漂移。李彥斌等[18]針對一復合材料加筋板分三個工況開展計及熱效應的聲-固耦合分析，研究顯示高溫引起的材料力學性能改變降低了板的固有頻率，使響應峰值升高并向低頻處移動。高溫環境產生的材料物性熱效應同樣會對高頻區的統計能量分析產生影響，為建立計及材料物性熱效應的統計能量分析模型，有必要先研究材料物性熱效應對統計能量分析參數的影響。

本文通過對節點響應的能量表達式進行模態分解，在模態坐標中建立能量流模型[19]，得到總系統及各子系統在隨機寬帶激勵下的能量。基于該能量流模型，考慮材料物性熱效應，將各子系統的振動能量代入能量平衡方程，求解得到各子系統在不同溫度下的內損耗系數和耦合損耗系數，并討論了溫度對載荷輸入功率、各子系統平均振動能量、內損耗系數以及耦合損耗系數的影響。

1 理論基礎

1.1 PIM理論

具有N個子系統的SEA模型動力學方程為：

(1)

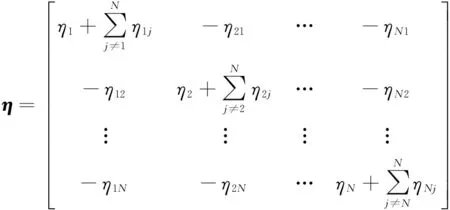
式中:ω為頻帶中心頻率，ηi為子系統i的DLF，ηij為子系統i到子系統j的CLF，Ei為子系統i內在空間和頻域的平均能量，pi為子系統i上在空間和頻域內平均的輸入功率。

當只在子系統i上施加輸入功率為pi的載荷時，有

(2)

式中:Eji表示只有子系統i受到載荷作用時子系統j在空間和頻域的平均能量。對于具有N個子系統的SEA模型，逐一在各子系統上施加載荷，并將所得到的形如式(2)的N個方程放到一起寫成矩陣形式，有

ωηE=p

(3)

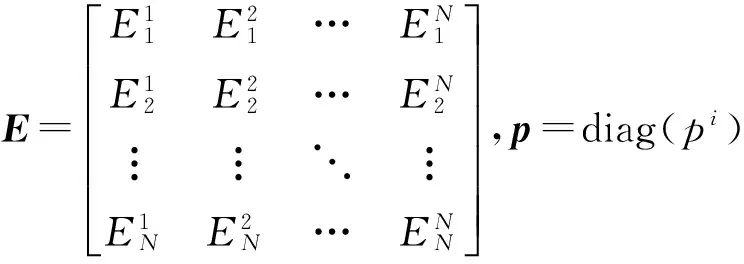
若式(3)中E和P為已知，可求得系數矩陣η，

(4)

進而可求得各子系統的DLF和各子系統間的CLF。

對于下文中的研究對象——典型L形折板(圖1所示)，當只有板1受到載荷作用時，有

(5)

式中:eij為子系統j上作用載荷時子系統i在頻段的平均能量，p1為施加于子系統1上載荷的輸入功率。

統計能量分析理論研究各子系統落在分析頻帶內的特定模態群間振動能量的耗散與傳遞。當溫度改變時，模態頻率會發生漂移，對應于常溫時分析頻帶內包含的模態群的中心頻率也會發生漂移，此時采用內損耗因子ηi和耦合損耗因子ηij表征系統的能量耗散和傳遞特性不再合理。此處定義內損耗系數：Mi=ηiω，耦合損耗系數：Mij=ηijω，改由內損耗系數Mi和耦合損耗系數Mij表征系統的能量耗散和傳遞特性，則式(5)可改寫為

(6)

式(6)中不包含頻帶的中心頻率ω，因此Mi和Mij可更直接地表征不同溫度下各子系統間對應于特定模態群的振動能量的耗散和傳遞特性。

由于該L形折板為一對稱結構，有η1=η2，η12=η21；進而有M1=M2，M12=M21；代入式(6)得

(7)

由式(7)可計算得到板1的內損耗系數及板1對板2的耦合損耗系數。

對于該典型的L形折板，也可通過理論分析計算每塊板的內損耗因子及兩板之間的耦合損耗因子[3,9]，進而計算獲得板1的內損耗系數M1和板1對板2的耦合損耗系數M12：

(8)

式中:ξ1為板1的平均模態阻尼比，CB為板彎曲波速，L為耦合邊長度，A為板面積，τ12為波傳遞系數。

1.2 能量流模型

由結點響應表示的系統振動的勢能T和動能V以及子系統b的勢能Tb和動能Vb如下：

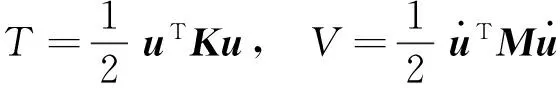
(9)

式中:K為總體剛度矩陣，M為質量矩陣，u為節點位移響應向量，下標b表示只包含子系統b內的自由度，ub是u的子集，可表示為ub=Sbu，Sb可稱為轉換矩陣。

通過模態分析可獲得基于質量矩陣歸一化的第j階模態振型向量φj和其對應的固有頻率ωj。根據模態的正交性有：PTMP=I，PTKP=diag(ωj2)，P=[φ1,φ2,…,φm]。在模態坐標系下的j階模態受到的載荷Fjy和對應的響應Yj為：

(10)

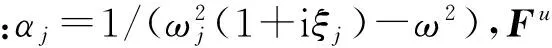
在模態坐標系下，子系統b的振動勢能和動能可表示為[19]

(11)

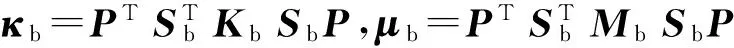
子系統a和子系統b皆為結構任一子系統。當只在子系統a上施加載荷Fu時，將式(10)代入式(11)并展開得子系統b的振動勢能和動能：

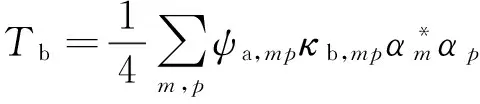
(12)

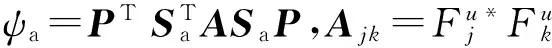
載荷的輸入功率為力與速度的乘積，在頻域內作用于子系統a上的載荷的輸入功率為：

(13)

1.3 雨流載荷

統計能量理論假設分析頻帶內各模態的振動能量相等，在后續分析過程中為滿足這一假設，宜選取對各模態輸入功率相近的載荷；雨流載荷[15]可以均等地、充分地激起子系統的局部模態(對各模態的輸入功率相等)，下面將在結構上施加該載荷進行分析。雨流載荷的定義為：空間各點不相關的寬帶激勵，任一點處載荷的幅值與該點的材料密度成正比。當結構被有限元離散后，雨流載荷對應的上述A矩陣與對應子系統的質量矩陣Ma成正比，即A=R2Ma，R表征該載荷的強度。在下面的分析過程中，對系統施加了單位雨流載荷。

2 數值算例

以典型的夾角成90°的L形折板為研究對象，對其進行了建模分析，如圖1所示。兩板尺寸均為300 mm×300 mm×1.5 mm，該結構的有限元模型采用殼單元進行模擬，單元尺寸為6 mm，除耦合邊外其余各邊簡支。

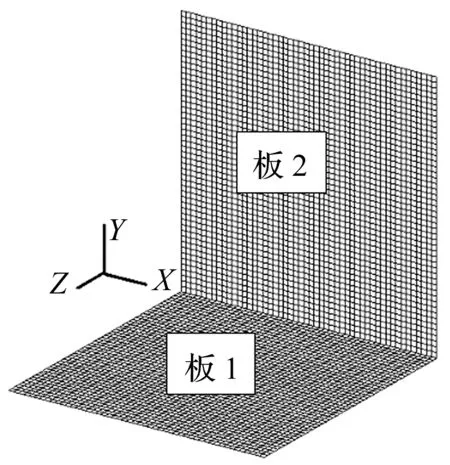
圖1 L形折板有限元模型Fig.1 The FE model of the L-plate

溫度變化可導致材料物性的變化，如彈模、泊松比和阻尼等，進而引起系統統計能量參數變化，其中材料彈模變化是引起系統統計能量參數變化的主要因素。下面研究材料彈模隨溫度變化對系統統計能量參數的影響。圖2給出由試驗測得的某板材面內彈性模量隨溫度的變化規律，分析過程中對各模態施加了阻尼比為2%的結構阻尼。

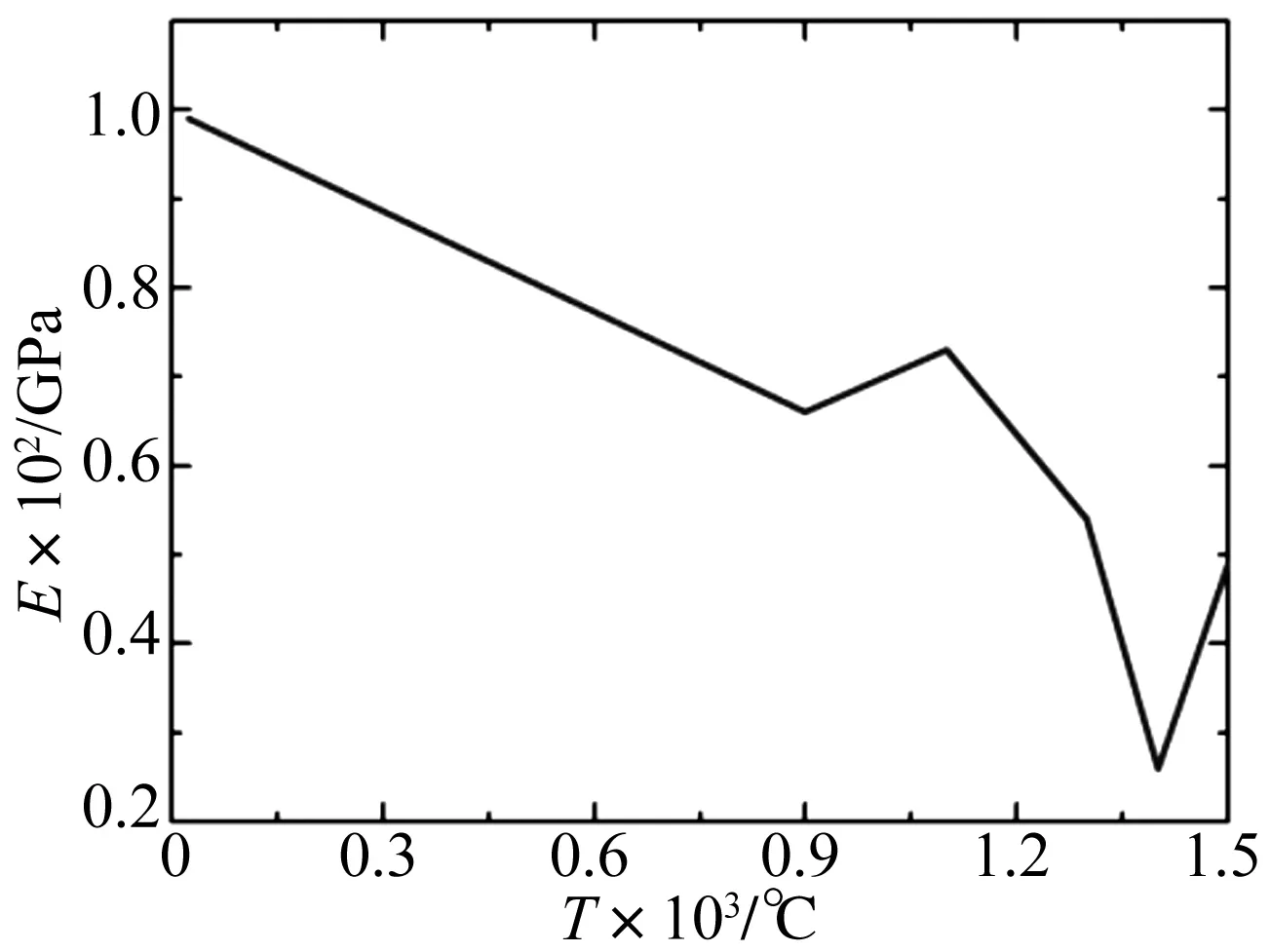
圖2 板材面內彈模隨溫度的變化Fig.2 The in-plane elastic modulus of the plate

2.1 模態分析

根據不同溫度條件(常溫、300℃、600℃、900℃、1 100℃、1 300℃、1 500℃)，采用對應的彈性模量進行模態分析獲得系統對應于各溫度條件的整體模態振型矩陣P及對應固有頻率。以模態固有頻率為縱坐標，模態階數為橫坐標，用一個“○”表示一階模態，繪出常溫時系統在0～6 000 Hz內的模態固有頻率的分布情況，如圖3所示，其中虛線為對各離散的模態進行線性擬合所得。

模態密度的含義為單位帶寬內的模態數，從圖3可以看出，在0～6 000 Hz內，模態密度幾乎為常值，即虛線斜率的倒數。系統對應于其他各溫度條件在0～6 000 Hz內的模態固有頻率的分布同圖3，此處不重復給出。

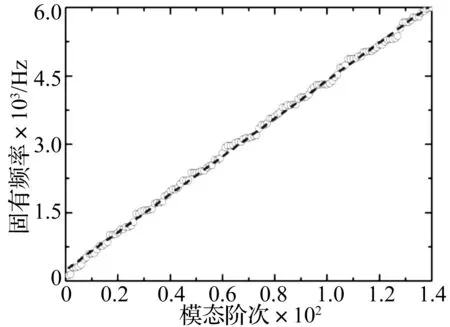
圖3 常溫下系統模態固有頻率的分布Fig.3 The distribution of the modal eigenfrequency of system at normal temperature

圖4給出系統在0～6 000 Hz內的模態數隨溫度的變化。從圖4可以看出系統在0～6 000 Hz內的模態數隨溫度的變化趨勢與板材面內彈模隨溫度的變化趨勢相反，這是由于整體模態密度隨溫度的變化趨勢與板材面內彈模隨溫度的變化趨勢相反。

圖4 不同溫度下系統在0～6 000 Hz內的模態數Fig.4 Number of modes in 0-6 000 Hz at different temperatures

2.2 輸入功率及振動能量

把L形折板劃分成兩個子系統：板1子系統和板2子系統。在板1上施加單位雨流載荷，通過分析獲得不同溫度時系統剛度矩陣和質量矩陣，進而基于0～6 000 Hz內的模態，由式(12)和式(13)計算得到0～3 500 Hz內兩板的振動能量和板1上載荷的輸入功率。圖5給出常溫時板1上載荷的輸入功率，其中虛線為在一定帶寬內平均的輸入功率。

從圖5可以看出，板1上載荷的輸入功率的各個峰值幾乎在同一量級，平均輸入功率在整個頻帶上分布平穩，近乎保持不變，這在一定程度上印證了1.3節所提到的雨流載荷對各模態的輸入功率相等。

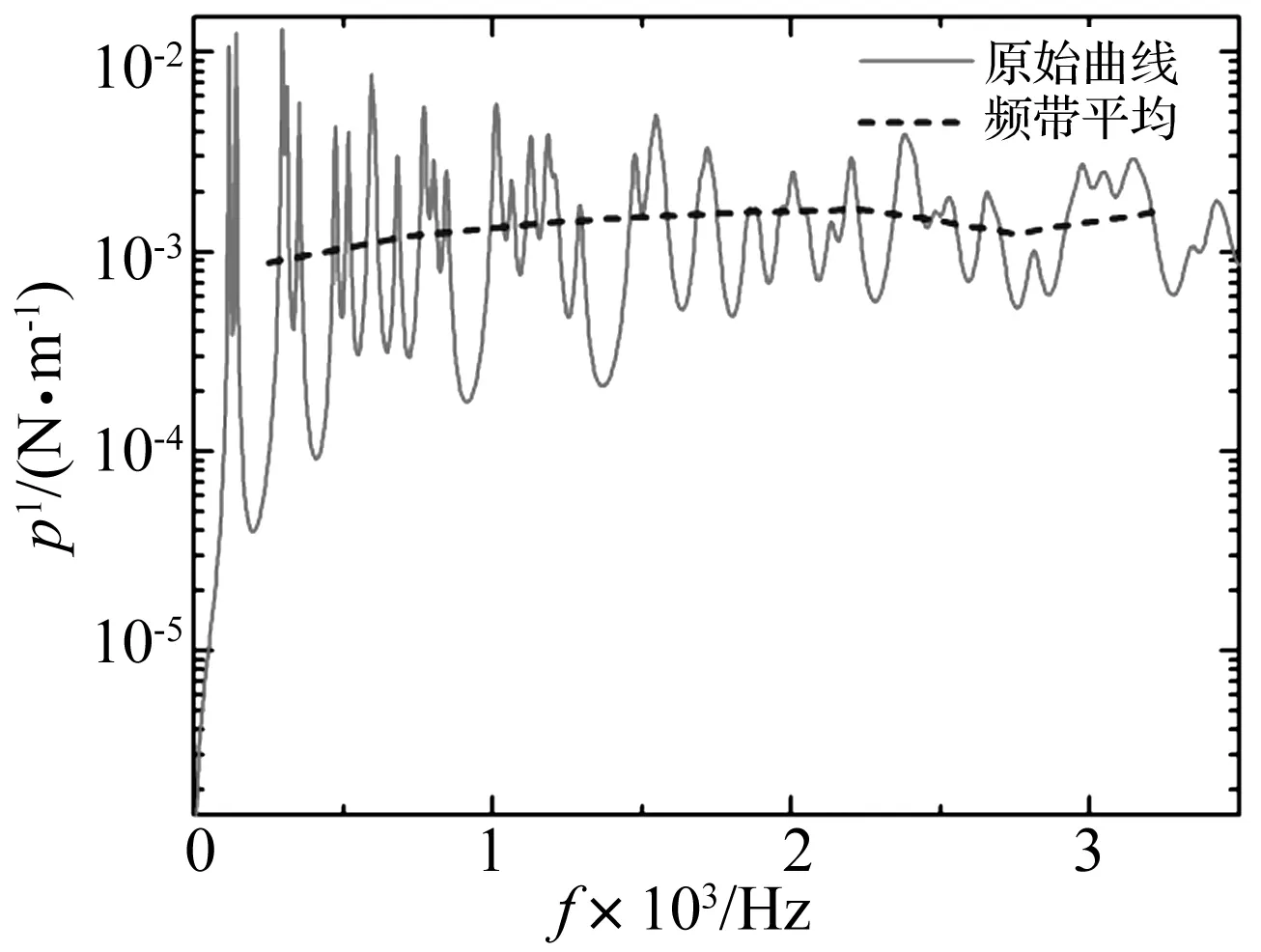
圖5 板1上載荷的輸入功率及平均輸入功率Fig.5 The input power of the load on plate-1

圖6給出常溫下板1的振動能量，其中虛線為在一定帶寬內平均的振動能量，可以看出平均振動能量隨頻率的變化比較順滑。

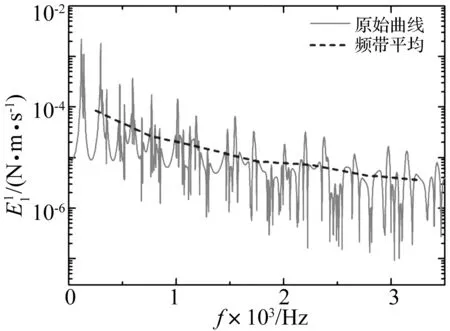
圖6 常溫下板1的振動能量及平均振動能量Fig.6 The vibration energy of plate-1 at normal temperature

統計能量分析理論要求落在分析頻帶Δω內的模態數不少于5，且只考慮落在Δω內的模態[3]。工程上通常根據載荷的頻域描述形式選取帶寬Δω，在高頻動響應預示領域最常見的是1/3倍頻程。后續分析中選取了中心頻率為2 000 Hz和3 150 Hz的兩個1/3倍頻程Δω1和Δω2。常溫時系統落在Δω1和Δω2內的模態數分別為10和18，滿足上述分析頻帶內模態數不少于5的要求。

分別記常溫時系統落在Δω1和Δω2內的模態群為N1和N2。統計能量分析理論研究各子系統間對應于特定模態群的振動能量耗散及傳遞特性，而隨著溫度的變化，落入Δω1和Δω2內的模態群也會發生變化，因此以下研究對應于特定模態群N1和N2的各參量隨溫度的變化規律。

圖7給出各溫度下施加于板1上對應于模態群N1和N2的平均載荷輸入功率，圖8為相應的板1和板2的平均振動能量。

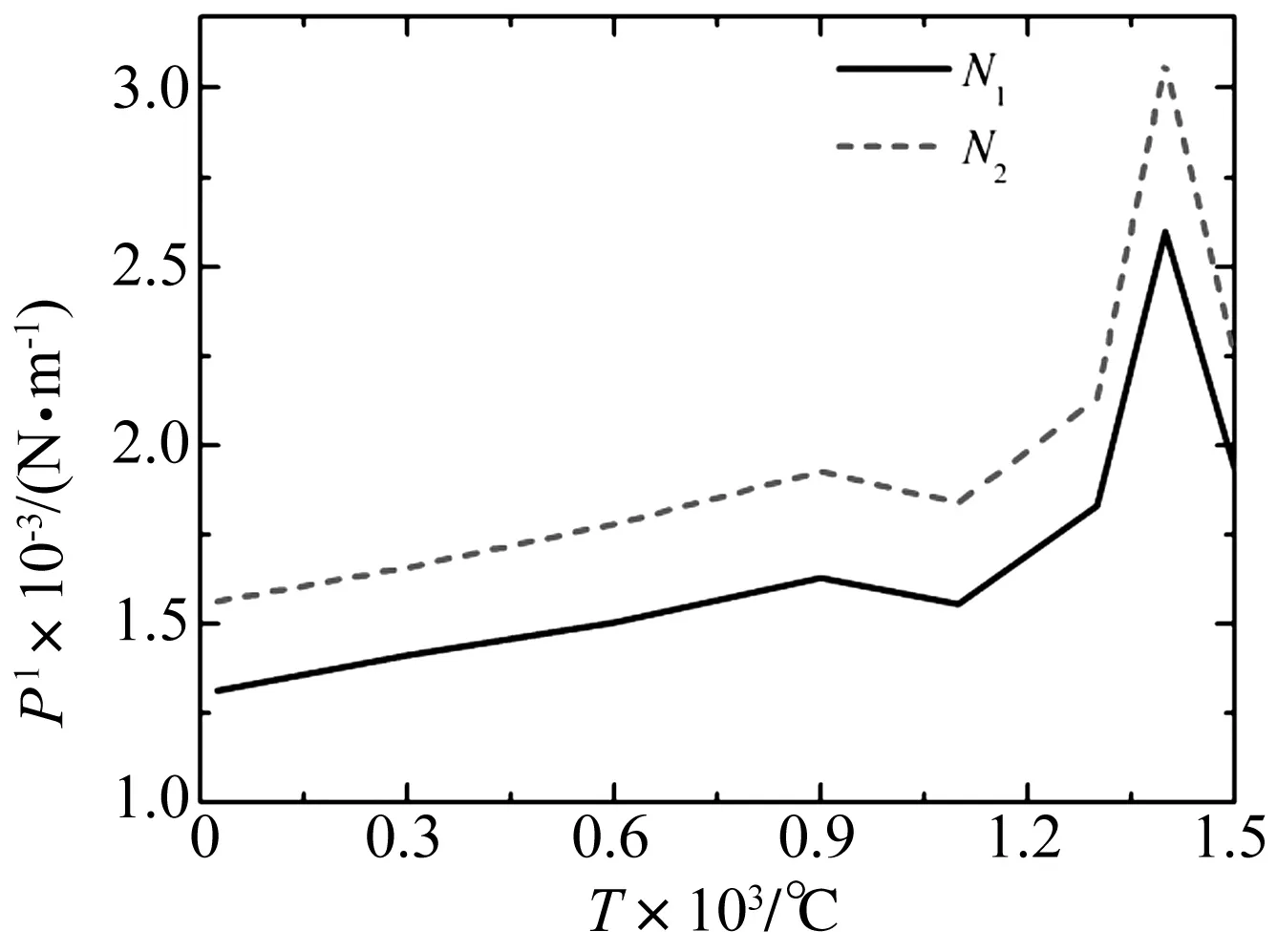
圖7 板1上平均輸入功率Fig.7 The frequency-averaged input power of plate-1

從圖7、圖8可以看出：對應于模態群N1和N2的板1上載荷平均輸入功率、兩板的平均振動能量隨溫度的變化趨勢均與板材面內彈模隨溫度的變化趨勢相反；載荷直接作用的板1上的平均振動能量比板2上的平均振動能量大。

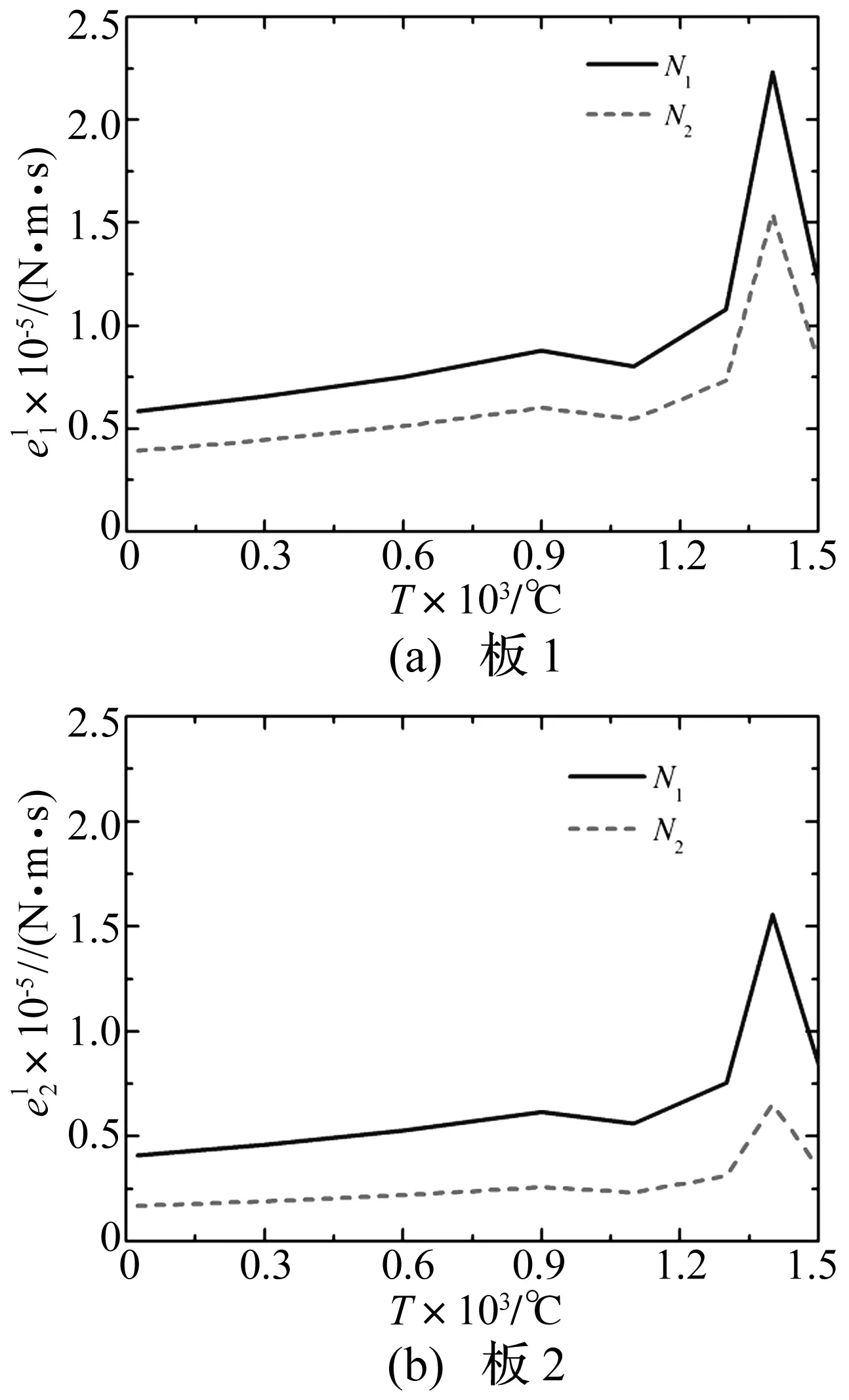
圖8 兩板平均振動能量Fig.8 The frequency-averaged vibration energy of plate-1 and plate-2

2.3 內損耗系數及耦合損耗系數

由式(7)計算得到板1的內損耗系數及板1對板2的耦合損耗系數(以后綴“PIM”標明)，并將該分析結果與由式(8)所示的理論分析方法所得結果(以后綴 “Analytical”標明)進行對比，如圖9、圖10所示。

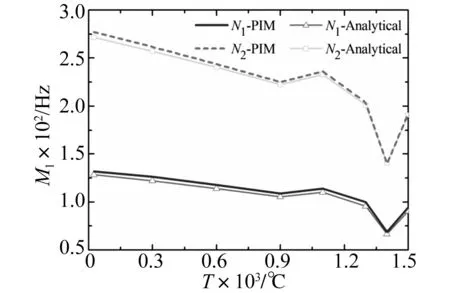
圖9 板1的內損耗系數Fig.9 The damping loss coefficient of plate-1

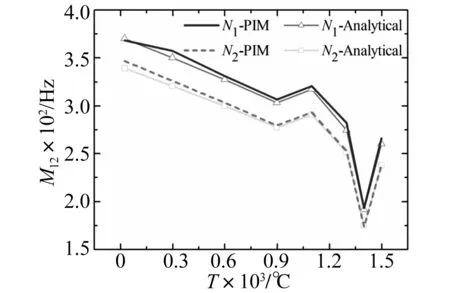
圖10 板1對板2的耦合損耗系數Fig.10 The coupling loss coefficient of plate-1 to plate-2

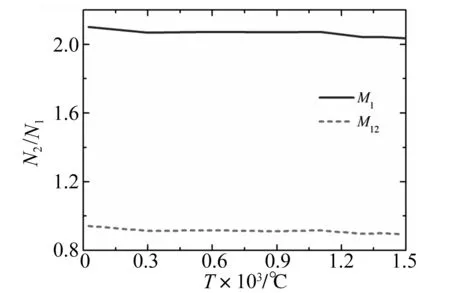
圖11 對應于模態群N2與N1的參量對比Fig.11 Comparison of parameters correspond to modal group N2 and N1

圖9、圖10中結果顯示：本文所采用的數值分析方法所得結果與理論分析方法所得結果一致，該數值分析方法所得結果可信；板1的內損耗系數和板1對板2的耦合損耗系數隨溫度的變化趨勢均與板材面內彈模隨溫度的變化趨勢相同；對應于頻率較高的模態群N2的內損耗系數顯著大于對應于頻率較低的模態群N1的內損耗系數，而對應于兩個模態群的耦合損耗系數大小相近。

圖11給出了對應于模態群N2和N1的內損耗系數以及耦合損耗系數的比值隨溫度的變化，從圖11可以看出，對應于模態群N2的內損耗系數和耦合損耗系數與對應于模態群N1的相應量的比值幾乎不隨溫度的變化而改變。

3 結 論

考慮溫度對材料彈性參數的影響，基于能量流模型和PIM理論，對兩個在一邊耦合、夾角成90°的平板所構成的典型L形折板模型進行數值仿真，在一個板上施加雨流載荷，分析獲得不同溫度時對應于特定模態群的載荷平均輸入功率、各子系統平均振動能量、內損耗系數以及耦合損耗系數，由理論分析方法所得結果驗證了本文所采用的數值分析方法所得結果。根據分析結果，對于該典型L形折板板模型，主要得出如下結論：

(1)整體模態密度隨溫度的變化趨勢與板材面內彈模隨溫度的變化趨勢相反；

(2)雨流載荷的平均輸入功率隨溫度的變化趨勢均與板材面內彈模隨溫度的變化趨勢相反；

(3)兩板的平均振動能量隨溫度的變化趨勢均與板材面內彈模隨溫度的變化趨勢相反；

(4)子系統的內損耗系數和子系統間的耦合損耗系數隨溫度的變化趨勢均與板材面內彈模隨溫度的變化趨勢相同；

(5)系統對應于不同模態群的內損耗系數以及耦合損耗系數之間的比值幾乎不隨溫度的變化而改變。

對于復雜系統計及材料物性熱效應的統計能量分析參數的獲取，理論分析方法不再適用，而本文所采用的數值分析方法對復雜系統具有良好的適用性。

[1] LYON R H, MAIDANIK G. Power flow between linearly coupled oscillators[J]. The Journal of the Acoustical Society of America, 1962, 34(5): 623-639.

[2] SMITH J P W. Coupling of sound and panel vibration below the critical frequency[J]. The Journal of the Acoustical Society of America, 1964, 36(8): 1516-1520.

[3] LYON R H, DEJONG R G, HECKL M. Theory and application of statistical energy analysis[J]. The Journal of the Acoustical Society of America, 1995, 98(6): 3021.

[4] 姚德源, 王其政. 統計能量分析原理及其應用[M]. 北京:北京理工大學出版社, 1995.

[5] XIE G, THOMPSON D J, JONES C J C. Mode count and modal density of structural systems: relationships with boundary conditions[J]. Journal of Sound and Vibration, 2004, 274(3): 621-651.

[6] UNGAR E E, KERWIN J E M. Loss factors of viscoelastic systems in terms of energy concepts[J]. The Journal of the Acoustical Society of America, 2005, 34(7): 954-957.

[7] SOUF B, BAREILLE O, ICHCHOU M N, et al. Variability of coupling loss factors through a wave finite element technique[J]. Journal of Sound and Vibration,2013,332(9): 2179-2190.

[8] D’AMICO R, KOO K, HUYBRECHS D, et al. On the use of the residue theorem for the efficient evaluation of band-averaged input power into linear second-order dynamic systems[J]. Journal of Sound and Vibration, 2013, 332(26): 7205-7225.

[9] PANKAJ A C, SASTRY S, MURIGENDRAPPA S M. A comparison of different methods for determination of coupling factor and velocity response of coupled plates[J]. Journal of Vibroengineering, 2013, 15(4): 1885-1897.

[10] JI L, HUANG Z Y. A simple statistical energy analysis technique on modeling continuous coupling interfaces[J]. Journal of Vibration and Acoustics, 2014, 136(1): 014501.

[11] LE BOT A, COTONI V. Validity diagrams of statistical energy analysis[J]. Journal of Sound and Vibration, 2010, 329(2): 221-235.

[12] BIES D A, HAMID S. In situ determination of loss and coupling loss factors by the power injection method[J]. Journal of Sound and Vibration, 1980, 70(2): 187-204.

[13] 李湘南, 林哲. 船舶機械設備聯接處非保守耦合損耗因子的研究[J]. 振動與沖擊, 2005, 24(4): 89-91. LI Xiangnan, LIN Zhe. Study on non-conservatively coupled loss factor of joints between ship mechanic equipment[J]. Journal of Vibration and Shock, 2005, 24(4): 89-91.

[14] 盛美萍, 王敏慶. 直接和間接耦合損耗因子的計算方法[J]. 噪聲與振動控制, 1997 (6): 2-7. SHENG Meiping, WANG Minqing. The calculation method of direct and indirect coupling loss factor[J]. Noise and Vibration Control, 1997 (6): 2-7.

[15] 孟松鶴, 丁小恒, 易法軍, 等. 高超聲速飛行器表面測熱技術綜述[J]. 航空學報, 2014, 35(7): 1759-1775. MENG Songhe, DING Xiaoheng, YI Fajun, et al. Overview of heat measurement technology for hypersonic vehicle surface[J]. Acta Aeronautica et Astronautica Sinica,2014,35(7): 1759-1775.

[16] 楊超, 許赟, 謝長川. 高超聲速飛行器氣動彈性力學研究綜述[J]. 航空學報, 2010, 31(1): 1-11. YANG Chao, XU Yun, XIE Changchuan. Review of studies on aeroelasticity of hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(1): 1-11.

[17] 楊雄偉, 李躍明, 閆桂榮. 考慮材料物性熱效應飛行器聲振耦合動態特性分析[J]. 固體力學學報, 2010, 31(增刊1):134-142. YANG Xiongwei, LI Yueming, YAN Guirong. Vibro-acoustic dynamic analysis of aircraft with temperature-dependent material property[J]. Chinese Journal of Solid Mechanics, 2010: 31(Sup1):134-142.

[18] 李彥斌, 張鵬, 吳邵慶, 等. 復合材料加筋板計及熱效應的聲-固耦合分析[J]. 振動工程學報, 2015, 28(4): 531-540. LI Yanbin, ZHANG Peng, WU Shaoqing, et al. Structural-acoustic coupling analysis of a composite stiffened panel in a thermal environment[J]. Journal of Vibration Engineering, 2015, 28(4): 531-540.

[19] MACE B R, SHORTER P J. Energy flow models from finite element analysis[J]. Journal of Sound and Vibration, 2000, 233(3): 369-389.

Effect of temperature-dependent material property on statistical energy analysis parameters

ZHANG Peng1,2, FEI Qingguo1,2, LI Yanbin1,2, WU Shaoqing1,2

(1. Jiangsu Key Laboratory of Engineering Mechanics, Southeast University, Nanjing 210096, China;2. Department of Engineering Mechanics, Southeast University, Nanjing 210096, China)

Environment temperature changes material property and then affects statistical energy analysis (SEA) parameters. It is necessary to study the effect of temperature-dependent material property on SEA parameters before establishing a SEA model with considering temperature. Firstly, the model of an L-shaped plate was created, which was simple supported at all sides. Secondly, the rain-on-the-roof load was applied on one plate of the L-shaped plate, and the frequency-averaged input power of load as well as the vibration energy of each sub-system at different temperatures corresponding to different mode sets was obtained based on the energy flow models. The effect of temperature-dependent material property was considered. Finally, the damping loss coefficient and coupling loss coefficient were defined by the product of the central frequency and the damping loss factor/coupling loss factor, respectively, based on the power injection method. Results show that the global modal density and the frequency-averaged input power of the rain-on-the-roof load are changing with the temperature and they have the contrary trend with the elastic modulus of the L-shaped plate verse temperature; the damping loss coefficients and coupling loss coefficients are changing with the temperature and they have the same trend with the elastic modulus of the L-shaped plate verse temperature.

statistical energy analysis; temperature effect; coupling loss factor; power injection method; energy flow models

國家自然科學基金(11572086；11402052)；教育部新世紀優秀人才支持計劃(NCET-11-0086)；江蘇省自然科學基金(BK20140616)；江蘇省普通高校研究生科研創新計劃資助項目(CXZZ13_0084)

2015-10-28 修改稿收到日期：2015-12-11

張鵬 男，博士生，1987年生

費慶國 男，教授，博士生導師，1977年生 E-mail: qgFei@seu.edu.cn

O327

A

10.13465/j.cnki.jvs.2016.24.012