淺議焦點三角形的內切圓

◇ 北京 岳昌慶

?

淺議焦點三角形的內切圓

◇ 北京 岳昌慶

如圖1所示,設△ABC內切圓I分別與AB、BC、CA相切于D、E、F,設BC=a,AC=b,BA=c.由初中平面幾何知識可得

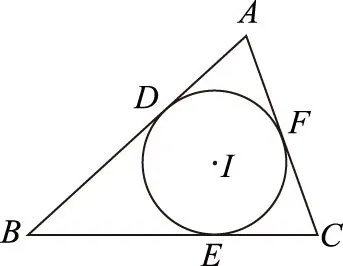
圖1

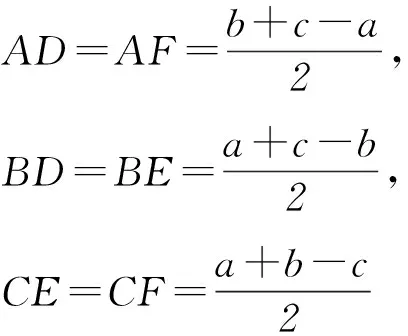
本文中的焦點三角形指橢圓或雙曲線上一點P與2焦點F1、F2所組成的△PF1F2.

1 雙曲線的焦點三角形

圖2

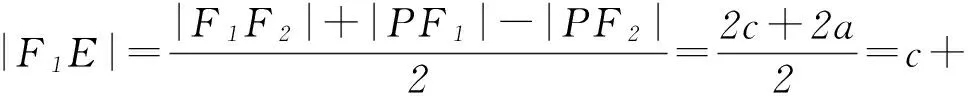
又|F1O|=c,所以|OE|=a,即E與A2重合.

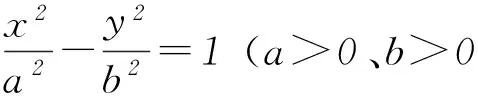
下面4個命題

① △PF1F2內切圓的圓心必在直線x=a上;

② △PF1F2內切圓的圓心必在直線x=b上;

③ △PF1F2內切圓的圓心必在直線OP上;

④ △PF1F2內切圓必通過點(a,0).

其中所有真命題的代號是________.

答案為①、④.

2 橢圓的焦點三角形

圖3

由三角形內角平分線定理及合、分比定理得

由焦半徑公式及線段的定比分點坐標公式得

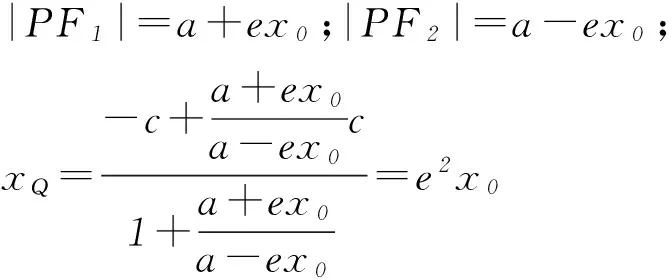
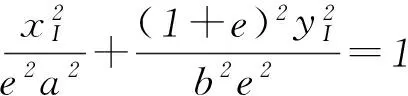
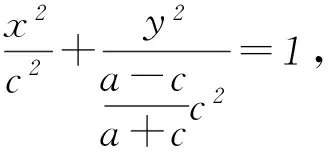
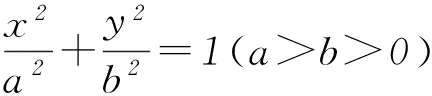
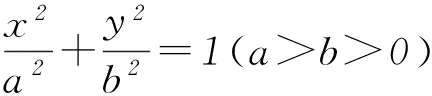
鏈接練習

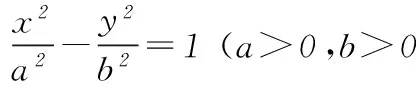
下面4個命題:

① △PF1F2內切圓的圓心必在直線x=-a上;

② △PF1F2內切圓的圓心必在直線x=-b上;

③ △PF1F2內切圓的圓心必在直線OP上;

④ △PF1F2內切圓必通過點(-a,0).

其中所有真命題的代號是________.

A2;B4;C1;D-1

鏈接練習參考答案

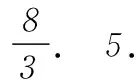
北京師范大學出版集團)