Duffing系統的雙參數分岔與全局特性分析

石建飛，張艷龍，王 麗，杜三山

（1.蘭州交通大學 機電工程學院，蘭州 730070； 2.蘭州城市學院 數學學院，蘭州 730070）

Duffing系統的雙參數分岔與全局特性分析

石建飛1，張艷龍1，王 麗2，杜三山1

（1.蘭州交通大學 機電工程學院，蘭州 730070； 2.蘭州城市學院 數學學院，蘭州 730070）

通過數值計算分析Duffing系統在雙參數平面上最大Lyapunov指數的分布特性，得到系統在雙參數平面上混沌運動、穩定周期運動和各種分岔曲線的參數區域，結合系統單參數分岔圖和相圖等，討論參數耦合對系統動力學特性的影響和系統在雙參數平面上的分岔與混沌過程。結果顯示在雙參數平面上由于混沌運動的參數區域被一系列的倍周期分岔曲線環包圍，導致系統單參數分岔圖出現連續周期泡結構，系統局部分岔特性變得非常復雜；在雙參數平面上，經叉式分岔后系統出現倍周期分岔等各種分岔曲線，使得系統經叉式分岔后出現各種吸引子共存現象，利用多初值分叉圖和胞映射法對系統經叉式分岔后的全局動力學特性進行詳細深入地研究，發現系統參數對各吸引子的穩定性和吸引子吸引域的演變規律有重要影響。

振動與波；Duffing系統；雙參數特性；分岔；Lyapunov指數；全局特性

20世紀80年代以來，對非線性系統的研究掀起了一股熱潮，作為典型的非線性系統模型，Duffing系統一直是國內外研究的熱點[1—7]，文獻[8]研究了Duffing系統在簡諧激勵下發生的對稱破裂分岔與激變現象；文獻[9]研究了兩個自由度并且含3次耦合項的Duffing系統在周期性作用力下的動力學；文獻[10]研究了Duffing系統在加性二值噪聲作用下的隨機分岔現象；文獻[11]研究了級聯雙穩Duffing系統的隨機共振特性；文獻[12]對基于可調頻Duffing振子的弱信號檢測方法進行了研究；文獻[13]研究了Duffing方程在隨機系數下的數值解問題；文獻[14]研究了強迫Duffing振子的反周期震蕩；文獻[15-17]對分數階Duffing系統的非線性動力學與混沌控制進行了一定的研究.文獻[18]對硬彈簧Duffing隔振系統的跳躍機理進行了研究。文獻[19]對Holmes型Duffing系統動力學特性進行仿真和實驗研究。近年來不少學者對Duffing系統進行了各種研究，并取得了大量研究成果[20-21]，但都研究系統在單參數條件下的動力學特性，在多參數條件下對Duffing系統分岔與混沌特性的研究卻鮮有文獻報道。對多參數耦合系統來說，系統在實際運動過程中不可能只受單參數的影響，而是各參數相互耦合共同作用的結果。故有必要研究Duffing系統在多參數耦合之下的動力學特性。

最大Lyapunov指數(top Lyapunov exponent，TLE)是判斷系統運動是否穩定最直接、最有效的方法之一，通過計算Duffing系統在雙參數平面上TLE的分布特性來研究系統在雙參數平面上的分岔混沌過程以及參數耦合對系統動力學特性的影響。在雙參數平面上系統出現周期跳躍、叉式分岔以及倍周期分岔等各種分岔曲線，系統經叉式分岔后出現吸引子共存現象，結合多初值分叉圖和胞映射法[22—23]對系統經叉式分岔后的全局動力學特性進行了深入地研究。

1 系統在雙參數平面上的分岔特性

研究如下Duffing方程

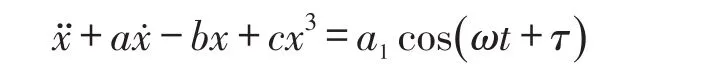
式中，無量綱參數a為阻尼系數、b為剛度系數、c為非線性項系數、a1為外激勵幅值、ω為外激勵角頻率、τ為初相位。給定a=0.83、b=1.0、c=0.5、τ=0.0，令ω和a1為參數變量，利用上述方法計算Duffing系統在雙參數平面ω-a1上最大李雅普諾夫指數的分布特性，如圖1所示。

圖1 系統在雙參數平面ω-a1上TLE特性分布

圖中深灰色區域為系統最大李雅普諾夫指數大于零的混沌區域；淺灰色區域為最大李雅普諾夫指數小于零的穩定周期區域；黑色實線或虛線表示系統最大李雅普諾夫指數近似等于零，當系統參數經過該曲線時，系統發生分岔或跳躍。由圖知，在不同參數耦合下系統運動特性不同，曲線PBi(i=1，2，3，4)為系統叉式分岔曲線，曲線DB1和DB2為倍周期分岔曲線，虛線S1為周期跳躍曲線；在曲線S1左邊系統出現兩條叉式分岔曲線PB2和PB3，當系統參數落在曲線PB2和PB3之間時，系統對初值具有較強的敏感性，即存在吸引子共存的現象（后面詳細分析），而在S1左邊其它區域內系統表現為穩定周期一運動；在曲線S1右邊系統出現了叉式分岔曲線PB1，隨ω的增加系統經PB1之后出現倍周期分岔曲線環DB1和DB2以及由倍周期分岔曲線環所包圍的混沌區域，在混沌區域內系統又出現了淺灰色周期區域和叉式分岔曲線PB4；在叉式分岔曲線PB1右邊整個區域內系統對初值具有較強的敏感性。系統參數經過叉式分岔曲線PB1后，系統在雙參數平面上的分岔特性變得非常復雜。下面結合單參數分叉圖具體分析。

在叉式分岔曲線PB1右邊區域內，由于系統在倍周期分岔曲線環內不斷嵌套倍周期分岔曲線環，導致系統最終經倍周期分岔序列進入混沌運動，造成系統單參數分岔具有連續的周期泡結構，保持其它參數與圖1一致，分別取a1的值為4.45、4.25、4.14和4.1，ω∈(1.8，2.8)計算系統隨ω變化的分岔圖如圖2所示，隨ω增加，圖2(a)系統由周期一倍化為周期二運動，后又退化為周期一運動；圖2(b)系統由周期一倍化為周期二運動，再由周期二倍化為周期四運動，后由周期四退化為周期二運動，最后由周期二退化為周期一運動；圖2(c)系統由周期一經倍周期分岔序列倍化為周期八運動，隨后由周期八運動經逆倍化分岔序列退化為周期一運動；圖2(d)系統由周期一經倍周期分岔序列進入混沌運動，隨后由混沌運動經逆倍化分岔序列退化為周期一運動；系統在雙參數平面上的分岔特性變得非常復雜。

在雙參數平面ω-a1上，系統在混沌區域內出現了淺灰色周期三區域，在該周期三區域內系統又出現了叉式分岔曲線PB4，在PB4左邊區域內系統周期三運動不穩定，對初值具有較強的敏感性；在PB4右邊區域內系統為穩定周期三運動。保持其它參數與圖1一致，取a1=2.65、ω∈(1.2，3)計算系統隨ω變化的分岔圖如圖3(a)所示，圖3(b)為其相應TLE圖。

隨ω的增加，系統經叉式分岔曲線PB1后由周期一運動經倍周期分岔序列進入混沌運動，對應圖1中系統經過叉式分岔曲線PB1后，經倍周期分岔曲線環DB1和DB2等進入混沌運動；當ω繼續增加時系統由混沌運動經逆倍周期分岔序列退化為不穩定的周期三運動，該周期三運動對初值具有較強的敏感性，在不同初值條件下系統相軌圖不同，其它參數保持不變，取ω=1.58計算系統在不同初值條件下的相圖如圖4(a)中粗實線和細實線所示；隨ω進一步增加，系統經過逆叉式分岔曲線PB4由不穩定周期三運動變為穩定周期三運動，其相圖如圖4(b)所示。

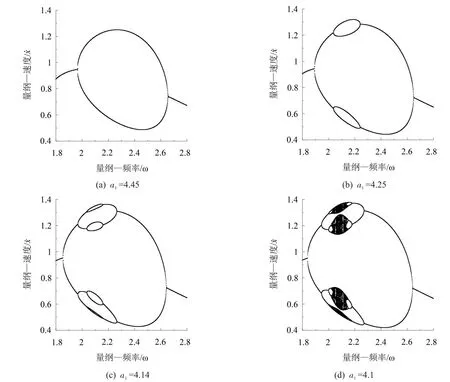
圖2 系統周期泡結構在ω∈(1.8， 2.8)時系統單參數分叉圖

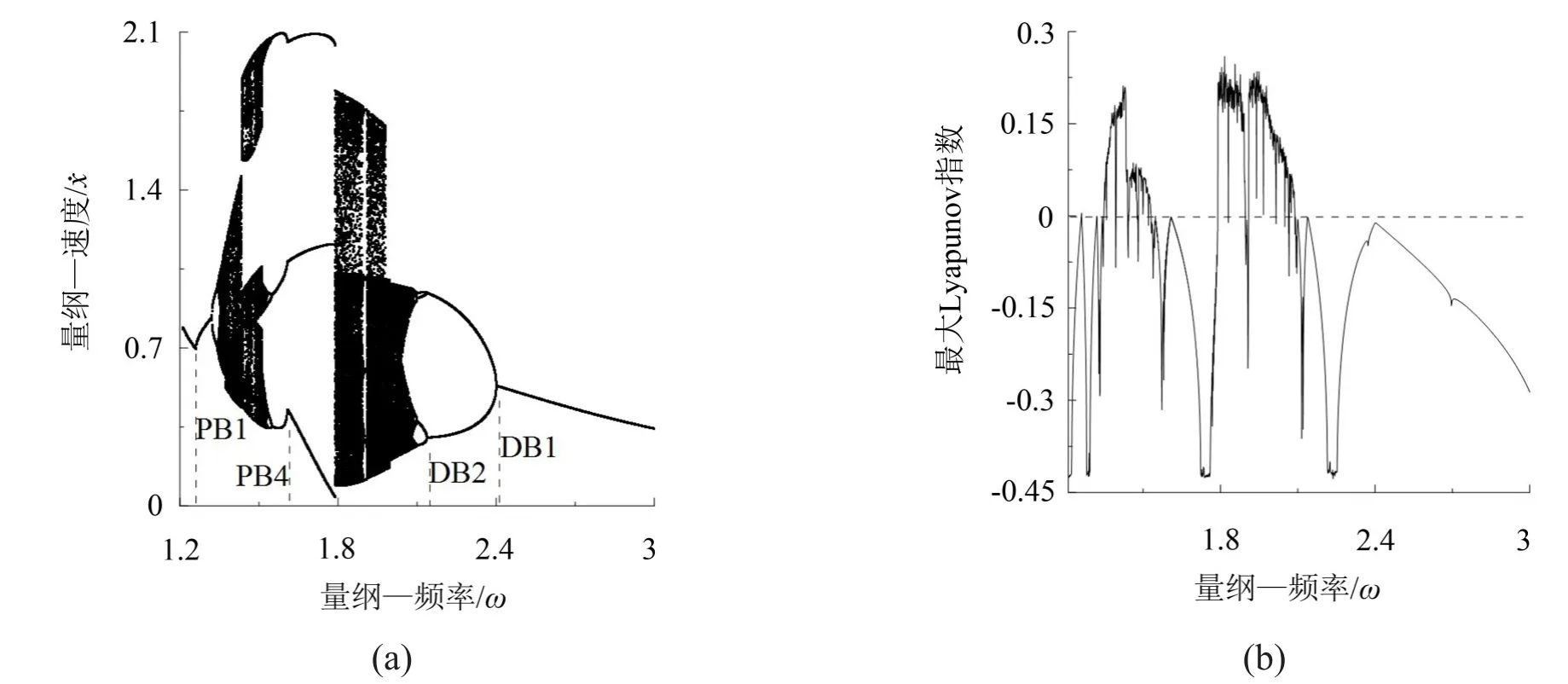
圖3 a1=2.65、ω∈(1.2，3.0)時系統單參數分叉圖和相應TLE圖

隨ω繼續增加，系統由周期三運動進入混沌運動，最后經逆倍化分岔序列退化為穩定周期一運動，對應圖1中，隨ω的增加系統由混沌運動經倍周期分岔曲線環退化為穩定周期一運動。圖3系統分岔點位置及分岔趨勢與圖1中當a1=2.65、ω∈(1.2，3)時相吻合。

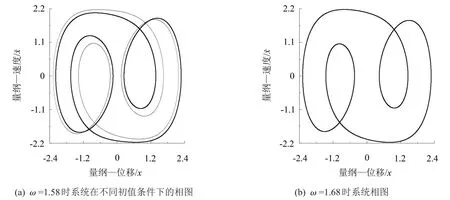
圖4 系統相圖

由以上分析得知，通過計算系統在雙參數平面上的TLE得到系統在雙參數平面ω-a1上各種分岔曲線、穩定周期運動以及混沌運動的參數區域；在周期跳躍曲線S1左邊，系統在大部分參數區域內為穩定周期一運動，而在叉式分岔曲線PB2和PB3之間的參數區域內系統為不穩定周期一運動；在周期跳躍曲線S1右邊，經叉式分岔曲線PB1后系統出現倍周期分岔曲線環DB1、DB2等和由這些倍周期分岔曲線所包圍的混沌運動，在混沌區域內系統又出現了周期三運動和叉式分岔曲線PB4，使得系統在曲線S1右邊部分參數范圍內的分岔特性變得極為復雜。

2 系統全局動力學特性分析

在圖1中保持其它參數不變，取a1=5.1計算系統隨ω變化的單參數分岔圖和相應TLE圖如圖5(a)和5(b)所示。

圖5(a)中隨ω的增加，系統在ω=0.787時發生叉式分岔，對應圖1中叉式分岔曲線PB2，系統單參數分岔圖出現缺邊現象，隨ω繼續增加，當ω=0.897時系統發生逆叉式分岔，其缺邊現象消失，對應圖1中叉式分岔曲線PB3；當ω增加到1.771時系統發生一次跳躍，跳躍前后系統均為周期一運動，對應圖1中的周期跳躍曲線S1；ω進一步增加，當ω=1.914時系統再次發生叉式分岔，其單參數分岔圖出現缺邊現象，對應圖1中叉式分岔曲線PB1；隨ω進一步增加，當ω=2.223時系統發生倍化分岔，由周期一運動倍化為周期二運動，隨后當ω=2.625時系統發生逆倍化分岔，由周期二退化為周期一運動，對應圖1中，隨ω的增加，系統先后經過倍周期分岔曲線環DB1。由以上分析知，系統單參數分岔圖與圖1相對應；在雙參數平面上系統經過叉式分岔曲線后，其單參數分叉圖出現缺邊現象，系統對初值具有較強的敏感性，在不同初值條件下系統可能會運動到不同的吸引子上。下面利用多初值分岔圖并結合簡單胞映射法對系統全局動力學特性進行詳細分析。

圖5 a1=5.1、ω∈(0.05，3.5)時系統單參數分叉圖和相應TLE圖

圖5(a)中保持其它參數不變，分別取ω∈(0.7，1.0)和ω∈(1.5，3.5)計算系統隨ω變化的多初值分叉圖如圖6(a)和圖6(b)所示，系統在多初值條件下其分叉圖上經叉式分岔點后缺失的邊出現，表明系統在該叉式分岔點后出現多吸引子共存現象。

圖6(a)中，保持其它參數不變，取ω=0.8，研究考擦區域定義為x∈(-5，5)、∈(-5，5)，利用簡單胞映射法計算系統在考察區域內各吸引子的吸引域如圖7(a)所示，圖中白色+代表周期一P1的吸引子，淺灰色區域為其吸引子的吸引域；白色×代表另一周期一Q1的吸引子，黑色區域為其吸引子的吸引域；由圖知淺灰色區域與黑色區域形狀相似且相互嵌套在一起，黑色區域面積較淺灰色大，表明系統在該考擦區域內吸引子Q1的穩定性較P1強。

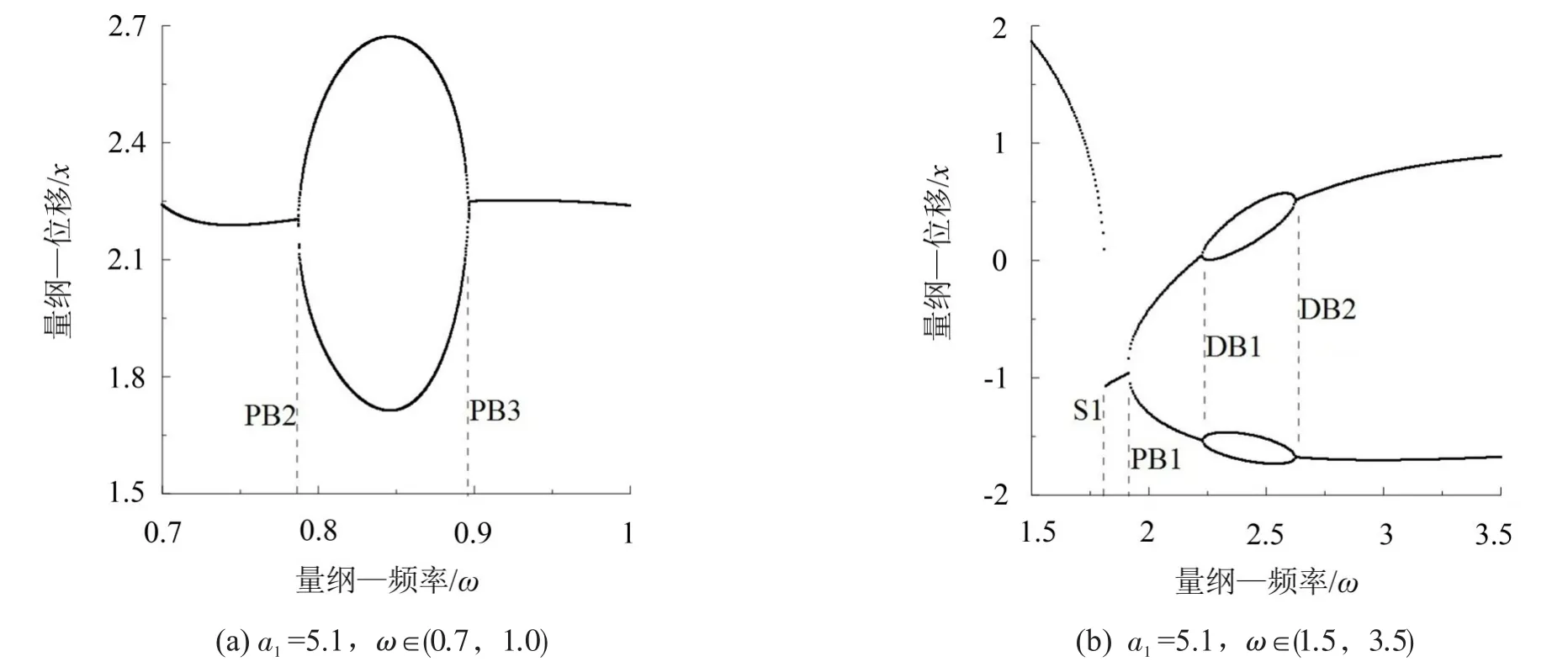
圖6 系統多初值分岔圖

圖6(b)中，當ω=1.914時系統經過叉式分岔曲線PB1，出現兩周期一吸引子共存的現象，隨ω的增加，當ω=2.223時系統發生倍化分岔，出現了兩個周期二吸引子共存的現象，當ω=2.625時系統發生逆倍化分岔，系統又出現了兩個周期一吸引子共存的現象。保持其它參數不變，分別取ω的值為2.15、2.5和2.75計算系統在考察區域x∈(-3，3)、∈(-3，3)內各吸引子的吸引域分別如圖7(b)、7(c)和7(d)所示。

在圖7(b)中存在兩周期一吸引子P1和Q1共存的情況，其中白色×代表周期一P1的吸引子，淺灰色區域為其吸引子的吸引域；白色+代表周期一Q1的吸引子，黑色區域為其吸引子的吸引域。由圖知淺灰色區域與黑色區域相互嵌套并纏繞在一起，表明系統在該參數條件下兩吸引子的全局動力學特性都不穩定，初值的稍微變動都能使系統運動到不同的吸引子上；在圖7(c)中，由于倍化分岔的原因系統存在兩周期二吸引子P2與Q2共存的情況，其中白色×為P2的吸引子，淺灰色區域為其吸引子的吸引域；白色+為Q2的吸引子，黑色區域為其吸引子的吸引域；對比7(b)，在圖7(c)中各吸引子吸引域的相互嵌套和纏繞度有所降低，各吸引子的吸引域不斷集中，其穩定性有所增強，此外在考察區域內各吸引子吸引域的形狀由中心向外不斷擴大；在圖7(d)中，由于逆倍化分岔的原因，系統又出現兩周期一吸引子共存的現象，對比圖7(b)和7(c)，各吸引子吸引域的形狀由中心向外逐漸擴展，且各吸引子吸引域的分布變得比較集中，使各吸引子穩定性逐漸提高。

由以上分析得知，系統經過叉式分岔后出現吸引子共存現象，通過計算系統各吸引子吸引域發現其吸引域的拓撲結構相似且相互嵌套并纏繞在一起，使得系統穩定性降低；隨參數ω的增加，各吸引子吸引域不斷集中，且由中心向外逐漸擴展，使得系統各吸引子的穩定性有所增強。

3 結語

給出了系統在參數空間TLE的計算方法，這種方法不但計算簡單而且實用性很強，對高維系統同樣適用。數值計算了Duffing系統在雙參數平面上TLE的分布特性，得到系統在雙參數平面上混沌運動、穩定周期運動和各種分岔曲線的參數區域；結合單參數分岔圖和相圖，詳細分析了系統在雙參數平面上的分岔混沌過程，在雙參數平面上混沌運動的參數區域被一系列倍周期分岔曲線環包圍，導致系統單參數分岔圖具有連續的周期泡結構；在混沌運動參數區域內，系統出現了周期三運動參數區域和叉式分岔曲線PB4，周期三區域被曲線PB4分成左右兩部分，左邊區域周期三運動不穩定，右邊區域周期三運動穩定。

利用多初值分岔圖和簡單胞映射法，對系統經叉式分岔后的全局動力學特性進行了詳細深入的分析，在多初值條件下在分岔圖上系統經叉式分岔后缺失的邊出現；系統叉式分岔點之后存在多吸引子共存現象，通過計算各吸引子的吸引域，詳細深入地研究了各吸引子在考察區域內的穩定性以及隨ω變化時各吸引子吸引域的演變規律。研究發現隨ω的增加系統各吸引子的穩定性逐漸增強，各吸引子的吸引域面積不斷集中。

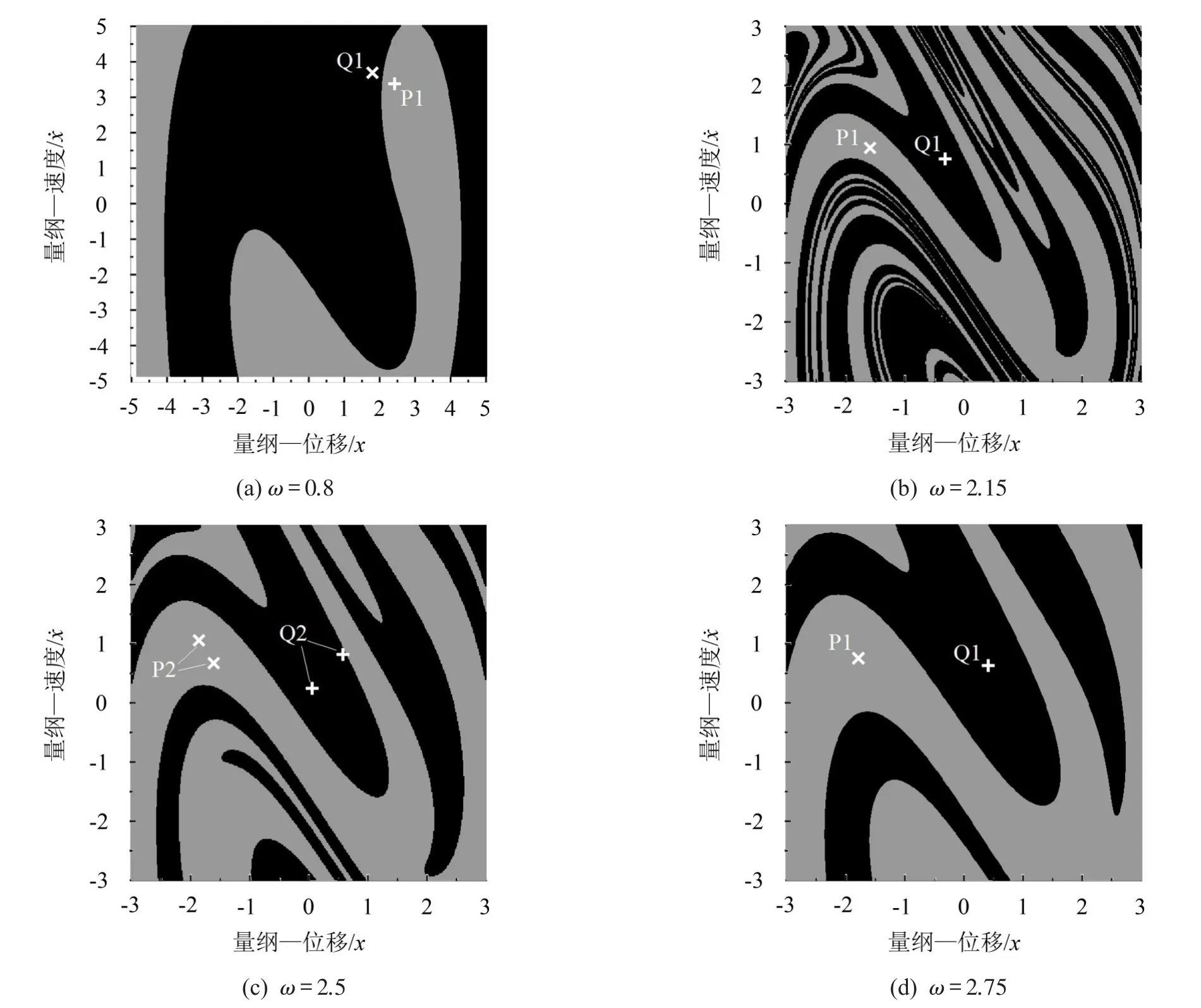
圖7 吸引子的吸引域

利用系統在參數平面上TLE的分布特性來研究非線性系統具有一定的有效性和可行性，以上研究對多參數耦合系統在較寬條件下的非線性動力學行為研究及混沌控制具有參考價值。

[1]JIAN Z P.Advanced feedback control of the chaotic duffing equation[J].IEEE Trans.Circuits Syst.I.,2002, 49(2):244-249.

[2]XU H B,LU B C,CHEN G J.Chaotic control of the doffing equation in the presence of uncertainty[J].Systems Engineering and Electronics,2000,22(2):15-16.

[3]LI ZENGSHAN1,CHEN DIYI,ZHU JIANWEI1,et al. Nonlinear dynamics of fractional order Duffing system[J].Chaos,Solitons and Fractals,2015,81:111-116.

[4]MARCIN KAMI?SKI,ALBERTO CORIGLIANO. Numerical solution of the Duffing equation with random coefficients[J].Meccanica,2015,50(7),1841-1853.

[5]PEIJUN JU.Global residue harmonic balance method for Helmholtz-Duffing oscillator[J].Applied Mathematical Modelling,2015,39(8),2172-2179.

[6]樓京俊，何其偉，朱石堅.多頻激勵軟彈簧型Duffing系統中的混沌[J].應用數學和力學，2004，25(12)，1299-1304.

[7]唐元璋，樓京俊，翁雪濤，等.Duffing振子倍周期分岔譜特性[J].振動與沖擊，2014，33(2)：60-63.

[8]張瑩，李爽.重訪Duffing系統中的對稱破裂分岔與激變[J].西北工業大學學報，2015，33(1)：88-92.

[9]曹振邦，樂源.兩個自由度Duffing系統的分岔及混沌分析[J].重慶理工大學學報(自然科學)，2015，29(10)：79-82.

[10]武娟，許勇.加性二值噪聲激勵下Duffing系統的隨機分岔[J].應用數學和力學，2015，36(6)：593-599.

[11]賴志慧，冷永剛，范勝波.級聯雙穩Duffing系統的隨機共振研究[J].物理學報，2013，62(7)：070503(1-9).

[12]MA SONGSHAN,LU MING,DING JIAFENG,et al. Weak signal detection method based on Duffing oscillator with adjustable frequency[J].Science China Information Sciences,2015,58(10):1-9.

[13]MARCIN KAMI?SKI,ALBERTO CORIGLIANO. Numerical solution of the Duffing equation with random coefficients[J].Meccanica,2015,50(7):1841-1853.

[14]SHAW PANKAJ KUMAR,JANAKI M S,IYENGAR A N S,et al.Antiperiodic oscillations in a forced Duffing oscillator[J].Chaos,Solitons and Fractals,2015,78:256-266.

[15]曹軍義，謝航，蔣莊德.分數階阻尼Duffing系統的非線性動力學特性[J].西安交通大學學報，2009，43(3)：50-54.

[16]韋鵬，申永軍，楊紹普.分數階Duffing振子的亞諧共振[J].振動工程學報，2014，27(6)：811-818.

[17]何桂添，羅懋康.分數階Duffing混沌系統的動力性態及其由單一主動控制的混沌同步[J].應用數學和力學，2012，33(5)：539-552.

[18]樓京俊，張暉，俞翔等.硬彈簧Duffing隔振系統跳躍機理分析[J].噪聲與振動控制，2014，34(6)：20-24.

[19]孫方旭，劉樹勇，何其偉.Holmes型Duffing系統動力學特性仿真及實驗[J].噪聲與振動控制，2016，36(2)：17-26.

[20]JIFENG CHUA,FENG WANGAB.Prevalence of stable periodic solutions for Duffing equations[J].Journal of Differential Equations,2016,260(11):7800-7820.

[21]JAUMELLIBREA,ANA RODRIGUESB.A nonautonomous kind of Duffing equation[J].Applied Mathematics and Computation,2015,251:69-674.

[22]HSU C S.Cell-to-cell mapping:A method of global analysis for nonlinear system[M].New York:Springer-Verlag,1987.

[23]HSU C S.A theory of cell-to-cell mapping dynamical systems[J].Journal of Applied Mechanics,1980,147: 931-939.

Double-parameter Bifurcation and Global Characteristic Analysis of Duffing Systems

SHI Jian-fei1,ZHANG Yan-long1,WANG Li2,DU San-shan1
(1.School of Mechanical Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China; 2.School of Mathematics,Lanzhou City University,Lanzhou 730070,China)

The distribution characteristics of the Top Lyapunov exponent of Duffing systems on the double-parameter plane are calculated.The parameter areas of the chaotic motion,the stable periodic motion and the various bifurcation curves are obtained on the double-parameter plane.Combined with the system single-parameter bifurcation diagram and the phase diagram,the bifurcation and chaos process on the double parameter plane and the influence of parameter-coupling on system dynamic performance are discussed.The results show that the parameter region of the chaotic motion is surrounded by a series of double periodic bifurcation curves,therefore the continuous bubble structures appear in the system single-parameter bifurcation diagrams and the local bifurcation characteristics become very complicated.In the double parameter plane, various bifurcation curves,for example the period-doubling bifurcation curves,occur after the pitchfork bifurcation curve, which leads to the phenomenon of various attractors coexistence after the pitchfork bifurcation.The system global dynamic characteristics are studied by using multi-initial value bifurcation diagrams and the cell-to-cell mapping method.It is found that the system parameters have an important influence on the stability of the attractors and the evolution of the attractor domains.

:vibration and wave;Duffing system;double-parameter character;bifurcation;Lyapunov exponent;global dynamic characteristic

O322

：A

：10.3969/j.issn.1006-1335.2016.06.007

1006-1355(2016)06-0032-06+50

2016-06-08

國家自然科學基金項目(11302092)

石建飛（1990-），男，甘肅省隴南市人，碩士生，主要研究方向為非線性動力學及控制。E-mail:sjf0214286@126.com

張艷龍（1981-），男，河北省圍場縣人，副教授，碩士生導師。E-mail:zhangyl@mail.lzjtu.cn