機載LiDAR點云定量化局部結構信息分析

曹志民，谷延鋒，吳 云

（1.東北石油大學 電子科學學院，黑龍江 大慶163318；2.哈爾濱工業大學 電子與信息工程學院，黑龍江 哈爾濱 150001）

機載LiDAR點云定量化局部結構信息分析

曹志民1,2，谷延鋒2，吳 云1

（1.東北石油大學 電子科學學院，黑龍江 大慶163318；2.哈爾濱工業大學 電子與信息工程學院，黑龍江 哈爾濱 150001）

提出一種基于特征值的機載LiDAR數據定量化局部信息量分析方法。通過引入多項策略改進了傳統主成分分析（PCA）點云局部結構分析對噪聲敏感的缺點，利用這種魯棒性很強的PCA局部結構分析結果，從信息論的角度給出了一種點云局部結構定量化分析的新方法。實驗結果表明，該方法能夠有效實現對機載LiDAR點云數據結構信息量的有效分析。

主成分分析；機載LiDAR；局部結構分析

由于機載激光雷達LiDAR具有主動獲取目標大量具有精確三維空間坐標點云數據的能力，已經在攝影測量及遙感、電力系統、石油勘探等多個研究領域得到廣泛應用[1-5]。通過提取機載LiDAR點云數據的局部結構信息，可以實現特定目標的三維結構重建。其中，基于特征值的方法是進行目標結構特征分析的一種典型方法[6-9]。然而，傳統的基于PCA的局部結構特征值分析方法對點云數據中存在的噪聲及干擾非常敏感。為了解決傳統PCA方法的噪聲敏感性，已經有很多學者提出了相應的改進方法。這些改進方法主要可以分為2種類型：①改進局部鄰域的選擇方法; ②改進局部協方差矩陣的構造方法。本文從局部鄰域選擇及局部協方差矩陣計算的可靠性出發，實現了一種對噪聲具有較強魯棒性的PCA局部結構分析方法。利用該方法得到的分析結果，從信息論出發，實現了LiDAR點云數據局部結構信息量的定量化計算。

1 機載LiDAR數據定量化局部結構信息分析

1.1 基于PCA的局部結構分析

對于給定點云數據P∈RN×3，令Pi∈R1×3（1≤i≤N）為點云數據中一個給定的點，局部結構分析的目的是判斷該點屬于點、線、面或體狀結構，如圖1所示。首先定義一個關于該點的鄰域NBi={pj|dist（pj，pi）＜T}，即在距離測度dist（·）下，到點pi的距離小于閾值T的所有點的集合。在得到鄰域Nbi后，即可通過計算鄰域協方差矩陣Qi∈R3×3，利用PCA技術分析其局部結構：

式中，pNBi為鄰域中所有點的均值。

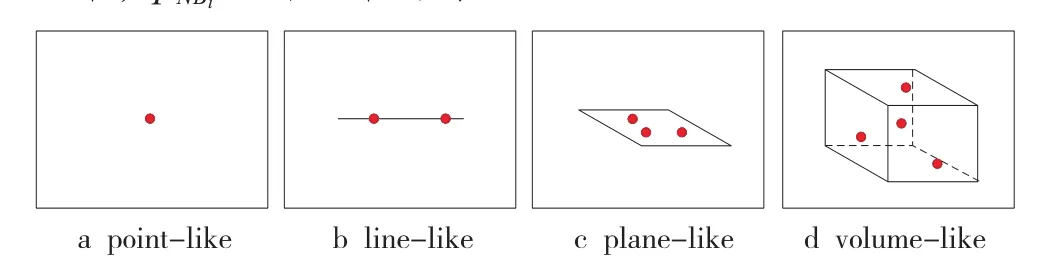
圖1 3D形狀分析示意圖

利用PCA技術對式（1）得到的協方差矩陣進行特征值分析，可以得到3個特征值λ1、λ2、λ3（λ1≥λ2≥λ3）。根據特征值間的相對大小關系，即可實現對點云局部結構的分析。當最大特征值λ1很小時，局部結構為點狀；當最大特征值λ1不是很小，而λ2和λ3都很小時，局部結構為線狀；當只有λ3很小時，局部結構為面狀；當所有3個特征值都不是很小時，局部結構為體狀。另外，除了直接利用3個特征值的大小外，還可以通過3者的組合構造多種典型特征值，

1.2 局部結構信息定量化分析

理論上，§1．1所述基于PCA技術的特征值局部結構分析能夠很好地實現點云局部結構的判斷。而實際應用中，由于數據采集設施中不可避免的隨機誤差及數據采集過程中外界環境等因素的影響，原始點云數據會存在各種隨機噪聲干擾，而§1．1所述的經典PCA法對噪聲是非常敏感的。為此，本文通過如下4個措施來增強基于特征值的局部結構分析方法的魯棒性：①原始數據進行歸一化處理，增強計算的魯棒性；②利用近似最近鄰ANN技術，利用黎曼圖結構構造局部鄰域；③利用L1Median算法獲取的幾何中值代替協方差計算中的均值；④選取對噪聲具有強魯棒性的特征值Cλ作為局部結構分析的依據。

至此，即可利用上述魯棒特征值分析的結果從信息論的角度出發進行定量化局部結構信息的計算，該定量化局部結構信息也可以看作是一種結構顯著性特征。本文中，局部點結構往往是一些野值點造成的，而野值點可以通過簡單的預處理得到篩除。為此，典型局部結構以線、面、體結構為主。若令原始點云中任一點pi為線、面、體結構的概率分別為pl、pp和pc，那么定義該點的局部結構信息量為：

式中，wpl、wpp和wpc分別為原始點云中線、面及體結構的總體概率。

本文提出的基于特征值的局部結構信息量定量化分析方法具體步驟如下：

步驟 1：利用ANN算法得到原始點云P∈RN×3中每個點的局部鄰域點標號集Ids∈Rk×N（k為ANN鄰域點個數）及鄰域點到對應中心點的距離矩陣Ds∈Rk×N。

步驟 2：初始化結構計數矩陣SCl， SCp，SCc∈RN×1為0N×1，不同結構的結構概率矩陣Pr∈RN×3為0N×1。

步驟 3：利用本文提出的魯棒性PCA局部結構分析方法及步驟1得到的局部鄰域知識進行局部結構投票：對于任一點pi及其鄰域NBi中的鄰域點，利用局部幾何中值構造協方差矩陣進行PCA分解，得到對應的特征值，并計算點pi所在鄰域的局部曲率變化。如果＜0.05，則：

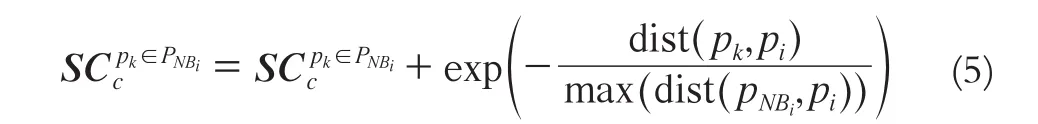
步驟 4：計算定量化局部結構信息量矩陣QI∈RN×1。為了得到QI， 首先需要得到不同結構在原始點云數據中的總體概率：

其中符號·/表示元素對元素的點除運算。最終，有：

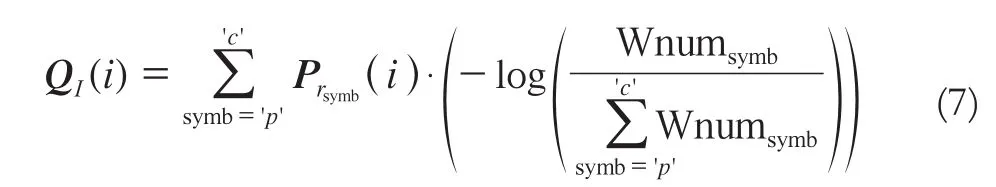
式中，Wnumsymb表示Prsymb中概率值大于0的個數。

2 實驗結果

為了驗證本文所提方法的有效性，以結構信息豐富的建筑物屋頂點云為例，分別利用仿真數據和實際數據進行驗證。

本文所采用的仿真數據包括2個典型的具有豐富點線結構的建筑物屋頂模型，都是由100 701個點構成，點間距為0．01 m，如圖2a所示。除了仿真數據外，還選取3個具有不同結構細節的真實機載LiDAR點云數據，如圖2b～2d所示。其中第一個真實數據采樣密度約為2點/平面，共2 621點，第2和第3個真實數據采樣密度均為6．7點/km，分別有18 516點和19 845點。

圖2 實驗數據示意圖

利用所提定量化局部結構信息分析方法，對圖2所示4組數據的實驗結果如圖3所示(第一列為原始數據的正視圖；第二列為曲率變化特征；第三列為定量化信息量) 。

圖3 定量化結構信息分析結果

3 結 語

通過增強基于傳統PCA技術的點云數據局部結構信息分析方法對噪聲的魯棒性，增強了這種典型的基于特征值點云數據局部結構分析的有效性和實用性。另外，從信息論的角度更深層次地挖掘點云數據局部結構信息，能夠以一種定量化形式輸出，得到局部結構顯著性分析結果，為后續結構信息的充分利用提供了有效支持。

[1] Lemmens M． Airborne LiDAR Sensors [J]． GIM International, 2007, 21(2): 24-27

[2] Yan J, Shan J, Jiang W． A Global Optimization Approach to Roof Segmentation from Airborne LiDAR Point Clouds[J]．ISPRS Journal of Photogrammetry and Remote Sensing, 2014(94): 183-193

[3] 李峰, 吳燕雄，衛愛霞,等． 機載激光雷達3維建筑物模型重建的研究進展[J]．激光技術,2015,39(1):23-27

[4] 高敏,韓聰． 基于機載激光雷達技術的城市三維數據建設[J]．測繪與空間地理信息,2014,37(11):134-135

[5] Zhang W, Wang H． 3D Building Roof Modeling by Optimizing Primitive's Parameters Using Constraints from LiDAR Data and Aerial Imagery[J]．Remote Sensing, 2014(6):8 107-8 132

[6] Sampath A, Shan J． Segmentation and Reconstruction of Polyhedral Building Roofs from Aerial LiDAR Point Clouds[J]． IEEE Trans on Geoscience and Remote Sensing, 2010, 48(3):1 554-1 567

[7] Gross H, Thoennessen U． Extraction of Lines from Laser Point Clouds[J]． International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2006(36):86-91

[8] Fransens J, Reeth F． Hierarchical PCA Decomposition of Point Clouds[C]． 3DPVT'06, Chapel Hill, NC, 2006

[9] Lin C H, Chen Y Y, Su P L． Eigen-feature Analysis of Weighted Covariance Matrices for LiDAR Point Cloud Classification[J]．ISPRS Journa of Photogrammetry and Remote Sensing, 2014(94):70-79

P237.3

B

1672-4623（2016）02-0010-03

10.3969/j.issn.1672-4623.2016.02.003

曹志民，博士，講師，主要研究方向為遙感多源數據融合與處理。

2015-03-18。

項目來源：國家自然科學基金資助項目（61371180）;東北石油大學培育基金資助項目（基于信息化稀疏表示的三維建筑物LiDAR數據復原）。