單片空間后方交會內部可靠性研究

吳 磊

（1.廣東省國土資源測繪院，廣東 廣州 510500）

單片空間后方交會內部可靠性研究

吳 磊1

（1.廣東省國土資源測繪院，廣東 廣州 510500）

根據Baarda的可靠性理論，以空間后方交會為實驗模型，在平差過程中引入虛擬控制點和控制點整體平差，并運用數據探測法進行單個粗差探測。實驗表明，加入虛擬控制點，能適當提高每個觀測值上的多余觀測分量，減小控制點上粗差可發現的下界值。使用Baarda數據探測法檢測粗差更有效，提高了該平差系統的內部可靠性。當網形結構不好、多余觀測分量過少時，這種方法還能探測到數據探測法不能探測到的粗差。

空間后方交會；數據探測法；內部可靠性；粗差探測

由于各種因素的影響，觀測值中常帶有一定數量的粗差，如果對數據直接處理，會損壞參數估計的精度。因此，平差中需要探測粗差并排除或減弱粗差對數據處理的危害[1]。荷蘭Baarda教授在1967年首先提出了平差系統的可靠性理論，并導出了數據探測法[2]；陶本藻在相關權陣基礎上，從方差比檢驗出發，構建了一種新的數據探測法[3]；陶本藻、施闖等針對相關觀測的粗差探測，提出了一種基于相關分析的粗差理論，為多維相關觀測粗差的檢測開辟了一條新途徑[4,5]；於宗儔直接從最小二乘平差系統中的觀測誤差與殘差的關系出發，提出了多個粗差同時定位定值的方法[6]。

Baarda提出的測量平差系統中的單個模型誤差的可靠性理論已在大地測量、攝影測量、工程測量及變形觀測中得到廣泛的應用，而從單個模型誤差到多個模型誤差，從單一備選假設到2個備選假設的發展，由于研究較為復雜，目前尚未得到廣泛的應用[7]。本文遵循Baarda的可靠性理論與數據探測基本思想，以航空攝影測量空間后方交會為實驗模型，從觀測值的單個粗差出發，提出了一種外方位元素的求解方案。

1 基于虛擬觀測的空間后方交會平差模型

1.1 虛擬控制點的提出

一個平差系統的圖形結構設計好后，在一定的觀測精度下，給定顯著性水平σ0和檢驗功效β0，則系統發現每個點上粗差的下界是確定的。在航空及航天攝影測量中，由于航高及控制點分布的原因，導致圖形結構可能很壞，圖形結構的直接反映就是誤差設計矩陣A，如果能改善圖形結構，就可能增強系統的可靠性。本文提出了通過布設虛擬點，改善圖形結構，然后和地面控制點整體平差，并人為對控制點引入粗差，使用數據探測法檢測。

1.2 虛擬控制點的模擬及平差過程

通過最小二乘平差迭代求得的外方位元素值、隨機生成的像點坐標（xv，yv）以及給定的虛擬點深度范圍（Zmin，Zmax），利用共線方程可以生成虛擬點（Xv，Yv），此時每個虛擬點的像點坐標（xv，yv）及三維坐標（Xv，Yv，Zv）都已知，把虛擬點當作觀測值和控制點一起參與下次平差。每一次迭代后通過新的外方位元素生成虛擬點（Xv，Yv），再次平差解算，如此循環，直到收斂輸出。未知參數估計的概略流程圖如圖1。

1.3 函數模型

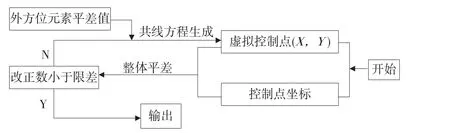
圖1 平差流程圖

帶虛擬控制點的后方交會誤差方程為：

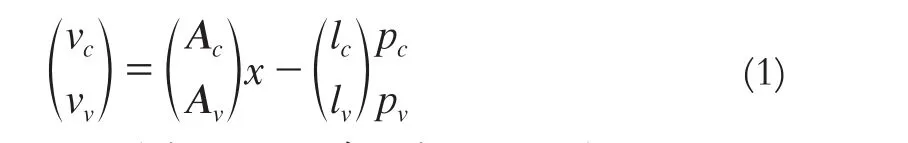
式中，pc、pv分別為控制點和虛擬控制點的權。

由于虛擬控制點的（Xv，Yv）是在迭代過程中根據外方位元素最新解算值不斷更新的：

當虛擬點參與下次平差逐點組成誤差方程并法化時，可計算出lv：

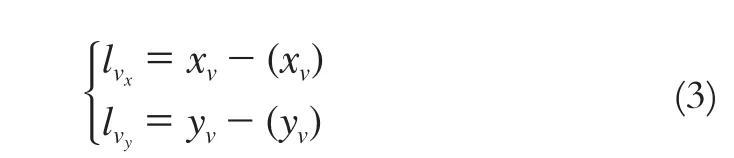
其中，

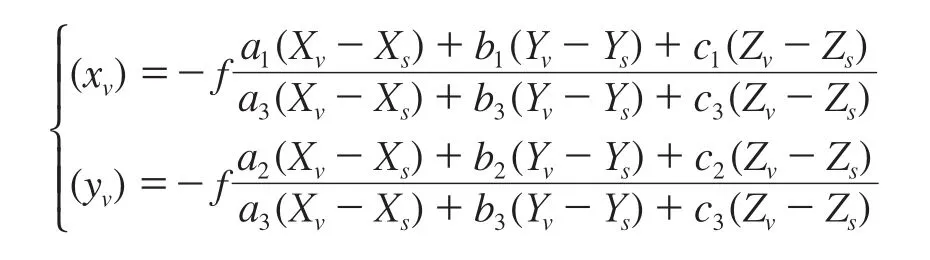
因此可知：

誤差方程式（1）可變為：

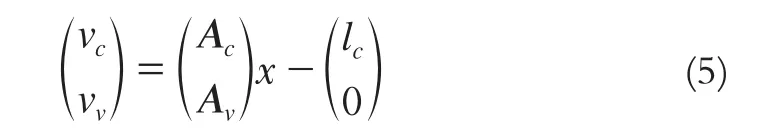
此時方程的解為：

與嚴格的最小二乘間接平差模型解相比，N陣多了一項：AvTPvAv。若虛擬控制點也是真實控制點，此時外方位元素的最小二乘解為：

1.4 參數的精度評定與數據探測

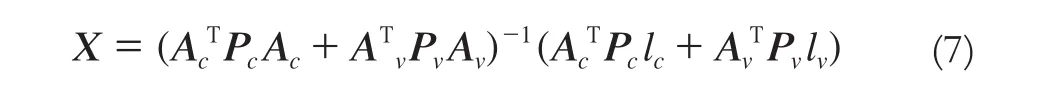
當lv≠0，即使用式（7）計算X時，QVV陣有如下形式：

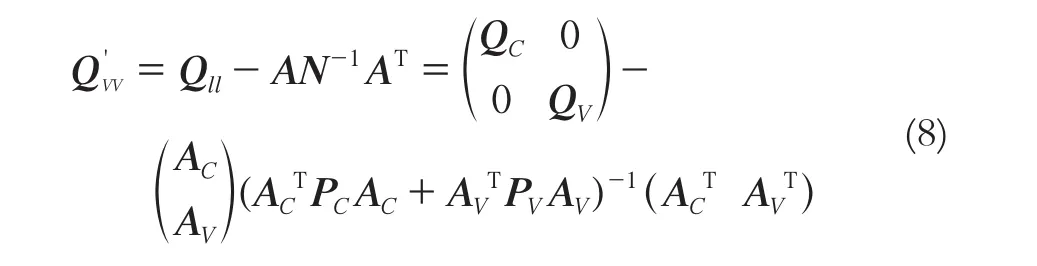
當lv=0時，顧及式（5）與式（6），根據協因數傳播定律，可以得到：

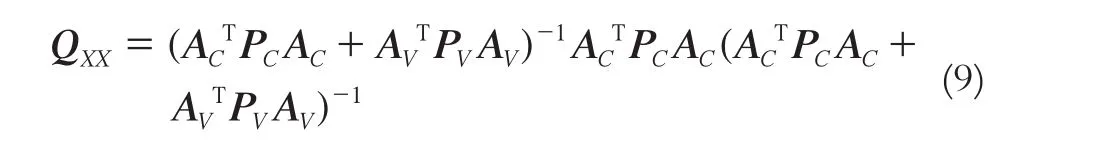
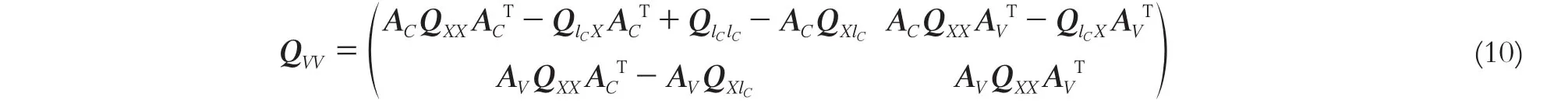
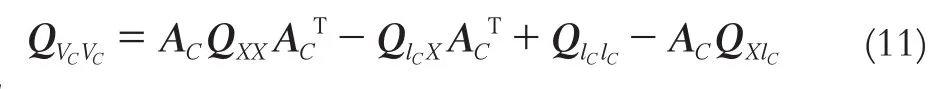
其中，

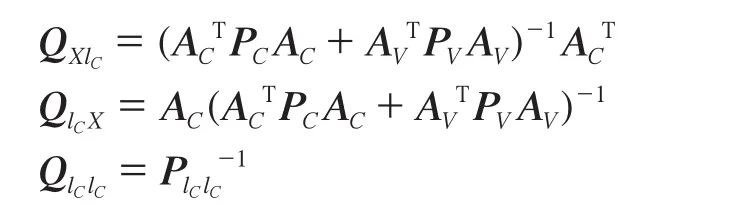
當觀測值只存在一個粗差時，構建標準殘差統計量，使用數據探測法對其檢驗：

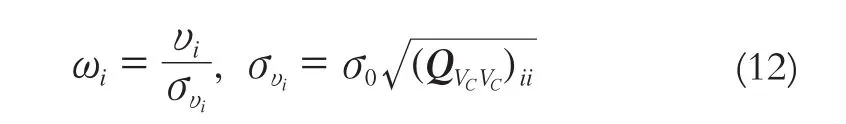
其中，

式中，r=2n-6；n為控制點和虛擬控制點總個數。

給定閾值Ka，當ωi≥Ka，則認為該觀測值可能含有粗差。平差時計算出每個控制點上的統計量ωi，再根據給定閾值進行粗差檢測，文中給定Ka=3.29。

1.5 可靠性指標[1]

在一個平差系統中，對于單個備選假設下的可靠性，設模型誤差為單個觀測值上的粗差，給定顯著性水平α0和檢驗功效β0，可得到一個粗差被發現的下界值：

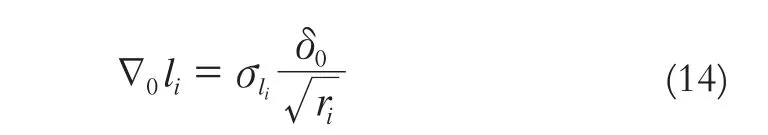
式中，ri=（QVVPll）ii，為第i個觀測值的多余觀測分量；δ0為非中心化參數；σli為第i個觀測值的中誤差。

文中還將用到可控性數值：

1.6 實際平差解算方法與過程

平差時，外方位元素的估計值嚴格上應使用式 （6）算出，此時觀測值殘差V與測量誤差l間關系式V=- （QvvPll）l不再成立；若使用式（7）計算，平差的幾何條件QvvPll反映了觀測值誤差對改正數的作用程度。由于該矩陣為冪等矩陣，具有一系列性質，從中可以直接得到每個觀測值的多余觀測分量。如果使用式（6）計算，Qvv則具有式（10）的形式，此時QvvPll矩陣顯然不是冪等矩陣，其對角線元素不再反映多余觀測分量。為了方便分析問題，文中可靠性指標多余觀測分量、可控性數值、粗差探測下限中改正數向量的協方差陣Qvv使用式（8）計算，此時理解為把生成的虛擬控制點加入很小的正態隨機誤差，這樣lv便不再為0，求出的QvvPll為冪等矩陣，對角線元素反映了多余觀測分量。而使用Baarda數據探測法進行粗差探測時，標準化殘差統計量ωi按照式（12）構建，其中改正數向量的協方差陣QVV按式（10）計算。

2 算 例

2.1 實驗數據說明

選用某地區航空區域網內的一張航片為實驗數據，航片的外方位元素由光束法區域網平差求得，由于一張航片覆蓋范圍內不可能有大量控制點，因此在本文實驗中，把相片覆蓋范圍內的加密點當作控制點使用。選用了相片近似標準點位的9個加密點，從而可以反解得6個外方位元素。相機為框幅式相機；幅面大小為108．000 mm×72．000 mm；像素大小為0．009 mm。

平差過程中參數說明如下：

1）外方位角元素光束法平差值為：φ=1.286 5°，ω=1.060 2°，κ=-5.547 8°，在有無虛擬控制點2種情況下的初始角元素值都取為：φ=0°，ω=0°，κ=0°。

2）進行了6點法和9點法2組實驗解求外方位元素；實驗中分別模擬6個和9個虛擬控制點：像點坐標（xv，yv）在像平面內隨機生成，高程Zv在（Z0-100 m，Z0-100 m）中隨機生成，其中Z0為相片覆蓋區內的平均高程，然后按式（2）計算出虛擬控制點的物方平面坐標（Xv，Yv），進而可與控制點一起平差計算。

3）平差過程迭代結束條件設置為3個角元素改正數都小于0．03'。

2.2 使用9個控制點進行實驗

1）首先測試純控制點解外方位元素，按公式（14）、（15）及ri=（QVVPll）ii分別計算每個點上的粗差發現下限、可控性數值、多余觀測分量，結果如表1（單位權中誤差為0．003 9 mm，迭代次數為3）。

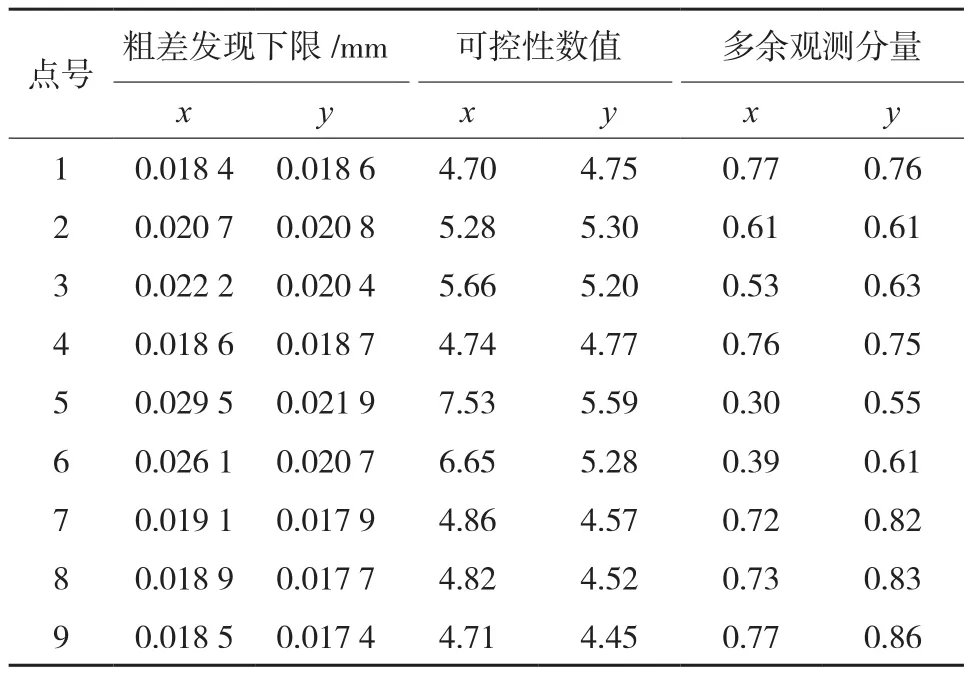
表1 無虛擬點時每個點位上可靠性指標

2）引入9個虛擬控制點整體平差解求，進行了20次實驗，每次虛擬點的像平面坐標及Z坐標隨機生成，因此每次虛擬點3個坐標都不同，平差的網形也不同。計算中控制點、虛擬控制點權分別設置為Pc=1，Pv=1/10，可靠性指標的統計結果如表2（平均單位權中誤差為0．002 5 mm，平均迭代次數為3．3）。

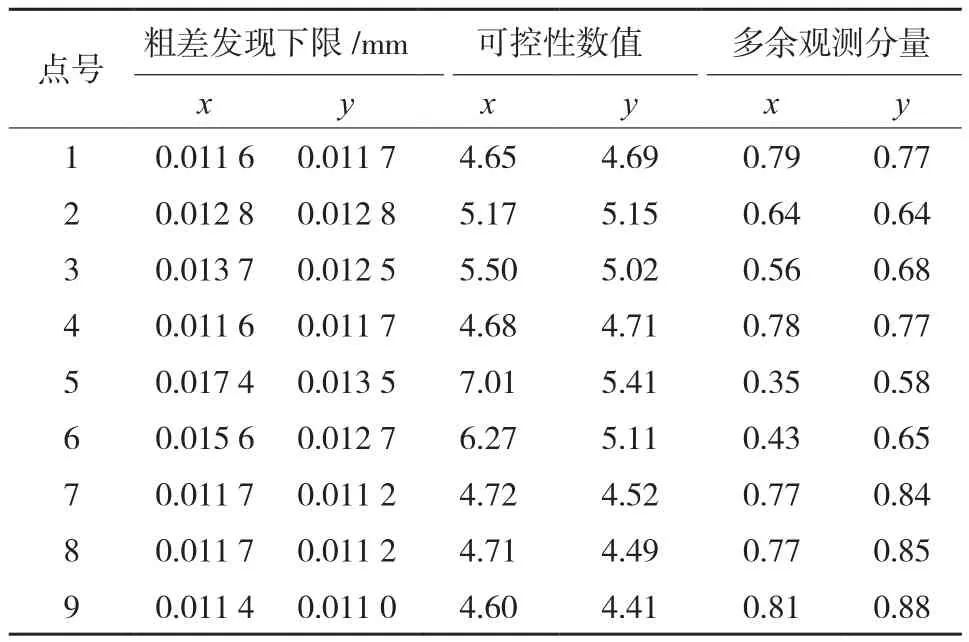
表2 加入虛擬點后每個點位上可靠性指標

3）在純控制點解算未知數情況下，將確定大小的粗差C，分18次加入到9個點共18個坐標觀測值中，即第1次對第1個點的x加入粗差后解算，第2次對第1個點的y加入粗差，第3次對第2個點的x加入粗差，以此類推，直至第18次對第9個點的y加入粗差，保證每次觀測值中只有一個粗差，在解算過程中使用數據探測法進行粗差探測。表3為引入0．04 mm（4．5個像素）粗差所統計的標準化殘差。

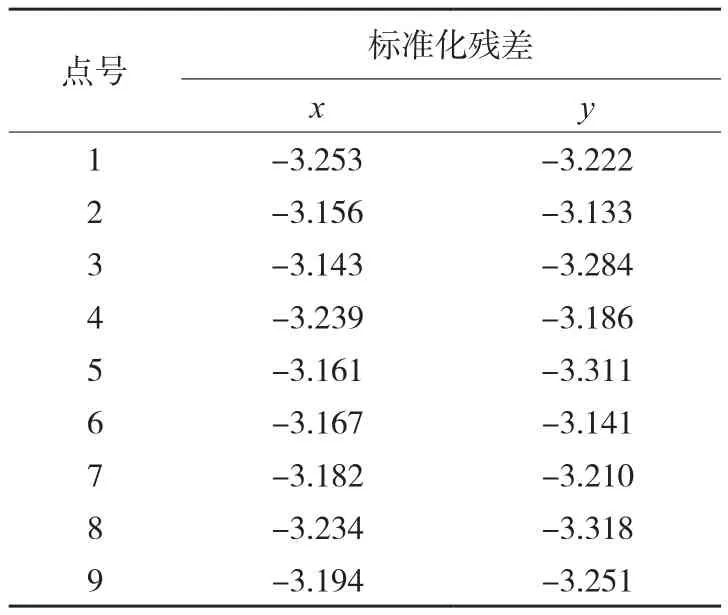
表3 無虛擬控制點的標準化殘差

4）在同時使用虛擬控制點和控制點求解的情況下，同樣對9個控制點的xi、yi分18次加入一定大小的粗差。表4是在2種求解方式下，加入不同大小的粗差，能檢測到粗差的次數，表5為引入0．04 mm粗差（4．5個像素）所統計的標準化殘差。

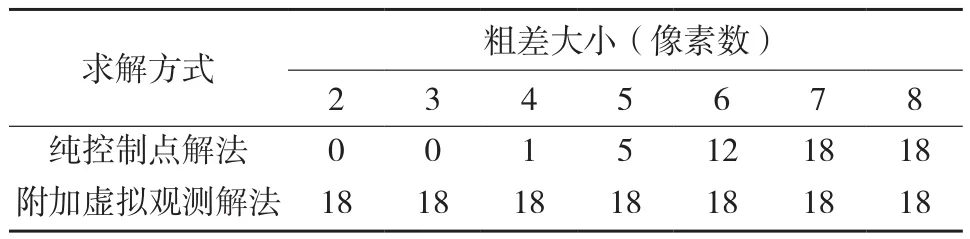
表4 粗差探測統計表

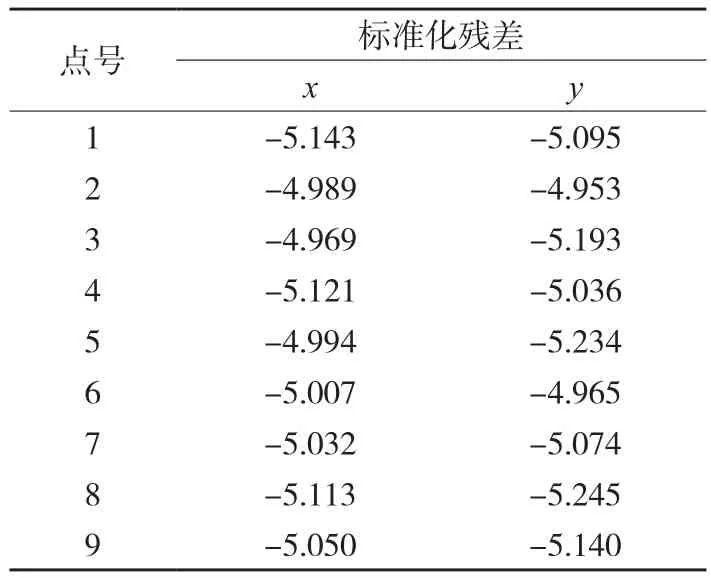
表5 有虛擬控制點的標準化殘差

從表1～5可以看出：

1）給定顯著行水平σ0和校驗功效β0，實驗中σ0=0.1%，β0=80%，非中心化參數δ0=4.13。加入虛擬控制點后，每個控制點的多余觀測分量適量增加，可控性數值降低，粗差檢測的下限降低。

2）令標準化殘差的閾值為Ka=3.29，對于一定大小的粗差（本次實驗中為2～6個像素粗差），加入虛擬控制點后的檢測效率明顯好于只使用控制點。2.3 使用6個控制點進行實驗

如果只使用地面控制點平差，單位權中誤差為0．002 6 mm，迭代次數為3，進行20次隨機模擬虛擬控制點，每次模擬6個，和地面控制點整體平差，平均單位權中誤差為0．001 5 mm，平均迭代次數為3．58次。具體的可靠性指標統計見表6、表7。

表6 無虛擬點時每個點位上可靠性指標

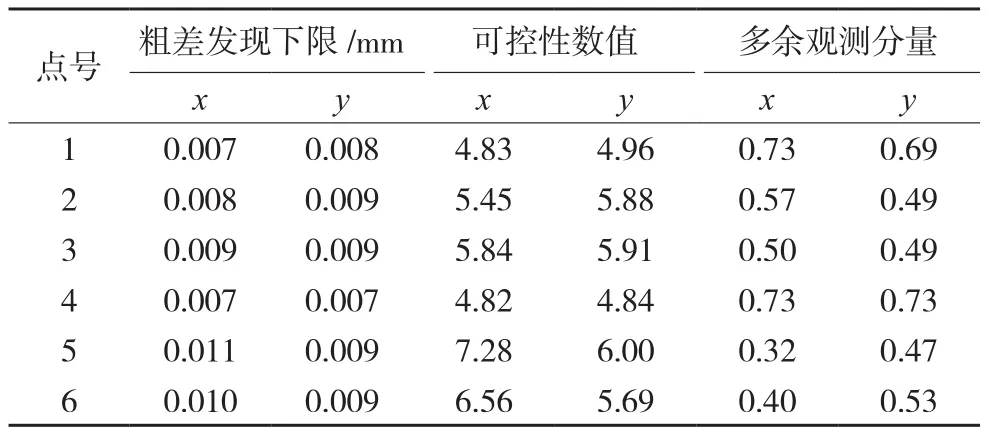
表7 加入虛擬點后每個點位上可靠性指標

對于不加虛擬控制點的情況，每次對每個點的x或y坐標加入0．9 mm（100個像素）的粗差，統計結果如表8；加入虛擬控制點后，加入0．09 mm（10個像素）的粗差，統計結果如表9。

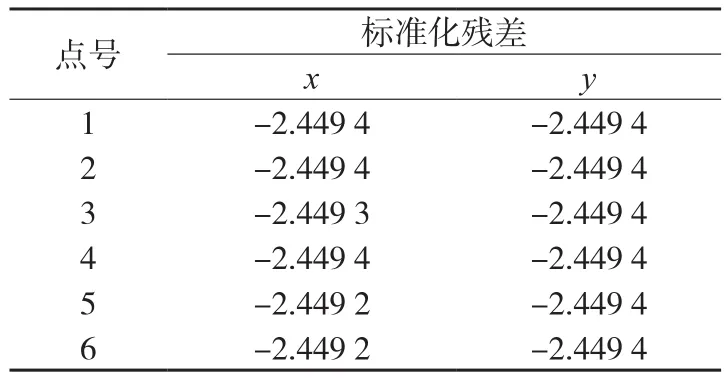
表8 無虛擬控制點的標準化殘差

表9 有虛擬控制點的標準化殘差

由以上結果可知：

1）在一定的圖形條件和觀測精度下，多余觀測過少，使用數據探測法探測粗差是失效的；

2）加入虛擬控制點后，雖然每個點上的多余觀測分量無明顯增加，但使得粗差可以探測，同時也說明了Baarda的可靠性理論與數據探測并不是統一的[2]。

6點法、9點法點位分布圖分別如圖2、圖3所示。

圖2 6點法點位分布圖

圖3 9點法點位分布圖

3 結 語

在已設計好的網形中，對模型誤差只存在粗差的情況，粗差的可發現下界是確定的。如果在平差過程中加入虛擬控制點，降低了粗差可發現下界閾，提高了數據探測法效率，并在一定條件下探測出使用數據探測法不可探測的粗差，提高了后方交會的內部可靠性。

[1] Pelzer H． Some Criteria for the Accuracy and Reliability of Networks[J]． DGK,1980,25(2):55-67

[2] Baarda W． A Testing Procedure for Use in Geodesy Net Works [J]．Neth． Geod． Publ． on Geodesy,1968 ,2(5):23-31

[3] 陶本藻,姚宜斌．可靠性分析與數據探測[J]．武漢大學學報:信息科學版,2002,27(6):607-609

[4] 陶本藻,姚宜斌,施闖．基于相關分析的粗差可區分性[J]．武漢大學學報:信息科學版,2004,29(10):881-883

[5] 施闖,劉經南．基于相關分析的粗差理論[J]．武漢測繪科技大學學報,1998,23(1):5-9

[6] 於宗儔,李明峰．多維粗差的同時定位與定值[J]．武漢測繪科技大學學報,1996,21(4):323-329

[7] 李德仁,袁修孝．誤差處理與可靠性理論[M]．武漢:武漢大學出版社,2005

P207

B

1672-4623（2016）02-0088-04

10.3969/j.issn.1672-4623.2016.02.030

吳磊，工程師，研究方向為航空攝影測量與遙感影像處理。

2015-04-03。