初中“幾何變換”的內容與考法的剖析

周春意

摘要：隨著教育教學改革的深入發展，現代數學思想也隨之不斷滲透，幾何變換以運動變換的觀點研究幾何問題，體現了“形”與“數”的知識融合，把復雜性問題轉化為簡單性的問題而得到解決，逐漸成為中考考查熱點、重點。它的數學思想已越來越引起人們的重視和關注。明確“幾何變換”的內容本質特點及中考測試點，有利于提高教學與復習效率。

關鍵詞：初中數學；“幾何變換”；內容與考法

中圖分類號：G633.6 文獻標識碼：A 文章編號：1992-7711（2016）07-0093

隨著教育教學改革的深入發展，現代數學思想也隨之不斷滲透，幾何變換以運動變換的觀點研究幾何問題，體現了“形”與“數”的知識融合，把復雜性問題轉化為簡單性的問題而得到解決，逐漸成為中考考查熱點、重點，它的數學思想已越來越引起人們的重視和關注。明確“幾何變換”的內容本質特點及中考測試點，有利于提高教學與復習效率。

一、內容剖析

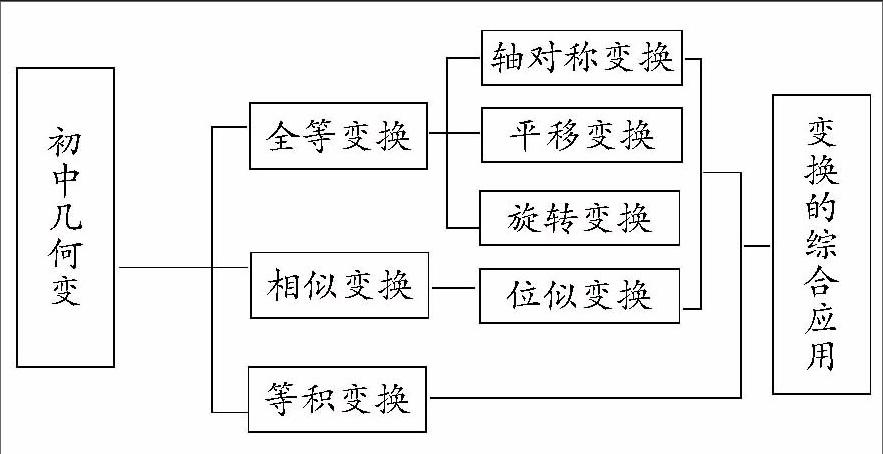
1. 知識結構

2. 知識要點

全等變換問題（軸對稱、平移、旋轉）全等變換：是指不改變圖形形狀與大小的變換。

首先要理解運用這種變換的一些基本情況：

（1）按指令語言，按規定的變換移動圖形；

（2）按指令語言拼接圖形；

（3）根據題目的需要設計變換（需要理解變換的條件與相應的方式與方法；需要解讀好題目的直接或隱含的條件）。

相似變換問題。位似變換：是指不改變圖形形狀只改變圖形大小的變換。

由于相似的知識不是建立在以平行線為依據的前提下，所以我們對圖形的認識是建立在位似變換的基礎之上的，即從位似化為相似，也就是說需要先從相似的角度認識問題.從新課標的角度講相似問題的知識只是要求為基本認識，純推理的問題相對困難，所以我們對這部分知識的定位是以數量計算為主要對象的。

等積變換問題。等積變換：是指不改變圖形大小只改變圖形形狀的變換。

這是新課標在重視幾何變換的前提下與實際問題相結合而形成的問題，它主要體現在以下問題中：①圖形在不改變大小的情況下的移動；②圖形的分割與組合；③圖形的拼接。

3. 主要思想方法

軸對稱你變換：軸對稱是平面到自身的變換，若存在一條定直線l，使對于平面上的每一點P及其對應點P′，其連線PP′都被定直線l垂直平分，則稱這種變換為軸對稱變換，定直線l稱為對稱軸。軸對稱變換有如下性質：（1）把圖形變為與之全等的圖形；（2）關于l對稱的兩點連線被l垂直平分。

證題過程中使用翻折變換，可保留原有圖形的性質，且使原來分散條件相對集中，以利于問題的解決。

平移變換：平移變換是平面到自身的變換，將平面上任一點P變換到P′，使得：（1）射線PP′有給定的方向；（2）線段PP′有給定的長度，則稱這種變換為平移變換。在平移變換下，圖形變為與之全等的圖形，直線變為與之平行的直線。

在解幾何問題時，常利用平移變換使分散的條件集中在一起，具有更緊湊的位置關系或變換成更簡單的基本圖形。

下面是一些常用到的平移變換的特殊情形：（1）與定長、定向的線段有關的問題，常作平移；（2）與梯形、正方形有關的問題，常可利用梯形、正方形的特性作平移。

旋轉變換：旋轉變換是平面到它自身的變換，使原點O變換到它自身，其他任何點X變到X′，使得：（1）OX′=OX；（2）∠XOX′=θ（定角），則稱這樣的變換為旋轉變換，O稱為旋轉中心 。旋轉變換保持圖形全等，但圖形方位可能有變化。在幾何解題中，旋轉的作用是使原有圖形的性質得以保持，但改變其位置，使能組合成新的有利論證的圖形。

在運用旋轉變換解幾何題時，注意下面一些特殊情形：

（1）與等腰三角形有關的問題，常取頂角的頂點為旋轉中心，作旋轉變換；

（2）與正三角形（或正方形）有關的問題，常可利用正三角形（或正方形）的特性作旋轉變換；

（3）與圓有關的問題，常取圓心為旋轉中心作旋轉變換。

當圖形中存在（或適當添加輔助線之后存在）等線段、特別角、全等形、正多邊形等情況時，常常可以試探作一個有用的旋轉變換，使得這個變換帶來新的全等形、相等的線段、相等的角等，從而將巳知條件相對集中，以利于問題的解決。

位似變換：位似變換是兩個圖形不但相似，且每組對應點所在的直線都經過同一點，那么這就是位似圖形。（初中數學中考中暫不命題）

等積變換：等積變換是指在解某些幾何問題時，通過幾何圖形的面積相等，相互間進行轉換，從而使問題得到解決。

4. 重點與難點

幾何變換的重點：了解圖形軸對稱變換、平移變換、旋轉變換、相似變換的概念；會按要求作出簡單平面圖形經軸對稱變換、平移變換、旋轉變換、相似變換后所得的像；理解軸對稱變換、平移變換、旋轉變換的性質：均不改變原圖形的形狀和大小；了解圖形相似變換的性質；通過對圖形變換的欣賞和探索，使學生體會圖形變換在現實生活的存在，激發學生的數學學習興趣，增強審美觀念，培養學生的科學探究精神。

幾何變換的難點：平移變換得根據所提供的平移方向和移動的距離兩個條件作圖；旋轉變換得根據旋轉中心、旋轉的方向和角度三個條件作圖，“以局部帶整體”的作圖思想方法，進一步發展學生的空間觀念；能利用軸對稱、平移、旋轉等方法繪制精美的圖案。

二、考法剖析

幾何變換以運動變換的觀點研究幾何問題，體現了“形”與“數”的知識融合，逐漸成為中考考查熱點、重點，提高了學生運用幾何變換的思想分析、解決問題的能力，它的數學思想已越來越引起人們的重視和關注。

1. 概念性問題——考查學生的基本概念

例1. （2015北京市中考題） 剪紙是我國傳統的民間藝術，下列剪紙作品中，是軸對稱圖形的為（ ）

例2. （2015年哈爾濱市中考題）如圖，在RtABC中，BAC=90°，將ABC繞點A順時針旋轉90°后得到AB′C′（點B的對應點是點B′，點C的對應點是點C′），連接C。若CC′B′=32°，則B的大小是（ ）

A . 32° B. 64° C. 77° D. 87°

2. 開放性問題——考查學生的創造能力

例3. 已知每個網格中小正方形的邊長都是1，圖1中的陰影圖案是由三段以格點為圓心，半徑分別為1和2的圓弧圍成。

（1）填空：圖1中陰影部分的面積是 （結果保留π）；

（2）請你在圖2中以圖1為基本圖案，借助軸對稱、平移或旋轉設計一個完整的花邊圖案（要求至少含有兩種圖形變換）。

這類開放題不同于在固定條件下研究固定結論，學生可以從日常生活、生產或學習中多角度、多層次、多側面地思考問題，發展學生的求異思維，對于激發學生的學習興趣，發揮學生的主體精神，考查學生的個體很有益處。

3. 應用性問題——考查學生的綜合應用能力

例4. （2015年葫蘆島中考題）如圖，在矩形ABCD中，AD=2，CD=1，連接AC，以對角線AC為邊，按逆時針方向作矩形ABCD的相似矩形AB1C1C，再連接AC1，以對角線AC1為邊作矩形AB1C1C的相似矩形AB2C2C1，…，按此規律繼續下去，則矩形ABnCnCn-1的面積為 。

例5. （2015年慶陽市中考題）在如圖所示的平面直角坐標系中，△OA1B1是邊長為2的等邊三角形，作△B2A2B1與△OA1B1關于點B1成中心對稱，再作△B2A3B3與△B2A2B1關于點B2成中心對稱，如此作下去，則△B2nA2n+1B2n+1（n是正整數）的頂點A2n+1的坐標是（ ）

4. 探究性問題——考查學生的分析能力

例6. （2015年岳陽市中考題）已知直線m∥n，點C是直線m上一點，點D是直線n上一點，CD與直線m、n不垂直，點P為線段CD的中點。

（1）操作發現：直線l⊥m，l⊥n，垂足分別為A、B，當點A與點C重合時（如圖①所示），連接PB，請直接寫出線段PA與PB的數量關系： 。

（2）猜想證明：在圖①的情況下，把直線l向上平移到如圖②的位置，試問（1）中的PA與PB的關系式是否仍然成立？若成立，請證明；若不成立，請說明理由。

（3）延伸探究：在圖②的情況下，把直線l繞點A旋轉，使得∠APB=90°（如圖③所示），若兩平行線m、n之間的距離為2k。求證：PA·PB=k·AB。

這類題型主要通過學生的觀察、分析、探究、猜測、推理、驗證等一系列探究活動，從不同的角度和層次來分析和解決問題，體現了新課程標準下要求教師形成開放性、創新性的教學方式，體現了主體性、反思性和合作性等教學思想，要求學生學會“問題——探究——發現——推廣”。因此，此題注重研究探究性問題，做到合情推理和演繹推理相結合，較好地考查學生的分析能力。