多重邊融合復雜網絡動態演化模型

楊迎輝,李建華,沈迪,南明莉,2,崔瓊

(1.空軍工程大學信息與導航學院,710077,西安;2.中國人民解放軍95881部隊,100095,北京)

?

多重邊融合復雜網絡動態演化模型

楊迎輝1,李建華1,沈迪1,南明莉1,2,崔瓊1

(1.空軍工程大學信息與導航學院,710077,西安;2.中國人民解放軍95881部隊,100095,北京)

針對多個性質不同、相互融合的復雜網絡演化過程時變非均衡,網絡結構層級交織,特點規律難以測度的問題,提出了一個多重邊融合復雜網絡動態演化模型。首先,定義多重邊融合復雜網絡的相關概念,分析融合關系與層級關系的轉化過程,按照節點、邊性質的差異,拆分融合節點和重合邊,將多重邊融合復雜網絡轉化成交織型層級復雜網絡;其次,定義節點的度值飽和度和吸引因子,提出交織型層級復雜網絡的演化算法和局域世界演化模型,討論了4種典型的節點演化情形,運用平均場方法分析了模型演化的度分布規律;最后進行了數值仿真分析,結果表明,演化過程結束后,未達到飽和狀態的節點度值服從指數分布且誤差不超過6%,已達到飽和狀態的節點度值服從其連接容量的分布規律且誤差不超過3%,網絡交織系數與最高的新增節點概率、初始邊數呈正相關性。研究結果驗證了模型的可行性和有效性,為探索多重邊融合復雜網絡演化過程與規律提供了新的思路和方法,在交通網、通信網、社交網等結構與動力學研究方面具有良好的應用前景。

多重邊融合復雜網絡;交織型層級復雜網絡;動態演化;飽和度;吸引因子

隨著現代社會網絡化程度的不斷加劇,復雜網絡已經在政治、經濟、軍事等眾多領域廣泛應用[1-2]。現實生活中包含大量的由多種性質子網絡構成的多重邊融合復雜網絡(MLUCN),例如交通網、通信網、社交網等,存在著1個節點具有多種性質、2個節點之間有多條邊連接的情況。相較單一性質、單邊的復雜網絡,MLUCN中邊與邊之間的性質存在較大差異,節點之間的可達路徑數量更多,網絡的演化過程及規律也更加復雜。

當前,關于網絡演化問題的研究主要集中在模型構建、算法設計、特性分析等方面。文獻[3]引入時滯對網絡進行拆分,建立多重邊復雜網絡動力學模型,并基于Lyapunov理論研究網絡的穩定性;文獻[4]針對SF和ER網絡,研究了隨機攻擊條件下層級網絡間的依存關系和依存強度對系統的作用效果;文獻[5]定義了網絡節點度值飽和度,基于二分網絡建立了一種類局域世界演化模型,并分析了演化統計特性;文獻[6]定義了吸引因子概念,提出了一種吸引因子存在的無尺度網絡演化模型,仿真對比了同等網絡規模下,吸引因子模型與BA模型的度分布情況。

已有成果主要是針對單邊、單一性質的網絡,對具有多重邊和融合節點的復雜網絡研究較少,未能有效區分節點和邊的多種性質差異進行演化建模。因此,本文首先根據性質差異,拆分融合節點和重合邊,將MLUCN轉化成交織型層級復雜網絡(ILCN)進行研究;其次,定義節點的度值飽和度和吸引因子,建立ILCN局域世界動態演化模型,并對度分布規律進行理論推算。最后,通過數值仿真驗證了模型的可行性與有效性。

1 MLUCN模型轉化

1.1 相關概念

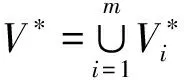
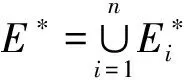
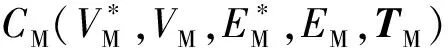
定義4 交織型層級復雜網絡是由部分節點相連,邊性質近似的多個子網組成的具有層級結構、彼此交織的復合網絡[8],記為CC(VC,EC,TC,φC)。其中VC為節點集合,EC為邊集合,TC=(tij)NC×NC為鄰接矩陣,NC=|VC|,φC為網絡交織系數,用于描述子網間交織關系的密切程度[9]。

1.2 融合關系與層級關系轉化

融合關系與層級關系都是對網絡結構進行直觀描述[9],融合關系主要關注網絡的全局屬性,用于分析融合網絡的節點(邊)綜合屬性、可達路徑以及關聯關系,支撐節點等級設置、信息路由規劃等工作。層級關系可較好描述不同子網獨立的拓撲結構,用于分析網絡的分層屬性,支撐子網的任務分配、功能劃分、分層管理等工作[10]。伴隨子網融合程度的改變,融合關系與層級關系可相互轉化。

時的融合關系時的融合關系

時的層級關系時的層級關系圖1 融合關系與層級關系演化示意圖

1.3 拆分運算

在MLUCN中,融合節點的多種性質為其演化中的性質歸屬帶來不便,使新節點在優選時不能準確區分節點性質。重合邊的存在造成多條性質不同的邊在外在形式上統一表現為一條總的邊,使統計已有節點的度值變得較為困難和不準確。在ILCN中各個節點、邊相對獨立,不存在融合、重合的情況,有利于準確探索不同性質子網的演化規律[11]。本文通過拆分運算將MLUCN轉化為ILCN進行研究,根據對象的不同,拆分運算分為融合節點拆分、重合邊拆分和網絡整體拆分。

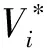
(1)

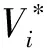
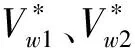
(a)MLUCN (b)ILCN圖2 MLUCN與ILCN轉化過程示意圖

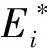
(2)

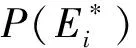
1.3.3 網絡整體拆分 在融合節點、重合邊拆分基礎上,網絡整體可被拆分為多個單一性質的子網,且部分子網可能不為連通網絡。對于CM,網絡整體拆分運算為

(3)

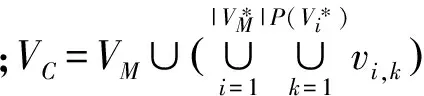
2 ILCN動態演化模型

與BA無標度網絡不同,由于受管理體制、成本、體積等影響,多數現實網絡節點往往具有差異化的連接增長能力,都具有一定的連接容量(連接數量上限),所能連接的節點數是有限的,網絡邊不會無限制增長。為保證網絡具有良好的均衡性和較強的抗毀性[1],新增節點會從飽和度較低的節點集合中擇優連接。同時,網絡中已有節點都具有各自的吸引因子,也會影響新增節點的擇優過程及結果。本文以飽和度作為已有節點成為候選節點的判定準則,以吸引因子作為新增節點優先連接的主要依據,探索構建ILCN動態演化模型。

2.1 節點飽和度與吸引因子

定義5 節點飽和度是節點連接容量與度值之間的分段函數。通過飽和度的限制,可降低網絡演化中節點度值的差異性,使生成的邊相對均勻分布,促進網絡整體的均衡性。在演化時刻t,節點Vi的飽和度函數可表示為

(4)

式中:Ωi為節點Vi的連接容量;ki(t)為節點Vi的度值;k*為節點的度值閾值;Ω*為飽和度的相對穩態值;Θ(Ωi,ki(t))為節點飽和度函數,通常與Ωi的變化趨勢成正比,與ki(t)的變化趨勢成反比。若Ωi相對固定,初始時Bi(t)隨ki(t)的增大而減小,當ki(t)達到閾值k*后,雖然后續仍會不斷增大,但Bi(t)基本不再變化,穩定在Ω*。

選擇節點飽和度作為網絡已有節點是否需要增加邊的衡量標準,并以此被動生成新增節點的動態局域世界[5]。不同類別節點集合中新加入的節點,只能在對應類別、未飽和的節點集中擇優選擇。為便于表述,文中設定節點飽和度函數為Bi(t)=Ωi-ki(t),其中ki(t)∈[0,Ωi]。若Bi(t)=0,即ki(t)=Ωi,表明節點達到了度飽和狀態,不會成為新增節點的候選連接對象。若Bi(t)>0,即ki(t)<Ωi,表明節點會成為局域世界的候選連接對象。

定義6 節點吸引因子是指單位時間內節點獲得的新增邊數量,表示網絡中已存在節點對新增節點的復合吸引變量。對節點Vi,吸引因子可表示為

(5)

式中:Δt為時間間隔;ΔE為節點獲得的新增邊數。

吸引因子的存在對新增節點擇優選擇概率具有較大影響,一個僅有很少連接但具有很高吸引因子的節點,雖然進入網絡的時間不久,也能具有很高的連接速率,并在短時間內獲得大量連接,快速達到度飽和狀態[7]。

2.2 演化模型構造算法

設初始時刻節點連接容量矩陣為Ω=[Ωi]m0×1,其中m0為節點數量。不同性質節點具有各自新增概率,優先與同類節點相連接,只有當同類未飽和節點數量小于新增節點初始連接數時,新增節點才會從其他類別未飽和的節點中根據節點度值和吸引因子進行選擇。當新增節點與被選中節點類型確定后,邊的類型隨之確定。因此,演化過程中不考慮邊的類型及概率,構造算法如下。

(1)開始于較少的節點數m0和連接數e0,每個演化步長內新增1個單一性質節點,性質為S的節點新增概率為pS(0≤pS≤1),并連接到m(m≤m0)個已存在的同類節點上[12]。

(2)根據演化時刻t的網絡中同類節點度值,計算每個同類節點的飽和度,被動生成新增節點的同類型局域世界。

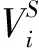
(6)

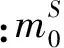
(7)

經過t個演化步長,該算法可產生一個擁有t+m0個節點和mt+e0條邊的網絡。

2.3 節點演化不同情形的討論

受節點飽和度及吸引因子的影響,ILCN演化中節點會分為4種不同的情形,如圖3所示。其中,節點中白色圓孔的數量代表節點固有的連接容量。

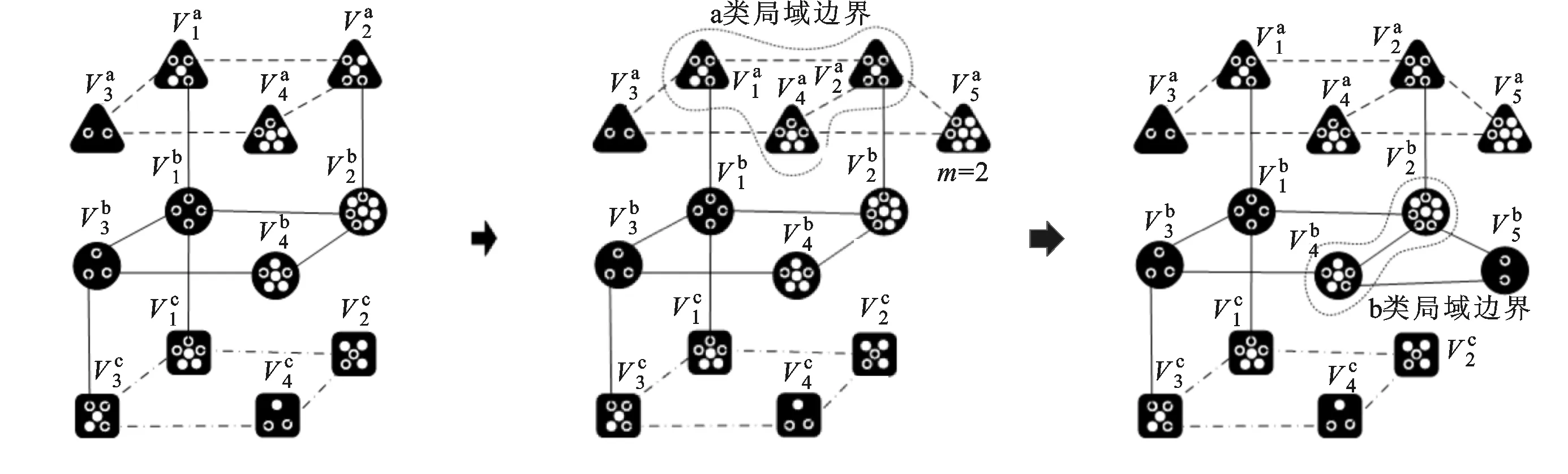
圖3 ILCN演化過程示意圖

當Bi小、Υi大時,此類節點一般會快速與新增節點相連,但受制于飽和容量,當節點度值達到相對飽和的狀態后便保持不變,成為比較穩定的節點,與進入網絡時間的長短無關。

當Bi、Υi小時,此類節點優先連接概率最小,邊的增加十分緩慢,一般都會逐漸演變成為邊緣節點。

2.4 節點度分布分析

受節點連接容量的限制,節點的度分布分為2種極端的情況。

(1)節點連接容量Ωi較大,演化結束后各節點度值均未達到飽和狀態,可用平均場方法分析節點度分布規律。ILCN演化中僅存在優先連接,分析中假設

(8)

(9)

經歷演化時間t后,平均度數為

(10)

(11)

將式(11)代入式(7),可得

(12)

(13)

(14)

新增節點在相同時間間隔內加入網絡,則時間t服從均勻分布,即

(15)

由此可得

(16)

kS(t)的概率密度為

(17)

當t→∞時,節點的度分布為

(18)

ILCN模型的節點度分布服從指數分布規律,通過調節參數m、pS,可使指數在-4～0之間變化。

(2)節點連接容量Ωi較小,演化結束后各節點度值全部達到飽和狀態。節點度值等于連接容量,節點的度分布規律與連接容量的分布規律相一致,可能服從固定分布,也可能是隨機分布。實際中,每個節點的連接容量都是在綜合考慮成本、效益、需求及外在環境等因素的基礎上確定的。

通常,ILCN模型演化介于上述2種極端情況之間,節點的度分布表現為混合分布形式,未達到飽和狀態的節點度分布服從指數分布規律,而已達到飽和狀態的節點度分布服從連接容量的分布規律。

3 仿真實驗分析

圖4 初始MLUCN模型及轉化后的ILCN模型

3.1 MLUCN模型轉化

3.2 m固定,pa、pb、pc變化時的節點度分布

當m=1,pa、pb、pc取不同概率組合時,各類節點的度分布如圖5所示。由圖5可知,對任意一條分布曲線,隨著節點度值k的增加,概率值總體在減小,當k達到一定數值后,概率值便保持相對平穩,呈現典型的指數分布特點。這是因為m較小,新增節點加入網絡后,對已有節點度值的影響較慢,演化結束后,網絡中多數節點仍處于未飽和狀態,僅少數連接容量較小或吸引因子較大的節點達到度飽和狀態。以m=1、pa=0.2、pb=0.3、pc=0.5時節點為例,24個節點中僅3個節點達到度飽和狀態,占總數的12.5%,通過仿真擬合方法確定節點度值服從指數分布,且指數λ=2.773。將參數pb、m代入式(18)中,得到理論計算的指數值為2.6,仿真擬合結果與理論計算值基本一致,僅存在約6%的誤差,驗證了模型中度分布理論推算的正確性。

由圖5可知:當pa=0.2、pb=0.3、pc=0.5時,仿真擬合得到λ=2.773;當pa=0.3、pb=0.4、pc=0.3時,仿真擬合得到λ=2.876,2個概率組合的指數λ結果基本一致,誤差僅為3.6%。由此可得,當m相同時,盡管pa、pb、pc發生了變化,但各類性質節點的度分布曲線變化不大,僅個別度值的概率產生起伏,總體仍服從指數分布,表明在本文模型中新增節點的概率不是影響節點度分布的關鍵因素。

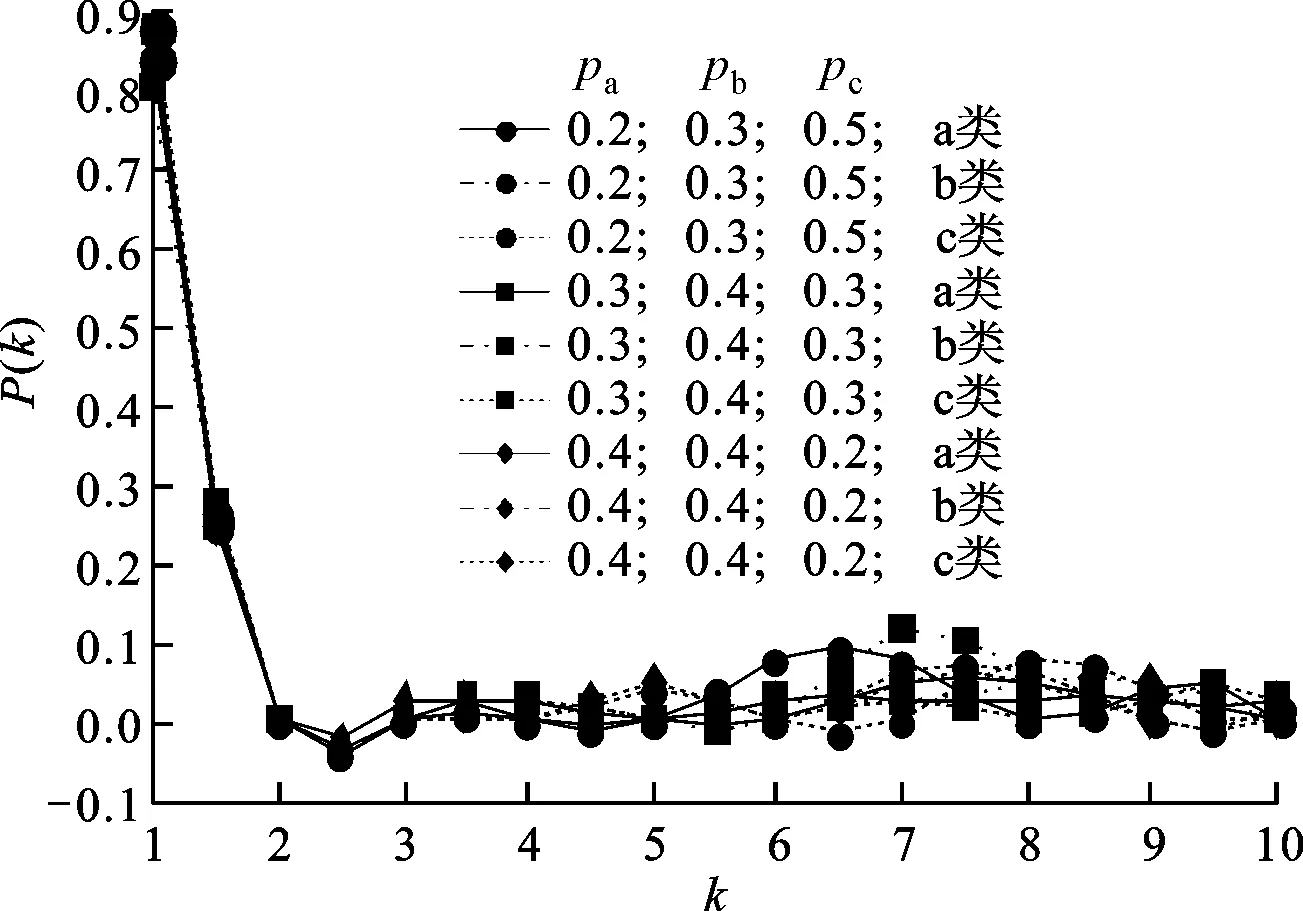
圖5 m=1,pa、pb、pc逐漸改變時節點的度分布

3.3 pa、pb、pc固定,m變化時的節點度分布

當pa=0.2、pb=0.3、pc=0.5,m由1變化至3時,節點度分布如圖6所示。由圖6可知,m=1時3類節點度分布曲線基本服從指數分布,但隨著m增加,初段度值(1～3)的概率大幅下降,中段度值(4～7)的概率明顯提升,末段度值(8～10)的概率基本保持不變,曲線中僅部分區間呈指數分布。這是因為m≥2時新增節點進入網絡的初始邊數在2以上,在隨后的多次演化中節點度值快速增加使低度值節點不斷減少,m越大,低度值衰減越快、出現概率越小。由于演化總步長顯著大于各節點的連接容量,演化結束后大部分節點度值都穩定在連接容量附近,達到度飽和狀態[13]。對已飽和節點的度分布進行擬合,與仿真設置的理論結果基本一致,數學期望誤差約為2%,方差誤差約為3%。當m=2時,對未達到飽和狀態的節點度分布進行仿真擬合,得出指數λ=1.37。將參數pb、m代入式(18)中,得到理論計算的指數值為1.3。由此可知,仿真擬合結果與理論計算值基本一致,僅存在約5%的誤差。

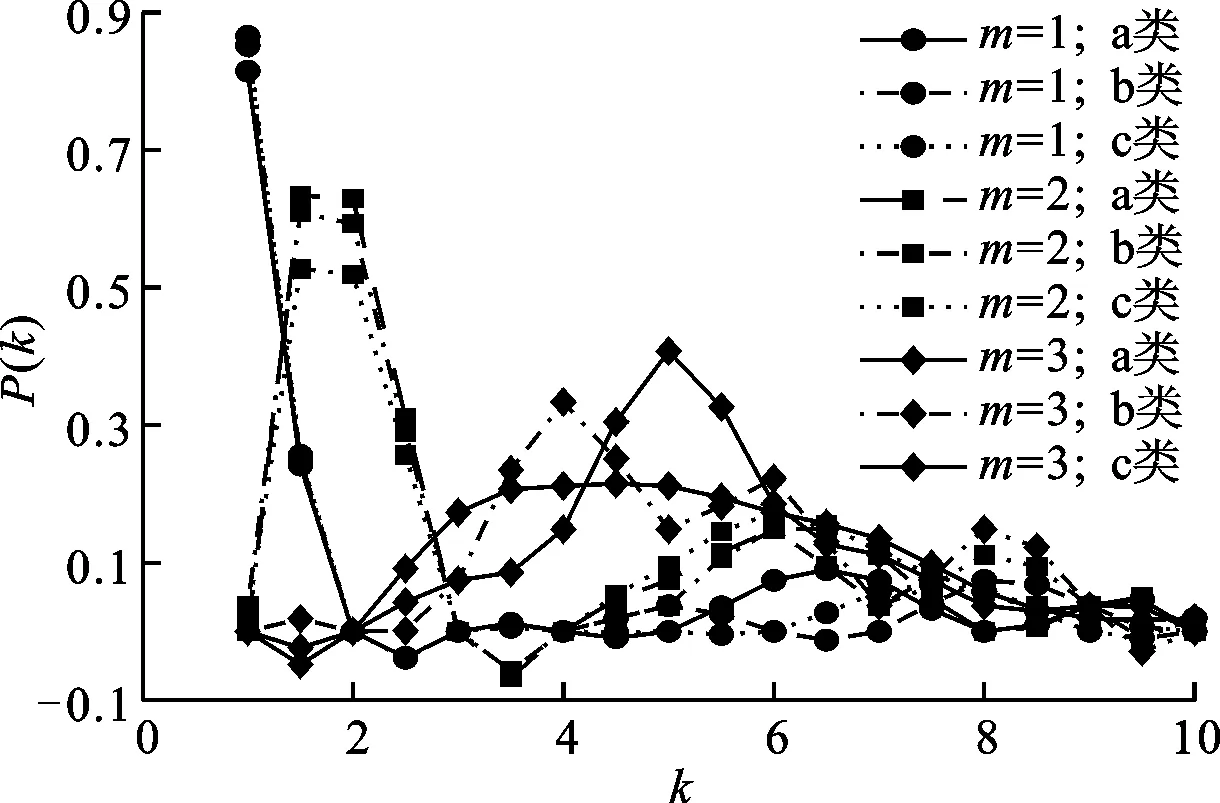
圖6 pa=0.2、pb=0.3、pc=0.5,m逐漸增大時 節點的度分布

3.4 pa、pb、pc及m變化時φc的變化趨勢

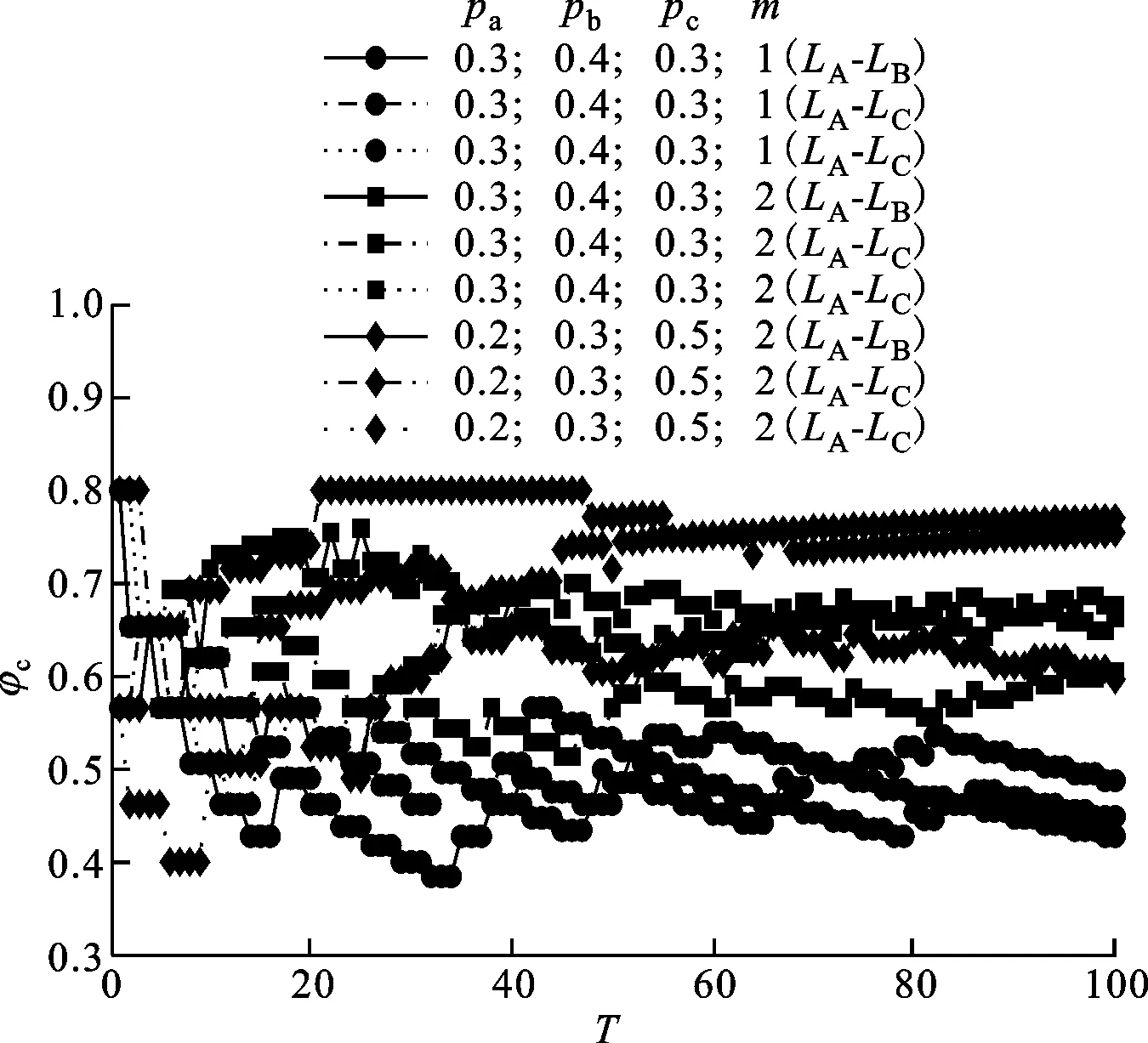
圖7 pa、pb、pc及m變化時φc的變化趨勢

當pa、pb、pc及m分別取2組值時,ILCN的網絡交織系數φc隨演化步長的變化趨勢如圖7所示。由圖7可知,任意2層網絡的交織系數總體上隨演化的推進而呈現階梯式起伏振蕩,最終趨于相對穩定。當pa、pb、pc固定時,m取值越大,φc也相應較大。這是因為較大的m要求新增節點與較多節點建立連接,當同類未飽和節點數量小于m時,新增節點會選擇與其他類別的未飽和節點(屬于其他子網)相連接,增加了網絡之間的交織節點數量,促進了網絡的節點交織程度[14]。

當m固定時,包含新增概率較高類別節點的φc較大。這是因為c類節點的概率值最高,節點新增數量最多,優先連接機理會使LC中節點的度值普遍較大且增速較快,甚至有部分節點提前達到度飽和狀態。為滿足連接數量要求,新增節點會從其他類別的未飽和節點中擇優建立連接,從而增加了不同類別節點之間的交織邊數量,使網絡間的邊交織關系更加密集、更加復雜。

4 結 論

本文針對多個性質不同、相互融合的復雜網絡演化問題,探索建立了一種基于節點飽和度和吸引因子的動態演化模型,并仿真分析了節點度分布及網絡交織系數的變化情況,有以下主要結論。

(1)在節點度值飽和度和吸引因子的共同作用下,網絡全部節點的度值服從混合分布規律,即未達到飽和狀態的節點度值服從指數分布,已達到飽和狀態的節點度值服從其連接容量的分布規律;混合分布的參數取值與m密切相關,但與新增節點的類型概率相關性不強。

(2)網絡交織系數與最高的新增節點概率、m呈正相關性,隨著演化步長的逐步推進,發生階梯式起伏振蕩,并最終趨于相對穩定。

[1] CASTET J F, SALEH J H. Interdependent multi-layer networks: modeling and survivability analysis with applications to space-based networks [J]. PLOS ONE, 2013, 8(4): e60402.

[2] WANG Zhen, SZOLNOKI A, PERC M. Self-organization towards optimally interdependent networks by means of coevolution [J]. New Journal of Physics, 2014, 16: 033041.

[3] 高洋, 李麗香, 彭海朋, 等. 多重邊復雜網絡系統的穩定性分析 [J]. 物理學報, 2008, 57(3): 1444-1451. GAO Yang, LI Lixiang, PENG Haipeng, et al. Stability analysis of complex networks with multi-links [J]. Acta Phys Sin, 2008, 57(3): 1444-1451.

[4] JIANG J, LI W, CAI X. The effect of interdependence on the percolation of interdependent networks [J]. Physica: A Statistical Mechanics and Its Applications, 2014, 410: 573-581.

[5] 田立新, 賀瑩環, 黃益. 一種新型二分網絡類局域世界演化模型 [J]. 物理學報, 2012, 61(22): 228903. TIAN Lixin, HE Yinghuan, HUANG Yi. A novel local-world-like evolving bipartite network model [J]. Acta Physica Sinica, 2012, 61(22): 228903.

[6] 陶少華, 趙會洋, 平源, 等. 基于吸引因子的無尺度網絡演化模型研究 [J]. 復雜系統與復雜性科學, 2008, 5(2): 88-92. TAO Shaohua, ZHAO Huiyang, PING Yuan, et al. Attractive factors based scale-free networks evolving model [J]. Complex Systems and Complexity Science, 2008, 5(2): 88-92.

[7] AOKI T, YAWATA K, AOYAGI T. Self-organization of complex networks as a dynamical system [J]. Physical Review: E, 2015, 91(1): 012908.

[8] STIPPINGER M. Enhancing resilience of interdependent networks by healing [J]. Physica: A Statistical Mechanics and Its Applications, 2014, 416: 481-487.

[9] 沈迪, 李建華, 張強, 等. 交織型層級復雜網 [J]. 物理學報, 2014, 63(19): 190201. SHEN Di, LI Jianhua, ZHANG Qiang, et al. Interlacing layered complex networks [J]. Acta Physica Sinica, 2014, 63(19): 190-201.

[10]SANTOS M D, DOROGOVTSEV S N, MENDES J F. Biased imitation in coupled evolutionary games in interdependent networks[R/OL]. [2015-12-26]. http: ∥www.nature.com/articles/srep04436?message -global=remove&WT.ec_id=SREP-639-20140325.

[11]邵峰晶, 孫仁誠, 李淑靜, 等. 多子網復合復雜網絡及其運算研究 [J]. 復雜系統與復雜性科學, 2012, 9(4): 20-25. SHAO Fengjing, SUN Rencheng, LI Shujing, et al. Research of multi-subnet composited complex network and its operation [J]. Complex Systems and Complexity Science, 2012, 9(4): 20-25.

[12]孫欽東, 孫亞紅, 管曉宏, 等. 動態短信通信復雜網絡演化模型研究 [J]. 西安交通大學學報, 2009, 43(6): 5-9. SUN Qindong, SUN Yahong, GUAN Xiaohong, et al. A dynamic evolution model of short message complex network [J]. Journal of Xi’an Jiao Tong University, 2009, 43(6): 5-9.

[13]WANG Baokui, PEI Zhenhua, WANG Long. Evolutionary dynamics of cooperation on interdependent networks with the Prisoner’s Dilemma and snowdrift game [J]. EPL, 2014, 107(5): 58006.

[14]向海濤, 梁世東. 雙復雜網絡間的演化博弈 [J]. 物理學報, 2015, 64(1): 018902. XIANG Haitao, LIANG Shidong. Evolutionary gambling dynamic for two growing complex networks [J].

Acta Physica Sinica, 2015, 64(1): 018902.

[本刊相關文獻鏈接]

戴啟華,劉勤讓,沈劍良,等.采用集簇方法的片上網絡動態映射算法.2016,50(8):52-58.[doi:10.7652/xjtuxb201608 009]

孫澤宇,伍衛國,曹仰杰,等.無線傳感器網絡中能量均衡參數可控覆蓋算法.2016,50(8):77-83.[doi:10.7652/xjtuxb 201608013]

趙皓,高智勇,高建民,等.一種采用相空間重構的多源數據融合方法.2016,50(8):84-89.[doi:10.7652/xjtuxb201608 014]

徐張寶,馬大為,姚建勇,等.采用干擾估計的液壓系統自適應魯棒控制.2016,50(8):123-129.[doi:10.7652/xjtuxb2016 08020]

魏倩,蔡遠利.一種基于神經網絡的中制導改進算法.2016,50(7):125-130.[doi:10.7652/xjtuxb201607019]

張小棟,郭晉,李睿,等.表情驅動下腦電信號的建模仿真及分類識別.2016,50(6):1-8.[doi:10.7652/xjtuxb201606001]

姜濤,黃偉,王安麟.多路閥閥芯節流槽拓撲結構組合的神經網絡模型.2016,50(6):36-41.[doi:10.7652/xjtuxb201606 006]

劉兆麗,秦濤,管曉宏,等.采用用戶名相似度傳播模型的線上用戶身份屬性關聯方法.2016,50(4):1-6.[doi:10.7652/xjtuxb201604001]

陳斌,胡平舸,屈丹.子空間域相關特征變換與融合的語音識別方法.2016,50(4):60-67.[doi:10.7652/xjtuxb201604010]

王富平,水鵬朗.采用多尺度方向微分比率的角點檢測算法.2016,50(4):68-75.[doi:10.7652/xjtuxb201604011]

賀王鵬,訾艷陽,陳彬強.沖擊特征受控極小化通用稀疏表示及其在機械故障診斷中的應用.2016,50(4):94-99.[doi:10.7652/xjtuxb201604015]

丁建坤,韓德強,楊藝.最短特征線段多分類器系統設計.2015,49(9):77-83.[doi:10.7652/xjtuxb201509014]

周遠,周玉生,劉權,等.一種適用于圖像拼接的DSIFT算法研究.2015,49(9):84-90.[doi:10.7652/xjtuxb201509015]

孫忱,奚宏生,高榮.鄰域線性最小二乘擬合的推薦支持度模型.2015,49(6):77-83.[doi:10.7652/xjtuxb201506013]

朱愛斌,胡浩強,何大勇,等.采用頻域融合方法的砂輪刀具磨損三維重構技術.2015,49(5):82-86.[doi:10.7652/xjtuxb201505013]

謝文軍,付曉,于振華,等.信息物理融合系統中惡意軟件傳播動力學研究.2015,49(4):78-83.[doi:10.7652/xjtuxb 201504013]

徐田華,楊連報,胡紅利,等.高速鐵路信號系統異構數據融合和智能維護決策.2015,49(1):72-78.[doi:10.7652/xjtuxb201501012]

(編輯 趙煒)

Dynamic Evolution Model of United Complex Networks with Multi-Links

YANG Yinghui1,LI Jianhua1,SHEN Di1,NAN Mingli1,2,CUI Qiong1

(1. Information and Navigation Institute, Air Force Engineering University, Xi’an 710077, China; 2. The Unit 95881 of PLA, Beijing 100095, China)

Aiming at the problem that during the evolution process of interconnected complex networks, there exist nonuniform time-varying property and layered interlaced network structure, leading to the difficulty in measuring their characteristics and rules, a dynamic evolution model of united complex network with multi-links (MLUCN) is proposed. Firstly, we define some related concepts of MLUCN, analyze the conversion process of fusion and hierarchy relationship, and split fusion nodes and overlapped edges according to the property difference between nodes and edges, then the MLUCN is transformed to interlaced layered complex networks (ILCN). Secondly, the node degree saturation and attraction factor are defined. The evolution algorithm and local-world evolution model for ILCN are put forward, and four situations of node evolution are discussed. The mean field method is used to analyze the degree distribution rule during evolution. Finally, numerical simulation is performed. The results show that the node degree not reaching saturation obeys the exponential distribution with an error no more than 6%; the node degree reaching saturation obeys their connection capacities’ distribution with an error no more than 3%; the network weaving coefficients have a positive correlation with the highest probability of new node and the initial number of connected edges. The results verified the feasibility and effectiveness of the proposed model. This model provides a new idea and method for exploring MLUCN evolution process and rule, and also has good application prospects in the structure and dynamics researches of transportation network, communication network and social network, etc.

united complex network with multi-links; interlaced layered complex network; dynamic evolution; saturation; attraction factor

2016-01-18。 作者簡介:楊迎輝(1988—),男,博士生;李建華(通信作者),男,教授。 基金項目:國家自然科學基金資助項目(61573017,61401499,61174162)。

10.7652/xjtuxb201609021

N94

A

0253-987X(2016)09-0132-08