多目標車輛路徑問題的粒子群優化算法研究

郭森,秦貴和,2,張晉東,于赫,盧政宇,于佳欣

(1.吉林大學計算機科學與技術學院,130012,長春;2.吉林大學符號計算與知識工程教育部重點實驗室,130012,長春;3.吉林大學軟件學院,130012,長春)

?

多目標車輛路徑問題的粒子群優化算法研究

郭森1,秦貴和1,2,張晉東1,于赫1,盧政宇1,于佳欣3

(1.吉林大學計算機科學與技術學院,130012,長春;2.吉林大學符號計算與知識工程教育部重點實驗室,130012,長春;3.吉林大學軟件學院,130012,長春)

針對粒子群算法(PSO)及其變種在約束多目標等復雜問題優化過程中所遇到的易陷入局部最優和收斂性問題,提出了一種基于動態學習和突變因子的粒子群算法(DSPSO)。首先,通過分析粒子群群體的學習機制,采用動態的學習策略,使粒子自適應動態調整認知成分和社會成分在迭代更新中的權重,以引導自身向最優解的方向探索,有效改善了群體的收斂速度;其次,通過引入階梯突變因子的概念,使粒子在陷入局部最優時進行試探跳躍,階梯突變賦予粒子突破更新步長限制的能力,使粒子在當前位置速度矢量方向上的二維空間鄰域內進行試探尋優,當發現更優解時則跳出當前局部最優;最后,通過在BenchMark基準函數測試集中典型函數上的實驗,證明了DSPSO的求解精度和收斂速度均優于對比算法。在多目標車輛路徑問題實例優化中,解的可接受率和成功率分別為0.91和0.66,遠優于對比算法中最優解的0.16和0.11,體現了所提改進算法在車輛路徑問題中的優越性。

車輛路徑問題;多目標優化;粒子群

基于群體行為的群體智能算法由于在多向性和全局性等層面的優越性,使其對Pareto非支配解集前沿的形狀和連續性相對不敏感,是目前應用研究較為理想的隨機優化策略。基于隨機優化技術的遺傳算法、蟻群算法等多目標優化算法[1-2]和結合粒子群算法、神經網絡等機制的融合算法[3-5],在約束多目標求解Pareto最優解集中取得了良好的效果。

粒子群算法是1995年由Kennedy等提出的啟發式方法,最初用來解決連續解空間上的優化問題。隨后,提出了基于離散空間的粒子群優化算法(BPSO),并應用于0-1規劃的離散問題上[6]。文獻[7]對連續PSO直接離散化,在更新過程中進行近似取整,將改進的BPSO應用于高維整數規劃問題,得到了穩定性較高的解,且很少產生陷入搜索停滯的情形。文獻[8]將PSO應用于多目標旅行商(MOTSP)問題中,文獻[9]將PSO用于車輛路徑問題(VRP)的優化中,均取得了良好的優化結果。此外,粒子群算法在約束優化、動態優化、多目標優化等領域[10-11]都取得了廣泛的研究與應用,但是粒子群及其變種算法在解決復雜問題時普遍具有收斂性和易陷入局部最優的問題。

車輛路徑問題是典型的組合優化問題,考慮距離、時間和費用成本等多目標約束條件下的車輛路徑優化,是一種類多峰問題。本文從分析粒子群算法本身的學習機制入手,通過動態學習方式進行種群的迭代更新,讓粒子自適應調整更新過程中認知成分和社會成分的比重,并采用突變機制賦予粒子突破更新步長限制的能力,以跳出局部最優解。文中選取其他5種改進的粒子群算法作對比,并通過BenchMark基準測試函數和多目標的有容量限制的車輛調度問題(CVRP)驗證了本文改進算法的有效性。

1 標準PSO算法

經典標準PSO算法[12]中,粒子群中的粒子迭代更新公式為

(1)

式中:ω為經典線性模型;pid和pgd分別為粒子群中個體局部最優和全局最優位置;c1、c2為學習因子常量;r1、r2為兩個0與1之間的隨機數;c1r1(pid-xid)、c2r2(pgd-xid)分別為粒子更新過程中的認知成分和社會成分,c1r1、c2r2決定著每個個體對個體最優和全局最優的信任程度。當c1r1較大時粒子更加信任個體極值,受個體極值的影響較大,將會更多的向個體極值靠近,此時有利于粒子在局部尋優,提高開發能力;反之,當c2r2較大時粒子會更加信任當前全局最優值,受全局最優值影響較大,粒子將會向全局最優值移動,有利于粒子全局尋優過程的進行,增強其探索能力,同時有利于算法的收斂。

2 改進PSO算法及VRP問題模型

2.1 改進的PSO算法

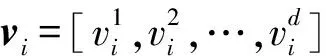
(2)

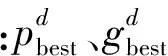
(3)

θ0∈[0,1]為一常數,當隨機數φ大于Pb時,適當降低社會成分在速度更新中的比重,此時粒子受個體極值的引導較大,反之則減少認知成分在速度更新中的比重,粒子更多向全局最優值學習。Pb的處理機制為[14]

(4)

式中:T、t分別為種群最大迭代次數和當前迭代次數,在迭代初期對學習概率影響較大,使得粒子更傾向于向全局最優學習,使群體較快收斂,迭代對學習概率的影響逐漸減小,粒子更多向個體極值學習,這有利于種群多樣性的保持;fit(xi)為當前解xi的適應度計算函數;h1為粒子當前位置適應度與全局最優位置適應度的近似程度;h2為迭代次數的改變對學習概率的影響;m、n分別取值為0.15和0.30[13]。

本文采用BenchMark基準函數測試集中的典型函數來測試常量θ0的最優取值區間,選取Sphere、Rosenbrock兩個單峰函數及Restrigin、Schwefel兩個多峰函數,將學習因子常量θ0在區間[0,1]中均勻取11組值,分別執行100次,得到4個測試函數上的平均運行結果,如圖1所示。

(a)Sphere函數 (b)Rosenbrock函數

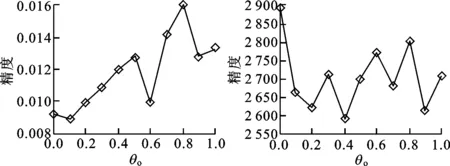
(c)Griewank函數 (d)Schwefel函數圖1 動態學習因子常量在測試函數中的運行結果

2.1.2 避免陷入局部最優解的輔助機制 由粒子群算法的優化機制可知,粒子在進行一步更新后,當且僅當此次更新后所得解優于個體極值,該解才能被采納,成為新的個體最優值,否則該解對整個種群的進化無效,粒子將在原個體極值基礎上重新進行一步更新。當粒子陷入局部最優時,以當前的更新步長難以發現該局部最優解以外的全局最優解。

本文采用階梯突變的機制,引入突變因子σ,賦予粒子突破當前更新機制限制的能力。當群體陷入局部最優時,通過調整粒子的更新步長和前進方向,讓粒子在當前個體最優解速度矢量方向上進行階梯試探。本文采用調整權重因子的方法實現該突變機制,當發現種群陷入局部最優時,在當前迭代數的基礎上調整權重因子w的大小,即

ω=ω±kσ,k=1,2,3,…,n

(5)

式中:σ為突變因子,采用線性慣性權重模型[12]在當前迭代數下的單步步長;k為突變階梯;n為階梯上限。當粒子陷入局部最優時,突變階梯k從1開始取值進行突變,此時權重因子分別進行一次正向和反向的突變,并進行一次更新過程,若一次突變后仍不能發現更優解,則增大突變階梯值,此時權重因子將隨之產生更大幅度的突變,粒子將會跳向原本正常更新機制中所不可能行進到的位置進行尋優,若在某次突變過程中發現比當前最優解更好的解,停止突變,粒子則跳出當前局部最優位置,行進到該突變位置處繼續尋優過程。若突變階梯值達到上限值n后仍不能跳出當前局部最優值,終止該突變操作,還原權重因子到突變前的狀態,將突變階梯值k取為1,繼續先前迭代過程至迭代數上限,結束該尋優過程。

2.2 多目標的車輛路徑問題

多目標優化問題可描述為

(6)

式中:x為決策變量;y為目標向量;M為約束條件集合所決定的可行解域。

車輛路徑問題是指通過配送中心調度,為一系列配送點配送貨物,通過合理安排配送路線,達到最優配送的目的,問題描述如下。

有一個配送中心站,配備有K輛配送車,裝載容量為hk(k=1,2,…,K),有L個配送點要求配送貨物,各配送點的貨物需求量為ei(i=1,2,…,L),且maxei≤maxhk,求滿足需求的最優配送路線。

車輛路徑問題(VRP)比多旅行商(MTSP)問題[14]的約束條件嚴格,求解復雜,且具有實際意義。最優配送是指配送路線的最優化如距離最短等,本文采用多目標模型來處理車輛路徑問題,考慮車輛配送路線中的距離最短、時間最短和費用最少3個目標,各目標距離、時間、費用的計算公式為

(7)

(8)

(9)

式中:i為車輛編號;Sei為車輛i在配送任務中的總路程;j為兩個配送點間路段的編號;H為路段總數;Leij為i車路線中的j路段長度;Tei為完成i車路線所需的時間;Veij為i車j路段上的平均行駛速度;weij為i車j路段單位距離的收費標準;u為單位距離耗油費用。

本文建立的多目標函數模型為

miny=f(x)={g1(x),g2(x),g3(x)}

(10)

g1(x)=S;g2(x)=T;g3(x)=Q

(11)

為盡可能減少算法計算量以降低算法的復雜度,在計算最終配送路線的優化程度時,采用如下權重模型[15]統一各目標值量綱

(12)

式中:G為配送路線的最終近似度;gi(x)*為第i個目標在單目標約束下最優配送路線的理想值;ωi為單目標所占比重;N為目標總數。G越高,配送路線就越理想。求解DSPSO算法的多目標車輛路徑問題fit(x)=G(x),則可得求解過程如下。

開始

2. 初次計算各粒子的適應度;

3. 計算pbest、gbest并確定多目標最終相似度G;

4. loop

5. 計算學習概率Pb;

6. 確定動態學習因子對<θ1,θ2>;

8. 計算各粒子的適應度;

9. 更新各粒子的pbest及最終相似度G′;

10. ifG′>G

11. 更新全局最優解gbest并更新G,G=G′;

12. else ifG=G′

13. Forj=1 ton

14. 進行一次階梯突變,更新w,重新計算G′;

15. ifG′>G

16. 更新pbest、gbest、G,G=G′

17. 還原w到突變前的值,終止突變;

18. end if

19. 如果迭代次數達最大迭代數,跳出循環;

20. end loop

結束

3 實驗結果與分析

3.1 Benchmark測試函數

為了檢驗本文算法的有效性,采用Benchmark基準函數測試集中的典型函數進行測試,選取4個單峰問題函數和4個多峰問題函數,如表1所示。實驗環境為:AMD Athlon處理器,主頻2.70 GHz,2.0 GB內存,Win7環境下搭建Microsoft VS 2013。

實驗中ω采用文獻[12]的經典線性模型,遞變區間為[0.4,0.9],粒子個體數為40,函數維數為30,動態學習因子常量取值0.2,最大迭代數為10 000,并選取帶慣性權重的粒子群算法PSO-w[16]、標準PSO算法SPSO[12]、帶收斂因子的PSO算法PSO-x[17]、組合學習策略PSO算法CPSO[13]、平均最優信息的PSO算法[18]AVGPSO 5種粒子群變體算法進行測試比較。此5種算法與本文改進算法參數設置一致,每個算法在每一基準函數上分別運行60次,統計各算法在各基準函數上運行的最優值(BR)、標準差(SD)、達到可接受解的成功次數(SN)及成功率(SR)等,如表2所示。

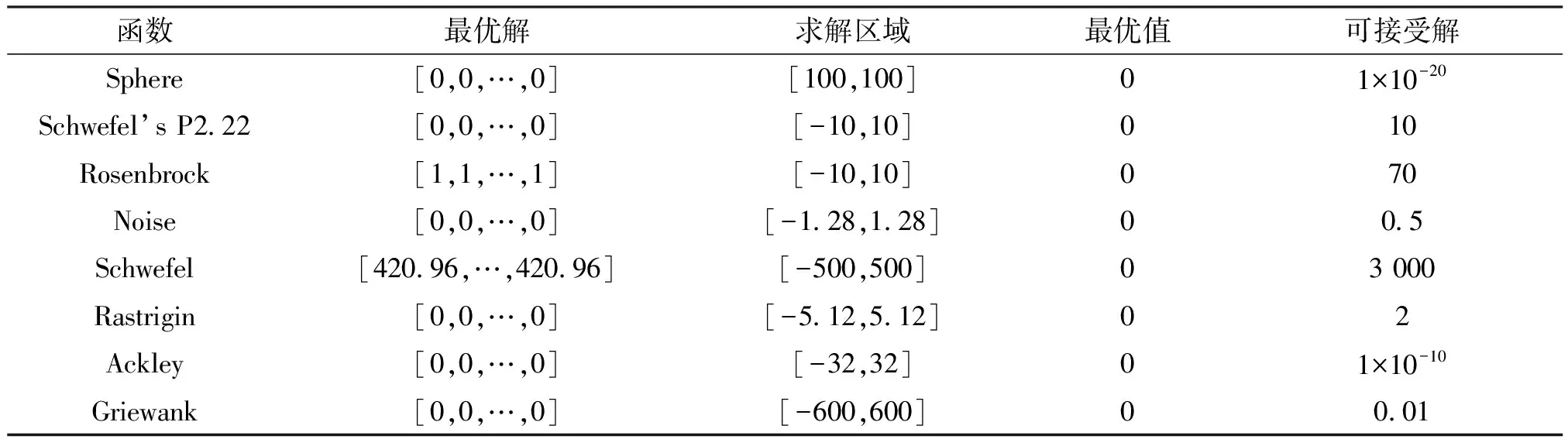
表1 8個維度為30的Benchmark基準測試函數

表2 6種對比算法在Benchmark測試函數上的運行結果

由表2可得,單峰函數中Noise函數由于其持續的擾動特性,本文算法無法獲得較為理想的解。AVGPSO算法在迭代初期開始就引入平均信息,而本文算法的動態學習引導是一個逐漸調整的過程,調整較緩慢,故在相同迭代數下AVGPSO優于本文算法。在求解精度和穩定性上,本文算法明顯優于其他對比算法。

為了檢驗各算法的特性,本文采用迭代數來反映各算法的收斂性,避免由于編程技巧的不同而對收斂時所用CPU時間產生的影響,對單峰函數采集各算法在測試函數上每迭代200次后的優化值,最大迭代數為4 000,多峰函數每500次迭代采集一次優化結果,最大迭代次數為10 000,根據執行60次的平均結果數據,在MATLAB上進行擬合,收斂性對比如圖2、3所示。

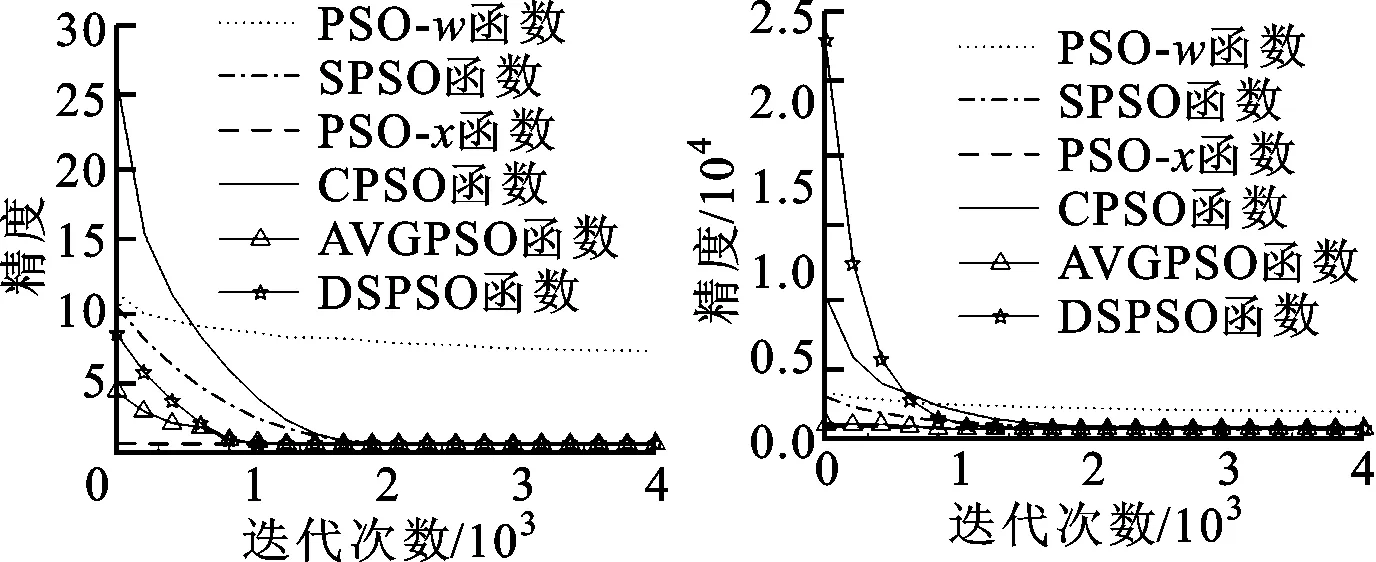
(a)Sphere函數 (b)Rosenbrock函數

(c)Schwefel P2.22函數 (d)Noise函數圖2 4個單峰函數上各對比算法的收斂性對比

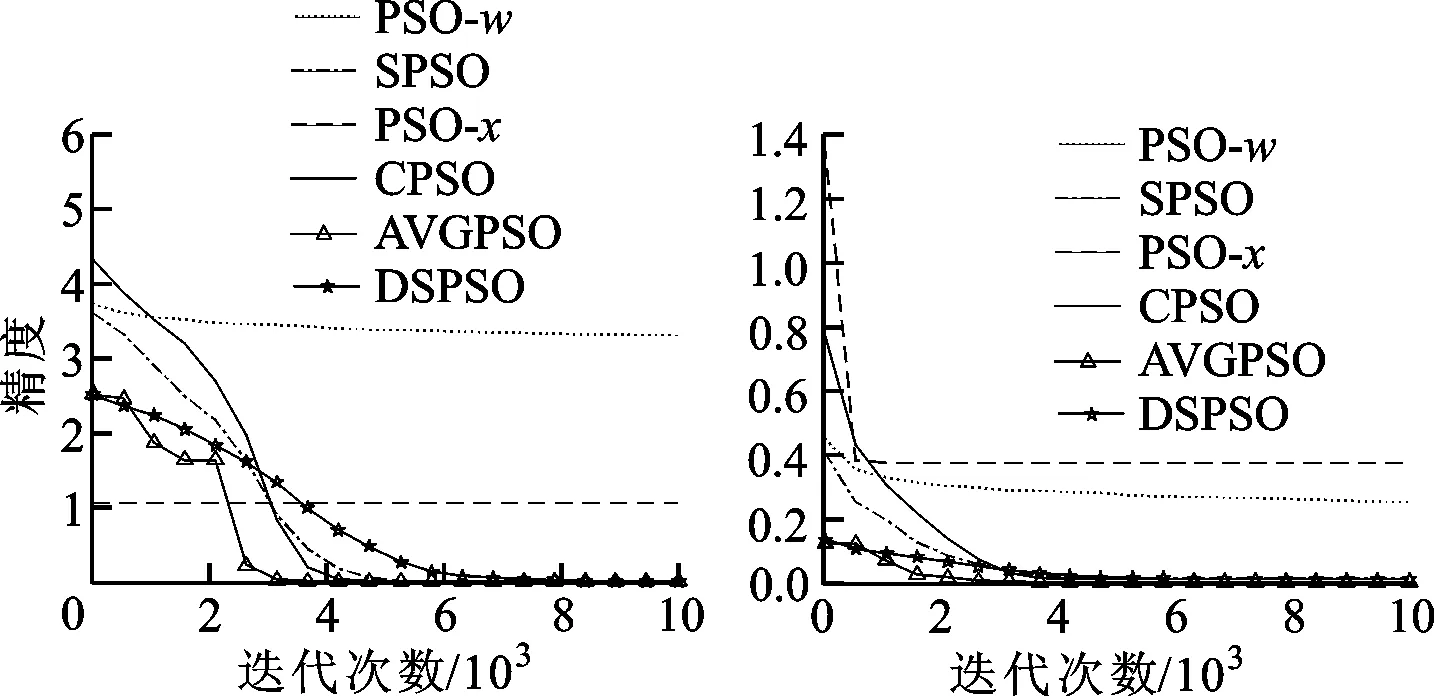
(a)Ackley函數 (b)Griewank函數

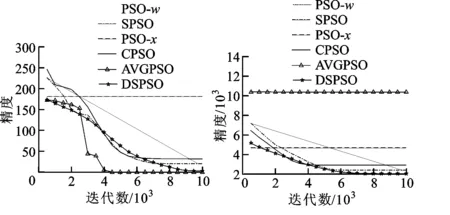
(c)Rastrigin函數 (d)Schwefle函數圖3 4個多峰函數上各對比算法的收斂性對比

由圖2、3可知,單峰函數中極值點處即為最優解。相比其他對比算法,本文算法中采用的自適應引導能夠使粒子在較少迭代數內求得更好的最優解,即使粒子群體更快速收斂到極值點。多峰函數具有多個極值點,過快的收斂會因為早熟而使粒子陷入局部最優或者跳過全局最優位置,本文突變機制有效增加了種群的多樣性,防止種群陷入局部最優而失去全局探索能力,在保證種群收斂的前提下能探索獲得更好的全局最優解。

3.2 車輛調度實例驗證

為了驗證本文改進算法在多目標車輛路徑問題上的處理能力,本文選取VRP數據庫中的E-n22-k4實例,該實例共有22個配送點,一個為配送中心(編號1),其余為待配送點,各點坐標位置及配送需求如表3所示。

借鑒文獻[9]的編碼機制,車輛調度的多目標選取為距離S、時間T和費用Q0。為了簡化問題,假定任兩個配送點間為單一路段,并用該兩點間的歐氏距離代表該路段的長度,得距離矩陣S0。根據表5中各個配送點位置坐標,為了盡可能模擬任意路段本身及其各種屬性的多變性和不確定性,本文采用生成隨機對稱矩陣V0、W0和U0的方式,矩陣分別代表S0中各路段上的平均行駛速度、道路收費和油耗費用,通過式(7)、(8)、(9)、(12)計算配送路線中的各單目標值和最終近似度。

實驗中慣性權重ω采用文獻[12]的經典線性權重模型,動態學習因子常量取值0.2,種群大小為60,迭代數為200,配送車輛K=4,單車限載容量為6 000,使用本文算法對各單目標進行多車單目標優化,如圖4所示。

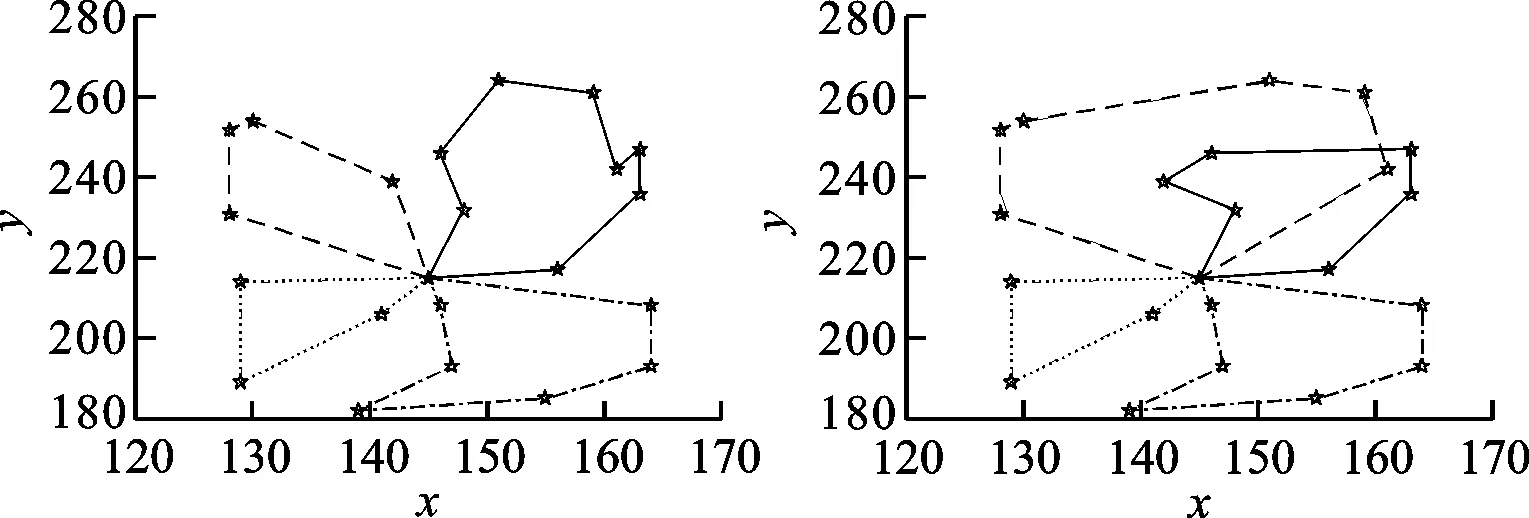
(a)無容量車載軌跡圖 (b)有容量車載軌跡圖

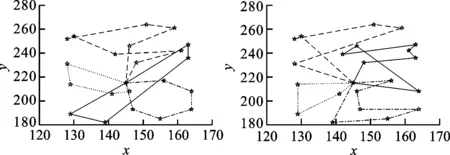
(c)時間最短軌跡圖 (d)費用最少軌跡圖圖4 單目標優化最優路徑軌跡圖

各單目標最優值及最優配送路線如下。

距離S:394.433

車1路線:1→12→5→4→2→3→8→1

車2路線:1→17→20→14→1

車3路線:1→13→10→6→7→9→11→1

車4路線:1→16→19→21→22→18→15→1

表3 各配送點坐標位置及配送需求

時間T:5.702

車1路線:1→6→7→2→3→8→10→15→1

車2路線:1→16→19→21→22→18→1

車3路線:1→17→20→14→1

車4路線:1→4→5→9→12→11→13→1

費用Q:356.271

車1路線:1→13→15→18→19→21→22→1

車2路線:1→17→20→14→1

車3路線:1→12→3→2→5→4→1

車4路線:1→16→7→9→6→8→10→11→1

上述單目標最優值為多目標優化時的各單目標理想值,對比5種變種粒子群算法與本文改進算法在多目標優化實例上的效果。實驗中粒子群種群大小為60,迭代數為200,配送車輛數為4,單車載容量為6 000,每個算法分別運行70次,將相似度大于0.5的優化結果稱為可接受解,大于0.6為成功解。分別計算各算法獲得可接受解與成功解的次數及最優解,可接受率/成功率記為R1/R2,最優相似度記為S,最優相似度解對應的各單目標值(距離/時間/費用)記為B,結果如表4所示。

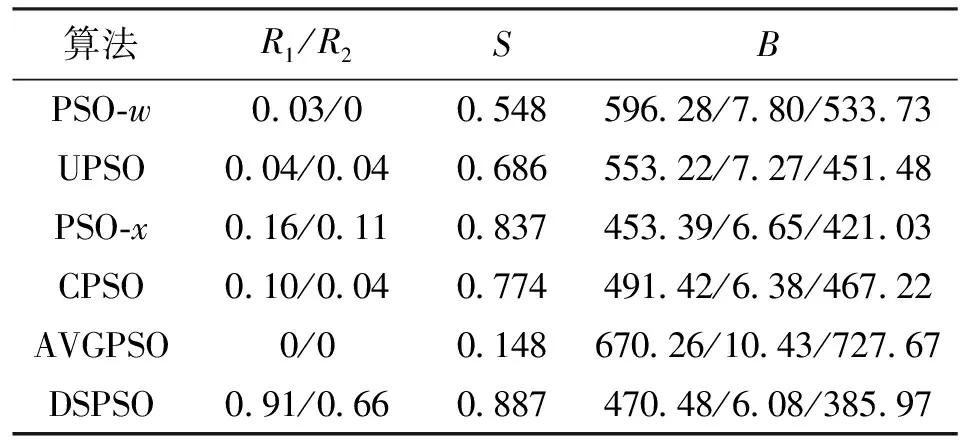
表4 各對比算法在實例上的運行結果對比

本文改進算法最優配送路線如下。

車1路線:1→4→5→9→7→2→3→8→15→1

車2路線:1→12→14→20→22→1

車3路線:1→6→10→11→16→13→1

車4路線:1→18→21→19→17→1

在相同實驗環境下,各參數設置:粒子種群大小為60,迭代數為100,配送車輛數為4,車載容量為6 000。將5種對比算法及本文改進算法DSPSO分別在該實例上運行400次,采集每次運行所得最終近似度,如圖5～7所示。

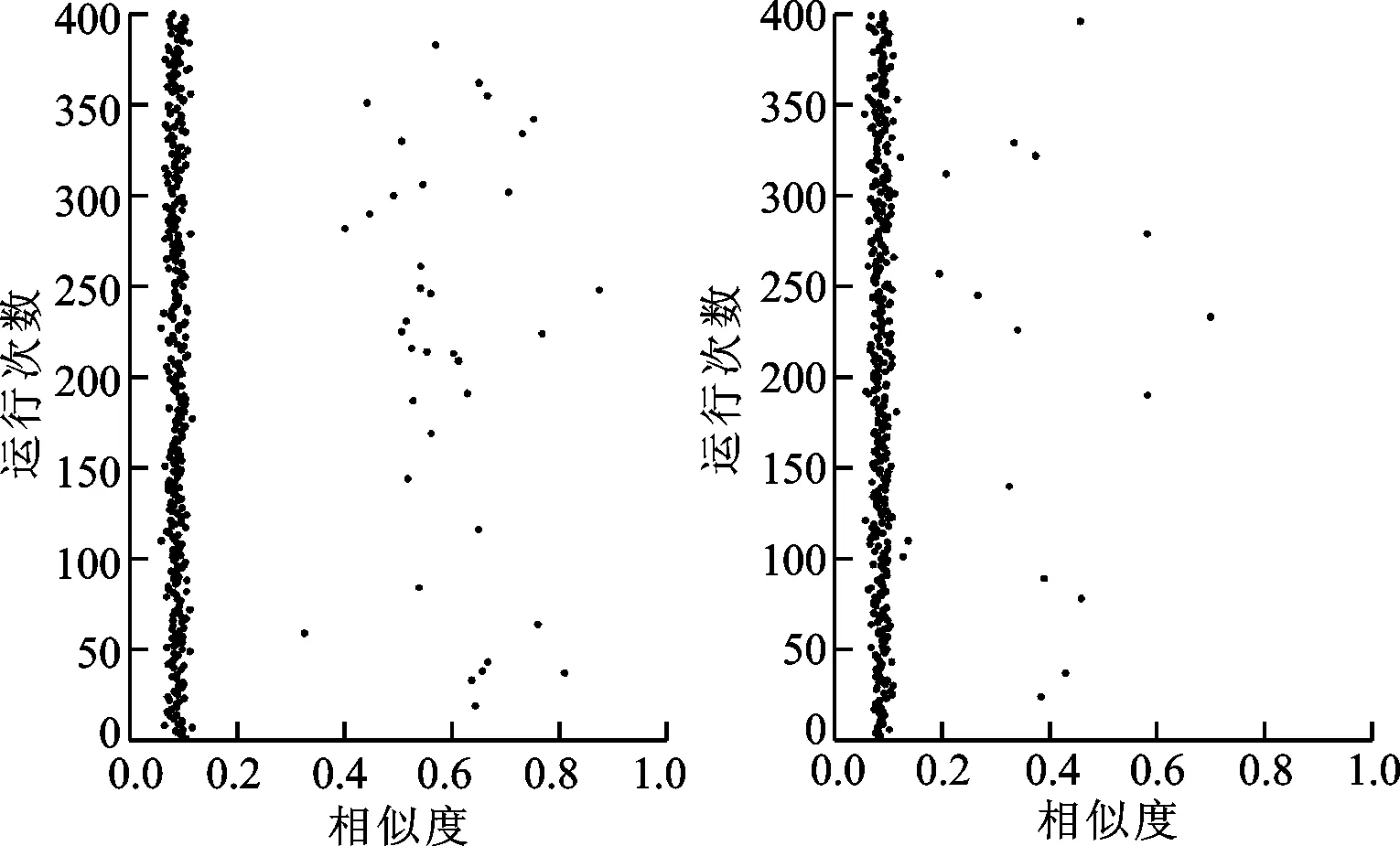
(a)PSO-w運行結果 (b)SPSO運行結果圖5 PSO-w和SPSO對比算法運行結果

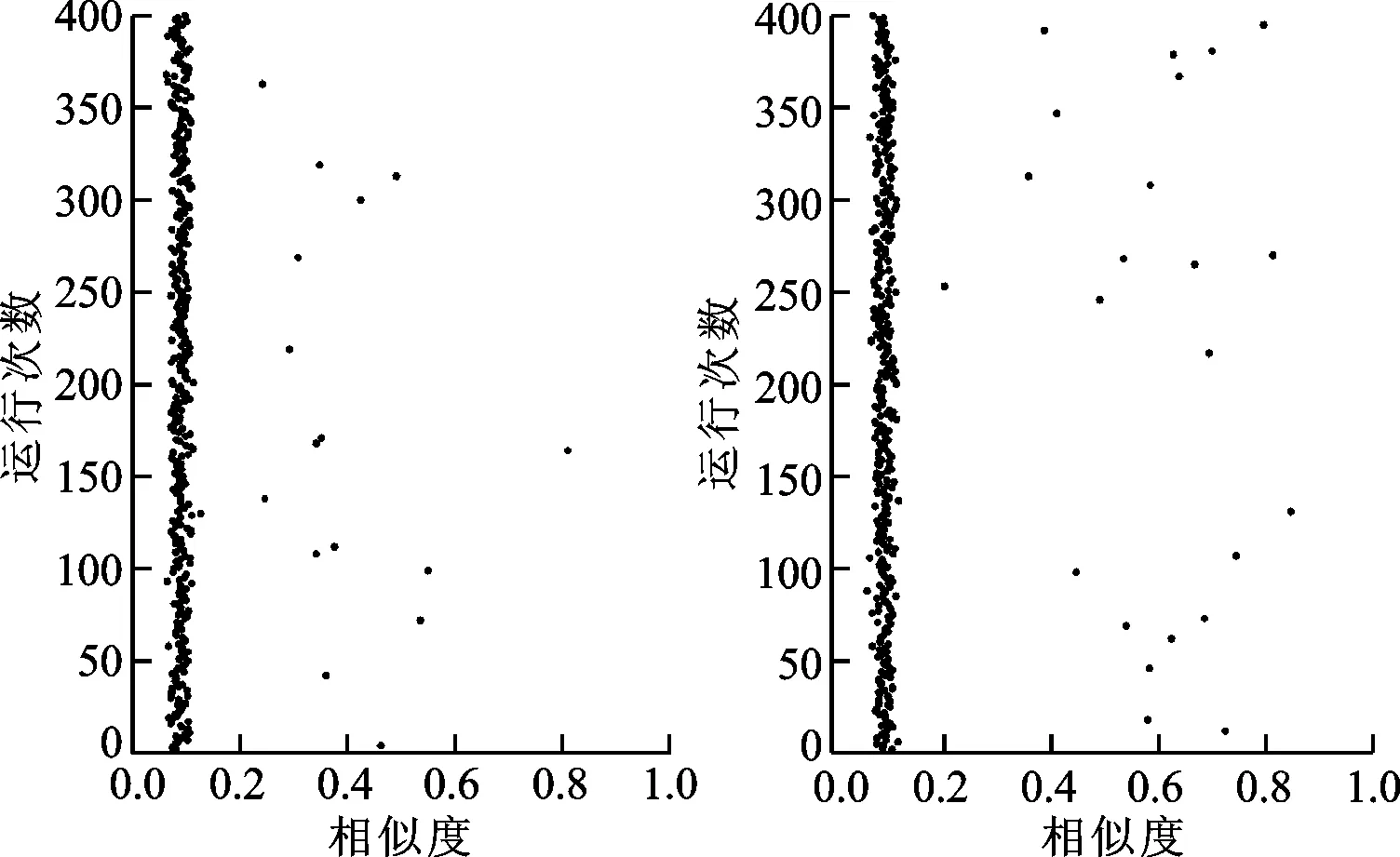
(a)PSO-x運行結果 (b)CPSO運行結果圖6 PSO-x和CPSO對比算法運行結果

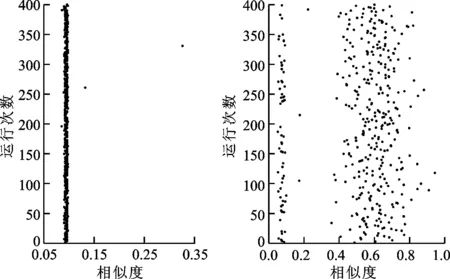
(a)AVGPSO運行結果 (b)DSPSO運行結果圖7 AVGPSO和DSPSO的運行結果

由表4可得,本文改進算法在可接受率和成功率上優于其他對比算法,且最優相似度也遠優于其他對比算法。對比圖5～7可得,5種對比算法相似度聚集在0.1,而本文改進算法則較多分布在[0.45,0.85]區間內,說明本文改進算法在多目標優化問題中更接近真實Pareto邊界,體現了在多目標優化問題上的有效性。

4 結 論

針對粒子群及其變種算法易陷入局部最優和收斂性問題,本文提出基于動態學習策略的粒子群算法。將優化過程中的迭代數和粒子個體極值與全局極值的近似度相結合,動態調整社會成分和認知成分在更新時的比重,引導粒子發現更優解,有效改善了種群的收斂性。同時,引入階梯突變因子,賦予粒子突破當前更新步長的能力,有效避免粒子陷入局部最優,增強全局尋優的能力。

通過Benchmark基準測試函數集中的典型單峰和多峰函數測試,結果表明本文改進算法較其他對比算法有更好的求解精度和穩定性,且可在保證收斂的前提下調節算法的收斂速度。多目標車輛路徑問題的實驗表明,本文算法較其他對比算法能夠獲得更優的配送路線,體現了在CVRP優化問題上的良好性能。

[1] YUSUF I, BABA M S, IKSAN N. Applied genetic algorithm for solving rich VRP [J]. Applied Artificial Intelligence, 2014, 28(10): 957-991.

[2] ZHANG Changsheng, YIN Hao, ZHANG Bin. A novel ant colony optimization algorithm for large scale QoS-based service selection problem [J]. Discrete Dynamics in Nature and Society, 2013(6): 1104-1116.

[3] KENNEDY J, EBERHART R C. Particle swarm optimization [M]. Berlin, Germany: Springer, 2010: 760-766.

[4] CHATTERJEE S, SARKAR S, HORE S, et al. Particle swarm optimization trained neural network for structural failure prediction of multistoried RC buildings[M/OL]∥Neural Computing & Applications. [2015-12-12]. http: ∥link. springer. com/article/10.1007/s00521-016-2190-2.

[5] 許榕, 周東, 蔣士正, 等. 自適應粒子群神經網絡交通流預測模型 [J]. 西安交通大學學報, 2015, 49(10): 103-108. XU Rong, ZHOU Dong, JIANG Shizheng, et al. A traffic forecasting model using adaptive particle swarm optimization trained neural network [J]. Journal of Xi’an Jiaotong University, 2015, 49(10): 103-108.

[6] KENNEDY J, EBERHART R C. A discrete binary version of the particle swarm algorithm [C]∥IEEE International Conference on Systems, Man, and Cybernetics. Piscataway, NJ, USA: IEEE, 1997: 4104-4108.

[7] PARSOPOULOS K E, VRAHATIS M N. Recent approaches to global optimization problems through particle swarm optimization [J]. Natural Computing, 2002, 1(2): 235-306.

[8] WANG Zutong, GUO Jiansheng, ZHENG Mingfa, et al. Uncertain multiobjective traveling salesman problem [J]. European Journal of Operational Research, 2015, 241(2): 478-489.

[9] LI Ning, ZOU Tong, SUN Debao. Particle swarm optimization for vehicle routing problem [J]. Journal of Systems Engineering, 2005, 19(6): 596-600.

[10]DUAN Peibo, ZHANG Changsheng, ZHANG Bin. A local stability supported parallel distributed constraint optimization algorithm[J/OL]. The Scientific World Journal. [2015-12-10]. http: ∥www. hindawi. com/journals/tswj/2014/734975/abs/.

[11]YIN Hao, ZHANG Changsheng, ZHANG Bin, et al. A hybrid multi-objective discrete particle swarm optimization algorithm for a SLA-aware service composition problem [J]. Mathematical Problems in Engineering, 2014, 89(1): 112-121.

[12]SHI Yuhui, EBERHART R C. Empirical study of particle swarm optimization [C]∥Proceedings of the 1999 Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 1999: 1945-1950

[13]TAN Guanzheng, BAO Kun, RIMIRU R. A composite particle swarm algorithm for global optimization of multimodal functions [J]. Journal of Central South University, 2014, 21(5): 1871-1880.

[14]LI Jun, SUN Qirui, ZHOU Mengchu, et al. A new multiple traveling salesman problem and its genetic algorithm-based solution [C]∥The 2013 IEEE International Conference on Systems, Man, and Cybernetics. Piscataway, NJ, USA: IEEE, 2013: 627-632.

[15]TANG Yaoping, YU Hong, WANG Wenmu, et al. Application of TSP model based multi-objective in Yongzhou city’s tourist routes [J]. Journal of Central South University of Forestry & Technology, 2011(10): 154-157.

[16]SHI Yuhui, EBERHART R C. A modified particle swarm optimizer [C]∥The IEEE International Conference on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 1998: 69-73.

[17]CLERC M. The swarm and the queen: towards a deterministic and adaptive particle swarm optimization [C]∥Proceedings of the 1999 Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 1999: 1951-1957.

[18]LI Zhuangkuo, MA Yannan, LIU Liang. Particle swarm optimization based on the average optimal information for vehicle routing problem [C]∥The 6th International Symposium on Computational Intelligence and Design. Piscataway, NJ, USA: IEEE, 2013: 51-54.

(編輯 趙煒)

A Novel Particle Swarm Optimization for Multi-Objective Vehicle Routing Problem

GUO Sen1,QIN Guihe1,2,ZHANG Jindong1,YU He1,LU Zhengyu1,YU Jiaxin3

(1. College of Computer Science and Technology, Jilin University, Changchun 130012, China; 2. Symbol Computation and Knowledge Engineer of Ministry of Education, Jilin University, Changchun 130012, China; 3. College of Software, Jilin University, Changchun 130012, China)

Considering the problems that particle swarm optimization (PSO) algorithm and its variants are easily to fall into local optimal solutions and convergence in the optimization process of complex constrained multi-objective problem, a novel PSO based on dynamic learning strategy and mutation factor (DSPSO) is proposed. First, through analyzing the learning mechanism of particle swarm, DSPSO introduces the dynamic learning strategy, enabling particles to adaptively adjust the weights of cognitive component and social component in the iteration renewal process and guide themselves to explore in the optimal direction, hence effectively accelerating the convergence rate. Second, by introducing the ladder mutation factor, when the particles are trapped in a local optimum, they are enabled to break the limit of update-step size to make tentative jumps in the two-dimensional spatial neighborhood of the velocity vector direction. When a better solution is found, the optimal solution would be updated. Finally, experiments are conducted on the typical functions of BenchMark, and the results show that the accuracy and convergence rate of DSPSO are better than the contrast algorithms. In the multi-objective vehicle routing problem optimization, the acceptable and success rates of the DSPSO solutions are 0.91 and 0.66, respectively, far outperform the results of 0.16 and 0.11 by comparison algorithm, reflecting the superiority of DSPSO in the multi-objective vehicle routing problem.

vehicle routing problem; multi-objective optimization; particle swarm optimization

2016-01-01。 作者簡介:郭森(1991—),男,碩士生;秦貴和(通信作者),男,教授,博士生導師。 基金項目:國家自然科學基金資助項目(51205154);吉林省科技發展計劃資助項目(20140520073JH);吉林省重點科技攻關資助項目(2015020434);中央大學基礎研究基金資助項目(JCKY-QKJC14)。

時間:2016-07-14

10.7652/xjtuxb201609016

TP273

A

0253-987X(2016)09-0097-08

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160714.1117.004.html