振動式壓電風能發電裝置的研究
吳 松,張健滔
(上海大學, 上海 200072)
?
振動式壓電風能發電裝置的研究
吳 松,張健滔
(上海大學, 上海 200072)
建立了振動式壓電風能發電裝置在風流場中的有限元分析模型。基于標準k-ε模型進行了風流場仿真分析,并通過系統耦合實現了風流場和發電裝置固體之間的雙向耦合分析。獲得了壓電發電裝置在風流體作用下的振動特性結果,結果顯示:發電裝置在流場中徑向放置比其他放置方式能產生更多的電能。制作了壓電發電裝置,并在微型風洞中進行了實驗。結果表明,發電裝置在風場中徑向放置時產生的電壓明顯比其他放置方式高,當風速為15 m/s時,徑向放置的輸出電壓峰峰值大約是軸向放置的兩倍。
壓電發電裝置;流固耦合;振動;有限元
0 引 言
近年來,隨著無線傳感網絡以及微型電子設備的飛速發展,對這些設備的供能成為迫切需要解決的問題。傳統的化學電池供能具有其不足,例如電池體積大、能量密度低、使用壽命有限、 需定期更換、成本高、舊電池處理不當會對環境產生污染。因而從環境中尋找新的能源替代傳統電池供電成為國內外研究的熱點[1-4]。
風能作為自然界中的綠色可再生能源,安全、清潔、資源豐富、取之不竭,存在很大的利用價值。微型風能發電裝置可將風動能轉變為電能進而為微電子設備供能,其具有廣闊的發展前景。其中壓電式風能發電裝置由于具有結構簡單、能量密度大、無電磁干擾、啟動風速低、易于微型化等特點,國內外學者都展開了相應的研究[5-8]。
從結構特點來看,壓電式風能發電裝置可分為渦輪旋轉式和風致振動式兩種。Ying Yang等人提出了一款渦輪旋轉式壓電風能發電裝置,其通過風帶動旋轉裝置,進而使球跳動并撞擊壓電懸臂梁變形,從而產生電荷[9]。Karami等研制了一款微型風力渦輪發電裝置,其在轉動元件和壓電懸臂梁的末端都裝上永磁體,轉動元件通過永磁體的相互作用帶動壓電懸臂梁往復振動,從而產生電能[10]。D. St. Clair從樂器口琴獲得啟發,設計了一款微型自激振動壓電風能發電裝置[11]。Xue-Feng He提出了一款低啟動風速的壓電振動風能發電裝置,其通過風引起金屬懸臂梁撞擊擋板產生沖擊效果,進而致使壓電發電裝置振動,發電裝置的啟動風速為3.2~3.4 m/s[12]。
振動式壓電風能發電裝置由于其結構簡單、啟動風速較低等特點,受到了研究者的青睞。但如何提高發電裝置的能量轉換效率是一個值得研究的問題。本文將對振動式壓電風能發電裝置在流場中的放置方式對能量采集效率的影響進行研究。建立了壓電風能發電裝置在流場中的有限元分析模型,分析了其在流場中不同放置方式下的應變結果,并在小型風洞中測試了發電裝置在不同放置方式下的輸出電壓。結果表明:發電裝置在流場中合理放置能有效地提高其能量收集性能。
1 流固耦合有限元分析模型
振動式壓電風能發電裝置工作過程中涉及兩個能量轉換過程:空氣動能致使發電裝置的壓電元件產生振動,風能轉換為機械能;然后再利用壓電材料的正壓電效應將機械能轉換為電能。在能量的轉換過程中,壓電懸臂梁振動應變大小直接影響發電裝置的發電能力。因此,本文將建立振動式壓電風能發電裝置在風流場中的有限元分析模型,對比分析發電裝置在不同放置方式下的振動應變情況。
圖1是發電裝置在風流場中的放置方式示意圖。在同一平面內,通過改變壓電裝置與風向所成夾角α來變化壓電裝置的放置方式。其中,當夾角α為0°時,壓電懸臂梁呈軸向放置;夾角α為90°時,壓電懸臂梁呈徑向放置。
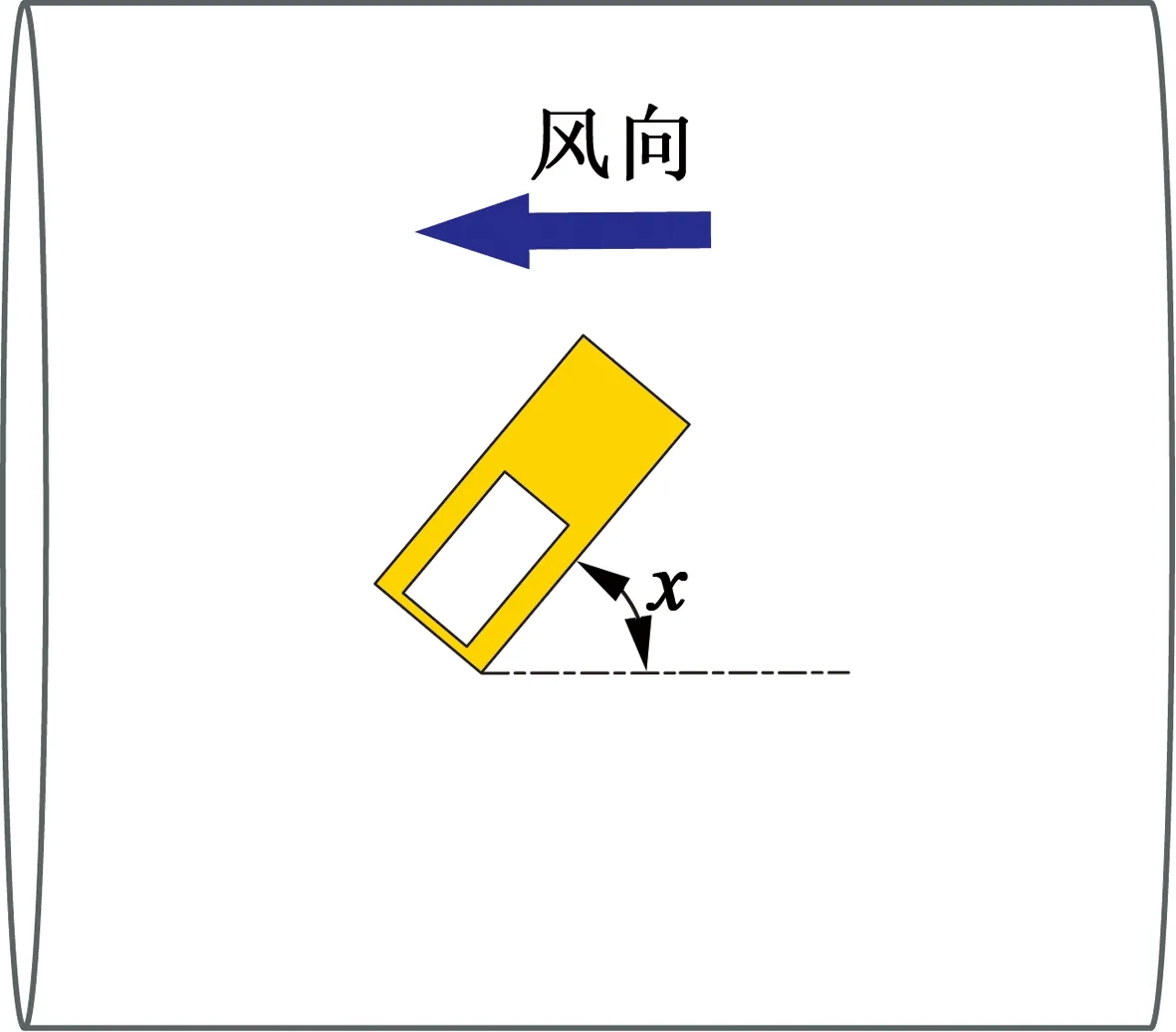
圖1 發電裝置在風流場中的放置方式示意圖
通過三維設計軟件建立有限元分析的幾何模型,如圖2所示。該幾何模型包括由壓電懸臂梁組成的固體域以及類似風洞腔體的流體域,流體域的尺寸與風洞實驗段尺寸相同。壓電懸臂梁在流場中放置方式包括四種:沿流體腔軸向放置、沿流體腔徑向放置、與風向呈45°放置和與風向呈90°放置。流體域中以空氣為介質,壓電懸臂梁的金屬體材料為純銅,壓電陶瓷片為PZT-5。
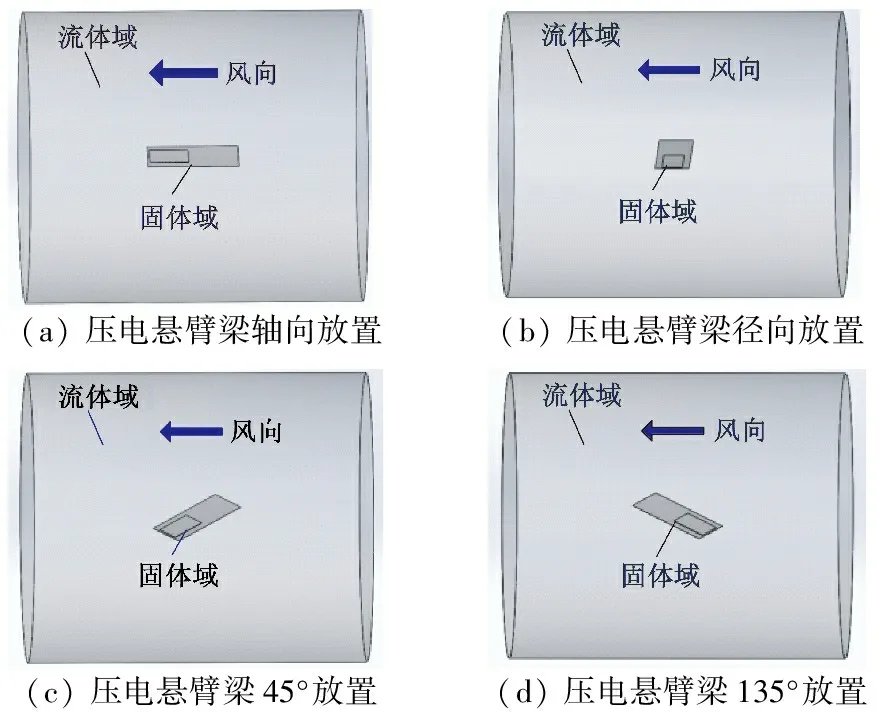
(a)壓電懸臂梁軸向放置(b)壓電懸臂梁徑向放置(c)壓電懸臂梁45°放置(d)壓電懸臂梁135°放置
圖2 有限元分析的幾何模型
將幾何模型導入有限元軟件中,流體域和固體域分別在Fluent模塊和Transient structural模塊下進行網格劃分,建立有限元模型如圖3所示。其中流體域的單元尺寸設為8 mm,網格單元數量達到111 387;固體域的單元尺寸設為1 mm,單元數量為2870。在流體計算中采用了標準k-ε模型。標準k-ε模型通過求解湍動能k方程和湍流耗散率ε方程,得到k和ε的解,再利用k和ε計算湍動粘度。標準k-ε模型具有較高的計算精度、較好的穩定性和計算經濟性,在湍流模型中得到了廣泛的應用。

(a)流體域(b)固體域
圖3 有限元模型
設置流場入口風速為10 m/s。流固耦合數值計算是一個雙向流固耦合的求解過程:先根據初始狀態,求解出流場的流動;然后通過系統耦合將耦合邊界上的流場計算結果傳遞給發電裝置,通過固體的瞬態結構分析求解出發電裝置的位移變化;瞬態分析結果又通過系統耦合傳遞給流場,之后又是流場分析計算。如此重復進行迭代計算,當求解結果趨于穩定,流場和瞬態分析數據交換停止,計算終止。
圖4為壓電懸臂梁在流場中四種放置方式下的應變結果圖,壓電懸臂梁應變最大的地方靠近固定端。對比四種放置方式下的結果,發現徑向放置時壓電陶瓷上的最大應變為軸向放置時壓電陶瓷上的最大應變的10倍;壓電懸臂梁45° 放置時壓電陶瓷上的最大應變為135° 放置時的3倍左右,且是軸向放置的4倍左右。即隨著夾角α從0° 增加到135°,壓電陶瓷上的最大應變先增大后減少。由壓電體所受應力及產生電場的本構關系可知,壓電體上的應變增加會致使產生的電場強度增強[1]。由此,結合壓電風能發電裝置有限元分析結果可知:發電裝置在流場中徑向放置時能產生更多的電能。
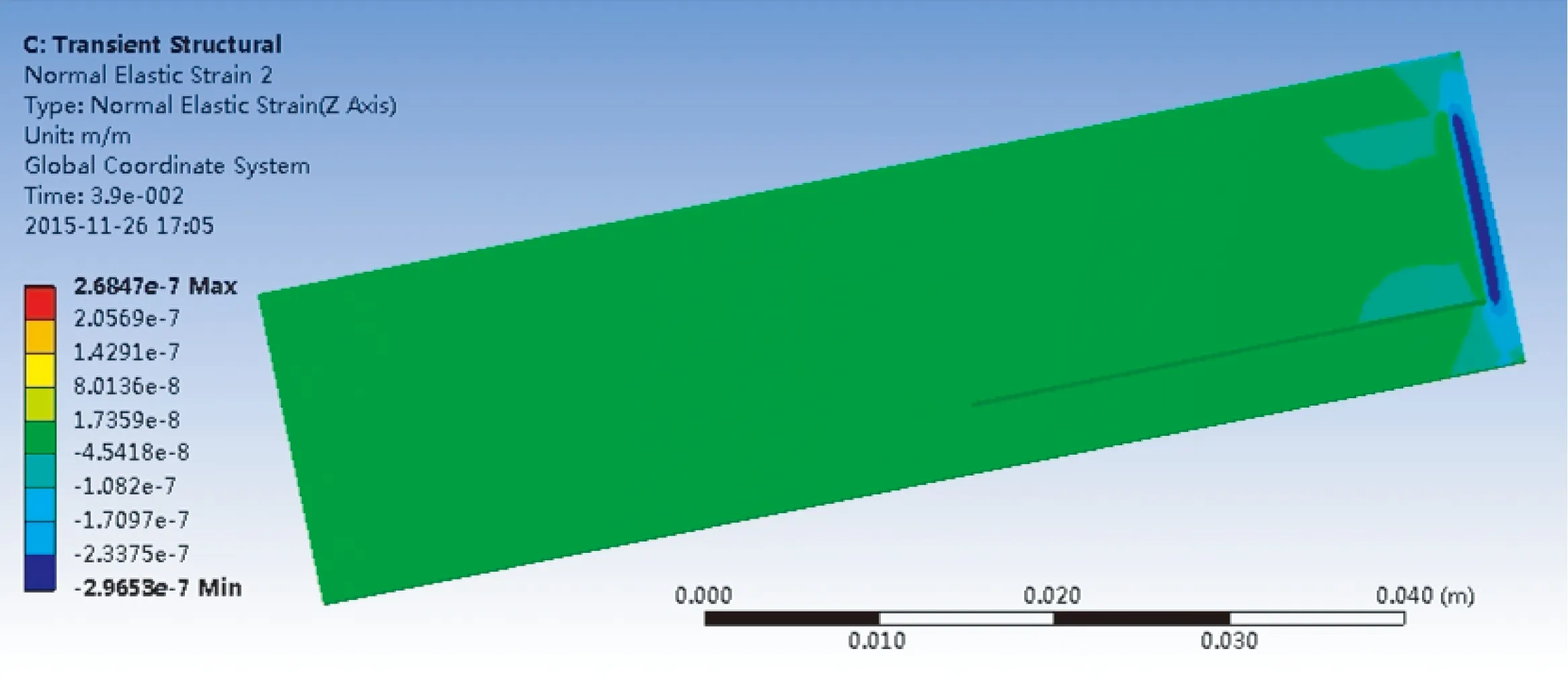
(a) 壓電懸臂梁軸向放置
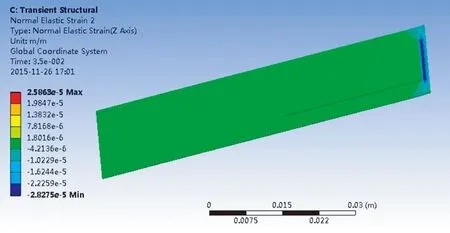
(b) 壓電懸臂梁徑向放置
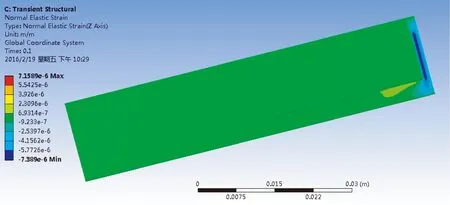
(c) 壓電懸臂梁45°放置
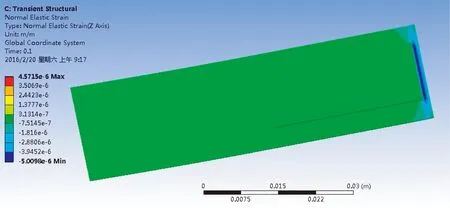
(d) 壓電懸臂梁135°放置
2 壓電發電裝置實驗
根據設計結果制作出壓電發電裝置,其中壓電材料采用壓電陶瓷PZT-5,尺寸為30 mm×16 mm×0.5 mm,基板材料為純銅,尺寸為70 mm×26.5 mm×0.2 mm。實驗設備如圖5所示,包括微型風洞、風速計(TASI-8818)、示波器(TBS 1102, Tektronix)。壓電發電裝置放置在風洞的透明實驗段,通過兩塊亞克力板夾持固定在一根螺柱上,如圖6所示,其中圖6(a)、圖6(b)、圖6(c)、圖6(d)分別是壓電懸臂梁軸向放置、徑向放置、45°和135°放置時的狀態。

圖5 實驗裝置圖

(a)壓電懸臂梁軸向放置(b)壓電懸臂梁徑向放置(c)壓電懸臂梁45°放置(d)壓電懸臂梁135°放置
圖6 壓電懸臂梁在風洞中的放置方式
測試出壓電發電裝置隨風速變化的曲線圖,如圖7所示。風速為從3 m/s增加到15 m/s,通過示波器記錄發電裝置的輸出電壓峰峰值,多次測量取平均。從圖7可以看出,隨著風速的增加,發電裝置的輸出電壓峰峰值也不斷增加。隨著發電裝置在風場中的夾角不斷增大,其產生的電壓先增大后減少,且當風速為15 m/s時,徑向放置時的輸出電壓峰峰值大約是軸向放置時的2倍。

圖7 風速與輸出電壓的關系曲線
3 結 語
本文建立了振動式壓電風能發電裝置在風流場中的有限元分析模型。利用標準k-ε模型來分析風流場,通過系統耦合實現了風流場和發電裝置固體之間的雙向耦合分析。獲得了發電裝置在風流體作用下的振動特性結果,結果表明:相對其他幾種放置方式,發電裝置在流場中徑向放置時能產生更多的電能。在微型風洞實驗裝置中,對分析結果進行了實驗驗證。實驗結果顯示:隨著發電裝置在風場中的夾角α的增大,其產生的電壓先增大后減少,且當風速為15 m/s時,徑向放置時的輸出電壓峰峰值大約是軸向放置時的2倍。
[1] 寧玉懷.壓電發電的能量轉化及儲能技術研究[D].長沙:中南大學,2010.
[2] PARK J C,PARK J Y.Asymmetric PZT bimorph cantilever for multi-dimensional ambient vibration harvesting[J].Ceramics International, 2013,39(1):5653-5657.
[3] 鄧冠前.基于壓電陶瓷的振動能量捕獲關鍵技術研究[D].北京:國防科學技術大學,2008.
[4] 王劍,郭吉豐,郭帥.壓電發電技術研究綜述.壓電與聲光[J].2011, 33(3): 394-398.
[5] KHALID M S,HOSSAM S A,MAZLAN A W,et al.Numerical simulation of confined vortex flow using a modifiedk-εturbulence model[J].CFD Letters, 2009,1(2): 87-94.
[6] KWON S D.A T-shaped piezoelectric cantilever for fluid energy harvesting[J].Applied Physics Letters, 2010,97(16): 1-3.
[7] 董志利,張廣明,徐飛.壓電陶瓷風力發電機的創新設計[J].微特電機,2014,42(1): 25-27.
[8] 周鐵英,鹿存躍,陳宇.毫米壓電微電機的發展與應用[J].微特電機,2005,33(12):41-44.
[9] YANG Ying,SHEN Qinlong.Rotational piezoelectric wind energy harvesting using impact-induced resonanceors[J].Applied Physics Letters, 2014,105(5): 053901.
[10] KARAMI M A,FARMER J R,INMAN D J.Parametrically excited nonlinear piezoelectric compact wind turbine[J].Renewable Energy,2013,50(3): 977-987.
[11] ST CLAIR D,BIBO A.A scalable concept for micropower generation using flow-induced self-excited oscillations[J].Applied Physics Letters, 2010,96(14): 144103.
[12] HE Xuefeng,GAO Jun.Wind energy harvesting based on flow-induced-vibration and impact[J]. Microelectronic Engineering,2013,111(11):82-86.
Piezoelectric Wind Energy Harvester Based on Vibration
WU Song, ZHANG Jian-tao
(Shanghai University, Shanghai 200072, China)
The finite element model for the piezoelectric wind energy harvester is developed. The wind flow field was simulated using the standard k-ε turbulence model. The fluid-structure interaction between the flow and the energy harvester was analyzed using system coupling. The vibration characteristics of the energy harvester were obtained, which was acted upon by the force exerted by the wind flow. The results show that the energy harvester placed along the radial direction can generate more electric power than that placed along the other direction. An energy harvester was fabricated and wind-tunnel experiments were carried out. The experimental results show that the energy harvester placed along the radial direction can generate higher voltage than that placed along the other direction. When the wind velocity is 15m/s, the output voltage peak-peak value of the harvester placed along the radial direction is about two times of that placed along the axial direction.
piezoelectric energy harvester; fluid-structure interaction; vibration; finite element method
2015-12-04
國家自然科學基金項目(51305248);上海市自然科學基金項目(13ZR1416900);上海高校青年教師培養計劃項目(ZZSD13051);上海大學創新基金項目(SDCX 2012025)。
TM315;TM359.9
A
1004-7018(2016)10-0010-03
吳松(1990-),男,碩士,研究方向為壓電能量收集器。

