豈是回避就能解決的？
——“減數或除數含有未知數的方程”教學引發的思考

江蘇南京市天正小學（瑯小分校）（210000） 王 軍

豈是回避就能解決的？
——“減數或除數含有未知數的方程”教學引發的思考

江蘇南京市天正小學（瑯小分校）（210000） 王 軍

在教學五年級的方程時，不少教師很是困惑∶遇到減數含有未知數和除數是未知數的方程時應該怎么教？各部分之間的關系要不要教？教師要站在學生的立場為學生和教材之間架設一座橋梁，讓學生順利達到彼岸。

回避 爭議 等式性質

對于“方程”這個單元，教材改編前爭議頗多，尤其是用等式性質解方程，對于減數是未知數和除數含有未知數時，很多教師認為教材回避了這個內容：“當學生根據等量關系列出方程解決實際問題時，難道告訴學生這種方程不好解，要求學生換一種數量關系再列出新的方程？”這顯然不是回避就能解決的。

真的是教材刻意回避嗎？我仔細研讀教材，覺得教材不出現這種情況，是為了減輕學生解決稍復雜方程的知識負擔。作為教師，完全可以在教材的基礎上進行適當的拓展，利用等式的性質還是能解決未知數為減數和除數的情況。

例1 解方程：9－x＝6

解：9－x－9＝6－9

方程兩邊同時減去9，等式右邊不夠減，因此無法進行。

仔細研究教材（如圖1）。

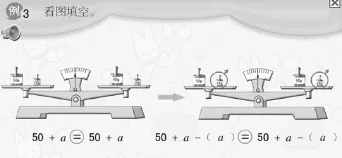
圖1

我們不難發現，教材給出了等式性質：等式兩邊同時加上了一個數a，仍然是等式。

方程的兩邊同時加上x雖然比較繁瑣，但是完全可以解釋，并不需要回避。

除數為x的情況也可以解釋：

例2 解方程：72÷x＝8

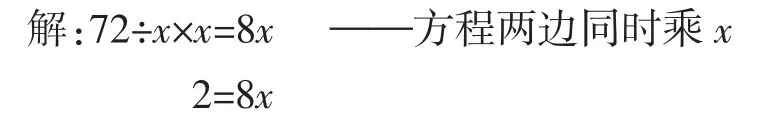
有教師提出：方程兩邊同時乘的x要不為0才行。也有教師認為：這樣計算對小學生來說有一定的困難，因為等式的性質涉及的只是同乘或同除同一個不為0的數，而x已經是一個代數式了。

我個人認為，在具體方程里，這里的x只表示的是一個數，而且是一個不為0的數。

當然，這樣計算對學生來說需要運用大量的等式性質，再加上比較煩瑣的過程，容易出錯。

能否從其他角度來解方程呢？答案是肯定的。完全可以利用等式的性質“等式兩邊都加上（或減去）同一個數或等式兩邊都乘以或除以（除數不為0）同一個數，等式仍然成立”來解減數或除數含有未知數的方程，不需要在方程左右兩邊同時加減或乘除含有x的代數式。

例3 解方程：9－x＝6

例4 解方程：12－2x＝3

在利用等式的性質解減數含有未知數的方程時，并沒有規定要減去方程左邊的數，所以完全可以引導學生減去方程右邊的數，使得方程的右邊為0。這樣，方程的左邊兩數之差為0，再已根據已學的知識“兩數相減差是0，則兩數相等”的特性，可以推斷出含有x的代數式的值。

例5 解方程：72÷x＝8

在利用等式的性質解除數含有未知數的方程時，可以引導學生在方程的兩邊同時除以方程右邊的數，使得方程的右邊為1，得到方程的左邊兩數之商為1后，再根據已學的知識“兩數相除商是1，則兩數相等”的特性，推斷出含有x的代數式的值。

為什么要違背學生的認知規律硬性規定用等式的性質去解方程呢？為什么就不能提供多種方法讓學生自由選擇呢？所以我在教學等式的性質時，發現大一部分學生都能靈活運用各部分之間的關系解題，于是我順其自然教授這種方法，再讓學生自由選擇，用自己喜歡的方法解方程。

其實，細心的教師會發現，2011國家教育部頒布的義務課程標準發生了一些變化——調整了這部分內容的標準，將原來的“會用等式的性質解簡單的方程（如3x＋2＝5，2x－x＝3）”改為“能解簡單的方程（如3x＋2＝5，2xx＝3）”，這就意味著對于解方程的方法一定不能一味地要求用等式的性質了，而是充分尊重學生個體需要，讓學生用喜歡和合適的方法解方程。

（責編 金 鈴）

G623.5

A

1007-9068（2016）35-008