Archimedean copula函數非參數估計法的改進
王 迪,李述山,莊緒園
(山東科技大學 數學與系統科學學院,山東青島 266590)
Archimedean copula函數非參數估計法的改進
王 迪,李述山,莊緒園
(山東科技大學 數學與系統科學學院,山東青島 266590)
針對Archimedean Copula函數的參數估計問題,文章利用Archimedean Copula函數的對稱性提出了一種新的估計Kendall秩相關系數的非參數估計法,并且在理論上證明了新非參數估計法比傳統非參數估計法更有效。在此基礎上改進了Archimedean Copula函數參數的非參數估計法,并利用隨機模擬驗證了改進的有效性。
Archimedean Copula;非參數估計法;對稱性;有效性
0 引言
Copula函數[1]是一種通過數據和單個變量的邊緣分布函數來構造多個變量聯合分布函數的統計學方法。Copula函數的出現不僅將風險分析和多個變量時間序列分析推向了一個新的階段,同時作為一種刻畫變量之間相依結構的工具,在不能決定線性相關系數能否正確度量相關關系的情況下,為變量之間相依結構的分析帶來了很大方便。自從Copula函數被提出后,Copula函數在變量之間相關性分析、時間序列分析、金融風險及風險管理等方面得到了廣泛的應用[2]。Copula函數較多,常用的主要有兩類:橢圓Copula函數和阿基米德Copula函數,由于阿基米德Copula函數構造比較方便、計算簡單,另外還具有各種各樣的分布特征以及良好的統計性質,從而在金融領域得到廣泛運用。常用的Archimedean Copula函數有Gumbel Copula、Clayton Copula、Frank Copula、GS Copula等,這些Copula函數大多都是單參數函數,要更好的分析金融市場,必須首先得到較為精確的Copula函數,即要得到未知參數較好的估計。經過多年的研究,現如今對于單參數Archimedean Copula函數已有眾多估計方法[3]。通過對Archimedean Copula函數參數估計文獻的查閱,本文對其中的非參數估計法進行了改進。改進的方式就是改變樣本Kendall秩相關系數的估計量,使其包含了更多信息,進而讓非參數估計變得更加準確。
1 基本概念
定義[1]:設(X1,Y1),(X2,Y2)是互相獨立并且與(X,Y)具有相同分布的二維隨機向量,則稱τ=P[(X1-X2)(Y1-Y2)>0] -P[(X1-X2)(Y1-Y2)<0]為X和Y的Kendall秩相關系數。
定理1[1]:隨機變量X和Y的Copula函數是由生成元?生成的Archimedean copula函數,則X、Y的一致性相關系數Kendallτ為:
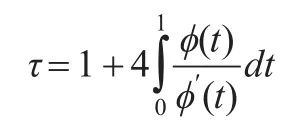
由定理1知,對于單參數的Archimedean copula函數來說,Kendall秩相關系數τ與其單參數θ具有一一對應關系。常用二元Archimedean copula函數參數值θ與Kendall秩相關系數τ的對應關系如表1所示:

表1 參數值θ與Kendall秩相關系數τ的對應關系
2 非參數估計法
定理2[4]:設(xi,yi)(i=1…n)為取自連續隨機向量(X,Y)的樣本,則Kendall秩相關系數τ的估計量為:
推論1:連續隨機向量(X,Y)有Archimedean copula函數 C(u,v)=C(F(x),G(y)),設 ui=F(xi),vi=G(yi),則Kendall秩相關系數τ的估計量為:
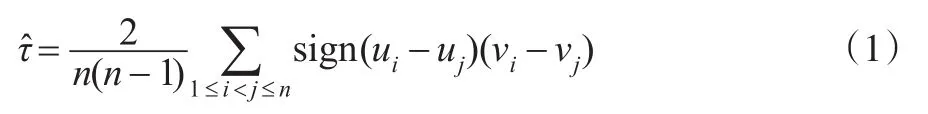
3 改進的非參數估計法
3.1 方法概述
通過Archimedean copula函數的生成元和表達式不難看出,Archimedean copula函數具有對稱性,即C(u,v)=C (v,u)。
定理3:若(ui,vi)和(uj,vj)是獨立同分布于C(u,v)的,則(ui,vi)和(vj,uj)也獨立同分布于C(u,v)。
推論2:由定理3可知如下等式成立:
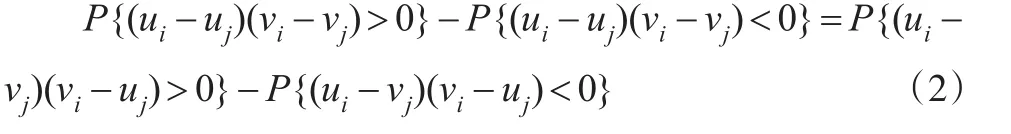
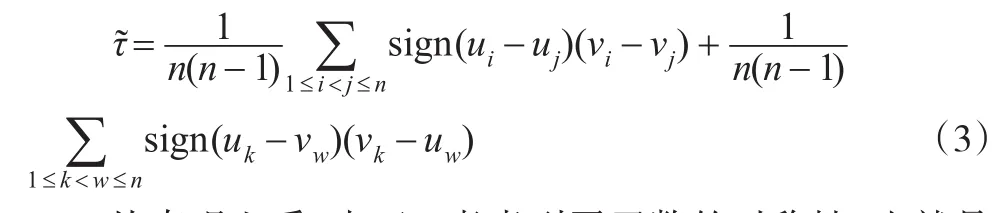
3.2 估計量的性質
(1)無偏性
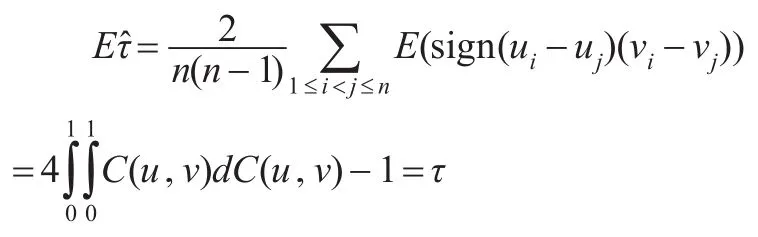
證明:為了使證明更具一般性,引入兩個均大于0的常數α,β定義如下:
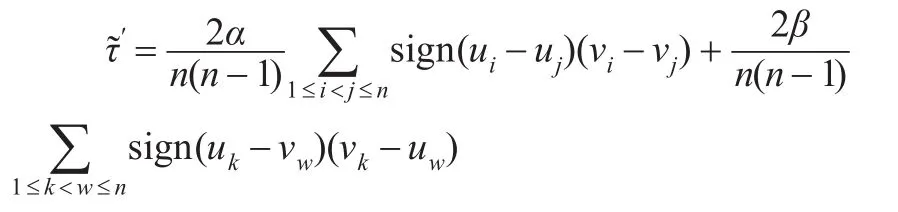
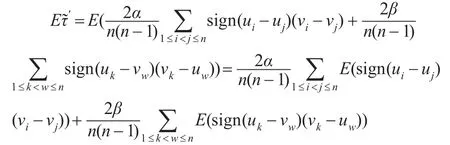
由于Archimedean copula函數具有對稱性,利用式(2)可得:
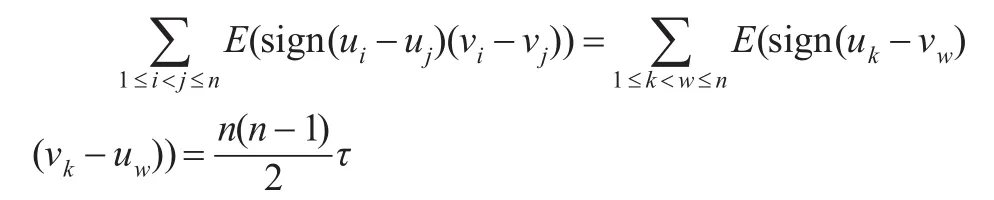
故可得:
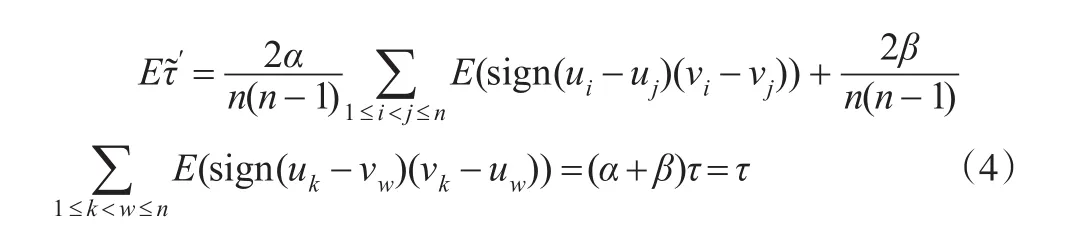
(2)有效性
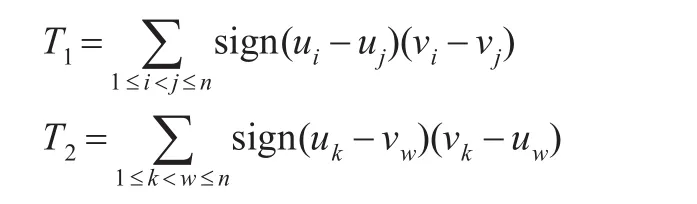
由Archimedean copula函數的對稱性可知:
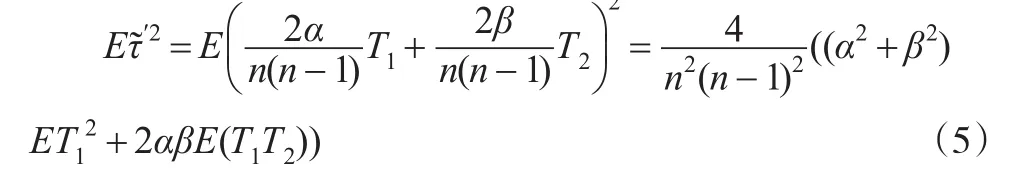
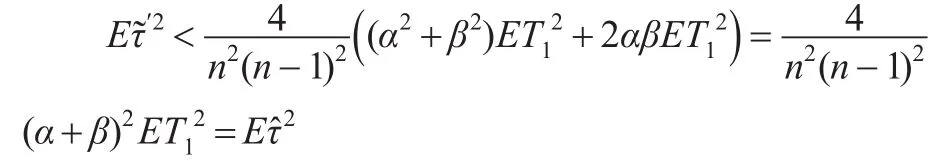
證明:討論α和 β的取值,考慮式(5)中的部分式子:
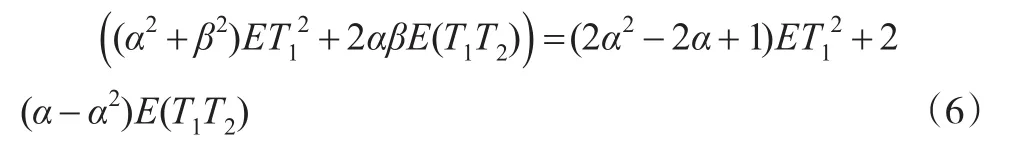
上式對α求導得:2(2α-1)ET12-2(2α-1)E(T1T2)=2 (2α-1)(ET12-E(T1T2)),由于已知E(T1T2) 由于Archimedean copula函數數量眾多且性質相似,所以本文以Gumbel Copula函數為例進行數據模擬研究。其表達形式如下:其中θ?[1,¥) 本文數據模擬思路是分別取θ為0.5,1,1.5,2,2.5和3,對于每一個給定的θ模擬產生隨機數據(ui,vi)(i=1…n),為了觀察樣本容量對估計的影響,分別令n為100,1000和10000,然后利用得到的隨機數據用兩種估計方法依次估計θ,每種方法估計m=1000次,將第i次的估計值記作i,最后求估計的絕對誤差結果如表2所示: 表2 參數估計結果 由表2可得如下結論: (1)對于同一個θ,改進的非參數估計比傳統非參數估計絕對誤差小。 (2)隨著n的增大,改進的非參數估計和傳統非參數估計的絕對誤差都越來越小。 綜上所述,本文利用Kendall秩相關系數的特征將對隨機向量樣本數據求Kendall秩相關系數轉化成了對其相應Archimedean Copula函數樣本數據求Kendall秩相關系數。在此基礎上根據Archimedean Copula函數的對稱性提出了新的Kendall秩相關系數估計量,使其相對于原先的估計量包含了更多信息,并且在理論上證明了新估計量比原先的估計量更有效。進一步利用新估計量改進了傳統的Archimedean Copula非參數估計法,并且通過隨機模擬驗證了改進的有效性。由于非參數估計方法簡單,計算量小,所以當樣本較大時,改進的非參數估計法是對Archimedean Copula進行參數估計的不錯選擇。 [1]Nelsen R B,Oregon P.An Introduction to Copulas[M].New York: Springer,1999. [2]張堯庭.連接函數(copula)技術與金融風險分析[J].統計研究,2002,(4). [3]杜江,陳希鎮.Archimedean Copula函數的參數估計[J].科學技術與工程,2009,(3). [4]李霞.Archimedean copula函數模型選擇方法的改進[J].統計與決策,2014,(13). (責任編輯/易永生) O212.7 A 1002-6487(2016)21-0016-03 王 迪(1991—),男,山東濱州人,碩士,研究方向:金融統計。 李述山(1966—),男,山東蒙陰人,博士,教授,研究方向:統計學。4 隨機模擬
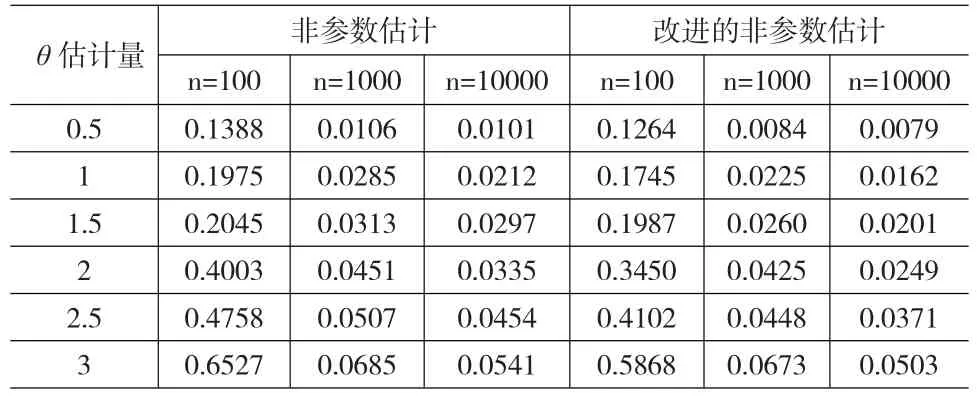
5 結論

