單層網(wǎng)殼沖擊動態(tài)響應(yīng)相似律與數(shù)值模擬驗證

姜正榮， 鐘渝楷， 石開榮

(1. 華南理工大學(xué) 土木與交通學(xué)院，廣州 510640； 2. 華南理工大學(xué) 亞熱帶建筑科學(xué)國家重點實驗室，廣州 510640)

?

單層網(wǎng)殼沖擊動態(tài)響應(yīng)相似律與數(shù)值模擬驗證

姜正榮1,2， 鐘渝楷1， 石開榮1,2

(1. 華南理工大學(xué) 土木與交通學(xué)院，廣州 510640； 2. 華南理工大學(xué) 亞熱帶建筑科學(xué)國家重點實驗室，廣州 510640)

根據(jù)Π定律，考慮應(yīng)變率強化效應(yīng)，通過修正速度相似條件得到修正模型，推導(dǎo)網(wǎng)殼在頂點受沖擊時的相似律表達(dá)式。利用非線性有限元軟件LS-DYNA建立與已有文獻(xiàn)相同的模型，驗證有限元分析的可靠性；在此基礎(chǔ)上，建立滿足相似律的不同幾何縮比凱威特-聯(lián)方型單層網(wǎng)殼數(shù)值模型，并分別考慮網(wǎng)殼未破壞和破壞的情況，對相似律進行驗證。研究表明：考慮應(yīng)變率效應(yīng)的修正模型能較好地預(yù)測原型的動態(tài)響應(yīng)，結(jié)果具有較好的精度；當(dāng)應(yīng)變率越高和幾何縮比越小時，未修正模型預(yù)測誤差越大；工程實踐中，模型和原型需考慮滿足應(yīng)變率強化效應(yīng)的相似律。

單層網(wǎng)殼；動態(tài)響應(yīng)；相似律；應(yīng)變率效應(yīng)；數(shù)值模擬

網(wǎng)殼結(jié)構(gòu)被廣泛應(yīng)用于體育館、展覽館等人員密集的建筑中。除了尋常的風(fēng)荷載、屋面荷載和地震作用，網(wǎng)殼結(jié)構(gòu)還可能遭到爆炸、沖擊等短時超強荷載的作用。經(jīng)歷9.11事件后，對該類結(jié)構(gòu)沖擊動態(tài)響應(yīng)的研究也越來越具有現(xiàn)實意義，特別是對重要大跨度公共建筑的防恐怖襲擊更具有重要意義。

工程實踐中，為深入研究結(jié)構(gòu)的失效破壞機理，同時節(jié)省成本，往往需進行縮尺模型試驗。對網(wǎng)殼的抗沖擊性能，早期的研究，主要集中于試驗和數(shù)值模擬方面。李海旺團隊[1-2]率先對K8型網(wǎng)殼在頂點沖擊載荷下的動力響應(yīng)進行試驗研究。王多智等[3-5]對K8型單層網(wǎng)殼進行了失效機理、失效模式及較為全面的參數(shù)研究，并用試驗驗證了有限元模型的可靠性。吳長[6]分析了網(wǎng)殼受落石沖擊時的動力響應(yīng)，并進行了縮尺模型的沖擊試驗。然而，上述工作均未涉及相似律的研究。

本文對凱威特-聯(lián)方型單層網(wǎng)殼受頂點沖擊的相似律進行推導(dǎo)，并考慮材料應(yīng)變率效應(yīng)，得到量綱統(tǒng)一的相似律函數(shù)；利用非線性有限元軟件LS-DYNA建立與已有文獻(xiàn)相同的模型，驗證有限元分析的可靠性，然后對不同縮比的模型進行數(shù)值模擬，驗證相似律分析結(jié)果的正確性。

1 相似律推導(dǎo)

網(wǎng)殼頂點受沖擊物沖擊涉及到幾何因素、材料因素、邊界條件和碰撞因素等。由于邊界條件相同，沖擊姿態(tài)相同，忽略碰撞過程中的熱效應(yīng)，相關(guān)參數(shù)可簡化為沖擊物和網(wǎng)殼的特征參數(shù)。對沖擊物，其尺寸參數(shù)設(shè)為aq,aq1,…,aqn；材料參數(shù)：密度ρq，彈性模量Eq，泊松比νq，動態(tài)屈服應(yīng)力Ydq；質(zhì)量塊速度vq。對網(wǎng)殼，有幾何參數(shù)：鋼管直徑Dt，壁厚tt，跨度lt，矢高ft；材料參數(shù)：密度ρt，彈性模量Et，泊松比νt，動態(tài)屈服應(yīng)力Ydt。

網(wǎng)殼頂點豎向位移wt為上述參數(shù)的函數(shù)，有

wt=f(aq,aq1,…,aqn,ρq,Eq,νq,Ydq;

Dt,tt,lt,ft,ρt,Et,νt,Ydt;vq)

(1)

取沖擊物特征長度aq，密度ρq和網(wǎng)殼動態(tài)屈服應(yīng)力Ydt為基本量，故得到無量綱函數(shù)關(guān)系：

(2)

考慮到已有模型試驗均采用鋼材，故此處模型和原型采用相同材料，同時考慮原型和模型的幾何相似，上述關(guān)系簡化為：

(3)

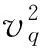
由于鋼材屬于應(yīng)變率敏感材料，不同大小的模型即使應(yīng)力相同，應(yīng)變率亦有可能不同，模型越小應(yīng)變率越敏感[8]。大量研究表明，由于材料應(yīng)變率敏感性和材料失效等因素的影響，當(dāng)結(jié)構(gòu)受沖擊載荷時往往不遵從相似律。為此，文獻(xiàn)[9-10]提出了相關(guān)改進方法，即通過修改模型的沖擊速度，使得模型與原型在考慮應(yīng)變率效應(yīng)后滿足相似律。

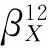
(4)

(5)

故

(6)

(7)

(8)

(9)

由式(8)、(9)得

(10)

鋼材的應(yīng)變率強化效應(yīng)用Cowper-Symonds模型表示[10]：

(11)

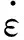
式(11)可用Norton-Hoff方程代替，將Yd和Ys的關(guān)系表達(dá)為指數(shù)函數(shù)關(guān)系[11]，有

(12)

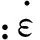
圖1給出不同應(yīng)變率下Cowper-Symonds和Norton-Hoff應(yīng)力比的對比，可以發(fā)現(xiàn)，兩者的誤差較小，故用Norton-Hoff方程代替Cowper-Symonds是合理的。

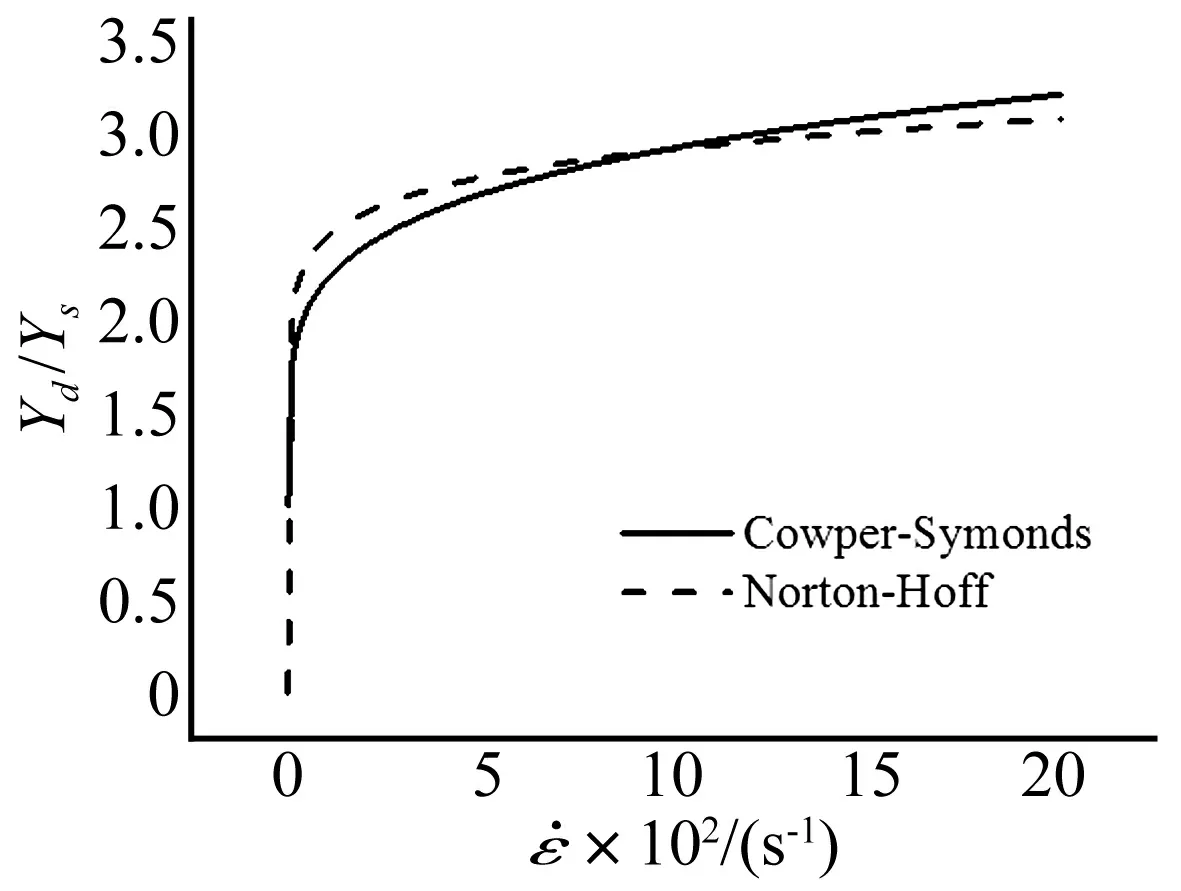
圖1 Cowper-Symonds和Norton-Hoff本構(gòu)關(guān)系對比[10]Fig.1 Comparison of constitutive law between Cowper-Symonds and Norton-Hoff [10]

由式(10)、(12)得到：

(13)

將式(8)代入式(13)得

(14)

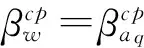
(15)

考慮接觸力F和接觸時間t,由力與應(yīng)力的關(guān)系和式(15)，得

(16)

時間與應(yīng)變率成倒數(shù)關(guān)系，由式(9)和(15)得

(17)

將d=0.077和幾何縮比代入式(15)～(17)，得應(yīng)力、力和時間縮放因子，如表1所示。

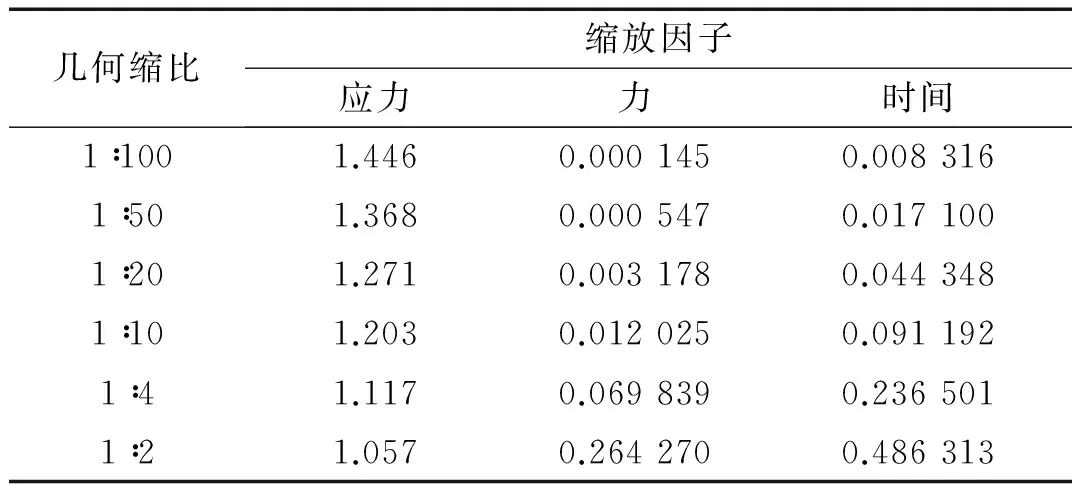
表1 不同幾何縮比時應(yīng)力、力和時間縮放因子

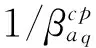
2 數(shù)值算例驗證

2.1 有限元模型驗證與計算模型建立

采用文獻(xiàn)[2]的網(wǎng)殼沖擊試驗進行數(shù)值算例比較驗證。試驗?zāi)Ｐ蜑镵8型單層網(wǎng)殼，直徑1 202 mm，矢高248.7 mm，桿件采用直徑為4 mm的鋼絲，節(jié)點取20 mm鋼球，沖擊物為0.35 kg落錘，落錘受重力作用自由落體沖擊網(wǎng)殼，釋放高度分別為1 m和1.5 m。

利用LS-DYNA軟件建立有限元模型。由于該試驗并未對桿件進行材料力學(xué)性能試驗，故數(shù)值模擬采用理想鋼材參數(shù)進行分析。桿件采用BEAM161單元，每根桿件劃分為3個單元，本構(gòu)關(guān)系采用分段線性塑性模型“MAT_PIECEWISE_ LINEAR _PLASTICITY”，密度ρ=7 850 kg/m3，泊松比ν=0.3，彈性模量E=206 GPa，切線模量Et=2.18 GPa，屈服強度為235 MPa，失效應(yīng)變?yōu)?.25，強化系數(shù)a=40 s-1，b=5，其本構(gòu)曲線如圖1中Cowper-Symonds所示。沖擊物采用SOLID165單元，本構(gòu)關(guān)系采用剛體“MAT_RIGID”，密度ρ=7 850 kg/m3，泊松比ν=0.3，彈性模量E=206 GPa。球節(jié)點采用質(zhì)量單元MASS166施加在各節(jié)點，整個模型施加重力加速度場，方向豎直向下。沖擊物與網(wǎng)殼接觸采用點面接觸(NODE-TO-SURFACE)。

試驗中測量7根桿件軸力(圖2)和沖擊接觸力時程曲線。數(shù)值模擬值和試驗值的比較分別如表2、表3和表4所示，沖擊接觸力時程曲線如圖3和圖4給出。

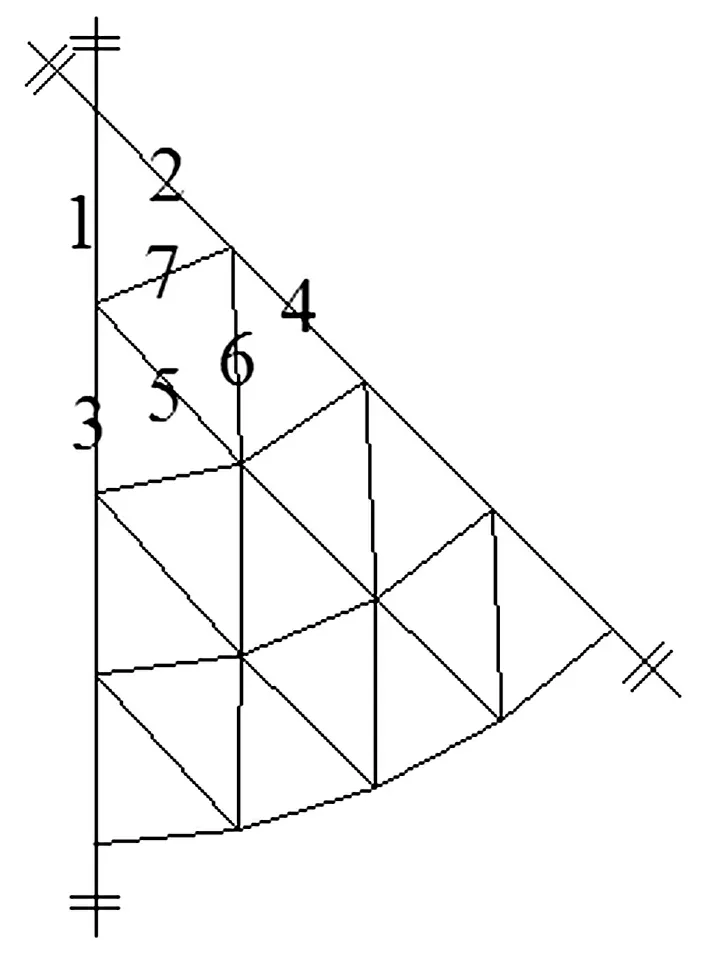
圖2 測量桿件Fig.2 Measuring bars

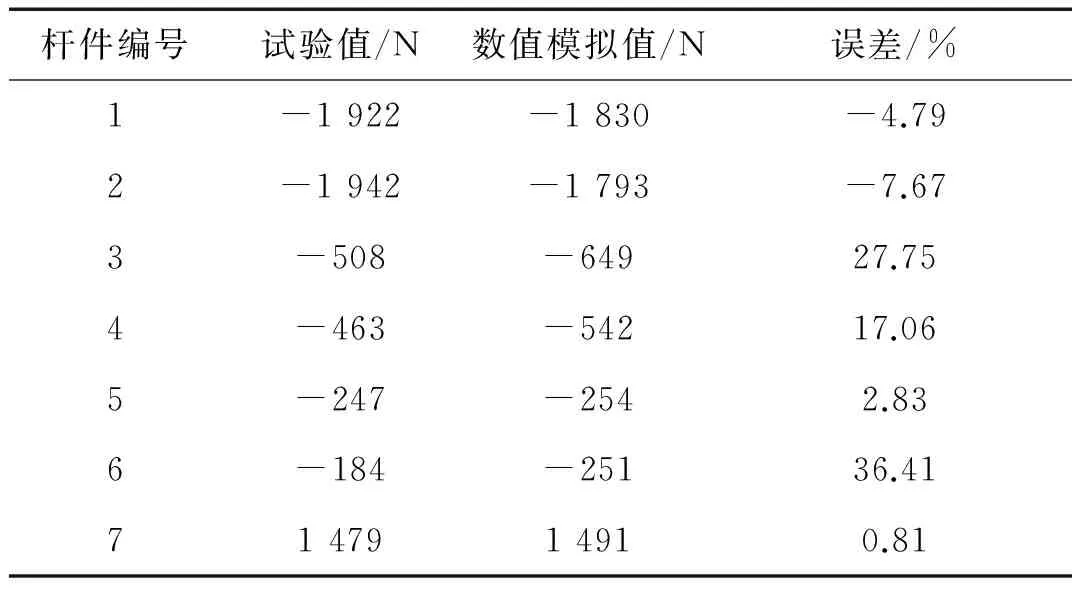
桿件編號試驗值/N數(shù)值模擬值/N誤差/%1-1922-1830-4.792-1942-1793-7.673-508-64927.754-463-54217.065-247-2542.836-184-25136.417147914910.81

由表2和表3可見，除個別數(shù)據(jù)誤差較大，桿件軸力峰值的模擬值與試驗值均吻合較好，軸力分布規(guī)律基本一致，對稱桿件的軸力對稱性較好。

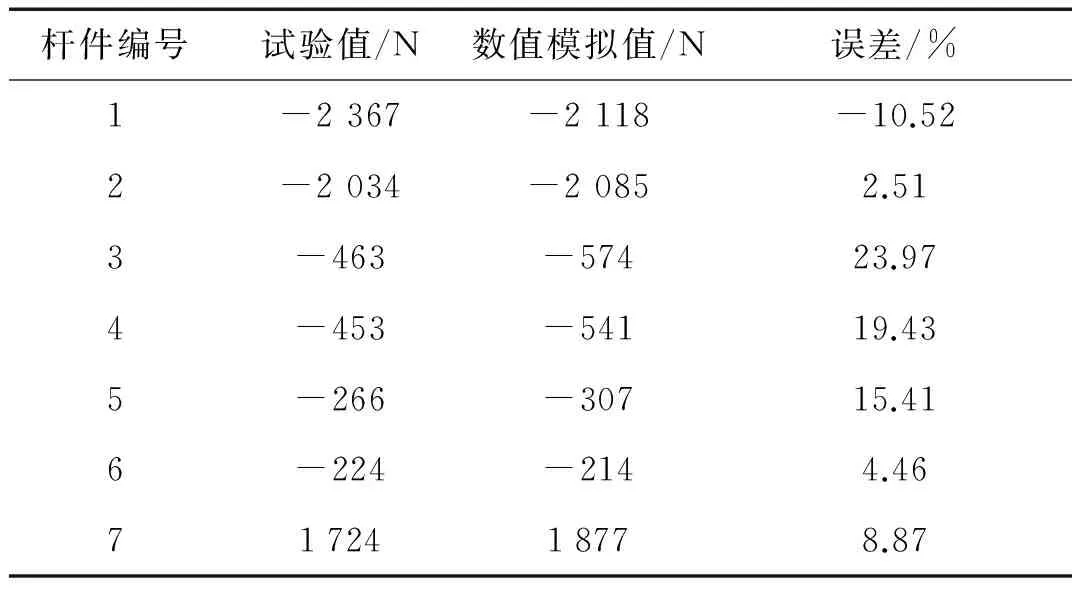
表3 桿件軸力數(shù)值模擬值和試驗值比較(釋放高度1.5 m)

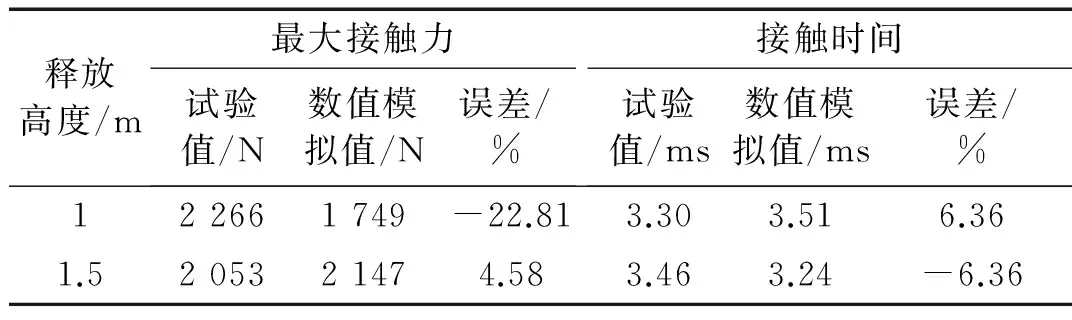
表4 接觸力數(shù)值模擬值和試驗值比較

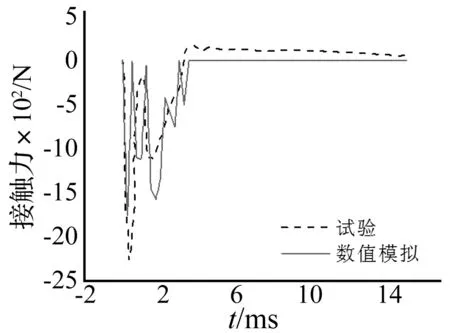
圖3 接觸力時程曲線對比(釋放高度1 m)Fig.3 Comparison of contact force-time curve (release height 1 m)

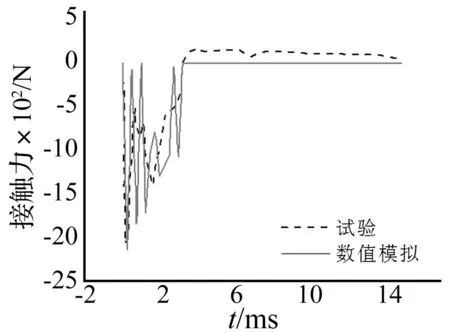
圖4 接觸力時程曲線對比(釋放高度1.5 m)Fig.4 Comparison of contact force-time curve (release height 1.5 m)

忽略接觸前的時間，由表4和圖3、圖4可見，數(shù)值模擬的沖擊接觸力峰值和持續(xù)時間均與試驗值對應(yīng)較好。由沖擊接觸力時程曲線的比較可知，沖擊力峰值對應(yīng)時間都在接觸后立即出現(xiàn)。綜上，有限元方法是可靠的。

對比文獻(xiàn)[2]的數(shù)值模擬結(jié)果，可以發(fā)現(xiàn)本文模擬精度較高。主要原因可能是文獻(xiàn)[2]未考慮材料應(yīng)變率效應(yīng)，只設(shè)置切線模量考慮塑性。另外，接觸算法選擇的不同和軟件版本的升級均對模擬精度有影響。

造成數(shù)值模擬值與試驗值有差異的主要原因可能是：實際沖擊過程會有材料熱能、摩擦等消耗，而有限元模型未予以考慮；有限元模型未考慮節(jié)點剛度的貢獻(xiàn)，忽略節(jié)點吸收的能量；沖擊時桿件及節(jié)點有累計損傷，沖擊時不一定正對節(jié)點沖擊等。

圖5所示，利用LS-DYNA軟件建立跨度60 m，矢跨比1/6的凱威特-聯(lián)方型單層球面網(wǎng)殼作為原型。外圍兩環(huán)為聯(lián)方型網(wǎng)格，其他為凱威特型網(wǎng)格。凱威特型網(wǎng)格的主肋和環(huán)肋采用φ180×8，斜桿采用φ168×6；聯(lián)方型環(huán)肋為φ168×5.5，斜桿為φ180×7，均為圓鋼管。沖擊物采用直徑為3 m，高度為1 m的圓柱體。除了沖擊物的本構(gòu)關(guān)系采用分段線性塑性模型和不考慮重力，其他材料參數(shù)和接觸設(shè)置與上述驗證模型一致。

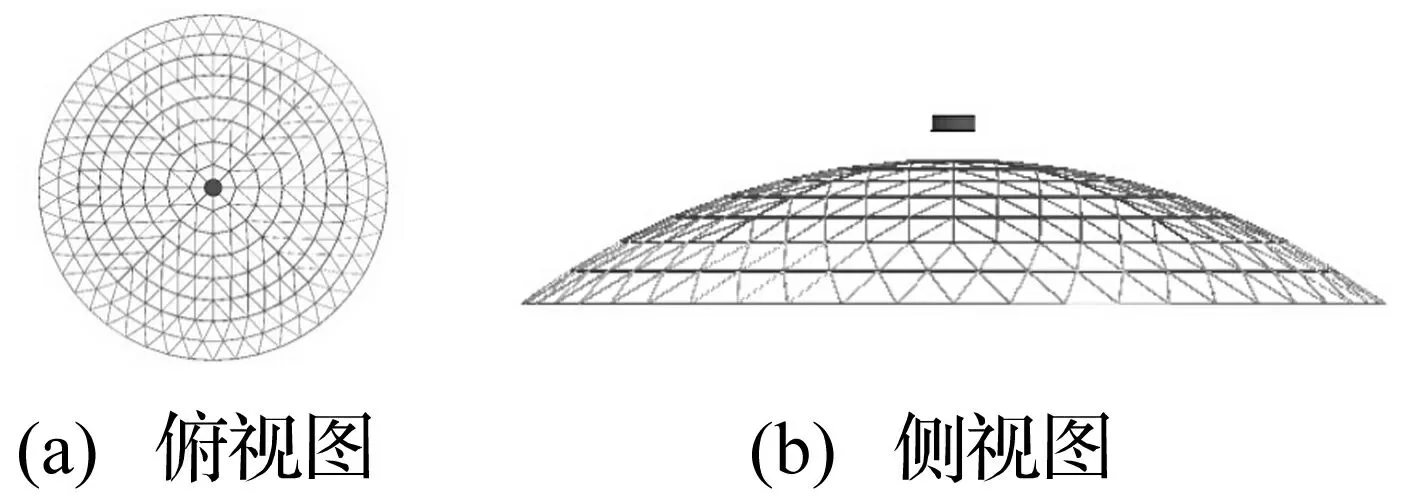
圖5 凱威特-聯(lián)方型單層網(wǎng)殼模型Fig.5 Model of Kiewitt-Lamella single layer reticulated shell

根據(jù)原型建立幾何縮比分別為1∶2、1∶4、1∶10、1∶20、1∶50和1∶100的模型，通過修正沖擊速度得到修正模型。由式(14)，代入鋼材常數(shù)d=0.077和幾何縮比，得到各個模型相對原型的速度縮放因子，如表5所示。

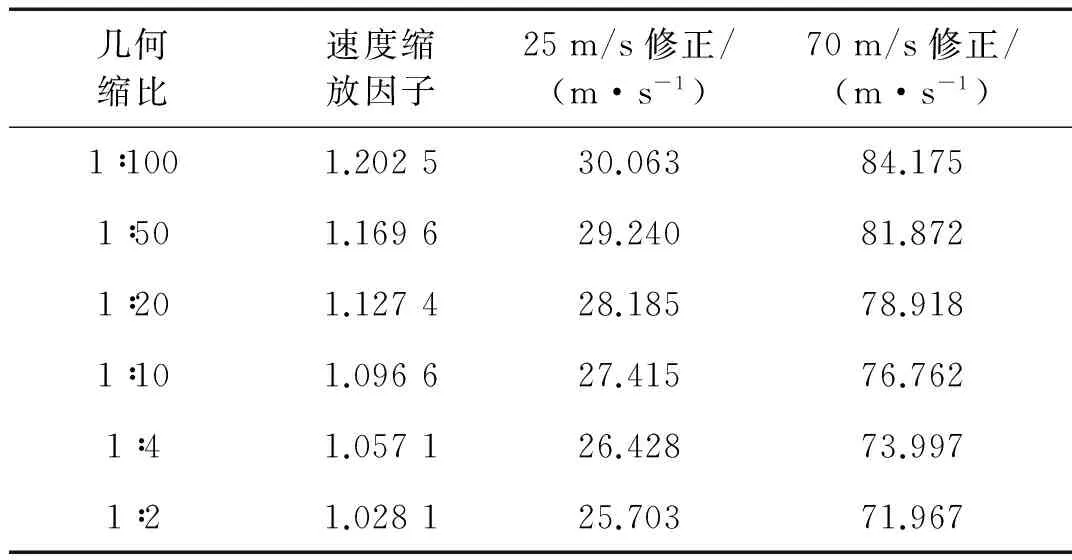
表5 速度縮放因子和修正速度

鋼材是應(yīng)變率敏感材料，網(wǎng)殼沖擊涉及到網(wǎng)殼失穩(wěn)，故初始條件的微小改變都可能導(dǎo)致結(jié)果產(chǎn)生很大差異。由于應(yīng)變率的估計很難，且修正速度采用的是平均等效應(yīng)變率，所以修正模型仍會有一定誤差，這在大量數(shù)值研究中均已被證實[9,12]。但相比未修正模型誤差較小，且符合工程精度要求。

考慮到遠(yuǎn)離沖擊點的區(qū)域動態(tài)響應(yīng)較小，選取中間三環(huán)進行分析，如圖6所示，節(jié)點用字母表示，桿件用數(shù)字表示。位移分析選取主環(huán)肋交點A、B和斜桿交點C，應(yīng)力和應(yīng)變分析桿件選取主肋桿件1、斜桿2和環(huán)肋3，以保證分析對象的全面性。

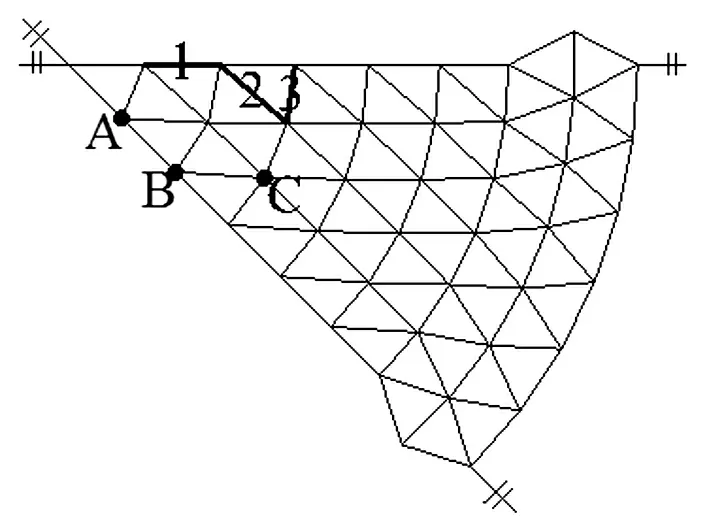
圖6 分析節(jié)點和桿件Fig.6 Nodes and bars analyzed

2.2 驗證算例一

考慮網(wǎng)殼未破壞情況，在此選取沖擊速度為25 m/s，網(wǎng)殼結(jié)構(gòu)局部倒塌，修正模型各縮比修正速度由表5給出。圖7給出各個幾何縮比下用修正和未修正模型預(yù)測原型豎向位移的對比結(jié)果。從中可見，修正模型和未修正模型都能較好地預(yù)測原型位移。由于應(yīng)變率的影響，幾何縮比越小，模型預(yù)測原型的誤差越大，未修正模型偏差比修正模型越大。當(dāng)幾何縮比為1∶100時，修正模型預(yù)測原型的C節(jié)點位移誤差為9.91%，而未修正模型誤差達(dá)到-20.27%，說明模型修正后精度較好。

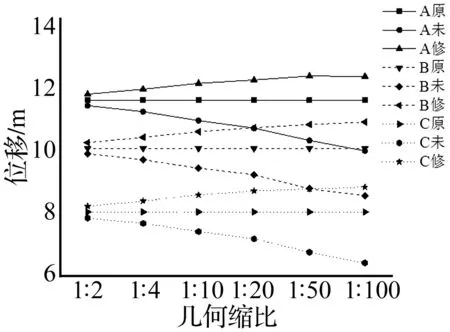
圖7 速度25 m/s時模型預(yù)測原型豎向位移結(jié)果對比Fig.7 Comparison of vertical displacement between corrected models and non-corrected models at v=25 m/s注：模型位移均已按幾何比例放大；原為原型，未為未修正模型，修為修正模型

表6和表7分別給出了修正模型預(yù)測原型應(yīng)力和應(yīng)變的結(jié)果。由相似結(jié)果可知，模型和原型應(yīng)變值在相似點處基本相同，應(yīng)力值通過縮放后也基本一致。結(jié)果表明：修正模型能很好地預(yù)測原型應(yīng)力和應(yīng)變值，除了少部分?jǐn)?shù)據(jù)，模型應(yīng)力預(yù)測最大誤差均低于7%，應(yīng)變預(yù)測誤差在10%以內(nèi)。由此說明，考慮應(yīng)變率效應(yīng)后的模型能較好地預(yù)測原型的應(yīng)力和應(yīng)變。

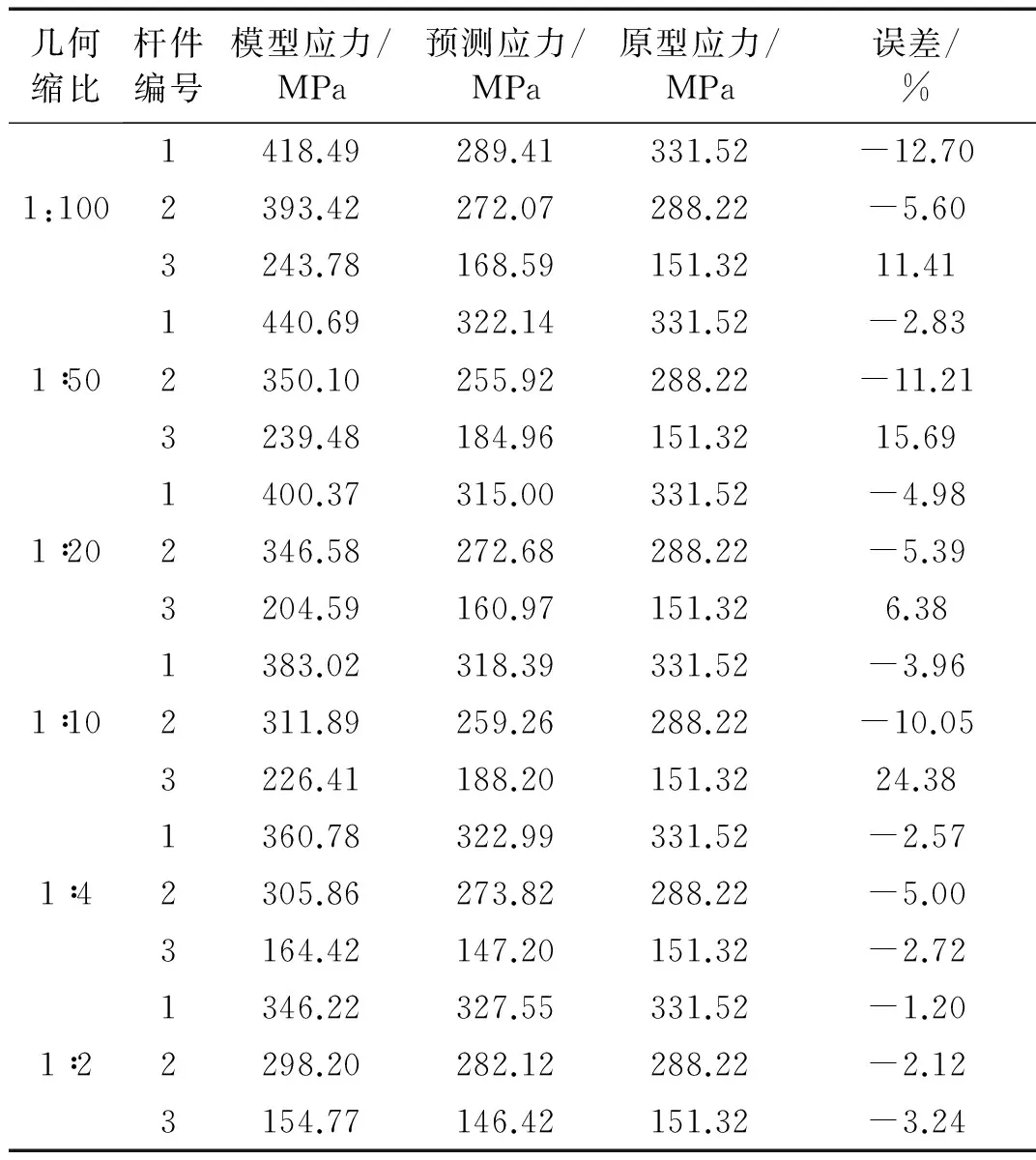
表6 速度25 m/s時修正模型預(yù)測原型應(yīng)力結(jié)果

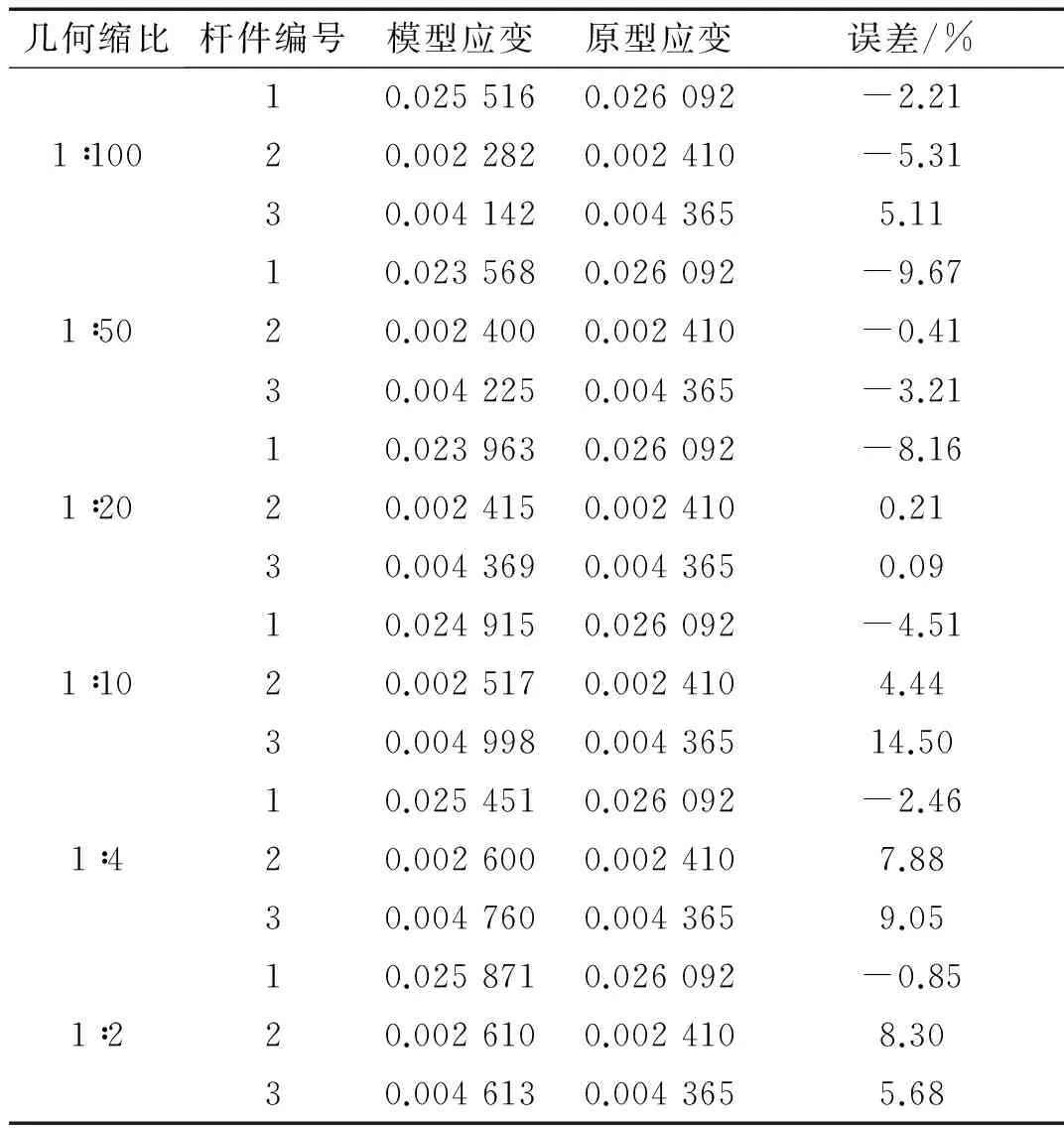
表7 速度25 m/s時修正模型預(yù)測原型應(yīng)變結(jié)果

表8和表9分別給出修正模型沖擊接觸力峰值和接觸時間的結(jié)果。模型接觸力和接觸時間按表1進行放大。結(jié)果顯示，在網(wǎng)殼未破壞時，修正模型預(yù)測原型的接觸力峰值和接觸時間的誤差均較小，說明用模型能夠較好預(yù)測原型的動態(tài)響應(yīng)。可能由于相似律未計及斷裂破壞的影響，網(wǎng)殼破壞時接觸面的情況十分復(fù)雜，模型預(yù)測原型的接觸力結(jié)果并不太理想，需要在接下來的研究中進行更深入的探討。

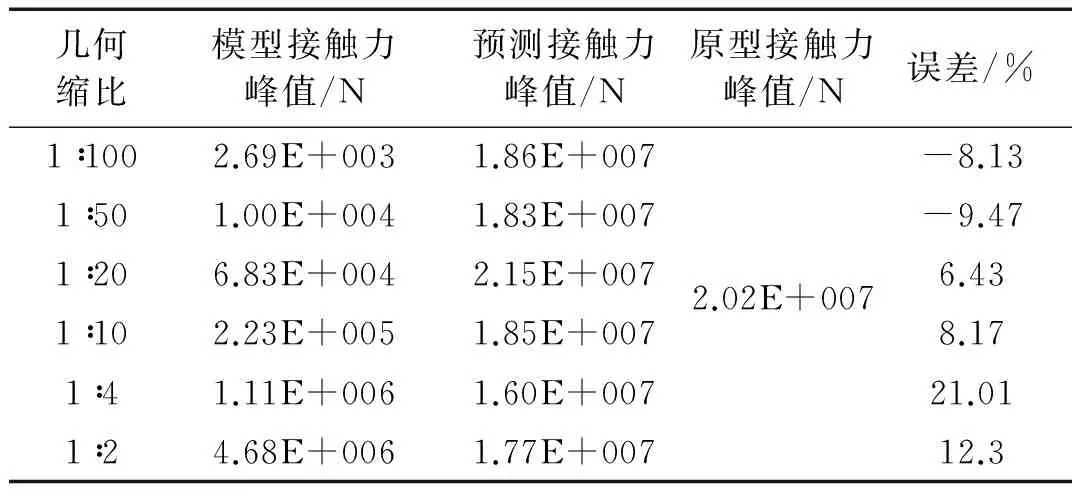
表8 速度25 m/s時修正模型預(yù)測原型接觸力峰值結(jié)果

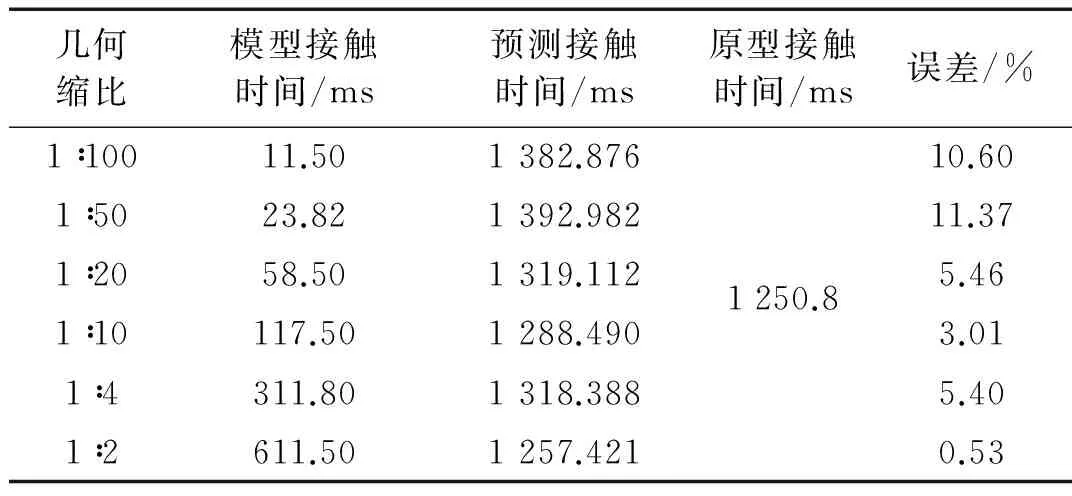
表9 速度25 m/s時修正模型預(yù)測原型接觸時間結(jié)果

2.3 驗證算例二

考慮網(wǎng)殼沖切破壞的情況，在此選取沖擊速度為70 m/s，修正模型各縮比修正速度見表5，結(jié)果如圖8所示。結(jié)果表明：修正模型在較高應(yīng)變率下仍能較好地預(yù)測原型位移，除了極個別點誤差較大，預(yù)測位移的誤差均小于10%，最小誤差僅為0.86%。而未修正模型在幾何縮比為1∶50和1∶100時分別出現(xiàn)大部倒塌和整體倒塌，與原型沖切破壞的結(jié)果相差甚大。如C節(jié)點，原型位移為0.115 8 m，幾何縮比為1∶50和1∶100的未修正模型預(yù)測結(jié)果分別為9.488 5 m和16.985 0 m，誤差達(dá)到一萬個百分點。說明在高應(yīng)變率和小幾何縮比的情況下，未修正模型已無法正確預(yù)測原型結(jié)果。修正模型在高應(yīng)變率和小幾何縮比的情況下均能得到較好結(jié)果，從而表明修正模型預(yù)測原型結(jié)果是可靠的。

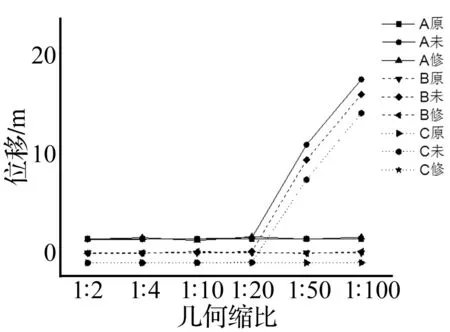
圖8 速度70 m/s時模型預(yù)測原型豎向位移結(jié)果對比Fig.8 Comparison of vertical displacement between corrected models and non-corrected models at v=70 m/s注：模型位移均已按幾何比例放大；原為原型，未為未修正模型，修為修正模型

修正模型預(yù)測原型的應(yīng)力和應(yīng)變結(jié)果分別見表10和表11。從中可知，網(wǎng)殼受到高速沖擊時修正模型仍能較好地預(yù)測原型的應(yīng)力和應(yīng)變，應(yīng)力預(yù)測誤差均小于9%，應(yīng)變預(yù)測誤差均小于8%，這在較高應(yīng)變率下的沖擊預(yù)測中具有較高精度。說明修正模型在高應(yīng)變率下仍能較好預(yù)測原型應(yīng)力應(yīng)變。

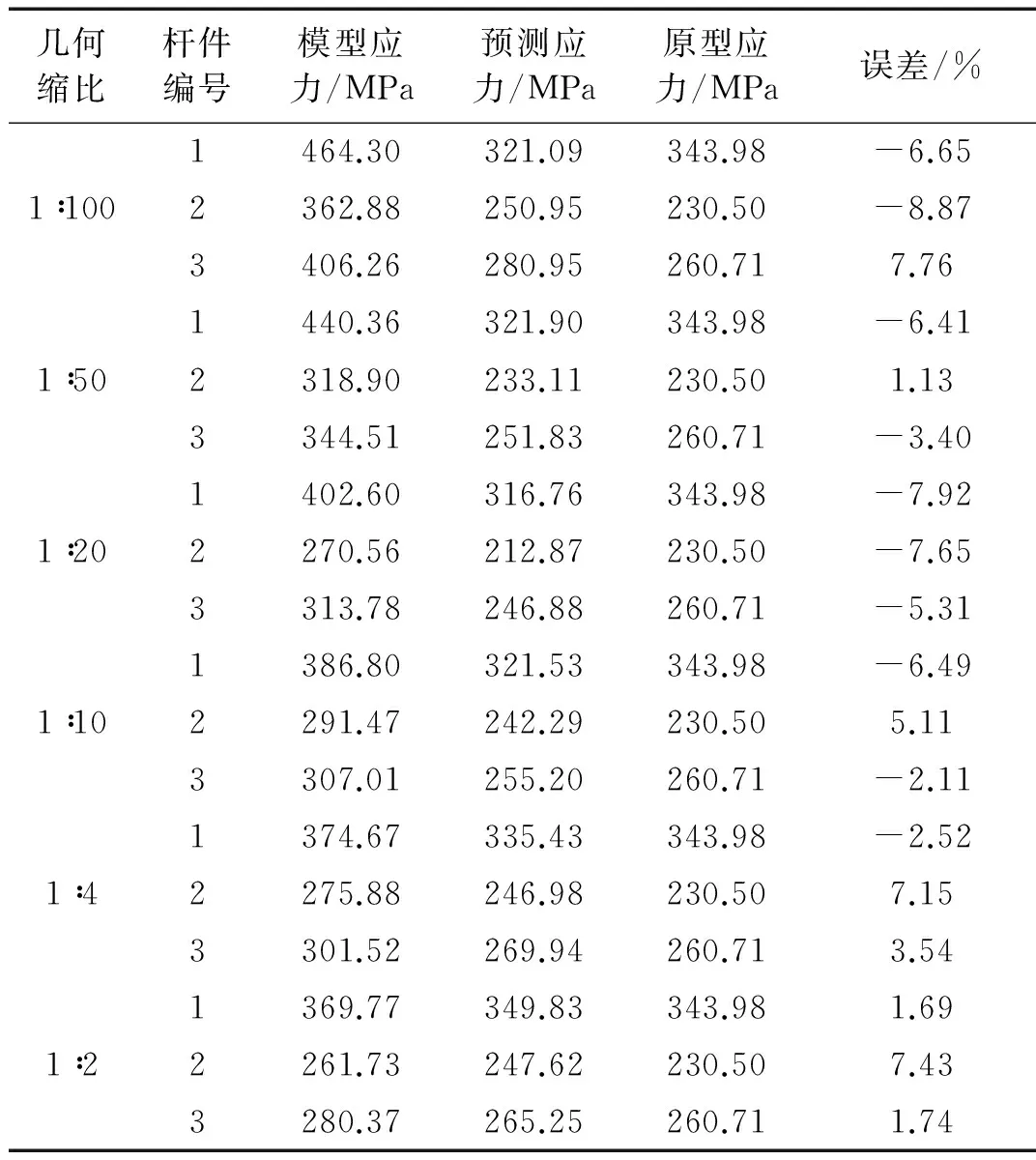
表10 速度70 m/s時修正模型預(yù)測原型應(yīng)力結(jié)果

圖9給出了不同速度下網(wǎng)殼主要桿件(第一圈環(huán)桿)的應(yīng)變率和未修正模型預(yù)測原型誤差的變化曲線。可以看出，隨著應(yīng)變率的增加，誤差在逐漸增大，由此說明未修正模型預(yù)測原型的誤差隨著應(yīng)變率的增大而變大。

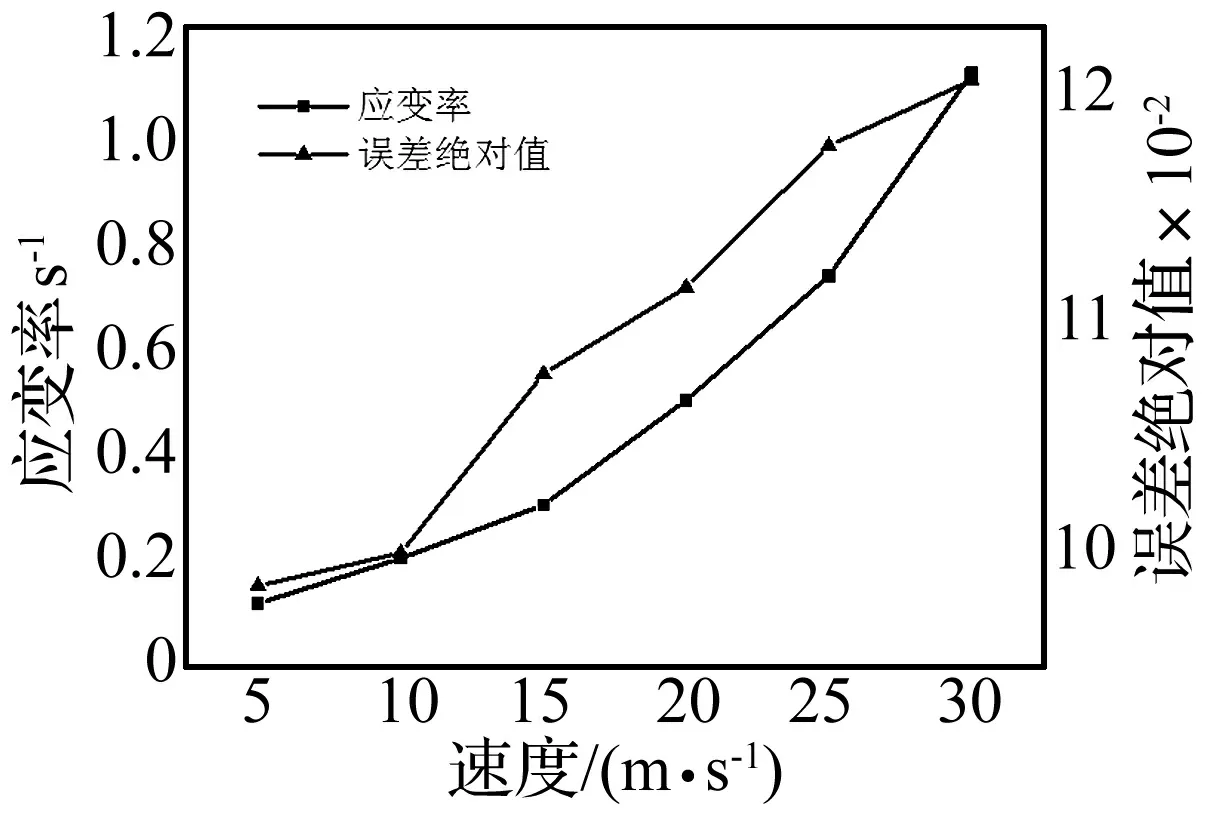
圖9 應(yīng)變率與預(yù)測誤差關(guān)系(未修正模型)Fig.9 Relationship between starin rate and prediction error(non-corrected models)

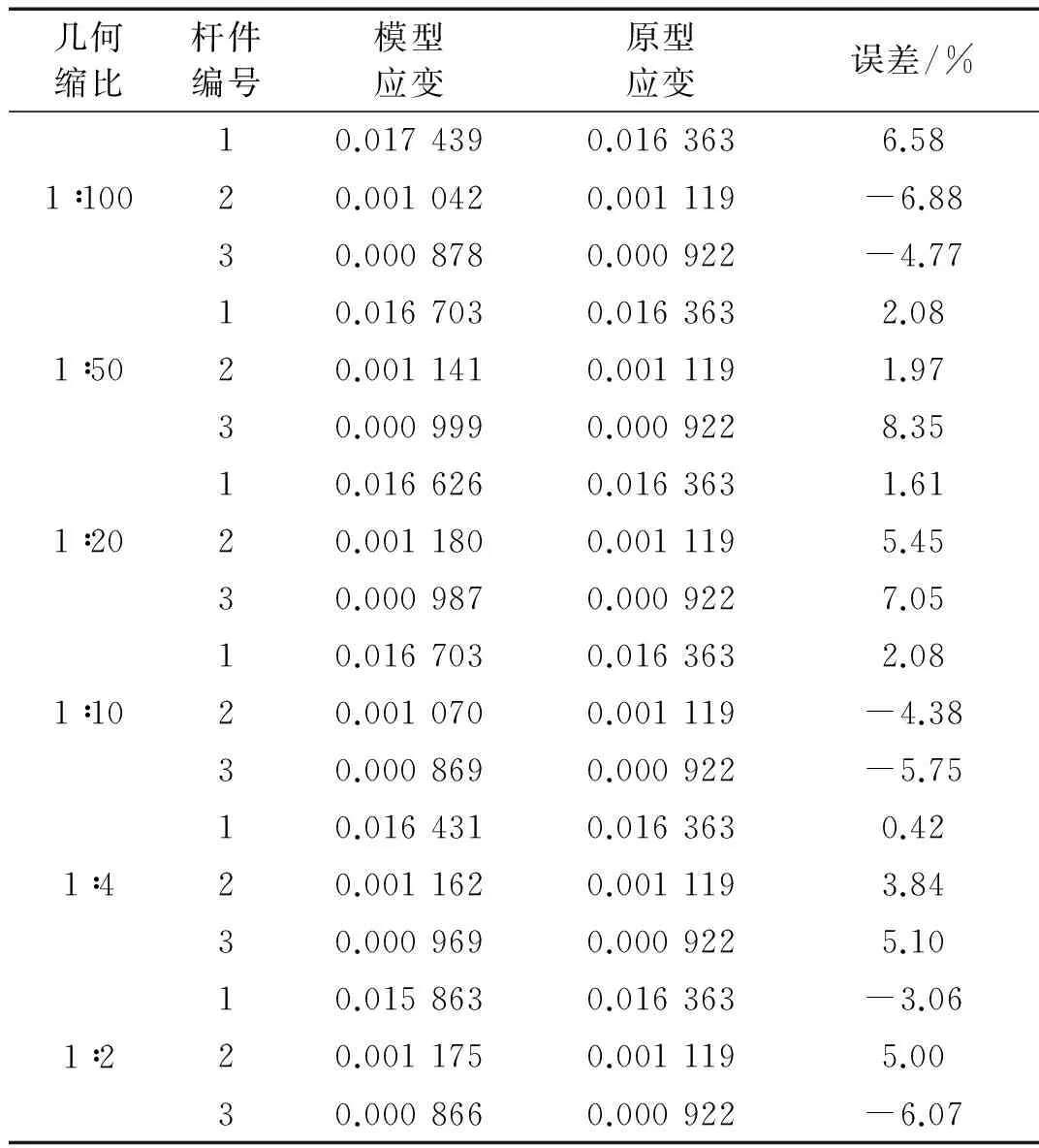
幾何縮比桿件編號模型應(yīng)變原型應(yīng)變誤差/%1∶10010.0174390.0163636.5820.0010420.001119-6.8830.0008780.000922-4.771∶5010.0167030.0163632.0820.0011410.0011191.9730.0009990.0009228.351∶2010.0166260.0163631.6120.0011800.0011195.4530.0009870.0009227.051∶1010.0167030.0163632.0820.0010700.001119-4.3830.0008690.000922-5.751∶410.0164310.0163630.4220.0011620.0011193.8430.0009690.0009225.101∶210.0158630.016363-3.0620.0011750.0011195.0030.0008660.000922-6.07

3 結(jié) 論

通過量綱分析對網(wǎng)殼受頂點沖擊的相似率進行了理論推導(dǎo)，得到考慮應(yīng)變率效應(yīng)的相似律準(zhǔn)則，通過修正模型的沖擊速度，對原型在頂點受沖擊物沖擊的動態(tài)響應(yīng)進行預(yù)測。建立與試驗?zāi)Ｐ拖嗤臄?shù)值模型，對比桿件軸力值和最大接觸力值，驗證有限元分析的可靠性。進行兩例數(shù)值算例分析，分別考慮網(wǎng)殼未破壞和破壞的情況，結(jié)果表明：無論網(wǎng)殼是否破壞，考慮應(yīng)變率效應(yīng)的修正模型在不同幾何縮比下均能較好地預(yù)測原型的豎向位移、應(yīng)力和應(yīng)變等動態(tài)響應(yīng)，具有良好的精度；網(wǎng)殼未破壞時，修正模型可以很好預(yù)測原型接觸力峰值及接觸時間，說明本文得出的相似律準(zhǔn)則是可靠的；未考慮應(yīng)變率效應(yīng)的未修正模型在應(yīng)變率越高、幾何縮比越小時，其預(yù)測誤差越大，且網(wǎng)殼破壞類型越不符合原型。因此，工程應(yīng)用中需考慮應(yīng)變率強化效應(yīng)，利用修正模型試驗可對實際網(wǎng)殼結(jié)構(gòu)受沖擊物沖擊下的動態(tài)響應(yīng)進行預(yù)測。

[1] 李海旺, 郭可, 魏劍偉, 等. 撞擊載荷作用下單層球面網(wǎng)殼動力響應(yīng)模型實驗研究[J]. 爆炸與沖擊,2006,26(1): 39-45. LI Haiwang, GUO Ke, WEI Jianwei, et al. The dynamic response of a single layer reticulated shell to drop hammer impact[J]. Explosion and Shock Waves, 2006, 26(1): 39-45.

[2] 郭可. 單層球面網(wǎng)殼在沖擊載荷作用下的動力響應(yīng)分析[D]. 太原: 太原理工大學(xué), 2004.

[3] WANG Duozhi, ZHI Xudong, FAN Feng, et al. Failure process and energy transmission for single-layer reticulated domes under impact loads[J]. Transactions of Tianjin University, 2008, 14(Sup1): 551-557.

[4] 王多智, 范峰, 支旭東, 等. 沖擊荷載下網(wǎng)殼結(jié)構(gòu)的失效模式及其動力響應(yīng)特性[J]. 工程力學(xué), 2014, 31(5): 180-189. WANG Duozhi, FAN Feng, ZHI Xudong, et al. Failure modes and characteristic of dynamic response for reticulated shells under impact[J]. Engineering Mechanics, 2014, 31(5): 180-189.

[5] 王多智. 沖擊荷載下網(wǎng)殼結(jié)構(gòu)的失效機理研究[D]. 哈爾濱: 哈爾濱工業(yè)大學(xué), 2010.

[6] 吳長. 強震和沖擊荷載下球面網(wǎng)殼的動力失效分析與試驗研究[D]. 蘭州: 蘭州理工大學(xué), 2014.

[7] 談慶明. 量綱分析[M]. 合肥: 中國科學(xué)技術(shù)大學(xué)出版社, 2005.

[8] ALVES M, OSHIRO R E. Scaling impacted structures when the prototype and the model are made of different materials[J]. International Journal of Solid and Structures, 2006, 43(9): 2744-2760.

[9] TRIMINO L F, CRONIN D S. Non-direct similitude technique applied to the dynamic axial impact of bonded crush tubes[J]. International Journal of Impact Engineering, 2014, 64: 39-52.

[10] OSHIRO R E, ALVES M. Scaling of structures subject to impact loads when using a power law constitutive equation[J]. International Journal of Solid and Structures, 2009, 46(18/19): 3412-3421.

[11] DUAN X, SHEPPARD T. The influence of the constitutive equation on the simulation of a hot rolling process[J]. Journal of Materials Processing Technology,2004,150: 100-106.

[12] OSHIRO R E, ALVES M. Scaling of cylindrical shells under axial impact[J]. International Journal of Impact Engineering, 2007, 34: 89-103.

Comparability rule and numerical simulation verificationfor impact dynamic responses of single layer reticulated shells

JIANG Zhengrong1,2, ZHONG Yukai1, SHI Kairong1,2

(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China;2. State Key Laboratory of Subtropical Building Science, South China University of Technology, Guangzhou 510640, China)

Based on the Π principle and considering the strain-rate effect, the condition of similarity for impact response velocities of single layer reticulated shells was corrected to obtain their corrected models. Then, the comparability rule expression for reticulated shells subjected to vertex impact was derived. Using the nonlinear finite element software LS-DYNA, the model described in available literatures was built to verify the reliability of the FE analysis. Then, numerical models of Kiewitt-Lamella single layer reticulated shells were built, these models met the comparability rule with different geometric scalings considering two cases of reticulated shells being damaged and not being damaged. It was demonstrated that the corrected model considering the strain-rate effect can better predict the dynamic responses of the original models; the higher the strain-rate and the smaller the geometric scaling factor, the larger the predicting error with the non-corrected model; the comparability rule considering the strain-rate hardening effect can be applied in practical projects.

single layer reticulated shell; dynamic response; comparability rule; strain-rate effect; numerical simulation

廣州市科技計劃項目(201510010117);華南理工大學(xué)中央高校基本科研業(yè)務(wù)費重點項目(2014ZZ0025)

2015-08-11 修改稿收到日期：2015-10-15

姜正榮 男，博士，副教授，1971年9月

石開榮 男，博士，副教授，1978年8月

O383

A

10.13465/j.cnki.jvs.2016.21.022