基于Popov超穩定理論的實時子結構試驗MRAC控制與仿真

鄧利霞， 范 武

(西南石油大學 土木工程與建筑學院，成都 610500)

?

基于Popov超穩定理論的實時子結構試驗MRAC控制與仿真

鄧利霞， 范 武

(西南石油大學 土木工程與建筑學院，成都 610500)

在實時子結構試驗中，如果加載作動器不能及時、準確、穩定地實現在算法步長內的動作指令或者在加載過程中受到擾動，那么將造成試驗結果的極大失真。為了避免這種情況的出現，創新的將Popov超穩定理論引入到試驗的加載控制中來，設計出了一種MRAC(模型參考自適應控制)系統并通過MATLAB/Simulink進行了建模仿真。仿真結果證明了基于超穩定理論設計的MRAC系統具有良好的跟蹤精度、響應速度和在線糾偏功能，滿足了實時子結構試驗要求。

實時子結構試驗；MRAC系統；加載控制；仿真；超穩定

結構抗震試驗是揭示結構抗震特性的重要手段也是結構抗震設計的基礎。傳統的結構抗震試驗包括擬靜力試驗、擬動力試驗和地震模擬振動臺試驗[1-3]。為了適應結構抗震技術的發展，日本學者基于擬動力試驗的思路提出了實時子結構試驗方法[4]。這種新型的結構抗震試驗方法將結構的關鍵部分作為試驗子結構，進行實時的物理加載，而其余部分作為數值子結構，通過數學模型予以模擬。實時子結構試驗方法既降低了大比例尺抗震結構試驗的成本，又能檢驗速度、加速度相關型結構或構件的性能，綜合了傳統抗震試驗方法的優勢，但同時也面臨許多關鍵的科學問題，吸引了國內外許多學者的關注，得到了較快的發展。

加載控制的穩定性、精度問題和響應速度是實時子結構試驗技術的關鍵問題。模型參考自適應控制系統(MRAC)是一種經典的控制方法，其被運用到涉及控制的各個行業領域。目前結構試驗中大多采用電液伺服系統，對于電液伺服系統，各種機械的，液壓的和電子等非線性集于一體，這種非線性系統如果采用常規的PID控制，很難達到滿意的效果。而MRAC系統在滿足系統精度和響應速度要求的前提下不僅能提高系統的動態性能，還能對系統參數的變化、非線性進行很大程度的適應并能在線糾偏。基于Popov超穩定理論設計的MRAC系統又是全局穩定的，所以能夠滿足試驗加載穩、準、快的目標，提高了試驗的效能。

文獻[5]在試驗中采用了LQR(線性二次最優)控制，在選取合理的增益下才能恰好使作動器完成積分算法步長內的動作指令，如果積分步長選取的比較小，這種控制方法就很難適用了；文獻[6]雖然設計的也是MRAC系統，但其采用的是lyapunov理論。其局限性在于lyapunov函數的尋找比較困難。傳統的PID控制的適應性又很差，而基于Popov理論[7]設計的MRAC系統則成功克服了以上難題。

1 MRAC系統設計

1.1 系統構建

用超穩定理論進行模型參考自適應控制(MRAC)系統設計時，要把被控對象轉化成圖1所示的由兩個方框組成的非線性時變反饋系統，一個方框是處于前饋通道的傳遞函數G(s)，另一個是非線性的反饋回路φ(y,t)。u,y分別為輸入和輸出。

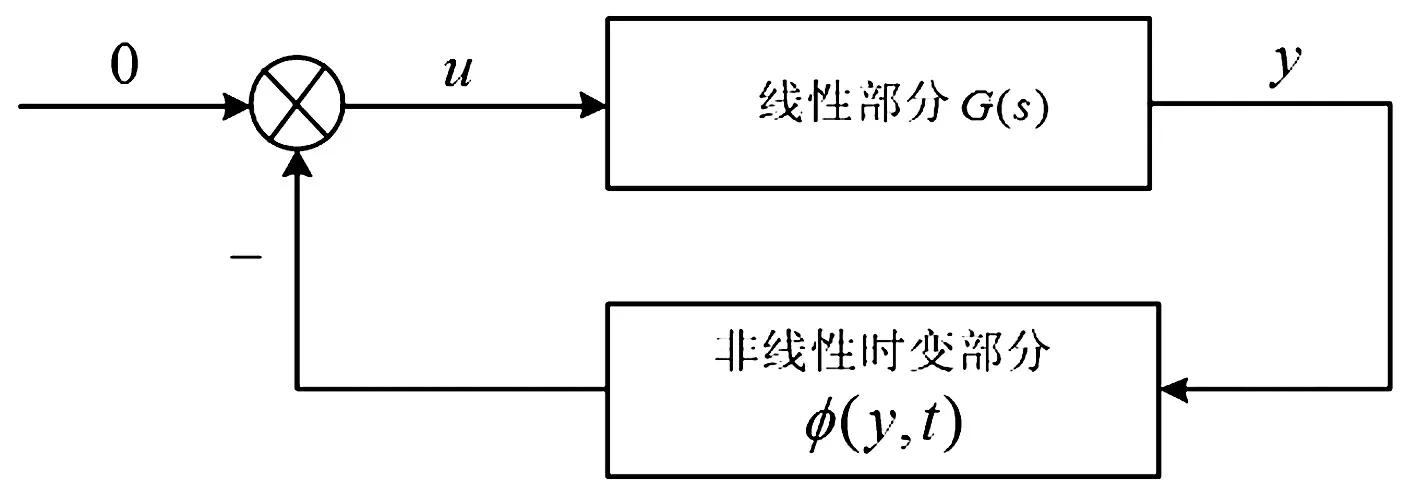
圖1 非線性時變反饋系統Fig.1 The nonlinear time-varying feedback system

參考模型組成線性前向回路，具有時變非線性的被控對象和含有記憶功能的比例積分控制器組成非線性的反饋回路，如圖2所示。其中r為輸入信號,ym和yp分別為參考模型和被控對象的輸出，e為廣義誤差。

圖2 MRAC系統框圖Fig.2 System diagram of MRAC

1.2 自適應規律推導

1.2.1 列數學模型方程

研究對象采用文獻[8]中實驗子結構、作動器及控制器組合系統簡化而成的一個二階傳遞函數

(1)

為了使推導過程簡化，假設參考模型和被控對象的極點相同，但其推導的規律同樣適用極點不同的情況，在后面的仿真證明了這一點。

被控對象的數學模型：

(2)

參考模型的數學模型：

(3)

控制器：

Ge(s)=kc

(4)

廣義誤差：

e=ym-yp

(5)

由圖2知可調系統的傳遞函數為：

(6)

則由式(2)、(3)、(5)得等價的誤差方程：

(s2+a1s+a2)e=(bm-kcbp)r

(7)

1.2.2 求等價非線性反饋系統

對誤差方程做變換得到非線性的反饋系統，其中線性定常部分位于前向通道，非線性時變部分位于反饋通道。根據Popov超穩定理論的要求等價反饋系統必須滿足兩個條件：① 前向通道滿足正實性；② 反饋通道滿足Popov積分不等式。為了滿足前向通道的正實性，需要在前向通道中串入一個補償器D[9],則設計的模型如圖3所示。

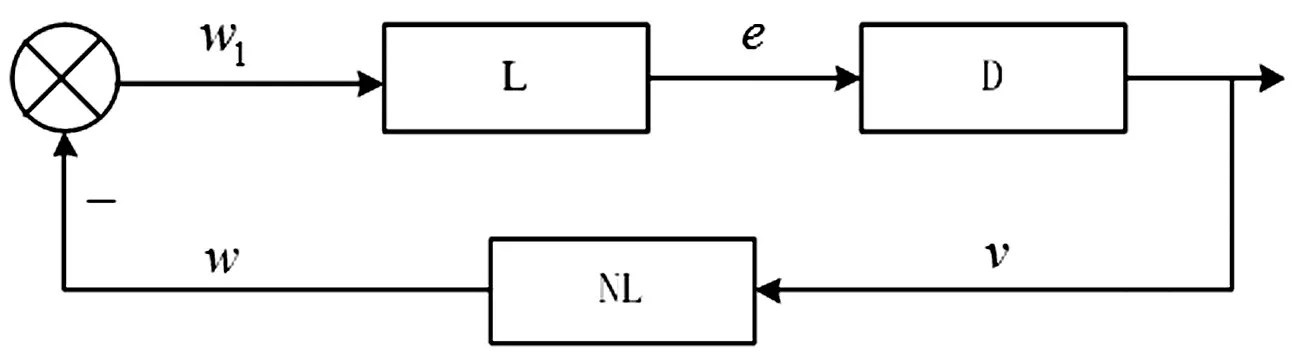
圖3 等價非線性閉環系統Fig.3 Equivalent nonlinear closed loop system

線性塊為：

(s2+a1s+a2)e=w1,w1=-w

(8)

反饋塊為：

w=(kcbp-bm)r

(9)

則線性塊函數(前向通道)：

(10)

為了前向通道的嚴格正實性，串入補償器D，其輸入為e，輸出為v，v=De。其中：

(11)

自適應控制規律的一般形式為：

(12)

為了使反饋塊的輸入、輸出滿足popov積分不等式

(13)

將式(9)代式(13)得：

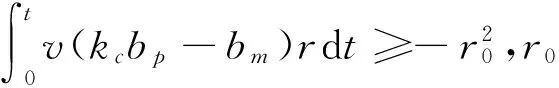
(14)

將式(12)代入式(14)得：

(15)

簡化為：

(16)

(17)

1.2.3 確定D、φ1、φ2，得到自適應律

1.2.3.1 求D

根據Popov定理：前向通道滿足正實性，等價系統的前向通道[10]為：

(18)

其中d0，d1為未知常數

將s=jω代入式(18)，得：

(19)

h(jω)的實部為：

(20)

使Re[h(jω)]>0，需d0>0，d1>d0/a1，串入補償器時只要滿足這兩個不等式即可。

1.2.3.2 求φ1、φ2

由式(16)、式(17)求解φ1、φ2

求φ2：由式(17)取φ2=k2(t)vr，k2(t)≥0，則滿足式(17)。簡單取k2(t)=k2(比例放大系數)得：φ2=k2vr。

求φ1：由微積分

(21)

設f′(t)=vr

(22)

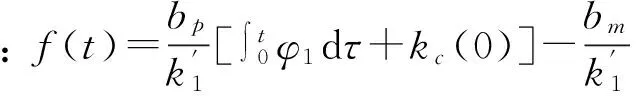
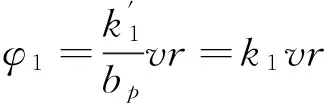
(23)

綜上所述控制器[11-12]：

(24)

2 建模仿真

2.1 動力模型的階躍響應

研究采用式(1)表達的系統二階簡化模型,根據推導出來的補償器D和控制器kc，在Matlab/simulink中建立試驗單步階躍指令仿真系統[13-14]如圖4所示。其中補償器中常數d0、d1需滿足使Re[h(jω)]>0的條件；相應的比例系數k1、k2要滿足φ1、φ2的相應要求。

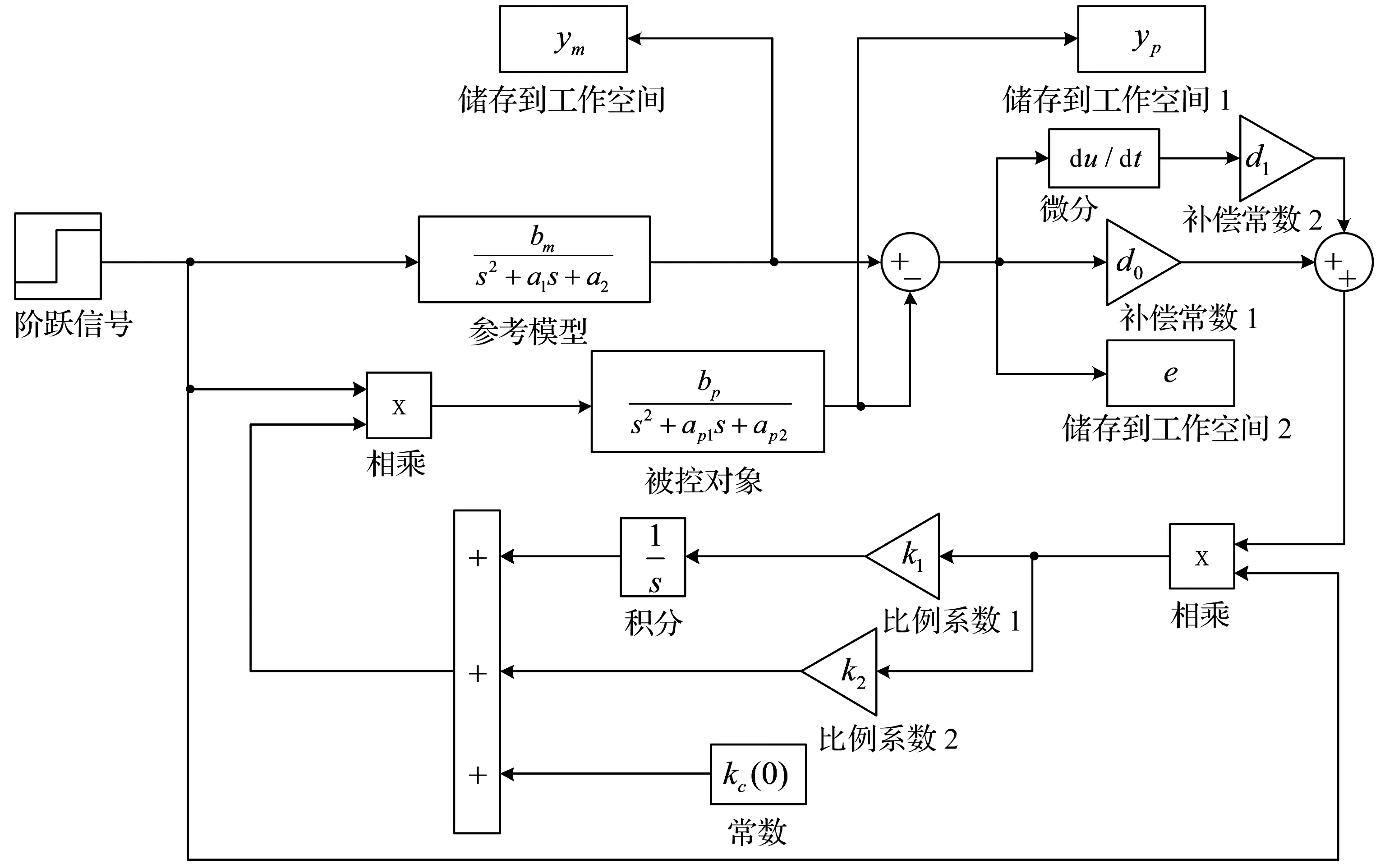
圖4 系統單步控制框圖Fig.4 Step control system diagram

取參考模型參數ξA=1.0,ωA=500,則參考模型的傳遞函數為：

(25)

被控對象參數取bp=20 000，ap1=200，ap2=20 000，系統中串入的補償器參數選取：d0=9.5，d1=0.05，k1=1 500，k2=5.5，kc(0)=0.05，當單位越階指令為0.4 cm、0.6 cm、0.8 cm、1 cm時，則系統的位移響應曲線如圖5所示。

從圖5中的四種位移指令的響應曲線可以看出設計的超穩定MRAC系統的跟蹤性能和穩定性非常好，從數據上分析，在0.015 s以前系統就能完成單步的動作指令，相比文獻[5]的0.04 s要小得多，大大提升了積分算法的步長縮小的空間，有效提升了試驗的精度。從圖形的平滑度可以看出設計的MRAC系統在階躍指令下的動作很穩定。對比幾種位移指令的響應，在調節系數k1，k2確定下來后，位移指令雖然改變，但系統依舊能夠快速、穩定的到達指定位移處，這說明該MRAC調節系統具有很強的的適應性[15]。

為了證明基于超穩定理論設計MRAC系統在實時子結構試驗的加載控制中是一種良好的控制方法，針對試驗子結構簡化的同一被控對象，分別計算出不同剛度(KE[6]和0.1KE)下超穩定MRAC系統、PID控制系統控制下的階躍響應，比較它們的控制效果，結果如圖6所示。從圖中明顯看出超穩定MRAC系統在剛度改變的情況下位移軌跡基本不變， 而PID控制系統則發生不穩

定且不能快速響應位移指令的現象。因此相比PID，超穩定MRAC具有較強的適應性、穩定性和響應快速性。

為了進一步體現超穩定MRAC的優越性，依舊拿同一試驗子結構簡化的被控對象，將其和基于lyapunov的MRAC[6]在同一階躍指令(r=1 cm)的響應下做對比，其中增益參數的選取：超穩定MRAC依舊是上文中選取的k1=1 500，k2=5.5；基于lyapunov的MRAC參數選取為γr=4×105，γy0=4，γy1=0.08。則由兩種控制方法作用下的階躍響應如圖7所示。從圖7可以看出兩種MRAC在響應速度上差別不大，但是在穩定性上基于lyapunov的MRAC在控制沒有達到目標位移時一直在發生輕微的波動，這種波動對試驗來說是不利的，所以超穩定(popov)MRAC在控制的穩定性上優于基于lyapunov的MRAC。

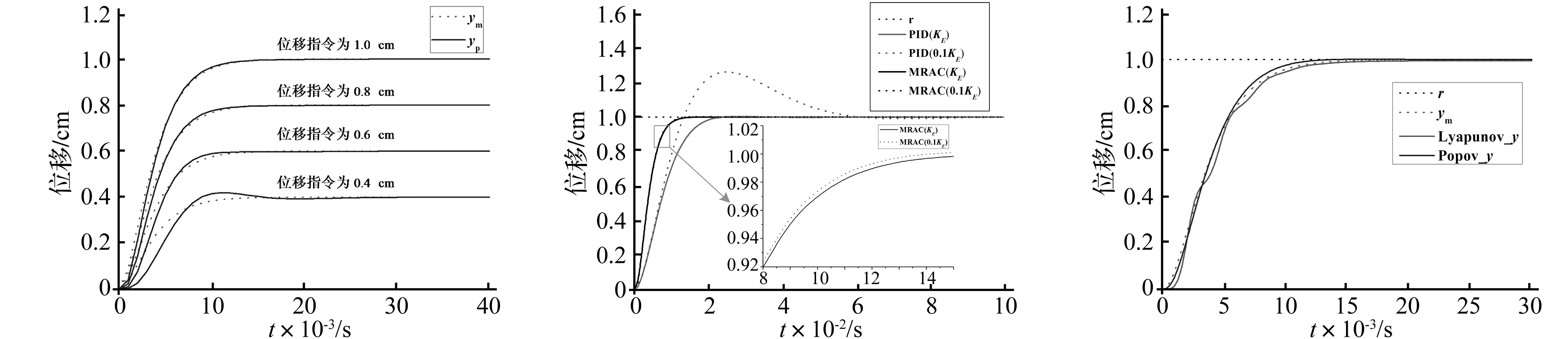
圖5 幾種位移指令下的位移響應Fig.5Displacementresponseofseveralstepinstruction圖6 不同剛度下超穩定MRAC和PID控制的響應Fig.6TheresponseofdifferentrigidityundersuperstabilizationMRACandthePIDcontrol圖7 兩種MRAC的階躍響應Fig.7StepresponseunderthetwokindsofMRAC

綜上所述，在實時子結構試驗的控制加載的階躍響應中超穩定MRAC能夠達到試驗所期望的穩、準、快的目標，其在試驗中的表現要比PID和基于lyapunov的MRAC要好。

2.2 地震作用下的響應

由于研究的是試驗的加載控制采取的都是同一積分算法，所以不考慮數值積分算法的影響。在實時子結構試驗中，數值子結構在離散時域上的運動方程可以寫成如下形式[16]：

MNaN,i+CNvN,i+KNdN,i+RE,i=Fi

(26)

式中:M、C及K分別為數值子結構的質量、阻尼及剛度矩陣；ai、vi及di為第i步的加速度、速度及位移向量；R為反力向量；F為結構所受的外荷載向量；下標N和E分別表示數值子結構和試驗子結構。根據標準中心差分法[17]的假定可知數值子結構的速度和加速度分別為

(27)

(28)

式中:Δt為積分時間步長。將式(27)與式(28)代入式(26)，整理后可以得到

(29)

試件為動力子結構，因此上式中的反力RE,i與試驗子結構第i步實現的位移、速度和加速度相關，為了保證測得的RE,i盡量準確，加載裝置需要帶動試件實現的除了位移dE,i外，還有速度vE,i和加速度aE,i。所以加載控制系統在Δt內穩定、精確的實現相應的指令對試驗十分重要。試驗原理圖如圖8所示。

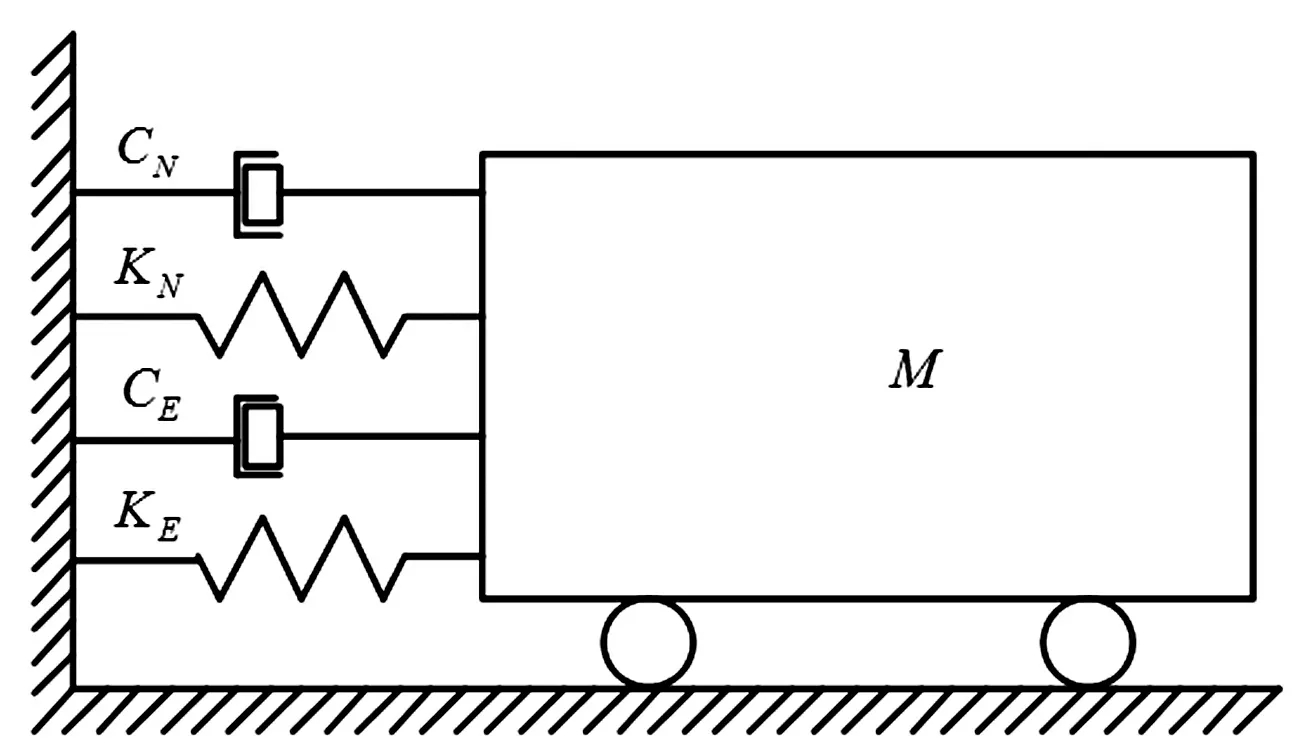
圖8 單自由度實時子結構試驗原理圖Fig.8 Schematic diagram of real-time substructure testing with one degree

對于單自由度實時子結構試驗體系，M=5 000 kg；KN=147.392 kN/m、CN=3.143 2 kNs/m分別為數值子結構的剛度系數和阻尼系數；KE=50～2 000 kN/m,CE=4.2 kNs/m分別為實驗子結構的剛度系數和阻尼系數。結構的初始位移、初始速度和初始加速度均為零。仿真輸入荷載為El Centro(NS,1940)地震波，峰值加速度調整為0.02 g，積分步長為Δt=0.04 s。調整系數k1=5 500,k2=15,在MATLAB/Simulink中進行仿真結果如圖9所示，其中精確解是通過微分求解器(MATLAB中的LSIM命令)求得的。

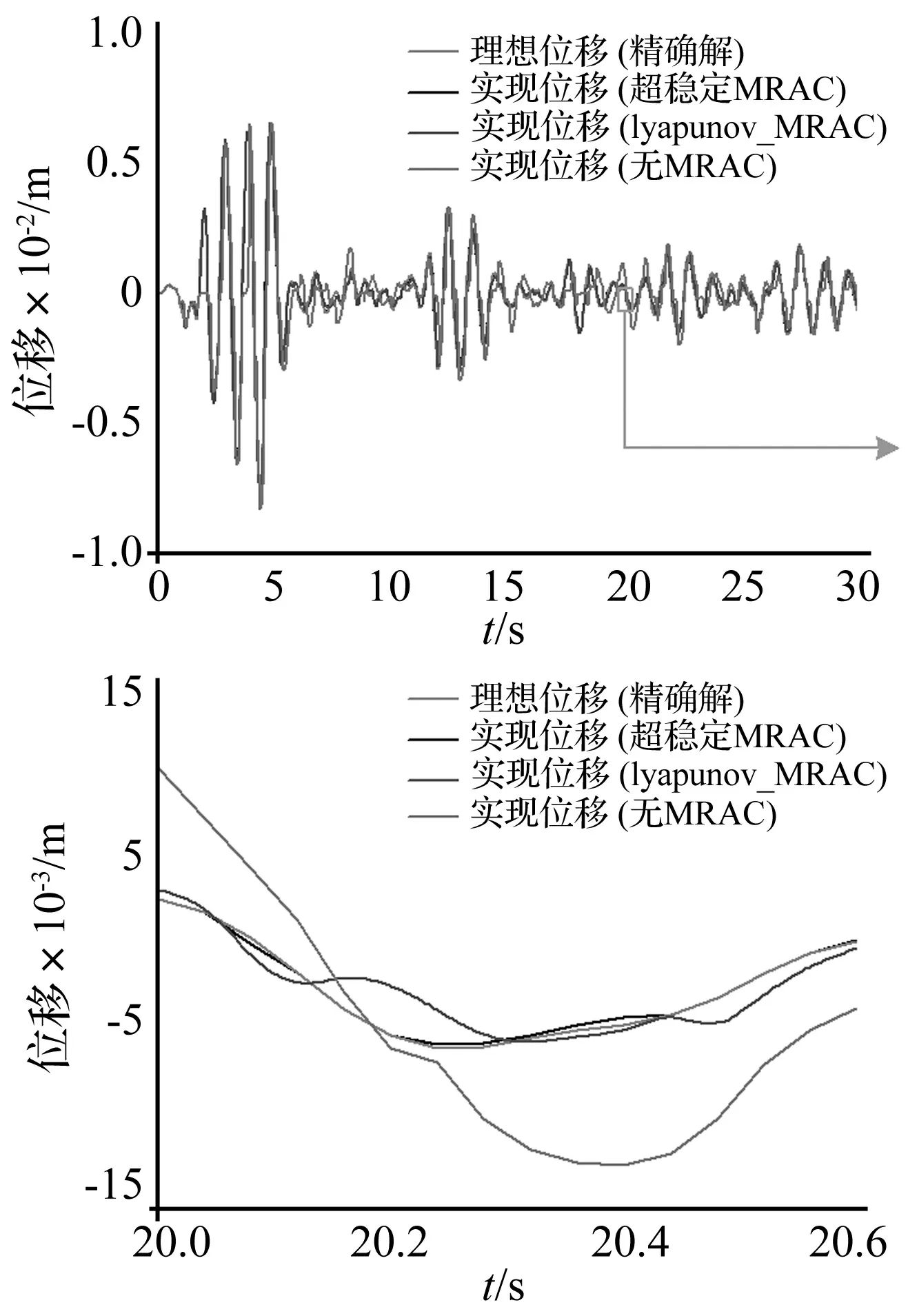
圖9 超穩定MRAC控制下的仿真結果和精確解的對比Fig.9 The comparison between exact solution and the simulation’s result by Super stable MRAC

從圖9中的仿真結果可以看出，超穩定MRAC、lyapunov_MRAC以及無MRAC和精確解四條位移曲線的走勢中，超穩定MRAC和精確解的吻合程度最高，幾乎完全重合，這種結果證明了基于Popov理論的MRAC系統可以很好的保證試驗的精度和穩定性，從而可以提高試驗結構的可靠性，使其更能反映結構的動力特性，從而為抗震設計提供依據。

3 結 論

基于Popov超穩定理論設計的MRAC系統在實時子結構加載控制中對指令的響應及時、穩定、精準，是一種較為優秀的控制系統，可以在試驗中應用并推廣。但本文得到的推導規律和應用仿真都是比較簡單的，很多地方還是有待完善的，如比例系數的選取范圍、改變系數對試驗結果的影響以及高階作動器控制律的推導等，這些都有待進一步繼續研究。

[1] 邱法維，錢稼茹，陳志鵬. 結構抗震試驗方法[M]. 北京：科學出版社，2000.

[2] 何文福，劉文光，張穎,等. 高層隔震結構地震反應振動臺試驗分析[J]. 振動與沖擊，2008，27(8): 97-101. HE Wenfu, LIU Wenguang, ZHANG Ying, et al. High-rise structure seismic response analysis of vibration table test[J]. Journal of Vibration and Shock, 2008，27(8): 97-101.

[3] 韓強，杜修力，劉晶波,等. 多維地震作用下隔震橋梁地震反應(I)一模型結構振動臺試驗[J].振動與沖擊，2008，27(9): 59-65. HAN Qiang, DU Xiuli, LIU Jingbo, et al. Isolation bridge seismic response under multi-dimensional earthquake(I)—model structure of shaking table test[J]. Journal of Vibration and Shock, 2008，27(9): 59-65.

[4] TAKNASHI K, NAKASHIMA M. Japanese activities on on-line testing, journal of engineering mechanics, ASCE, 1987, 113(7): 1014-1032.

[5] 張濤. 電液伺服加載系統的LQR控制及在實時子結構實驗中的應用[D]. 哈爾濱：哈爾濱工業大學, 2008.

[6] 鄧利霞. 實時子結構實驗的自適應控制方法[D]. 哈爾濱：哈爾濱工業大學,2007.

[7] POPOV V M. Hyperstability of contorl systems. Spring Verlag, 1973

[8] 王倩穎. 實時子結構試驗方法及其應用[D]. 哈爾濱：哈爾濱工業大學,2007.

[9] lANDAU I D. Ahyperstablility criterion for model reference adaptive control systems [J]. IEEE Trans. Autom. control,1969:552-555.

[10] LI Y, ZHANG K, WANG H. Aadaptive contorl theory and appliction[M]. Xi An：Northwestern Polytechnical University press, 2010:81-83.

[11] 陳復揚,姜斌.自適應控制與應用[M].北京：國防工業出版社，2009:111-121.

[12] 韓彥彬. 正定積分算子的本征值[J]. 河北大學學報(自然科學版),1986,1:18-30. HAN Yanbin. The eigenvalues of positive definite integral operator [J]. Journal of Hebei University (Natural Science Edition),1986,1:18-30.

[13] 王正林. MATLAB/Simulink與控制系統仿真[M].北京：電子工業出版社，2012.

[14] 石良臣. MATLAB/Simulink系統仿真超級學習手冊[M].北京：人民郵電出版社，2014.

[15] LANDAU I D. A survey of model reference adaptive techniques—Theory and applications [J]. Automatica，1974,10(4):353-379.

[16] WU B, BAO H, OU J, et al. Stability and accuracy analysis of central difference method for real-time substructure testing[J]. Earthquake Engineering and Structural Dynamics,2005, 34: 705-718.

[17] WU B, DENG L, YANG X. Stability of central difference method for dynamic real-time substructure testing[J]. Earthquake Engineering and Structural Dynamics,2009, 38: 1649-1663.

MRAC control and simulation for real-time substructure testing based on Popov hyperstability theory

DENG Lixia, FAN Wu

(School of Civil Engineering and Architecture, Southwest Petroleum University, Chengdu 610500, China)

In real-time substructure testing, if the loading actuator cannot achieve action commands in time and correctly in an algorithm step or is disturbed in a loading process, it may cause a great distortion of test results. In order to avoid the occurrence of such a situation, Popov super stability theory was introduced into the loading control of tests. A model reference adaptive control(MRAC)system was designed and with MATLAB/Simulink, its modeling and simulation were conducted. The simulation results showed that the MRAC system designed using the super stabilitr theory has better tracking accuracy, response speed and online error-correcting function to meet the requirements of real-time substructure testing.

real-time substructure testing; MRAC system; load control; simulation; hyperstability

西南石油大學青年教師“學術過關”項目(201131010078)

2015-06-10 修改稿收到日期：2015-10-23

鄧利霞 女，講師，博士，1978年生

TU317.1;TU311.3

A

10.13465/j.cnki.jvs.2016.21.007