Palmer線性化定理的一個改進

申艷楓

(浙江師范大學 數理與信息工程學院，浙江 金華321004)

?

Palmer線性化定理的一個改進

申艷楓

(浙江師范大學 數理與信息工程學院，浙江 金華321004)

改進了Palmer線性化定理，減弱了原來Palmer線性化定理的條件.

部分指數型二分性；線性系統；拓撲等價

0 引 言

考慮非自治微分方程

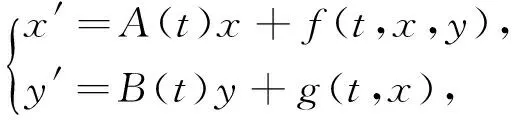
(1)

我們假設

|U(t)U-1(s)|< kexp-α(t -s) (t ≥s)

(2)

(3)

這里k,α都是大于零的常數．

當線性部分具有指數型二分性時，已經有許多學者討論了其線性化的問題[1-18].1973年,K.J.Palmer將Hartman定理推廣到非自治系統[1-2]．此外，林發興，史金麟教授等也研究了x′=A(t)x，y′=B(t)y部分具有指數型二分性條件下線性化定理[3-9]，但是史金麟教授只討論了

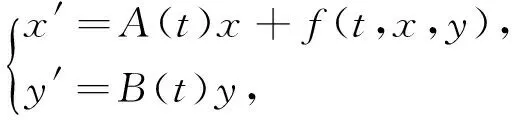
(4)

當y′=B(t)y沒有線性項時的線性化．所以本文討論

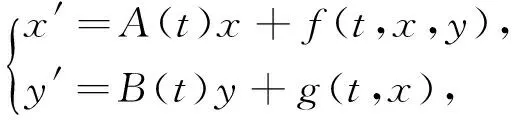
(5)

其中y′=B(t)y有線性項g(t，x)時的線性化．

1 主要定理

定理1 設(2)，(3)式成立，又設對任意x1，x2∈n1，y1，y2∈n2，t∈有

(6)

(7)

(8)

(9)

這里μ，γ，M是大于零的常數，若

2kγ<α

(10)

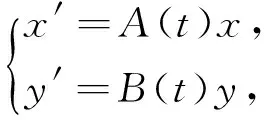
(11)

的解．

(ⅱ)當x→∞，H(t，x)→∞一致的成立．

(ⅲ)設H-1(t，·)=G(t，·)，則v→∞,G(t，v)→∞一致地成立．

(ⅳ)設u(t)是系統(1)的解，則H(t，u(t))是系統(9)的解，v(t)是系統(9)的解，則G(t，v(t))是系統(1)的解．

定理的證明關鍵是構造同胚函數．首先證明一些引理．

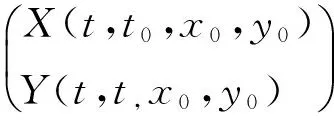
引理1 對任意固定的(τ，ζ，η)，系統

Z′=A(t)Z-f(t,X(t,τ,ζ,η),Y(t,τ,ζ,η))

(12)

有惟一有界解h(t，(τ，ξ，η)，且|h(t，(τ，ξ，η))|≤kμα-1.

證明 對任意給定的(τ，ξ，η)取

直接微分上式易證Z0(t)是(10)的一個解．利用條件(2)，(4)可得

所以Z0(t)是(10)的有界解．由于對于給定的(τ，ξ，η)，系統(10)是線性非齊次系統．線性部分Z′=A(t)Z由于具有指數型二分性，所以除零解以外沒有其他有界解．因此(10)的有界解是惟一的．這個有界解自然與(τ，ξ，η)有關，因此可記為h(t，(γ，ξ，η))，且|h(t，(γ，ξ，η))|≤kμα-1，證畢．

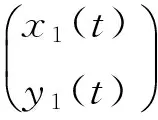
Z′=A(t)Z+f(t,x1(t)+Z,y1(t))-f(t,x1(t)+Z,y1(t))

(13)

有惟一的有界解Z=0．

證明 顯然Z=0是系統(12)的一個有界解．現在證明有界解的惟一性．設Z1(t)是系統(12)的一個有界解，則

同引理1的推理可得

又根據條件(2)，(6)，(8)可得

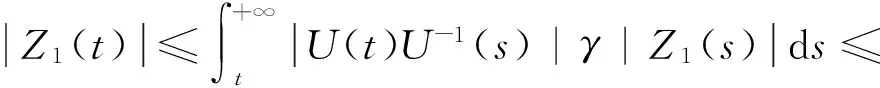
從而可得Z1(t)=0．證畢．

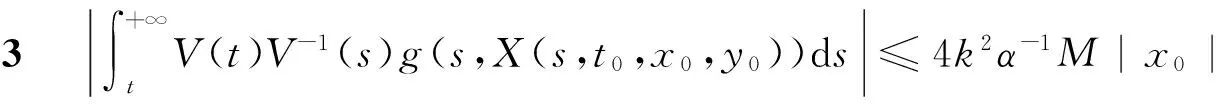
證明 設

我們可以證明

(14)

(15)

(16)

又由(12)，(14)可得

現在引進函數

H1(t,x,y)=x+h(t,(t,x,y))

(17)

(18)

(19)

(20)

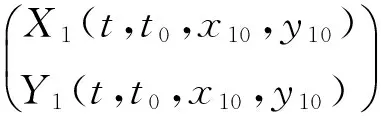
證明 由于用(t，X1(t，τ，ξ，η)，Y1(t，τ，ξ，η))代替系統(10)中的(τ，ξ，η)，系統(10)不會發生任何變化，

所以有

h(t,(t,X1(t,τ,ξ,η),Y1(t,τ,ξ,η)))=h(t,t0,x10,y10)

H1=(t,(t,X1(t,t0,x10,y10),X2(t,t0,x10,y10))=X1(t,t0,x10,y10)+h(t,(t0,x10,y10)))

H2(t,X1(t,t0,x10,y10),X2(t,t0,x10,y10))=X2(t,t0,x10,y10)+

上式左端記為H1(t)，微分上式得

H1(t)′=A(t)X1(t,t0,x10,y10)+f(t,X1(t,t0,x10,y10),Y1(t,t0,x10,y10))+

A(t)h(t,(t0,x10,y10))-f(t,X1(t,t0,x10,y10),X2(t,t0,x10,y10))=A(t)H1(t)

H2(t)′=B(t)Y2(t,t0,x10,y10)+g(t,X1(t,t0,x10,y10))+

證明

(t,Y1(t,t0,y10,y20),Y2(t,t0,y10,y20)),G2(t,Y1(t,t0,y10,y20),Y2(t,t0,y10,y20))))ds

將上式左端記為G1(t)，微分上式得

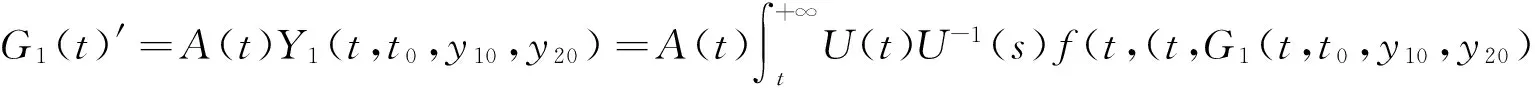
Y2(t,t0,y10,y20)),G2(t,Y1(t,t0,y10,y20),Y2(t,t0,y10,y20))))ds+

f(t,(t,G1(t,Y1(t,t0,y10,y20),Y2(t,t0,y10,y20)),G2(t,Y1(t,t0,y10,y20),

Y2(t,t0,y10,y20))))ds=A(t)G1(t)+f(t,G1(t),G2(t))

G2=(t,Y1(t,t0,y10,y20),Y2(t,t0,y10,y20))=Y2(t,t0,y10,y20)-

將上式左端記為G2(t)，微分上式得

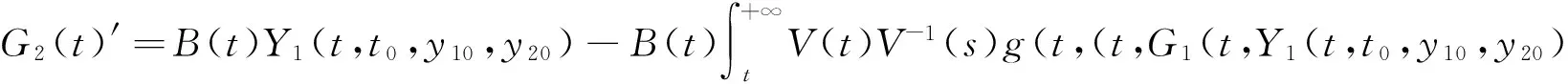
Y2(t,t0,y10,y20)))ds+g(t,(t,G1(t,Y1(t,t0,y10,y20),Y2(t,t0,y10,y20)))=

B(t)G2(t)+g(t,G1(t))

引理5 對于任意y1∈n1,y2∈n2,t∈恒有

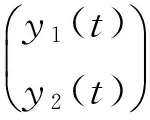
是系統(1)的一個解．又由引理(4)

所以J(t)是Z′=A(t)Z的一個解．由引理3可得

|J(t)|=|H1(t,G1(t,y1(t),y2(t)),G2(t,y1(t),y2(t)))-y1(t)|≤

|H1(t,G1(t,y1(t),y2(t)),G2(t,y1(t),y2(t)))-G1(t,y1(t),y2(t))|+

|G1(t,y1(t),y2(t))-y1(t)|≤2kμα-1+2kμα-1=4kμα-1

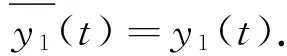
此外

H2(t,G1(t,y1(t),y2(t)),G2(t,y1(t),y2(t)))-y2(t)=G2(t,y1(t),y2(t))+

所以H2(t，G1(t，y1(t)，y2(t))，G2(t，y1(t)，y2(t)))=y2(t)，綜上引理得證．

引理6 對于任意x1∈n1,x2∈n2，t∈恒有

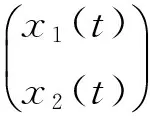
是系統(9)的一個解．又由引理(5)

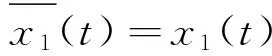
另外

G2(t,H1(t,x1(t),x2(t)),H2(t,x1(t),x2(t)))-x2(t)=H2(t,x1(t),x2(t))-

所以G2(t，H1(t，x1(t)，x2(t))，H2(t，x1(t),x2(t)))=x2(t)，綜上引理得證．

所以J(t)是Z′=A(t)Z的一個解．由引理3可得

|J(t)|=|H1(t,G1(t,y1(t),y2(t)),G2(t,y1(t),y2(t)))-y1(t)|≤

|H1(t,G1(t,y1(t),y2(t)),G2(t,y1(t),y2(t)))-G1(t,y1(t),y2(t))|+

|G1(t,y1(t),y2(t))-y1(t)|≤2kμα-1+2kμα-1=4kμα-1

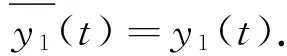
此外

H2(t,G1(t,y1(t),y2(t)),G2(t,y1(t),y2(t)))-y2(t)=G2(t,y1(t),y2(t))+

所以H2(t，G1(t，y1(t)，y2(t))，G2(t，y1(t)，y2(t)))=y2(t)，綜上引理得證．

驗證(ⅰ)由引理5與引理6可推知，對任意固定的t，H(t，·)是雙射，且H-1(t，·)=G(t，·)．

驗證(ⅱ)由引理1和引理3得|H1(t，x)-x|=|h(t，(t，x))|≤kα-1μ．所以當x→∞時H1(t，x)→∞與H2(t，x)→∞，且均關于t是一致的，所以H(t，x)是一致連續函數．

驗證(ⅲ)由引理1和引理3得，當y→∞時G1(t，y)→∞與G2(t，y)→∞,且均關于t是一致的．所以G(t，y)是一致連續函數．

驗證(ⅳ)由引理4和引理5立得．

由上所述，系統(1)拓撲等價于(9)，定義證畢．

[1]Plamer K J.A characterization of exponential dichotomy in terms of topological equivalence[J]. Jour. Math. Anal.,1979,69:8-16.

[2]Plamer K J. A generalization of Hartman,s linearization theorem[J]. Jour. Math. Anal.,Appl.,1973，41:753-758.

[3]史金麟．微分方程分類原理[M].北京：科學出版社,1999: 111-125.

[4]史金麟．Hartman線性化定理的改進[J]．中國科學(A輯)，2002，32:458-470.

[5]史金麟．Hartman定理在臨界性的推廣[J].南開系列，純粹應用數學與理論物理,4:67-89.

[6]史金麟．臨界情形下的全局拓撲線性化[J]．數學學報，2001，44:1019-1026.

[7]Lin MR. Generalized exponential dichotomy[J].J.-Vuzhou Un,iv.(Nat. Sic).Edition,1982,10(4):21-30.(in Chinese)

[8]江良平．Palmer線性化定理的一個推廣[J].應用數學，2011，24(1): 150-157.

[9]林發興．線性系統指數型二分性[M].合肥：安徽大學出版社,1999: 17-71.

[10]Lin F X. The existence on periodic solutions and almost periodic solutions of lienard equa-tion[J],Acta Math. Sci.,2003,3:643 -662.

[11] Lin F X Exponential Dichotomies of Linear Systems[M].Anwei University Press,Hefei,1999.(in Chinese).

[12]林木仁．廣義指數型二分性等價條件[J].福州大學學報(自然科學版)，2002,30(2): 158-162.

[13] Coppel WA. Dichotomies in Stability Theory[M].Springer-Verlag,Berlin,1978.

[14] Pinto M. Dichotomy and existence of periodic solutions of quasilinear functional differential equations[J].Non,lin,ear A’nat.,2013,400(2):1227-1234.

[15] Xia Y H,Chen X,Romanovski V. On the Linearization Theorem of Fenner and Pinto[J].J. Math.Anal.Appl.,2013,400(2):439-451.

[16] Xia Y H,Li J,Wong PJY. On the topological classification of dynamic equations on time scales[J].Non,lin.ear Afnal.: Real Wortd Appl.,2013,14(6):2231-2248.

[17] Palmer K J.A characterization of exponential dichotomy in terms of topological equivalence[J]. J.Math.Anal.Appl.,1979,69:8-16.

[18] Palmer K J. The structurally stable linear systems on the half-line are those with exponential dichotomies[J].J.Difj.Equ.,1979,33:16-25.

[19] Reinfelds A.A generalized theorem of Grobman and Hartman[J].Latv. Mat.Ezheg.,1985,29: 84-88.

[20] Naulin R.A remark on exponential dichotomies[J],Revista Colom.Math.,1999,33:9-13.

[21] Minh N Van. On the proof of characterizations of the exponential dichotomy[J]. Proc.Amer.Math.Soc.,1999,127:779-782.

[22]萎風華．泛函微分方程的Lipschitz穩定性[J].浙江師范大學學報(自然科學版),2004(04):338-341.

[23]盛廷贊．一類混合型泛函微分方程的柯西問題[J].浙江師范大學學報(自然科學版),1997(03):12-14.

[24] Ngoc PHA,Natio T. New characterizations of exponential dichotomy and exponential sta-bility of linear difference equations[J].J.Diff.Equ.Appl.,2005,11:909-918.

[25] Petre A P,Megan M. On uniform exponential dichotomy of linear skew-product three-parameter semiflows in Banach spaces[J].Rornai J.,2011,7(1):7.

[26] Sacker R,Sell G. Dichotomies for linear evolutionary equations in Banach spaces[J].J.Dzj-f.Equ.,1994,113:17-67.

[27] Jiang L.A generalization of Palmer’s linearization theorem[J].Appt.Math.,2011,24:150-157.(in Chinese)

[28] Jiang L. Generalized exponential dichotomy and global linearization[J].J.Math.AnaI.Appt.,2006,315:474-490.

[29] Jiang L.,Strongly topological linearization with generalized expoential dichotomy[J],Non-l.Anal. TMA.,2007,67:1102-1110.

[責任編輯：王軍]

The improvement of Palmer linearization theorem

SHEN Yanfeng

(School of Mathematics and Information Engineering,Zhejiang Normal University,Jinhua 321004,China)

This paper improved the Palmer linearization theorem. We reduced the conditions in Palmer linearization theorem to more conservative conditions.

exponential dichotomy; linear system; topological equivalence

2016-03-17

浙江省自然科學基金(LY15A010022)資助項目

申艷楓(1991—)，女，河北承德人，浙江師范大學碩士生，主要從事常微分方程與動力系統的研究.

O241

A

1672-3600(2016)12-0016-06