均值不等式的研究

山東省廣饒縣第一中學　　孟　　偉

均值不等式的研究

山東省廣饒縣第一中學孟偉

這個看似復雜的題實際上用n個二元均值不等式就可以解決，其中用到的手法就是局部分析處理，難題就是一些簡單事實的羅列.

高中數(shù)學不等式均值

在不等式中，常常遇到n個變元的問題.這時，常用的手法是拿出一個或兩個變元單獨處理，解決局部問題從而達到解決整體問題的目的.

例1設x1，x2，……，xn都是正數(shù).證明

最自然的想法是證明左邊的每一個式子都分別大于等于右邊的每一個式子即可.由均值不等式，……可類似的得到n個式子，將上式疊加，即得

再移項，即證題中不等式.這個看似復雜的題實際上用n個二元均值不等式就可以解決，其中用到的手法就是局部分析處理，難題就是一些簡單事實的羅列.

在證明不等式時，比如要證x1+x2+……+xn≤0，可以證每個變量小于等于0或使其小于等于多個易于求和的式子，使這些式子相加為0即可達到證明.

例2設x1，x2，x3〉0，證明

有時在證明不等式的問題中，我們常常先找出不等式等號成立的條件，從而進一步證明.

我們發(fā)現(xiàn)x1=4x2=16x3時，等號成立.

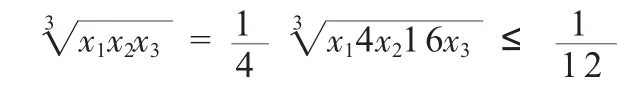
在其他的一些用均值不等式證明的題中，有時還需構(gòu)造的技巧，適當添加項.比如在用n元均值不等式時，可構(gòu)造出n個式子，再利用不等式.

由以上的兩個題可看出，局部分析可有力地解決整體問題.微積分是現(xiàn)代數(shù)學的一個重要分支，就是從微觀的角度來解決問題.一般只有從微觀上可反映問題的本質(zhì)，整體問題用局部分析的方式解決.這本身就體現(xiàn)一種思想，非常重要的思想.