淺談初中數學教學中如何創設問題情境

張明媚

（播州區團溪鎮中學 貴州遵義 563131）

淺談初中數學教學中如何創設問題情境

張明媚

（播州區團溪鎮中學 貴州遵義 563131）

在數學教學中，培養學生的思維能力需要創設問題情境，即利用和現實生活中的現象類比的方法創設問題情境；對老問題進行延伸創設問題情境；利用數學建模的方法創設問題情境；利用聯想來創設問題情境；利用簡單的數學實驗來創設問題情境；利用數學材料創設問題情境；利用數學故事、典故來創設問題情境。

數學教學 問題情境 方法

近年來，我們在各級領導的組織指導下，進行數學教學中創設問題情境的方法的探索，通過互聽探索公開課，聽后進行講座和總結的方法來研究。通過教學實踐的探索、檢驗探索的效果，最后總結出以下方法：

一、利用和現實生活中的現象類比的方法創設問題情境

學生的絕大部分時間都在生活，認識最牢靠和最根深蒂固的部分就是生活中經常接觸和經常用的知識。有些已經進入他們的潛意識，如果教學中能運用這些知識做類比，那么將是非常受學生歡迎的，一旦接受也會被學生牢牢的掌握，而現代的教學手段很容易讓現實生活中的現象再現或模擬于課堂之上。

例如：在整式同類項的教學中，我們可以和實際中的例子相比較，把數學分類的思想形象化，在電化教室對一群豬羊的圖片進行分類，分類的方法：無角的是豬，有角的是羊。這基本就是一個游戲，每個同學都可以輕而易舉的做到，對于七年級的同學，還感到新奇以至于達到情緒高漲，這時抓住時機自然的過渡到同類項的分類中來，分類的方法：字母相同，相同字母的指數相同；學生乘勝追擊，很自然的應用剛剛在豬羊分類中形成的程序，先看字母，再看字母的指數。

即：豬羊的分類（按外部形態） 多項式的分類（按字母和字母的指數）

在初二根式的加減運算中也可以做這樣的比喻，實際上他們和合并同類項是一樣的，這樣不僅降低了問題的難度并且加深了學生對問題的理解，同時讓學生接觸了數學分類的思想。

二、對老問題進行延伸創設問題情境

解決問題和一個人的知識水平、認知結構等有關。作為教師如果能貼切的了解 學生的知識水平、認知結構，并適當的發展他，不僅能夠完成教學任務，而且能夠深化這種結構，使學生如何學習，并且大膽的發現問題、提出問題。例如：在七年級的幾何開始部分有這樣一道題：

在等腰三角形ABC中，∠A=30o，又CT平分∠ACB，求ATC的度數。

這是一道基本考察了學生等腰三角形、角平分線以及三角形內角和的概念，如果僅僅讓學生解決這道問題。教學就有些平淡了，如果在解決了這道問題之后，再向深處挖掘，進一步深化學生認知結構，將是非常有益的；我進一步提出了如下的問題：對于∠A=x度，你能用含x的代數式表示∠ATC嗎？這看上去是一小步，僅僅是把30度換成了x0，數字換成了字母，實際上卻是一大步，它鞏固了前面的多項式，也和函數有了聯系。當問題解決了，我再緊追一問：當x等于多少時，∠ATC=50o？這就成了一個方程問題，這就充分利用了前面的問題情境。不僅鞏固知識，也發展了知識，對于學生發問，思考都是有利的。

要把學生從題海中解放出來，就需要我們老師精選習題 ，要題盡其用，通過習題最大的鍛煉學生的思維能力和對知識的把握能力。

三、利用聯想來創設問題情境

在初中數學教學中，一題多解、多題一解的現象是很普遍的。讓學生較多的接觸，適當的總結，是有利于學生發散思維能力的提高。匈牙利數學教育家、喬治·波利亞在《怎樣解題》中指出：“要聯想有沒有做過類似的題目，有沒有做過條件相似的題目。有沒有做過結論相似的題目。”例如：在作好了這樣一道題目后：線段AB中點為D，若線段BD的長度為5cm，那么線段AB的長度是多少？我再給學生提出這樣的問題：已知∠AOB的角平分線為OC，∠AOC的角平分線為OD，若∠COD的度數為500，那么∠AOB的度數是多少？這兩道題目的考察角度不同，但方法完全一樣，對于低年級的同學學習幾何問題是很好的。利用聯想來創設情境的關鍵是要找出問題相似的地方，及“形似”（條件或結論一樣），“神似”（方法或解題的思路一樣）。“形似”我們稱之為一題多變，而“神似”我們稱之多題一解。

五、利用簡單的數學實驗來創設問題情境

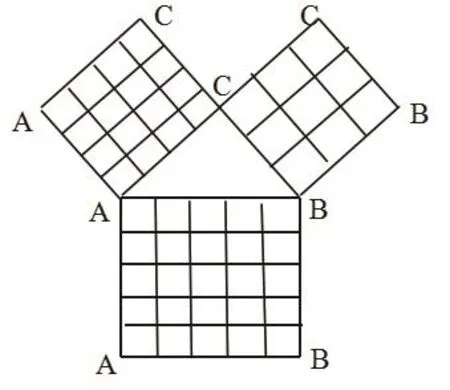
利用數學實驗的方法來創設問題的情境在低年級的實驗幾何階段是很平常的事情，先讓學生觀察實驗，然后總結得到數學結論，如求圓柱的體積，采用了把圓柱進行分割，拼成一個近似的長方體，分得越多，越接近一個長方體，讓學生觀察兩者之間的關系，從而得到長方體的體積公式。在初中的高年級，數學實驗幾乎為零，但我們可以通過數學軟件來模擬實驗的過程，例如講解勾股定理時，讓學生通過觀察不同的直角三角形三邊平方的關系來得到勾股定理：如圖所示。

三個正方形面積分別代表了三邊的平方。定義一個小正方體面積為1個面積單位，通過查正方體的個數就可以得到三邊平方的關系了。

《幾何畫板》可以演示較多的數學實驗特別是幾何中數量關系。

六、利用數學材料創設問題情境

數學中，通過觀察材料，觀察方法，觀察思路來啟發學生思考得到新的結論，這類方法更適合開放型題目的設置，更容易讓學生發揮發散性思維。

可以觀察到，被減數與減數的分子都是1，分母是相鄰的兩個正整數時，差的分母是兩個相鄰自然數的積。

學生的視角不同，得到的結論既不同。針對上面的問題，在老師的啟發下，學生互相啟發，也就得到了更多的結論。如：（n為正整數），學生通過觀察歸納：兩個加數的分子為1，分母是相鄰的兩個正整數時，和的分母是這兩個正整數的積，分子是較小整數的2倍加1。

七、利用數學故事，數學典故來創設問題情境

數學故事、 數學典故有時反映了知識形成的過程，有時反映了知識點的本質，用這樣的故事來創設情境不僅能夠加深學生對知識的理解，還能加深學生對數學的興趣，提高數學的審美能力。例如：在講解平面直角坐標系的過程中，我們可以先見解數學家歐拉發明坐標系的過程，躺在床上靜靜地思考如何確定事物的位置，這時發現蒼蠅粘在了蜘蛛網上，蜘蛛迅速地爬過去把它捉住。歐拉恍然大悟：“啊，可以像蜘蛛一樣用網格來確定事物的位置啊。”引入正題，怎樣用網格來表示位置。這時學生的興致已經調動起來了。

綜上所述，數學教學是一個系統工程，培養學生的能力是最終目的，而創設問題情境只是一個手段，創設問題情境的方法也決不僅僅這幾種，他需要我們不斷的探索和自身知識的不斷豐富，需要我們對生活的熱愛和對教育的熱情。