高中數學教學中如何培養學生的方程思想初探

白玉花

（吉林省汪清縣汪清二中學 吉林延邊 133200）

高中數學教學中如何培養學生的方程思想初探

白玉花

（吉林省汪清縣汪清二中學 吉林延邊 133200）

方程思想是高中數學教學中一種重要的解題應用方法，也是高考重點考察的數學思想之一。方程思想是學習函數知識的基礎，方程思想是通過設元，探求已知與未知之間的等量關系，構造方程或方程組，然后求解方程完成未知向已知的轉化，這種思想對于高中數學學習具有重要意義。基于此，筆者結合案例，試在文章中探討在高中數學教學中的應用，旨在培養高中生的方程思想，促進高中數學教學質量的提升。

高中數學 方程思想 培養

引言

方程思想在高中數學教學中的應用很廣泛，也是高考數學考試中的熱點。函數思想與方程思想的聯系十分密切，教師在滲透方程思想的過程中，不可避免的要和函數思想有所結合。解方程如分f（x）=0，就是求函數y= f（x）當函數值為零時自變量x的值；求綜合方程f（x）= g（x）的根或根的個數，就是求函數f（x）= g（x）的圖像的交點或交點個數；參數方程更具有函數因素，屬于能隨參數的變化而變化的動態方程。它所研究的數學對象已經不是一些孤立的點，而是具有某種共性的幾何曲線[1]。認知主義學習理論強調數學學習對于知識、規律的發現與理解的過程，這就要求學生在數學學習中要通過數學知識的外在形式，進行不斷的探索、總結，進而發現數學知識中所蘊含的數學思想、知識規律。方程思想是高中數學教學中的重要解題方法，需要學生結合實際案例進行方程思想的總結與運用，已提升高中學生的數學學習能力。

一、方程思想在導數中的應用

導數考點屬于近年來高考中的重要考點內容，而方程思想在導數題型中的應用是各級、各類考試中的熱點問題。導數的單調性、極值、最值等性質的研究常常和函數與方程思想相結合，主要綜合考查學生的思維能力[2]。

例題：已知函數 f（x）=（x-a）2ex在 x=2 時取得極小值.

（1）求實數 a 的值；

（2） 是否存在區間［m，n］，使得f（x）在該區間上的值域為［e4m，e4n］？ 若存在，求出 m，n 的值；若不存在，說明理由。

在奔類題型中，利用導數研究函數的最值及其他性質時都不可避免地會經歷構建方程的過程，這道題目的突破口是建立兩種情況下的方程組：

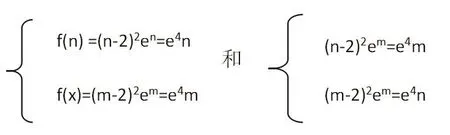
然后在運用方程思想的同時再結合函數思想進行解題，充分體現了方程思想在導數中的應用。

二、方程思想在解析幾何中的應用

在解析幾何題型中，常常會出現直線、圓、圓錐曲線之間的位置關系問題，通常會使用聯立方程組的方法進行解決。

例題：如圖 1，在平面直角坐標系 xoy 中，圓 O1，圓 O2都與直線 l∶y=kx 及 x 軸正半軸相切。若兩圓的半徑之積為2，兩圓的一個交點為 P（2，2），求直線 l的方程。

這道題考查了直線的方程、圓的方程等知識，由直線 l 的方程，可以引進參數 t，建立的直線 O1O2的方程，再根據過點 P（2，2）建立方程組，滲透了方程組的思想，在整個問題的解決過程中自始至終都滲透了建立關于參數 t 的方程的思想。

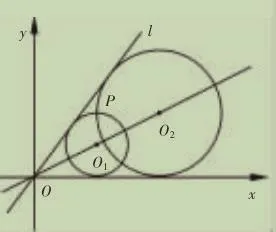
圖1

三、方程思想在不等式中的應用

不等式 2x-1＞m（x 2 -1）能夠對︱m︱ ≤2 的一切實數 m 恒成立，求得實數 x 的取值范圍。對于不等式這種問題，了解關于 x 的不等式后，這種問題會形成一種思維定式，但是應該進行視角的改變，把不等式當做關于 m 的不等式，并且構造函數 f （m）=（x2-1）m-（2x-1），這一問題就會轉化為求得 m∈［-2，2］上，使 f（m）＜0 恒成立的 x 的取值范圍。而對于一次函數來說，圖象為一條線段，如果想要 f （m）＜0，應該讓f（-2）＜0，f（2）＜0 才能解得在通常情況下，含有多個變量或參數的問題，應該對變量與參數進行積極確定，將函數關系提出來，從而使問題更加明朗。

四、方程思想在實際問題中的應用

例如一個實際應用問題：某班級組織20名學生在一條直線公路上植樹，要求以10米為間隔，并且每人植一棵樹。 在開始之前，要求將樹苗集中放在某一個樹坑旁邊，能夠讓每位同學領取樹苗所用的路程總和最小，求這個最小值。 對于這一問題來說，應該建立合適的數學模型，通過列式向函數的最值問題轉化[3]。如圖2所示。

圖2

當 i=10 或 11 時，s 的值最小，為 1000。因此往返路程的最小值為 2000 米。 對于這類問題，還有另外一種解答方式，針對軸對稱圖形的原理，兩端的樹坑旁邊放著樹苗，路程的總和相同，能夠取得一個最值。因此從兩端的樹坑移動到中間過程中，路程總和的變化是相同的，到第 10 個以及 11 個樹坑旁邊時，路程總和達到一個最值，因此只需進行兩個路程總和的計算就可以。 將樹苗放在第一個樹坑旁，路程總和為 10×（1+2+…+19）×2=10×19（1+19）×2=3800。 樹苗放在第 10 個與第 11 個旁邊時，路程總和為 10×（1+2+…+9）+10×（1+2+…+10）×2=2000。 因此，路程總和最小應為 2000 米。對于二次函數形式的構造具有重要作用，函數對實際問題的解決具有重要意義。對于這道題能夠借助實際模型的建立，通過函數解析式的方式，對函數的性質進行研究，從而促進實際問題得到合理的解決。

結語

總而言之，數學思想與數學方法是高中數學教學中的重要內容，但也是學生在數學學習中的重難點。方程是高中數學中的主線，它不僅是對中樞中相關變量之間關系的描述，更是我們解題的重要手段[4]。學生只有通過對于數學思想與方法的深入理解和熟練應用，才能真正理解數學學習的意義與價值。在高中數學學習中，對于方程思想的掌握能夠為數學學習奠定良好的基礎。方程思想在高中數學解題中而對應用，能夠起到簡化解題流程、豐富解題方法的重要作用，因此對于高中學生的方程思想的培養具有不可忽視的重要意義。

[1]陳燕青.高中數學中思想方法的應用——高中數學中的函數與方程思想[J].新課程,2015(06):95-96.

[2]牛含冰.函數思想在解題中的體現[J].高中數理化,2013(17):112.

[3] 李俠.函數與方程思想在解題中的運用舉隅[J].數理化學習 (高中版 ),2013(08):56-57.

[4]例談高中數學解題中函數與方程思想的運用[J].課程教育研究,2016(11):32-35.