執行器故障與飽和受限的航天器滑模容錯控制
于彥波,胡慶雷,董宏洋,馬廣富
(哈爾濱工業大學 航天學院, 150001 哈爾濱)
?
執行器故障與飽和受限的航天器滑模容錯控制
于彥波,胡慶雷,董宏洋,馬廣富
(哈爾濱工業大學 航天學院, 150001 哈爾濱)
針對航天器姿態控制過程中同時存在執行器故障、安裝偏差與控制受限的多約束問題,提出一種基于積分滑模面的自適應魯棒姿態容錯控制方法,所設計的控制器在滿足執行器控制能力的飽和受限約束的條件下確保系統穩定;同時,通過引入控制參數在線自適應學習策略以提高對干擾、安裝偏差以及故障變化的魯棒性,進而減小對這些信息的依賴能力,并基于Lyapunov方法分析了系統穩定性.通過數值仿真結果表明,提出的自適應積分滑模容錯控制算法能有效的保證執行器故障時航天器姿態控制系統的穩定性,并具有較強的魯棒性.
航天器;容錯控制;輸入飽和;執行器故障;安裝偏差
近年來一些先進控制理論與方法,如反饋控制[1]、自適應控制[2]、滑模控制[3-4]等及其相結合的復合控制方法在航天器實際系統控制中得到了一些應用,而滑模控制以其對不確定性的“不變性”受到學術界的廣泛關注,并在航天器姿態控制中得到了廣泛的應用[5-6].但是,對于傳統的滑模控制,當系統到達滑模面時,存在滑模的到達過程,難以保證系統的動態性能.而積分滑模由于在系統中引入了狀態的積分環節,一方面可以消除滑模面的到達過程,從而保證滑動模態下的系統與原始標稱系統的一致性;另一方面,由于積分項的存在,將對常值干擾等具有很好的抑制作用;然而積分滑模控制及其在航天控制應用相關研究鮮見報道[7-8].
容錯控制策略作為一種有效的手段來解決航天器的執行器故障問題而得到廣泛的關注,其通過設計一類特定的控制算法來保證控制系統在故障模式下的穩定性與可靠性,并在航天航空領域得到了廣泛的應用.文獻[9]為解決衛星姿態跟蹤控制問題中可能出現的執行器部分與完全失效故障,提出了一種自適應姿態容錯控制器的設計方法;文獻[10]在考慮模型不確定性、外干擾、執行器故障以及推力器力矩飽和受限的多種約束下,提出了一類魯棒自適應容錯控制器的設計方法.針對飛輪作為執行機構的故障情況下,基于動態逆和時延控制相結合的復合控制方法;文獻[11]提出了一種類似迭代學習的衛星姿態容錯控制方法.此外,考慮到對干擾以及不確定性項的抑制能力;文獻[12]基于L-2增益方法,提出了一類航天器魯棒姿態容錯控制器的設計方法,該控制器再保證了系統的最終一致有界穩定的同時滿足L-2性能指標要求.
然而,在這些容錯控制方法的研究中,并沒有考慮執行機構實際的物理約束,即沒有顯式地考慮控制力矩飽和受限的約束問題,而這種飽和受限的強非線性約束將會嚴重的影響系統的穩定性以及可靠性[13-14].此外,盡管上述文獻所提出的控制方法能夠解決航天器的外部干擾、飽和受限甚至執行器的故障容錯問題,但它們并沒有考慮實際系統存在執行機構安裝偏差的問題.在實際的航天工程中,受限于安裝工藝以及發射過程中運載器振動的影響,航天器執行機構的安裝偏差不可避免.而這種安裝偏差的存在將對姿態跟蹤性能產生影響,嚴重時將使整個姿態控制任務失敗.目前對執行器安裝偏差問題的相關研究成果相對較少[15-16],然而在這些文獻中,研究者們并沒有考慮常值干擾對系統的影響.
為此,本文在上述研究成果的基礎之上,綜合考慮外部干擾、執行機構故障、安裝偏差以及控制受限的多約束問題,提出一種新型自適應積分滑模姿態容錯控制方法;該方法在顯式地引入飽和函數以保證控制輸出受限的同時,并不依賴于執行器的在線故障診斷信息;理論上證明了所設計控制系統對執行機構故障和安裝偏差等的容錯能力與魯棒性以及系統的穩定性,并且數值仿真研究結果也驗證了所提出方法的有效性與理論的正確性.
1 航天器動力學模型與控制問題描述
為了避免奇異問題,考慮采用修正的羅德里格參數描述航天器姿態運動學與動力學方程[17]:
(1)
式中:ρ∈R3為星體坐標系相對于慣性空間坐標系的修正的羅德里格參數;ω(t)∈R3為航天器本體坐標系相對地心慣性坐標系的旋轉角速度在本體坐標系上的分量;J∈R3×3為航天器轉動慣量;Td(t)∈R3為外部干擾;u(t)∈R3為作用在星體上的合控制力矩;此外,S(·)為反對稱矩陣.
在實際的航天工程中,為保證航天器姿態控制系統的高可靠性,航天器執行機構的設計往往采用冗余配置情況,考慮圖1所示的正安裝于航天器本體坐標系的理想安裝結構.然而,在航天工程中,由于受安裝技術的限制,航天器執行機構在不同程度上存在安裝偏差.所謂安裝偏差即是反作用飛輪在實際坐標系中安裝的位置與本體坐標系中理想位置的偏差,如圖1所示.這里Δαi與Δβi(i=1,2,3,4)定義為飛輪的安裝偏差角.
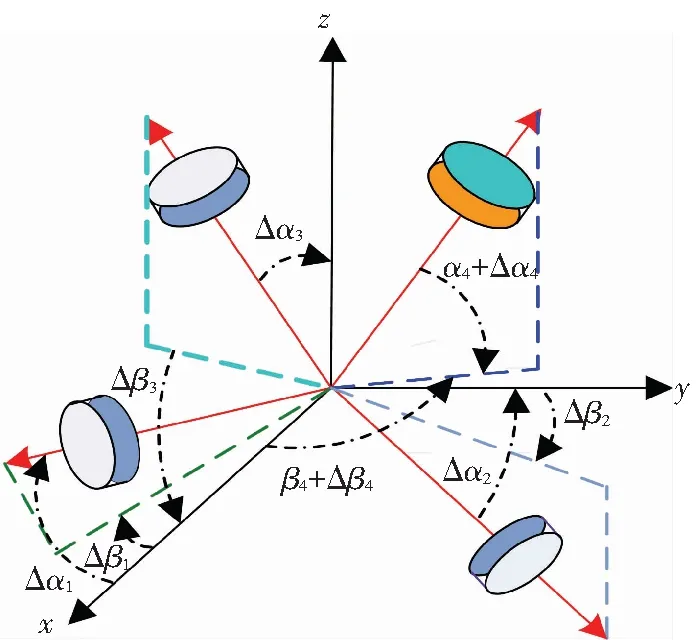
圖1 存在安裝偏差反作用飛輪配置結構
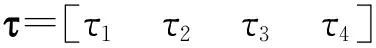
在航天器在軌運行過程中,由于執行機構要經常性地完成各種操作在軌,使得反作用飛輪時常發生故障;由此,同時考慮執行器存在故障與安裝偏差意義下的航天器的動力學方程可修改為
(2)
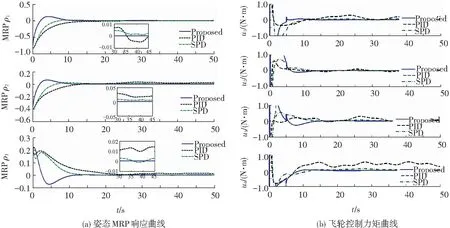
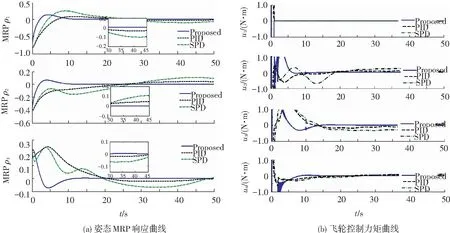
這里E定義為E=diag(e1,e2,e3,e4),式中ei為第i個反作用飛輪的有效因子,且滿足0≤ei≤1(i=1,2,3,4);當ei=1 時,表明第i個反作用飛輪工作完好;當ei=0時,表明第i個反作用飛輪完全失效;當0 為了便于控制器設計,給出如下合理假設: 假設1 對于反作用飛輪的安裝偏差角為小角度,也即安裝偏差矩陣范數有界,由此存在一個較小的常數γ使得‖ΔD‖≤γ,其中γ>0為未知常數. 假設2 對于E=diag(e1,e2,e3,e4)所描述的具有冗余反作用飛輪的故障形式,這里假設某個或某些反作用飛輪存在故障,但是失效后要求滿足約束rank(DE)=3. 假設3 假設各個飛輪的特性相同,并且其最大輸出力矩為τm,且滿足幅值受限的要求‖τ(t)‖≤τm. 基于滑模控制方法設計的控制器主要分為:1) 滑模面的選取;2) 控制律的設計,并證明系統狀態在任意初始位置有限時間到達滑模面和收斂到平衡點,從而保證了航天器狀態最終穩定的特性. 2.1 積分滑模面設計 基于航天器動力學模型式(1)的特性,選取如下積分滑模面 (3) (4) 2.2 積分滑模容錯控制器設計 由滑模面式(3)可知,對其兩端求時間導數可得 (5) 由此,可得出如下定理. 定理1 針對存在外界干擾、安裝偏差、飛輪故障以及控制受限的航天器姿態控制系統(2),滿足假設1~4,采用式(3)的積分滑模面設計如下控制律: (6) 其中 這里參數μ的選取滿足如下約束: (7) 2.3 自適應積分滑模容錯控制器設計 在積分滑模容錯控制器設計過程中,由式(7)可知,其要求系統安裝偏差矩陣、擾動以及故障的局部信息的上界應該是已知的.然而,在實際應用中,預先了解這些不確定項因素是很困難的,更不用說給出不確定性的明確范圍.為解決該問題,本文提出一種自適應積分滑模控制器的設計方法. 設計如下控制律 (8) 其中 (9) 其中κ,β>0為帶設計的自適應因子.由此給出本文的第2個主要結論. 定理2 針對存在外界干擾、安裝偏差、飛輪故障以及控制受限的航天器姿態控制系統(2),滿足假設1~4,如果采用式(3)的積分滑模面,并設計式(8)的控制律與式(9)的自適應律,那么系統的滑動模態σ(t)=0是有界穩定的,且實現上述控制目標. 式中ω0=0.1/(rad·s-1),這里假設執行機構的輸出力矩最大幅值為1 N·m.此外,反作用飛輪安裝偏差角度為Δαi=[0.2 0.1 0.2 0.3],Δβi=[0.2 0.2 0.3 0.2]. 為了驗證方法的有效性,用如下3種工況情形進行仿真驗證與比較. 1)4個反作用飛輪工作正常(無故障發生). 2)部分反作用飛輪存在故障(故障I)為e1=1;e2=0.2,t>5;e3=0.4,t>2;e4=1.即:第1個飛輪工作正常;第2個飛輪在正常工作5 s后,存在部分失效,即其控制能力將損失80%;第3個飛輪在工作正常2 s后,同時也存在部分失效,即其控制能力將損失60%;第4個飛輪工作正常. 3)部分飛輪存在故障,且某個飛輪徹底失效(故障II)為e1=0,t>1;e2=0.8,t>3;e3=0.4,t>10;e4=0.2,t>2.即:第1個飛輪在工作1 s后,其徹底失效工作,其輸出為0;第2個飛輪在工作3 s后,存在部分失效,其控制能力損失20%;第3個飛輪在工作10 s后,同時存在部分失效,其控制能力損失60%;第4個飛輪在工作2 s后,同時也存在部分失效,其控制能力損失80%. 另外,為了便于比較與分析,數值仿真過程中采用3種不同的控制方法:1)本文提出的自適應積分滑模容錯控制 (proposed);2) 文獻[13]提出的飽和比例-微分控制(SPD)方法;3) 傳統PID控制方案. 由上述仿真分析與比較,可知: 1)由圖2仿真曲線可知,所采用的3種控制器均使得該系統是穩定的,但是文獻[13]給出控制方法,使得系統存在穩態誤差,也即對帶有常值的干擾抑制能力比較差;而對于PID控制器,盡管引入積分項的作用,但是其控制器的設計并沒有顯式考慮控制受限的約束,而在仿真中采用硬飽和的方法,使得其也存在穩態誤差. 2)由圖3仿真曲線可知,所采用的3種控制器均可保證閉環系統是穩定的,但是對于PID控制,由于故障的影響,其呈現較大的震動;相當于文獻[13]給出控制方法,盡管其對反作用飛輪構故障具有一定的容錯能力,但是由于常值干擾的存在,其呈現穩態誤差;對于本文說提出的控制方法,由于其對執行機構故障具很好容錯能力,并且由于積分項與干擾抑制項的引入,其閉環控制系統的精度仍然滿足系統要求. 3)由圖4仿真曲線可知,PID控制下的系統已經失穩;對于文獻[13]提出的控制算法能夠保證系統是穩定的,但是存在震蕩,且控制精度差;而對于提出的自適應積分滑模容錯控制策略,其仍能保證系統穩定度的要求. 綜上所述,針對存在執行機構故障、控制受限、外部干擾以及執行器安裝偏差所約束下,所提出的自適應積分滑模容錯控制器在能保證航天器控制系統穩定的要求,仿真研究驗證了理論的有效性;然而,由上述的仿真結果,對于所設計的控制器,由于在控制開始階段采用較大的控制幅值去實現系統穩定,使得系統在開始階段存在姿態相應的幅值相當于其他兩種方法較大一些,在后續研究中將進一步考慮系統的暫態相應的約束,進而實現高精度的姿態控制任務. 圖2 第1種情況的仿真結果 圖3 第2種情況的仿真結果 圖4 第3種情況的仿真結果 1) 該控制器顯式的引入了飽和函數保證了執行器輸出力矩的飽和約束,有效地避免了由于執行機構飽和對系統產生的不利影響. 2) 該控制方案在不需要執行器故障信息情況下能保證容錯控制系統的漸近穩定性能,結構簡單,便于工程實現. 3) 參數自適應技術的引入有效地減小了控制系統對一些不確定性上確界的依賴,增強了系統的魯棒性能.此外,通過數值仿真對比,表明了本文魯棒容錯控制方案優越性,保證了閉環故障系統的高精度穩定. [1] XING G Q, PARVEZ S. Nonlinear attitude state tracking control for spacecraft [J]. Journal of Guidance, Control, and Dynamics, 2001, 24(3): 624-626. [2] 胡慶雷,姜博嚴,石忠.基于新型終端滑模的航天器執行器故障容錯控制[J]. 航空學報, 2014, 35(1): 249-258.[3] KRISTIANSEN R, NICKLASSON P. Satellite attitude control by quaternion-based backstepping [J]. IEEE Transactions on Control Systems Technology, 2009, 17(1): 227-232. [4] 張愛華, 胡慶雷, 霍星.過驅動航天器自適應姿態補償控制及控制分配[J]. 哈爾濱工業大學學報, 2014, 46(1):18-22. [5] HU Qinglei. Sliding mode maneuvering control and active vibration damping of three-axis stabilized flexible spacecraft with actuator dynamics [J]. Nonlinear Dynamics, 2008, 52(3): 227-248. [6] BOSKOVIC J D, LI Saiming, MEHRA R K. Robust adaptive variable structure control of spacecraft under control input saturation[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(1): 14-22. [7]CAI Wenjun, XU Jianxin. Nonlinear, integral-type sliding surface for both matched and unmatched uncertain systems[J]. IEEE Transactions on Automatic Control, 2004, 49(8): 1355-1360. [8]HU Qinglei, ZHANG Youmin, HUO Xing, et al. Adaptive integral-type sliding mode control for spacecraft attitude maneuvering under actuator stuck failures [J]. Chinese Journal of Aeronautics, 2011, 24(1):32-45. [9]JIANG Ye, HU Qinglei, MA Guangfu. Adaptive backstepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures [J]. ISA Transactions, 2010, 49(1):57-69. [10]CAI Wenchuan, LIAO Xiaohong, SONG D Y. Indirect robust adaptive fault-tolerant control for attitude tracking of spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1456-1463. [11]JIN J, KO S, RYOO C K. Fault tolerant control for satellites with four reaction wheels [J]. Control Engineering Practice, 2008, 16(10): 1250-1258. [12]HU Qinglei. Robust adaptive sliding-mode fault-tolerant control with L2-gain performance for flexible spacecraft using redundant reaction wheels [J]. IET Control Theory & Applications, 2010, 4(6): 1055-1070. [13]WALLSGROVE R J, AKELLA M R. Globally stabilizing saturated attitude control in the presence of bounded unknown disturbances [J]. Journal of Guidance, Control, and Dynamics, 2005, 28(5):957-963. [14]LIM H C, BANG H. Adaptive control for satellite formation flying under thrust misalignment[J]. Acta Astronautica, 2009, 65(1/2): 112-122. [15]HU Qinglei, LI Bo, ZHANG Aihua. Robust finite-time control allocation in spacecraft attitude stabilization under actuator misalignment [J]. Nonlinear Dynamics, 2013, 73(1):53-71.[16]姜野, 胡慶雷, 馬廣富. 航天器時延自適應變結構容錯控制[J]. 控制與決策. 2010, 25(5):651-656. [17]SIDI M J. Spacecraft dynamics and control [M]. Londom: Cambridge Univorsity Press, 1997. [18]HU Qinglei, LI Bo, ZHANG Youmin. Nonlinear proportional-derivative control incorporating closed-loop control allocation for spacecraft [J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3):799-812. [19]IOANNOU P, SUN Jing. Robust adaptive control [M]. Englewood Cliffs, NJ: Prentice-Hall, 1996. (編輯 張 紅) Sliding mode fault tolerant control for spacecraft under actuator fault and saturation YU Yanbo, HU Qinglei, DONG Hongyang, MA Guangfu (School of Astronautics, Harbin Institute of Technology, 150001 Harbin, China) A fault tolerant control scheme based on integral sliding mode surface is developed for spacecraft attitude stabilization in the presence of actuator faults, misalignments, magnitude saturation and external disturbances simultaneously. This approach is based on a novel integral-type sliding mode control strategy to compensate for these un-desired issues without controller reconfiguration. Especially, it guarantees the reachability of the system states by involving adaptive control technique to relax the boundary information in advance. A sufficient condition for the controller to accommodate magnitude saturation is also presented and then the fault tolerant attitude control system can be guaranteed theoretically to be asymptotically stable by using Lyapunov method. Numerical simulation results shows that the proposed control law can quarantee the stability of the spacecraft attitude control system in the presence of actuators′ failures, and it has good robust performance. spacecraft; fault tolerant control; input saturation; actuator fault; misalignment 10.11918/j.issn.0367-6234.2016.04.003 2014-11-25. 國家自然科學基金 (61174200, 61273175); 教育部新世紀優秀人才計劃(NCET-11-0801); 黑龍江省青年基金(QC2012C024); 高等學校博士學科點專項科研基金(20132302110028). 于彥波(1985—),男,博士研究生; 胡慶雷(1979—),男,教授,博士生導師; 胡慶雷, huqingleihit@gmail.com. V448.22 A 0367-6234(2016)04-0020-06 馬廣富(1963—),男,教授,博士生導師.
2 自適應積分滑模姿態容錯控制器設計
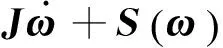
3 仿真驗證與比較
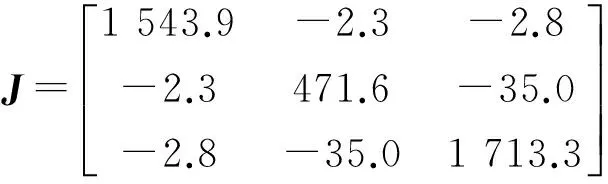

4 結 論

