結構抗力指標對飛艇囊體變形的影響

沈克利，付功義，王鳳欣，陳永霖

(上海交通大學 空間結構研究中心，200240 上海)

?

結構抗力指標對飛艇囊體變形的影響

沈克利，付功義，王鳳欣，陳永霖

(上海交通大學 空間結構研究中心，200240 上海)

為研究主要結構抗力指標變化下飛艇囊體變形的狀態與特征，用數值方法對一類典型飛艇的充氣囊體在不同抗力指標下的變形進行了數值分析.分析結果表明：彈性模量對變形的影響是非線性的，泊松比對變形的影響是線性的，彈性模量對變形的影響明顯強于泊松比；相同工況下，囊體長度與絕對變形量之間為平方關系，與相對變形量之間為線性關系；長細比在4～5時，相對變相量曲線近似為水平直線.因此，選用彈性模量較大的膜材、設計合理的飛艇長度并使長細比控制在4～5范圍內，有利于減小飛艇囊體的相對變形.

飛艇囊體；變形；數值分析；結構抗力指標；囊體材料特性；飛艇結構幾何特性

自從1852年法國工程師亨利·吉法爾[1]成功制造世界上首架動力驅動的可駕駛飛艇后，飛艇很快就迎來了它的黃金歲月.各國重視飛艇在軍事中的應用，在第一次世界大戰前后，德國就建立了用于海上巡邏、遠程轟炸、空中運輸等軍事活動的飛艇部隊[2-3].但是1937年的“興登堡”號空難[4]阻礙了飛艇進一步的應用與發展.隨著材料科學等相關學科的發展，提高飛艇的各項性能指標成為了可能，尤其在無線通信系統和高分辨率對地觀測系統等應用中的廣闊前景，再次激發了人們的興趣，飛艇平臺獲得了它的“第二次生命”[5].

飛艇艇體有柔性結構、半剛性結構以及剛性結構3種結構形式[6-8]，不同的結構形式對應于不同的應用目的與飛行環境.其中，柔性結構的艇體由單純的充氣囊體構成；而半剛性結構以及剛性結構的艇體則由充氣囊體與剛性結構體系組成剛柔混合結構體系，其力學協調關系更為復雜.

無論飛艇艇體為何種結構形式，把握充氣囊體的力學行為特征是飛艇結構體系設計的一個重要基礎.尤其是對于體量較大的飛艇結構，其結構行為的變化還將表現在對氣動特性[9-10]以及浮重平衡的影響.對于近十多年來國內外所關注的平流層飛艇，利用剛性結構體系的“籠子”效應，可以有效解決平流層飛艇下降過程中的囊體進氣難的問題，避免出現明顯的超冷超熱效應，但是“籠子”行為的構成也依賴于充氣囊體在不同壓差條件下對其力學特征的準確把握.本文利用經典力學理論及商用有限元軟件ABAQUS，對典型飛艇外形囊體進行數值計算，對計算結果進行比較分析，探討結構抗力指標(材料彈性模量、泊松比、囊體長度以及囊體長細比)對飛艇充氣囊體變形的影響，以便為平流層飛艇的設計提供參考.

1 影響因素的分類

通常可以根據荷載效應(S)和結構抗力(R)兩個指標對變形的影響因素進行分類，見表1.

表1 兩種指標下的影響因素

2 充氣囊體的力學分析模型與方法

2.1 充氣囊體的幾何外形與參數

本文使用的飛艇平臺囊體的長細比為2.65，外形曲線為非標準三葉玫瑰線的一枝.在平面X-Y內投影曲線為

式中a為飛艇長度，本模型中a=160 m.

飛艇囊體母線如圖1所示.

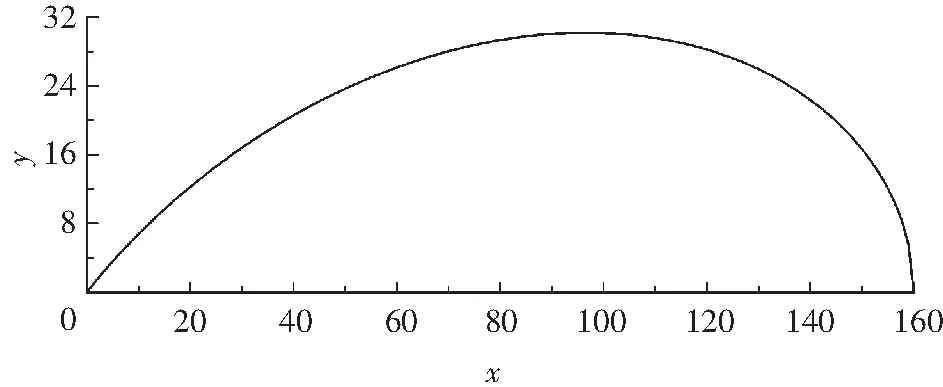
圖1 飛艇囊體母線

用Matlab計算的飛艇囊體的幾何特性參數見表2.

表2 囊體幾何參數

2.2 靜力計算中無約束懸浮飛艇的處理方法

對懸浮于空氣中的飛艇進行有限元靜力分析計算時，不能把飛艇處理為全自由度結構.由于有限元靜力分析的計算模型中應無機構和剛體運動[11-12]，而全自由度結構剛度矩陣奇異，數值計算無法進行.因此在數值分析中，通常可以采用以下兩種方法計算懸浮飛艇的靜力問題.

1)在ANSYS中可以利用慣性釋放(inertia relief)技術對完全無約束的飛艇平臺進行靜力分析.慣性釋放指用結構的慣性力來平衡外力.盡管結構沒有約束，分析時仍假設其處于一種“靜態”的平衡狀態.

利用慣性釋放技術進行數值計算的過程如下[13].

a)計算結構所受合力以及相對于結構中心的外力矩，設為FT(t)、Fr(t).

b)根據平衡條件，在結構上施加平動加速度及轉動加速度為

式中：FT(t)、Fr(t)分別為t時刻結構所受的平動力和轉動力;aT(t)、ar(t)分別為t時刻結構相對于重心的平動加速度和轉動加速度.

c)根據新的外力，重新計算結構受力.

2)用ABAQUS進行靜力計算時，可以通過施加一定的約束條件使有限元分析能進行下去.一種常用的做法是，用縱截面(X-Y)面剖切囊體，在截面處施加Z向約束，飛艇頭部施加全約束，尾部只允許X方向的位移.考慮吊掛荷載時，也可以在吊掛處施加全約束.

慣性釋放的方法忽略了重力荷載效應的影響，會產生較大誤差.因此本文在使用ABAQUS作數值計算時，使用第2種方法處理約束.

3 算例驗證

飛艇充氣囊體是典型的大曲率充氣膜結構，囊體頭錐、尾錐曲率較大，對于該類充氣膜結構，很難通過解析的方法求解出其環向應力的精確值.

文獻[14-15]推導了飛艇充氣囊體環向應力近似計算公式為

(1)

式中：σHT為環向應力理論值;R(x)為截面半徑;Δp為壓差;t為膜材厚度.

分別用式(1)和有限元軟件ABAQUS，計算上述三葉玫瑰線形囊體在零度攻角下200、300、400、500、600 Pa純壓差下囊體環向應力最大值.材料厚度0.000 264 m，材料彈性模量8 GPa.計算結果見表3.

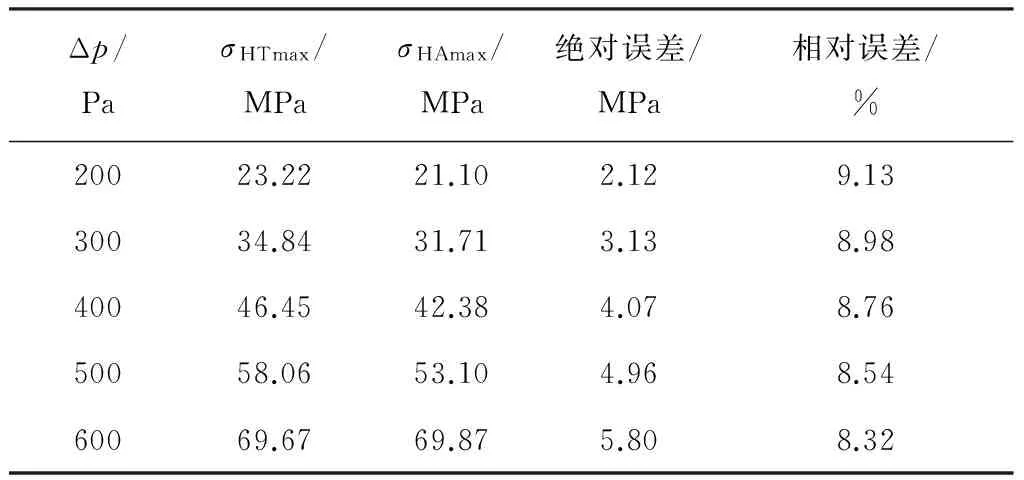
表3 環向應力理論值與數值計算值的對比(三葉玫瑰線形)

注：σHT代表環向應力理論值，σHA代表環向應力數值計算值.

式(1)是圓管形充氣膜結構的環向應力解析值.為消除由于環向應力近似對計算帶來的影響，分別用式(1)和ABAQUS計算長160 m、長細比2.67的充氣圓管(圖2)，計算結果見表4.計算表明，在200～600 Pa內，相對誤差不超過1.7%.理論與數值結果吻合的較好.

圖2 充氣圓管

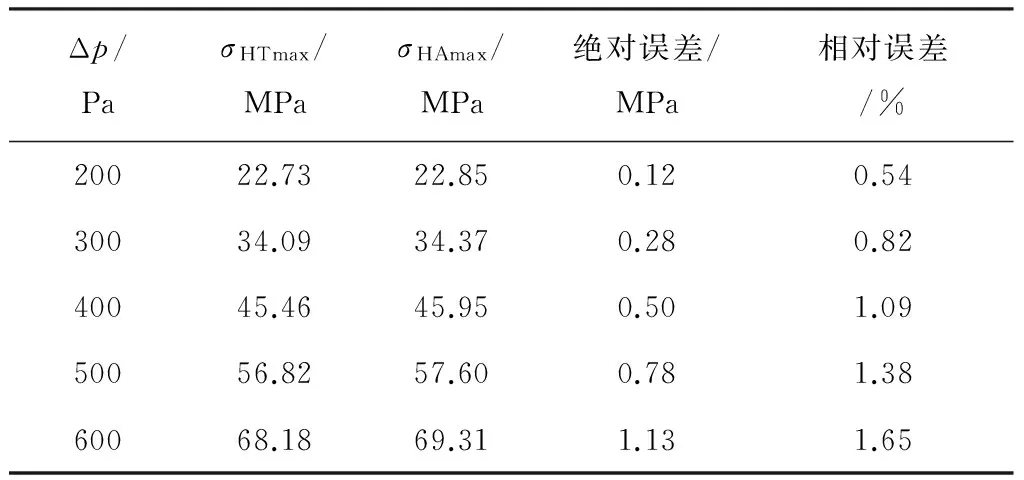
Δp/PaσHTmax/MPaσHAmax/MPa絕對誤差/MPa相對誤差/%20022.7322.850.120.5430034.0934.370.280.8240045.4645.950.501.0950056.8257.600.781.3860068.1869.311.131.65

綜上分析，對于大曲率充氣膜結構，若想僅通過理論推導來獲取解析解并不現實，即使通過簡化獲取了解析解，由于簡化而引起的誤差也將較大.數值工具是計算大曲率充氣膜結構的有效工具，其相對誤差不到1.7%，數值解和理論解吻合的較好.

4 主要抗力指標對變形的影響

4.1 材料彈性模量和泊松比對囊體變形的影響

彈性模量和泊松比是膜材最重要的兩個力學性能指標，也是兩個重要的結構抗力指標.如何選擇合適的材料彈性模量和泊松比是飛艇結構設計的重要內容.

目前已知可用于平流層飛艇囊體膜材的彈性模量最大值在8～9 GPa，選擇6.0、6.5、7.0、7.5、8.0 GPa這5個彈性模量值，計算各彈性模量下的囊體最大變形量以探究彈性模量對長度方向變形的影響，計算結果見表5.膜材的泊松比一般為0.2～0.5，選擇0.25、0.30、0.35、0.40、0.45這5個泊松比值，計算各泊松比下囊體最大變形量，計算結果見表6.

表5 各彈性模量下囊體最大變形量(L=160 m,p=400 Pa,ν=0.3)

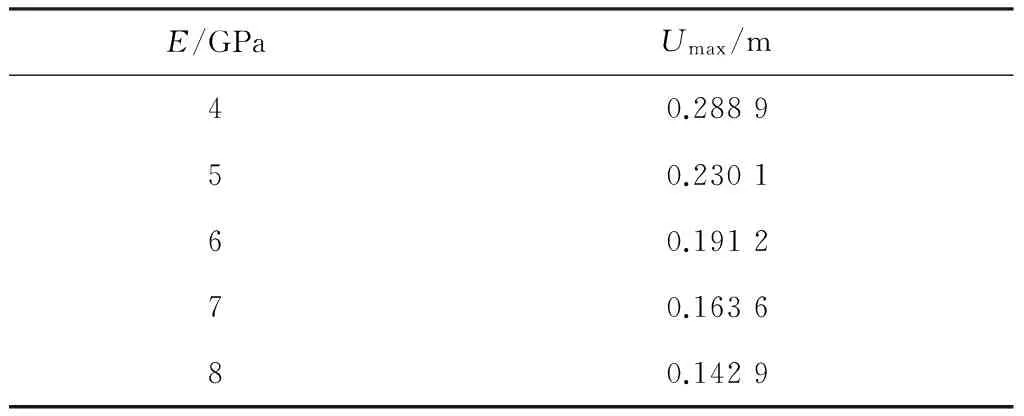
E/GPaUmax/m40.288950.230160.191270.163680.1429

表6 各泊松比下囊體最大變形量(L=160 m,p=400 Pa,E=8 GPa)

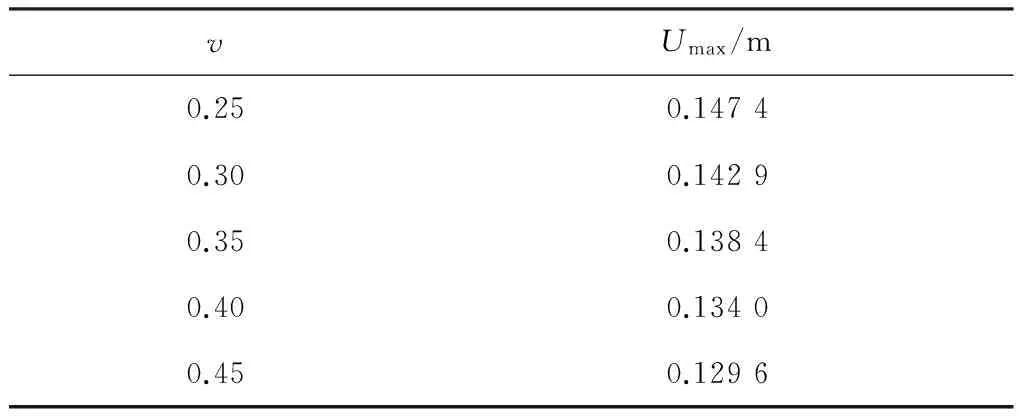
vUmax/m0.250.14740.300.14290.350.13840.400.13400.450.1296

計算結果表明：彈性模量與最大變形量曲線呈反比例，如圖3所示.當彈性模量由4 GPa開始，每增加一個1 GPa，增加到8 GPa時，變形分別減小0.058 8、0.038 9、0.027 6、0.020 7 m.隨著彈性模量的增大，曲線斜率的絕對值不斷減小，彈性模量對變形的影響減弱.泊松比與變形關系曲線呈直線，變形隨泊松比的增大而減小，泊松比每增大0.05，變形減小約0.004 5 m.從圖3可見，彈性模量對變形的影響比泊松比的影響更加明顯.

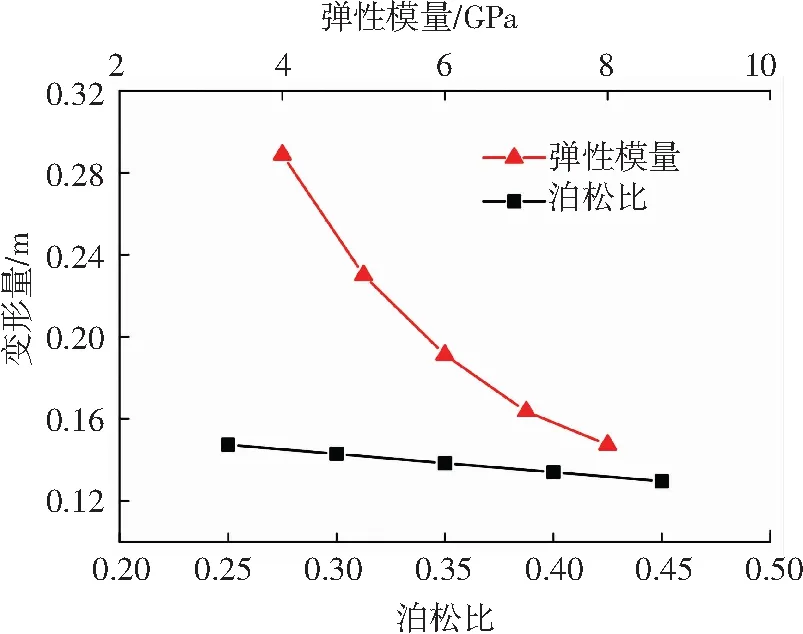
圖3 不同泊松比和彈性模量下的囊體變形量

在彈性模量、泊松比兩個抗力指標中，彈性模量對變形的影響是非線性的，泊松比對變形的影響是線性的，彈性模量對變形的影響強于泊松比對變形的影響.因此，在飛艇膜材選擇時，應選擇彈性模量和泊松比均較大的膜材，但當彈性模量、泊松比同時達到較大時，首選彈性模量較大的膜材.

4.2 囊體長度對囊體變形的影響

相同材料彈性模量和長細比的情況下，對比120、160、200、240 m這4種囊體尺度在同一工況下的最大變形，數值計算結果見表7.

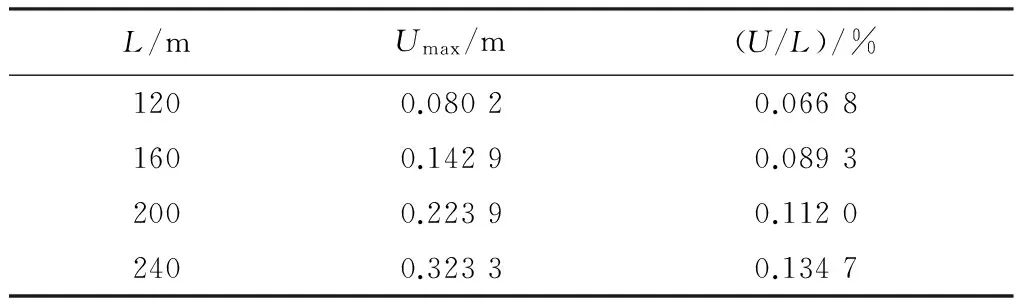
表7 各長度下囊體最大變形量(E=8 GPa,p=400 Pa)

對比數值計算變形量分布云圖，發現變形變化趨勢相似，但數量值卻相差很大，變形量并不與艇體長度成正比關系.如，240 m艇體最大絕對變形量比120 m艇體最大絕對變形量大4倍左右.各長度下的變形量有以下關系：

(2)

(3)

式中：i,j=1,2,3,4.

對數值結果的分析整理，得出如下結論：囊體長度變為原來的n倍時，絕對變形量變為原來的n2倍，相對變形量U/L是原來的n倍，如圖4所示.

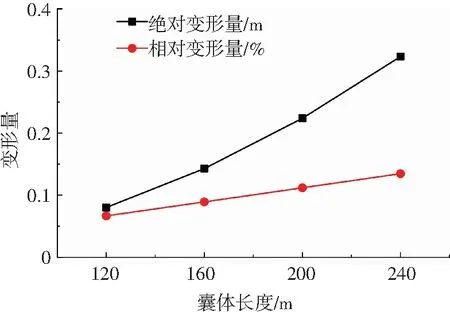
圖4 囊體長度—囊體最大變形量曲線

4.3 囊體長細比對囊體變形的影響

為考察長細比對變形的影響，對比一組不同長細比下的充氣囊體在相同工況下的囊體變形.選擇囊體長度為160 m，材料彈性模量、密度均相等，計算在長細比為2.00、2.65、3.00、4.00、4.50、5.00這6種情況下的囊體絕對變形量和相對變化量.長細比為2、3、4、5的囊體外形如圖5所示，各長細比囊體變形計算結果見圖6及表8.

在圖6中，長細比—絕對變形量曲線隨長細比增大而減小，但長細比—相對變形量曲線在長細比為3～4的區段出現了極值點.這是因為囊體變形包含了由外荷載引起的彈性變形和與結構外形有關的結構變形，屬于非彈性變形.對于如圖5所示的不同長細比的充氣膜結構，長細比越大，非彈性變形越小.因此，即使各長細比的囊體在不同的外荷載作用下發生等量的彈性變形，但總的變形量也不會相等，長細比大的總變形小，兩種變形量共同決定總變形量.該極值點的出現反映了彈性變形和結構變形各自隨壓差變化曲線是非線性的.

圖5 不同長細比下的囊體外形

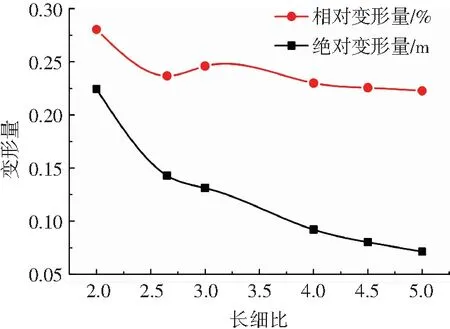
圖6 長細比—囊體最大變形量曲線

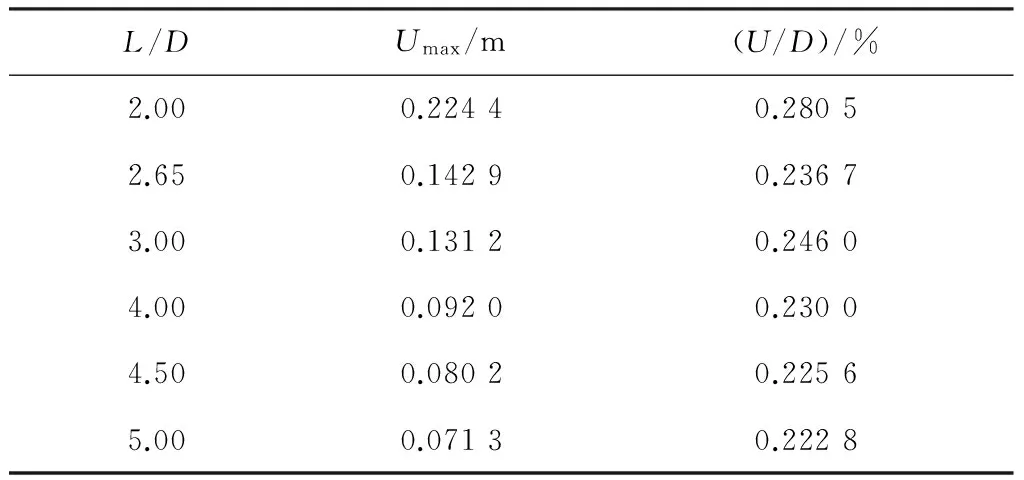
L/DUmax/m(U/D)/%2.000.22440.28052.650.14290.23673.000.13120.24604.000.09200.23004.500.08020.22565.000.07130.2228

由圖6可知，長細比2～3區段，絕對變形量、相對變形量曲線斜率均較大，該區段長細比對變形影響十分明顯；長細比3～4區段絕對變形量、相對變形量曲線斜率較前2～3區段明顯偏小，但又較4～5區段明顯偏大；長細比4～5區段，絕對變形量曲線接近直線，相對變相量曲線平緩，近似水平線.

另外，值得注意的是：飛艇是依靠浮升氣體提供浮升力的，而浮升力與飛艇體積正相關.在飛艇結構設計時，給定飛艇有效荷載，則飛艇囊體的體積V也可以近似估算出來，在V為定值的情況下，長細比L/D大意味著L較長.較大的長度無論是對于飛艇空氣靜力學、動力學、飛行控制，還是對于飛艇的制造，都是不利的.美國《Airship Design Criteria》(NO.FAA-P-8110-2)所用的有關飛艇力學計算的長細比不大于6也是基于這個考慮的.

因此，在飛艇結構設計時，長細比應位于相對變形量曲線為近似水平直線的4～5區段，盡可能使長細比接近4以避免囊體長度過長.

5 結 論

1)材料剛度與最大變形量關系曲線呈反比例，泊松比與最大變形量曲線為正比例，彈性模量對變形的影響強于泊松比.

2)同種工況條件下，囊體長度變為原來的n倍時，絕對變形量變為原來的n2倍，相對變形量變為原來的n倍.

3)長細比4～5區段時相對變形量曲線近似水平直線，選擇長細比為4～5并盡可能接近4對減小相對變形是有利的.

[1] 甘曉華，郭潁.飛艇技術概論[M].北京，國防工業出版社，2005.

[2] RYAN, D E. The airship′s potential for intertheater and intratheater airlift[R]. Alabama: Air University School of Advanced Airpower Studies United States Air Force Maxwell Air Force Base, 1992.

[3] GERKRN L C. Airships: history and technology[M]. Chula Vista, California: American Scientific Corporation, 1990:464.

[4] ARCHBOLD R. Hindenburg: an illustrated history[M]. Toronto: Viking Studio/Madison Press, 1994.

[5] WILSON J R. A New era for airship[J]. Aerospace America, 2004, 42(5):27-31.

[6] KHOURY G A, GILLET J D. Airship technology[M]. Cambridge, UK: Cambridge University Press, 1999.

[7] LIAO L, PASTERNAK I. A review of airship structure research and development[J]. Progress in Aerospace Science, 2009, 45(4/5)83-96.

[8] 楊艷初，王生，姜魯華.飛艇總體構形新概念設計[C]// 2007年中國浮空器大會論文匯編. 北京: 中國浮空器大會論文集，2007: 39-43.

[9] LIU Jianmin, LU Chuanjing,XUE Leiping,et al. Coupling computation of the flow field and the large deformation of membrane structure of stratosphere airships[J]. Journal of Hydrodynamics, 2008, 20(4): 536

[10]LI Yuwen, NAHON M, SHARF I. Airship dynamics modeling: a literature review[J].Progress in Aerospace Sciences, 2011,47(3):217-239.

[11]LIN Liao. A Study of Inertia Relief Analysis[C]//Proceedings of the 52ndAIAA/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Denver, Colorado:AIAA, 2011:1-10.

[12]張少雄，楊永謙.慣性釋放在油船結構強度直接計算中的應用[J].船海工程，2004，(4): 4-6.

[13]劉平. 大體積柔性充氣結構流固耦合性能分析方法研究[D]. 上海: 上海交通大學, 2014.

[14]楊留義. 囊體結構設計及其氣彈特性計算分析[D].哈爾濱：哈爾濱工業大學, 2012.

[15]黃迪，趙海濤，邱野，等. 平流層飛艇蒙皮強度建模與仿真研究[J].計算器仿真，2013，30(1)：150-153.

(編輯 張 紅)

Influence of structural resistance indexes on deformation of airship envelope

SHEN Keli，FU Gongyi，WANG Fengxin，CHEN Yonglin

(Space Structures Research Centre，Shanghai Jiaotong University，200240 Shanghai，China)

To explore deformation characteristics of airship envelope with different structure resistance indexes, a numerical method was employed to analyze the deformation of a kind of typical airship envelope with different structure resistance indexes. Analytical results show: the effect of elastic modulus on deformation is nonlinear, the effect of poisson ratio on deformation is linear, and the effect of elastic modulus on deformation is obviously stronger than that of poisson ratio. Meanwhile, a square relationship between envelope length and its absolute deformation, a linear relationship between envelope length and relative deformation have been certified under the same working condition. What is more, it was testified that the curve between slenderness ratio and relative deformation was horizontal when slenderness ratio was between 4 and 5. Therefore, to reduce the relative deformation, it is beneficial to adopt envelop materials with large elastic modulus anddesign airship with appropriate length to make the slenderness radio between 4 and 5.

airship envelope；deformation；numerical analysis；structure resistance indexes; properties of envelope material; the airship structure geometrical features

10.11918/j.issn.0367-6234.2016.04.017

2014-10-31.

沈克利(1989—)，男，碩士研究生；

付功義(1957—)，男，教授，博士生導師.

付功義，gyfu@sjtu.edu.cn.

V274

A

0367-6234(2016)04-104-05