水下爆炸船體結構響應間斷伽遼金法數值模擬
于福臨,郭 君,姚熊亮,任少飛
(哈爾濱工程大學 船舶工程學院, 150001 哈爾濱)
?
水下爆炸船體結構響應間斷伽遼金法數值模擬
于福臨,郭 君,姚熊亮,任少飛
(哈爾濱工程大學 船舶工程學院, 150001 哈爾濱)
為求解水下爆炸強間斷流場,采用Level Set方法定位多相流界面位置,應用虛擬流體方法處理鄰近界面兩側物理量,并用RKDG方法進行空間和時間的離散,求解流場的Euler方程,并進行一維、二維評價,計算結果能夠較好地反映水下爆炸沖擊波產生、傳播、反射和爆炸產物的膨脹等現象.最后,結合大型非線性有限元軟件ABAQUS,模擬了船體板在水下爆炸載荷作用下的變形和響應特征.模擬結果表明,間斷迦遼金法能夠實現對水下爆炸船體結構響應精確模擬,板架結構響應與爆心距離成反比.
水下爆炸;間斷伽遼金;載荷計算;結構響應;有限元;數值模擬
水面艦船在作戰中,會受到水雷、魚雷等水下武器的攻擊,對艦船生命力構成威脅.國內外學者對水下爆炸載荷及結構響應方面開展了廣泛的研究.試驗研究是最有效的手段,國內外開展了一些實船[1]、艙段以及模型試驗[2],但水下爆炸試驗耗資巨大.解析法只能對簡單邊界的水下爆炸載荷進行求解,文獻[3-4]給出了水下爆炸載荷的經驗公式,但是經驗公式無法對過程進行描述,而且難以對結構響應進行求解.隨著計算機性能的提高,數值技術成為研究水下爆炸的一種有效手段,發展出了有限元、有限體積、邊界元和無網格等數值方法.間斷伽遼金方法是介于有限元法和有限體積法之間的一種算法[5],具備兩者的優點.一方面,本質上是一種高精度的微分方程空間離散方法,在離散過程中使用弱形式積分,具有有限維解,在單元內使用多項式逼近物理量的真實值,通過簡單的增加多項式次數,即可直接提高單元階數,構造高階格式,與有限元方法相似;另一方面,間斷伽遼金方法引入數值通量的概念,在單元與單元間計入流場間斷,使其可用于沖擊波等強間斷現象的捕捉,同時還具備多種非線性的限制器,在保證其精度的前提下,抑制非物理振蕩,這與有限體積法相似.間斷伽遼金法本身就具有高分辨率捕捉的特性,能有效處理水下爆炸中出現的壓力、密度、速度等物理量的間斷.
本文基于間斷伽遼金方法,結合虛擬流體方法(ghost fluid method)和Level Set方法,編制計算程序,對一維和二維算例進行了計算,并模擬了近壁面條件下的水下爆炸流場特性,最后結合ABAQUS,對水下爆炸載荷作用下船體結構的變形和響應特征進行了模擬.
1 數值模擬方法
1.1 控制方程
對于無黏可壓縮流場,歐拉方程組可表示[6]為
(1)
對于二維計算區域,式(1)可表示為
(2)
式中:ρ為流體密度;p為壓力; u為沿x軸速度;v為沿y軸速度;E為單位體積總能量.
1.2 狀態方程
氣體采用理想氣體狀態方程描述[7]
(3)
對于水而言,采用Tait狀態方程描述[8]為
(4)
式中:ρ為密度;B取3.31×108Pa;γ=7.15;A=105Pa;ρ0=1 000 kg/m3.
1.3 空間與時間離散
對于水下爆炸無黏可壓縮性流場,在空間上采用間斷伽遼金法進行離散,設流體計算區域記為Ω,在式(1)兩側同時乘以試探函數w(x),引入流通量得[9]
(5)
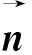
(6)
式中,Pm(x)、Pn(y)分別為Legendre多項式,將式(6)帶入式(5)即得到離散方程.
采用3階TVDRunge-Kutta方法對流體力學方程組進行時間離散[11],具體形式為
(7)
式中U(0)為tn時刻流場物理特性.
1.4 界面追蹤
應用Level Set方法定位多相流界面位置,Level Set方程如下[12]
(8)
式中:V=(u,v,w)為運動速度;Φ為距離函數.
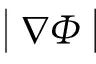
(9)
式中:Φ0為初始時刻Φ值;S(Φ0)為光滑函數.
1.5 虛擬流動方法
原始的虛擬流動方法簡單的采用虛擬流體物理場的特性對應真實流體的物理場特性,方法較為簡單,在處理強間斷問題時,無法給出精確的界面狀態[13],誤差較大,甚至無法計算.
本文使用修正的真實虛擬流動方法重構界面狀態,使用兩相流黎曼問題的求解方式,沿掃掠方向拾取狀態參數.為了方便描述,沿x向描述這種算法.界面位于xL和xR之間,線段l1和l2代表界面.
界面法向n使用以下近似[14]:
(10)

設xL和xR處的狀態參數為
(11)
速度分解成法向和切向分量為
使用投影態給出的參量求解黎曼問題為
(12)
最后,通過重新結合黎曼解得到的中間狀態和切向速度得到了界面狀態參數為
(13)
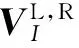
2 算例驗證
2.1 一維算例
采用RKDG方法編制計算程序,模擬自由場空中爆炸流場,并與Henrych經驗公式進行對比.表1和圖1,2分別為不同爆距條件下沖擊波超壓峰值計算值與經驗值對比結果.
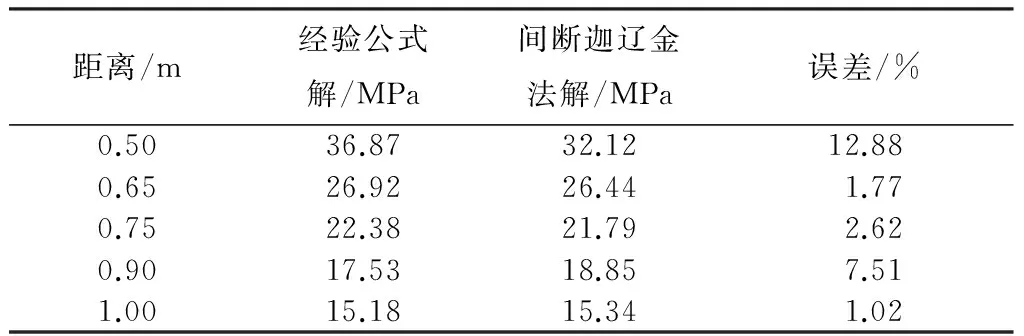
表1 沖擊波超壓峰值計算結果
從表1可以看出,RKDG方法計算得到的沖擊波超壓峰值與經驗公式吻合很好,最小誤差僅為1.02%,最大誤差不超過13%,說明本文提出的RKDG計算程序能夠有效模擬空中爆炸沖擊波載荷特性.
2.2 二維激波管算例
選取文獻[15]中的算例,計算區域區取為[0,325]×[-44.5,44.5],一Mach數為1.22的激波通過一個氣泡,氣泡中心位于(175,0),半徑25,激波位于x=225,向左傳播,網格為320×80.無量綱化初始條件:氣泡內ρ=0.138,u=0,v=0,p=1;激波前ρ=1,u=0,v=0,p=1;激波后ρ=1.376 4,u=-0.394,v=0,p=1.569 8.
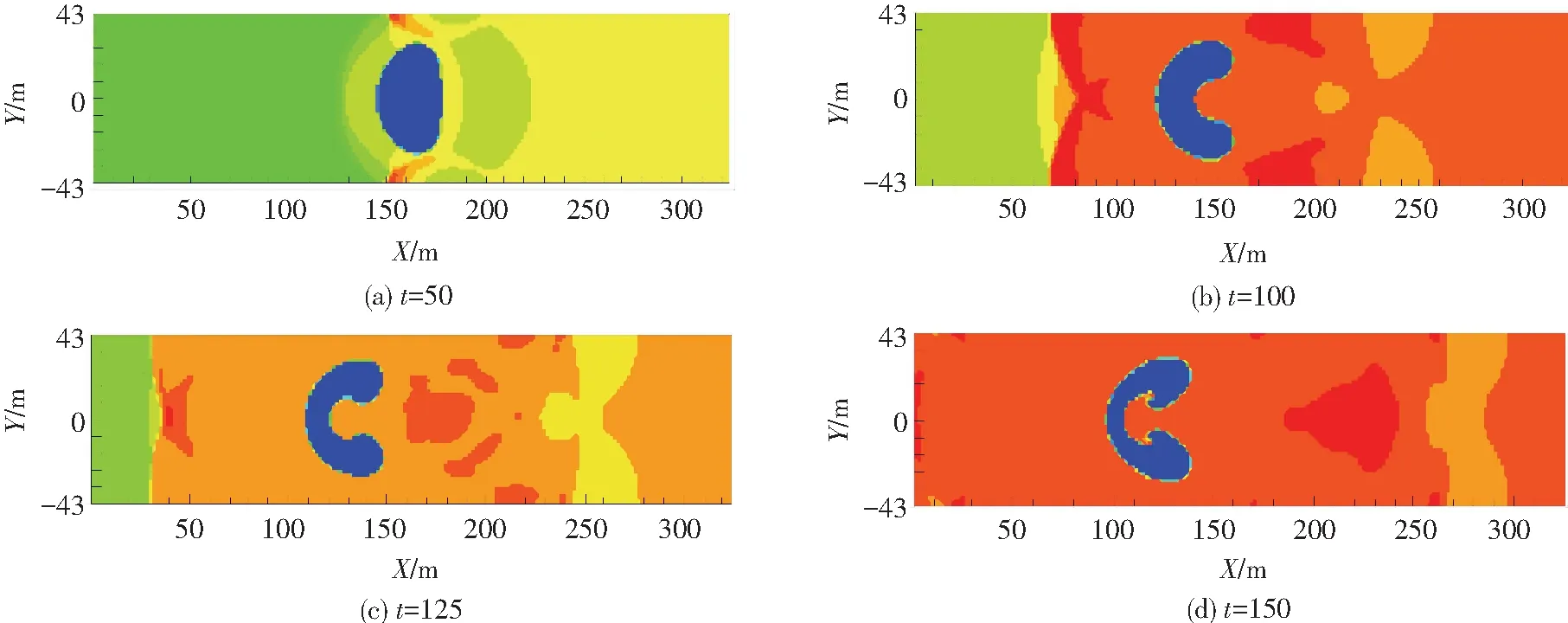
圖1 流場不同時刻密度
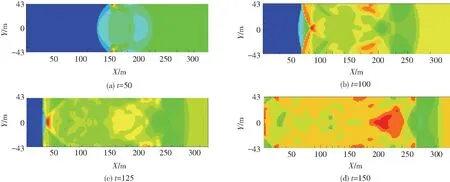
圖2 流場不同時刻壓力
由圖1可以看出,平面沖擊波與氣泡相互作用后,氣泡向左運動,當沖擊波掃過氣泡后,氣泡的迎波面(右側)向內凹陷,而背波面(左側)形態基本保持不變.隨著時間推移,迎波面繼續向內凹陷,迎波面形成渦環狀結構,這是由于沖擊波誘導氣泡發生射流而形成的漩渦.由圖2可以看出,沖擊波傳播至氣泡處時,氣泡內部壓力升高,并在氣泡上下靠近壁面處形成局部高壓,在t=100時,沖擊波在傳播方向的最前方形成高壓區,隨著時間推移,沖擊波誘導氣泡發生射流并在射流后方形成高壓區.
由一維和二維算例可以看出本文的數值方法計算沖擊波壓力值較精確,能夠實現對流場間斷的高分辨率捕捉,對激波具有較高的分辨率,通過在間斷附近構造Riemann問題的方式,能有效的抑制界面附近非物理震蕩,并能消除間斷附近的數值耗散.
3 近壁面水下爆炸沖擊波載荷數值模擬
初始時刻,爆炸流場內密度為1 630 kg/m3,壓力為7.8×109Pa,外部流場水的密度為1 000 kg/m3,壓力為1×105Pa,爆炸初始流場半徑為1 m,上邊界為固壁邊界條件.
初始時刻,沖擊波和材料界面都迅速向外膨脹,并向周圍流場中釋放一道球面沖擊波,稱為主波,同時形成一道朝向氣泡中心匯聚的內聚沖擊波,如圖3(a).當沖擊波傳播至壁面后,被剛性壁面完全反射,并仍以沖擊波的形式朝向氣泡傳播.當沖擊波傳播至氣泡表面后,由于氣泡外部介質的阻抗高于氣泡內部,因此一部分沖擊波將以稀疏波的形式反射回流場中,而另一部分將以沖擊波的形式透射入氣泡內部,如圖3(b)、3(c).由于主波相對壁面來說是以大角度入射的斜沖擊波,因此開始出現馬赫反射現象.主波脫離壁面表面,形成馬赫桿結構,與壁面反射波一起交匯于“三點波”處,并在三波結構后出現一道滑移線.主波、壁面反射波以及馬赫桿均為沖擊波,波前波后的密度、壓力和Ma均間斷,而滑移線內側的壓力連續,密度和Ma間斷,如圖3(d)、(e).當稀疏波傳播至壁面,即從低阻抗介質入射至高阻抗介質,又將以稀疏波的形式被反射,傳播方向相反的兩道稀疏波相互疊加,最終使得該區域內的壓力低于臨界壓力以下,并形成空化,如圖3(f)所示.
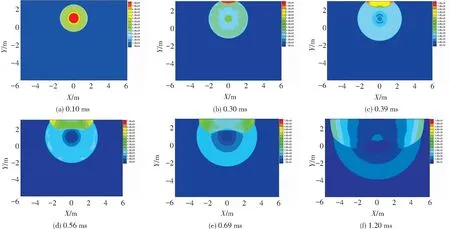
圖3 近壁面水下爆炸流場物理特性
4 船體板架結構響應數值模擬
4.1 結構模型及工況設置
建立船體板架結構有限元模型,模型尺寸為6 m×4 m,厚度20 mm,綜合考慮計算精度和計算耗時,選取網格數量120×80,編制水下爆炸載荷計算程序并結合非線性有限元軟件ABAQUS,對船體板架結構響應進行數值模擬.上邊界為船體板結構,板四周剛性固定.應用RKDG方法計算整個流場載荷,并與ABAQUS軟件結合,計算船體板架響應特性.設板架中心的坐標為O(0 m,0 m),選取4個考核點,坐標依次為A(2.0 m,0 m)、B(1.5 m,0 m)、C(1.0 m,0 m)、D(0.5 m,0 m).
4.2 船體板架結構毀傷變形分析
當沖擊波傳播作用到板架結構時,板架承受壓力從0.1 MPa增大GPa至級,達到材料屈服極限,結構出現塑性變形,計算得到的船體板架結構變形如圖4所示.從圖4可以看出,沖擊波作用范圍內船體板產生塑性變形,且沖擊波作用的圓形區域內部結構應變較小,結構產生圓盤狀拱起變形,與板格形成塑性鉸.
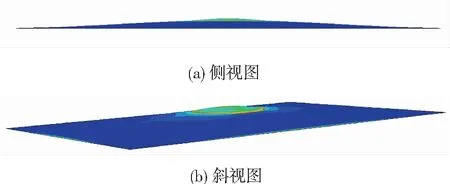
圖4 船體板架結構塑性變形
4.3 船體板架結構響應分析
圖5給出了1.2 ms時船體板架結構響應云圖.圖6給出了A、B、C、D這4個考核點的板架結構響應計算結果.從圖6可以看出,沖擊波傳播過程中,位移及加速度響應大小沿板格中心向外逐漸減小,離爆心最近的D點位移、加速度響應最大,而A點最小,即板架結構響應與距離爆心距離呈反比.
5 結 論
1)能夠實現對流場強間斷的高分辨率捕捉,對激波具有較高的分辨率,通過在間斷附近構造Riemann問題的方式,能有效的抑制界面附近非物理震蕩,并能消除間斷附近的數值耗散.
2)RKDG-GFM-LSM方法能很好的模擬近壁面水下爆炸沖擊波產生、傳播、反射和爆炸產物的膨脹等現象,并觀察到沖擊波傳播中的馬赫桿以及氣泡空化現象.船體板架結構水下爆炸模擬中發現,結構產生圓盤狀拱起變形,與板格形成塑性鉸,板架結構響應與距離爆心距離成反比.
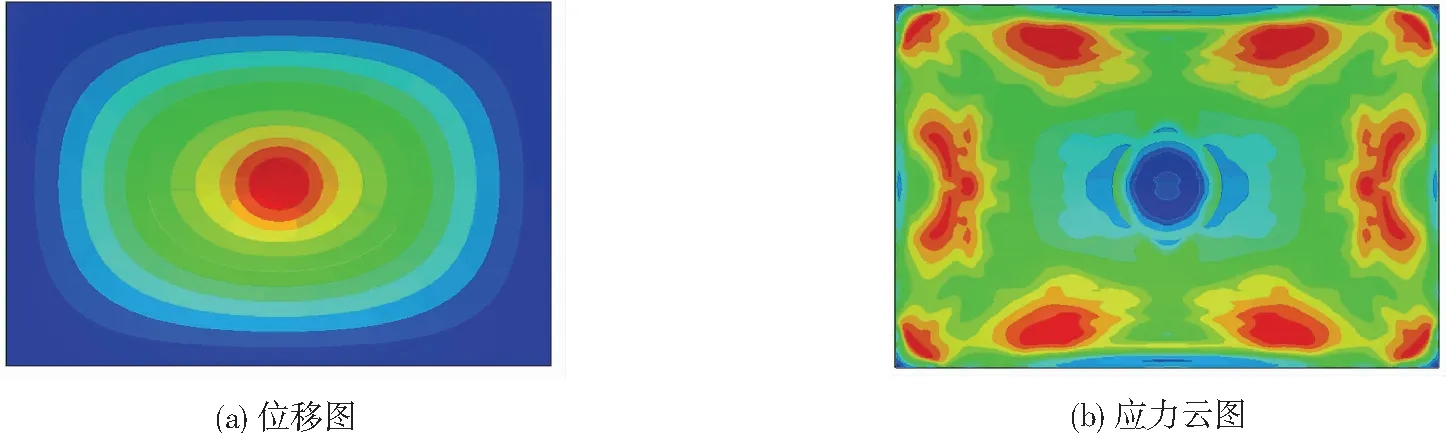
圖5 船體板架結構響應云圖
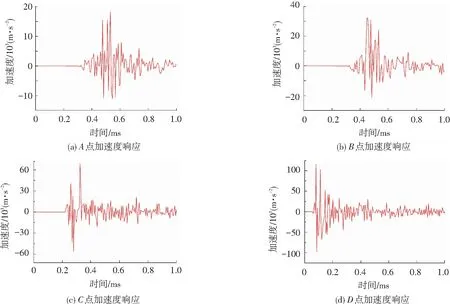
圖6 考核點位移、加速度響應時歷曲線
[1] SHIN Y S, SCHNEIDER N A. Ship shock trial simulation of USS Winston S. Churchill (DDG 81): modeling and simulation strategy and surrounding fluid volume effects[C]//Proceedings of the 74thShock and Vibration Symposium. San Diego, CA, Oct. : [s.n.], 2003: 27-31.
[2] 崔杰, 張阿漫, 郭君, 等. 艙段結構在氣泡射流作用下的毀傷效果[J]. 爆炸與沖擊, 2012, 32(4): 355-361.
[3] 崔杰. 近場水下爆炸氣泡載荷及對結構毀傷試驗研究[D]. 哈爾濱: 哈爾濱工程大學, 2013.
[4] SUSANTO A, IVAN L, De STERCK H, et al. High-order central ENO finite-volume scheme for ideal MHD[J]. Journal of Computational Physics, 2013, 250: 141-164.
[5] JEONG W, SEONG J. Comparison of effects on technical variances of computational fluid dynamics (CFD) software based on finite element and finite volume methods[J]. International Journal of Mechanical Sciences, 2014, 78: 19-26.
[6] QIU Jianxian, LIU Tiegang, KHOO B C. Simulations of compressible two-medium flow by runge-kutta discontinuous galerkinmethods with the ghost fluid method[J]. Communications in Computational Physics, 2008, 3(3): 479-504.[7] 張學瑩,趙寧,王春武. 可壓縮多介質流體數值模擬中的Level-Set間斷跟蹤方法[J]. 計算物理,2006, 23(5): 518-524.[8] JOHNSEN E. Numerical simulations of non-spherical bubble collapse: with applications to shockwave lithotripsy[D]. Pasadena: California Institute of Technology, 2008.
[9] 任少飛. 基于間斷迦遼金法的艦船水下及空中爆炸模擬[D]. 哈爾濱:哈爾濱工程大學, 2012.
[10]ZHU Jun, LIU Tiegang, QIU Jianxian, et al. RKDG methods with WENO limiters for unsteady cavitating flow[J]. Computers & Fluids, 2012, 57: 52-65.
[11]BILLET G, RYAN J, BORREL M. A Runge Kutta Discontinuous Galerkin approach to solve reactive flows on conforming hybrid grids: the parabolic and source operators[J]. Computers & Fluids, 2014, 95: 98-115.
[12]OSHER S, FEDKIW R P. Level set methods: an overview and some recent results[J]. Journal of Computational Physics, 2001, 169(2): 463-502.
[13]陳榮三. 大密度比和大壓力比可壓縮流的數值計算[J]. 應用數學和力學, 2008, 29(5): 609-617.
[14]BO W, GROVE J W. A volume of fluid method based ghost fluid method for compressible multi-fluid flows[J]. Computers & Fluids, 2014, 90: 113-122.
[15]HAAS J F, STURTEVANT B. Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities[J]. Journal of Fluid Mechanics, 1987, 181: 41-76.
(編輯 張 紅)
Numerical simulation of the response for Hull plates subjected to underwater explosion based on RKDG method
YU Fulin, GUO Jun, YAO Xiongliang, REN Shaofei
(College of Shipbuilding Engineering, Harbin Engineering University, 150001 Harbin,China)
In order to solve the underwater explosion flow field with large discontinuities, Level Set method was applied to track the interface position of the multi-medium flow, Ghost Fluid method was used to calculate the physical parameter of both sides of the interface, time and space were discretized by Runge-Kutta Discontinuous Galerkin Method, Euler equations of the flow field were solved. One-dimensional and two-dimensional assessments were conducted by RKDG approach. The results reflect the phenomena of underwater explosion shock wave generation, propagation, reflection and explosion products expansion. Finally, the shock responses and damage characteristics of hull plates under shock load were simulated with the nonlinear FEM softeware ABAQUS. The RKDG method can be applied to simulate the hull plates response with high accuracy. The response of hull plates is inversely proportional to the blast center distance.
underwater explosion; RKDG; shock load calculation; hull plates response; FEM; numerical simulation
10.11918/j.issn.0367-6234.2016.04.023
2014-11-26.
國家自然科學基金(51109042);中國博士后科學基金(2012M520707);黑龍江省自然科學基金 (E201124).
于福臨(1988—),男,博士研究生;
姚熊亮(1963—),男,教授,博士生導師.
姚熊亮,yaoxiongliang@163.com.
U663.2
A
0367-6234(2016)04-0139-05

