復雜工程地質體地應力場智能反演

楊志強，高 謙，翟淑花，楊 嘯

(1.金屬礦山高效開采與安全教育部重點實驗室(北京科技大學),100083 北京；2.金川集團股份有限公司, 737104 甘肅 金昌； 3.北京地質研究所,100120 北京)

?

復雜工程地質體地應力場智能反演

楊志強1,2，高 謙1，翟淑花3，楊 嘯1

(1.金屬礦山高效開采與安全教育部重點實驗室(北京科技大學),100083 北京；2.金川集團股份有限公司, 737104 甘肅 金昌； 3.北京地質研究所,100120 北京)

地應力是地質構造和自重共同作用在地質體內形成的原始應力，是影響工程穩(wěn)定性和災變失穩(wěn)的重要因素.由于受漫長的地質構造作用和地質演化，地應力場隨時間和空間變化，由此使準確反演地應力場造成困難.以金川礦區(qū)為工程背景，借助地應力測量結果，開展工程地質體的地應力場反演研究.首先,建立礦區(qū)工程地質體三維數(shù)值模型，并采用正交數(shù)值分析和遺傳規(guī)劃算法，建立地應力與巖體參數(shù)和側壓系數(shù)的函數(shù)關系；然后,根據(jù)實測的地應力值與計算的地應力值之差平方和最小為優(yōu)化目標，建立工程地質體的地應力場反演優(yōu)化模型.采用遺傳算法求解，獲得礦區(qū)巖體參數(shù)和側壓系數(shù)；最后,將其代入數(shù)值模型進行正分析由此獲得初始地應力場.通過4個測點地應力測量值與反演值對比分析可知，反演地應力的最大誤差為16%，最小誤差僅為0.62%.研究結果表明，地應力智能反演方法可用于復雜工程地質體的地應力場反演，且獲得的地應力場滿足地質工程分析所需要的精度.關鍵詞: 工程地質體；地應力場；智能反演;FLAC3D;遺傳算法

地應力是存在于地層中的天然應力，是導致工程變形破壞和地質災害的內動力，是地下工程穩(wěn)定性分析和災害防控必須考慮的重要因素之一[1-5].由于地質體在漫長的地質構造運動中經(jīng)歷多次地質作用和改造演化，在地層內封存不同時期的殘余應力，因此地質構造類型、作用程度和方向不同，導致地應力場的大小和方向存在時間和空間的變異性.由此給工程巖體的地應力場反演帶來極大困難，一直是巖土工程穩(wěn)定性分析長期研究而未能解決的技術難題，是地質工程研究的課題之一.

20世紀80年代首次提出黏彈性位移反分析法，根據(jù)圍巖變形監(jiān)測信息和理論分析方法進行巖體參數(shù)和地應力反演.但黏彈塑性位移反分析存在的多解問題一直未能得到很好解決[6].隨著人工智能的發(fā)展，基于神經(jīng)網(wǎng)絡與數(shù)值分析方法相結合的地應力反演研究取得進展，但該種地應力反演僅僅將有限的地應力測量樣本進行外延和非線性回歸，仍難以解決復雜工程地質體的真實地應力場反演問題[7-13].地應力現(xiàn)場測量是獲得地應力的重要手段之一，通常根據(jù)工程范圍、重要性以及復雜程度，開展有限的地應力測量工作，并在此基礎上進行統(tǒng)計回歸分析，由此獲得研究范圍內的地質體主應力大小和方向[14-19].但由于受時間和經(jīng)費限制，大部分工程地應力測量不僅數(shù)量有限，且受測量手段以及復雜因素影響，通常獲得地應力測試結果存在很大程度的離散性，由此給地應力研究和工程應用帶來很多困難，直接影響地質工程穩(wěn)定性的定量分析及工程優(yōu)化設計.研究發(fā)現(xiàn)，目前地質體地應力研究大多集中于有限地質體的統(tǒng)計回歸和宏觀規(guī)律.換句話說，通過有限個地應力測量或結合地質構造形跡分析，給出表征有限范圍內的地質體中的地應力特征(側壓系數(shù)和主應力方向).眾所周知，復雜地質體經(jīng)歷多次地質構造運動，在地質體內封存不同時期的構造應力，導致地應力場存在很大的變異性.以致實測的有限地應力信息難以真實表征實際地應力.

近年來考慮到工程地應力特征的復雜性，結合地質構造形跡以及圍巖變形破壞特征進行地應力場識別，是目前復雜地質體地應力研究的發(fā)展動向[20-23]，但該種方法還局限于定性分析.本文將利用有限個典型和可靠的地應力測量結果，采用數(shù)值分析與遺傳規(guī)劃相結合，建立地質體的巖體參數(shù)和側壓系數(shù)的優(yōu)化數(shù)值模型，直接反演復雜地質體的地應力場，而不是通過求得有限地質體的側壓系數(shù)和主應力方向來表征地應力特征.該方法能夠考慮復雜地質體的地應力場所固有的空間變異性，根據(jù)工程巖體的巖性進行地應力場分區(qū)反演.由此獲得工程巖體的地應力場能夠與工程巖體數(shù)值分析實現(xiàn)無縫連接，從而提高數(shù)值分析方法在地質工程中應用的實用性與可靠性.

1 工程地質體地應力場智能反演方法

1.1 地應力現(xiàn)場測量

采用地應力測量技術，獲得工程地質體內的n個地應力測點的地應力測量值為

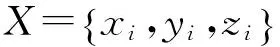
1.2 地應力影響函數(shù)建立

地質體中的地應力是在地質構造作用過程中，封存于巖體中的殘余應力，與區(qū)域構造應力和巖體特性密切相關.因此根據(jù)實測的n個地應力的測點位置(X={xi，yi，zi}T)，采用正交數(shù)值分析，建立地應力測點位置處的地應力與巖體參數(shù)和側壓系數(shù)的影響函數(shù).具體實施步驟如下.

1)建立三維數(shù)值分析模型.根據(jù)地質體的巖性和區(qū)域地應力構造特征，首先對地質體進行分區(qū)，然后利用三維數(shù)值分析系統(tǒng)(例如FLAC3D)，建立包含n個地應力測點的工程地質體三維數(shù)值模型.

2)正交數(shù)值分析設計.考慮地應力賦存條件與構造狀態(tài)，選擇影響地應力特征的因素和水平.考慮到地應力通常賦存于未受工程影響的原巖中，其巖體力學性質基本上處于彈性狀態(tài)，因此根據(jù)工程地質分區(qū)，選擇不同分區(qū)的巖體密度γi、彈性模量Ei和泊松比μi,i=1，m(其中m為工程地質體分區(qū)數(shù))以及水平方向的側壓系數(shù)λ1、λ2作為地應力分布特征的影響因素；借助工程經(jīng)驗或巖體分類，分別給出各個分區(qū)巖體的力學參數(shù)和地應力參數(shù)的變化范圍，由此確定地應力影響因素的設計水平.在此基礎上，采用正交設計表進行三維正交數(shù)值分析的方案設計.

1.3 建立地應力影響函數(shù)

以正交數(shù)值分析方案中的巖體參數(shù)和側壓系數(shù)作為自變量，以提取的地應力計算值作為因變量進行統(tǒng)計回歸或智能分析，建立地應力與巖體參數(shù)和側壓系數(shù)之間的函數(shù)關系為

1.4 建立地應力場反演優(yōu)化模型

(1)

2)確定地應力場反演優(yōu)化模型的約束條件.根據(jù)工程地質體的不同分區(qū)巖體參數(shù)和側壓系數(shù)的范圍，確定工程地質體地應力場反演優(yōu)化模型的約束條件為:

(2)

式中：γi、Ei分別為工程地質體第i個分區(qū)的巖體密度和彈性模量；λ1、λ2分別為三維數(shù)值模型的兩個水平方向的側壓系數(shù)；γi1，γi2分別為第i個分區(qū)的巖體密度上、下限；Ei1，Ei2分別為第i個分區(qū)的巖體彈性模量上、下限.

1.5 工程地質體地應力場反演優(yōu)化模型求解

考慮到地應力場反演優(yōu)化目標函數(shù)屬于高度非線性函數(shù)，因此采用遺傳算法對由式(1)和式(2)確定的優(yōu)化模型進行求解，由此獲得與原巖地應力場所對應的不同分區(qū)地質體的巖體參數(shù)和側壓系數(shù).

1.6 工程地質體的地應力場反演

將求解的工程地質體巖體參數(shù)和側壓系數(shù)，代入三維數(shù)值分析模型進行正分析，由此獲得的應力場即為工程地質體初始地應力場.

2 金川礦區(qū)工程地質體地應力場反演

為闡述基于有限個地應力測量值進行工程地質體地應力場反演方法，以金川礦區(qū)為工程背景進行實例分析.金川鎳礦是世界上著名的多金屬共生大型硫化銅鎳礦床，位于我國甘肅省河西走廊龍首山下長約6.5 km和寬約500 m的范圍內，已探明礦石儲量5.2×108t，鎳金屬儲量5.5×106t，列世界同類礦床第3位.金川銅鎳礦床地質構造特征主要表現(xiàn)以下兩個方面.

1)金川礦區(qū)是一座典型的高地應力礦區(qū)，表現(xiàn)在礦體埋藏深，自重應力大，近似水平方向的構造應力最高達到50 MPa，即水平應力是垂直應力的1.69～2.27倍.

2)金川礦床賦存于海西期含礦超基性巖體中，上盤圍巖為二輝橄欖巖，下盤圍巖主要為大理巖和二輝橄欖巖.礦區(qū)內斷裂構造極其發(fā)育，F(xiàn)16、F15、F26等斷層對礦巖條件產(chǎn)生劇烈影響，使礦巖異常破碎，表現(xiàn)出巖石強度高而巖體穩(wěn)定性差的特征，由此給采礦方法選擇和采場地壓控制帶來不利影響.

為優(yōu)化采礦設計和實現(xiàn)對采場地壓優(yōu)化控制，金川鎳礦開展了不同階段的地應力測量，獲得大量的地應力測量結果[24].根據(jù)金川龍首礦和二礦區(qū)地應力測量結果，建立包含兩個礦區(qū)工程地質巖體的三維數(shù)值分析模型，進行金川礦區(qū)地應力場反演,如圖1所示.

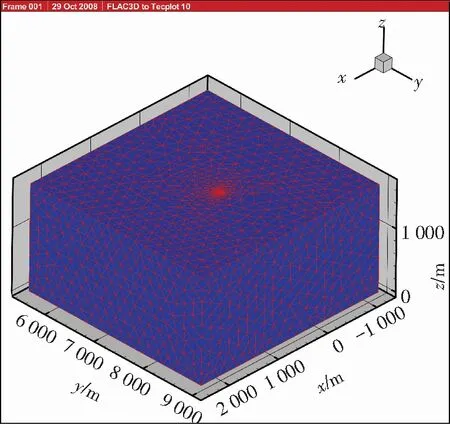
圖1 金川礦區(qū)地質體地應力場反演三維數(shù)值模型

2.1 金川礦區(qū)地應力測量

根據(jù)金川礦區(qū)地應力測點位置、埋深、巖性以及地應力測量結果[24]，選擇表1中9個地應力測試數(shù)據(jù)，用于金川礦區(qū)地應力反演.其中前5個數(shù)據(jù)用于建立優(yōu)化模型，后4個數(shù)據(jù)用于檢驗地應力場反演結果.

表1 金川礦區(qū)地應力測點位置和實測地應力值

2.2 建立金川礦區(qū)地應力影響函數(shù)

2.2.1 建立金川礦區(qū)工程地質體數(shù)值分析模型

為了建立金川礦區(qū)地應力影響函數(shù)，首先建立金川礦區(qū)工程地質體三維數(shù)值模型.三維數(shù)值模型坐標系統(tǒng)為：水平面指向東為x坐標，指向北為y坐標，垂直向上為z坐標(見圖1).

2.2.2 工程地質體分區(qū)與巖體參數(shù)選擇

考慮到礦巖體物理力學性質存在顯著差異，根據(jù)力學特性劃分成礦體和巖體兩個分區(qū)，分別采用γ1，E1，μ1和γ2，E2，μ2表示礦巖體密度、彈性模量和泊松比.根據(jù)金川礦區(qū)已開展工程地質研究，確定礦巖體密度分別為2.8～3.6 t/m3和2.4～2.8 t/m3.礦巖體彈性模量分別為20～34 GPa 和6～20 GPa；礦巖體泊松比分別為0.20～0.24和0.20～0.26.根據(jù)金川礦區(qū)地應力實測結果，確定金川礦區(qū)x、y水平方向的側壓系數(shù)分別為0.5～1.2和1.1～1.5.

2.2.3 地應力影響因素和試驗水平及正交數(shù)值分析

選擇礦體和巖體參數(shù)γ1，E1，μ1，γ2，E2，μ2和礦區(qū)側壓系數(shù)λ1、λ2共8個因素和兩個水平進行金川礦區(qū)地應力場反演.表2給出了8因素2水平地應力場反演三維正交數(shù)值分析的因素與水平，表3給出了金川礦區(qū)地應力場反演三維正交數(shù)值分析的計算方案.

表2 金川礦區(qū)地應力反演的三維正交數(shù)值分析因素和水平

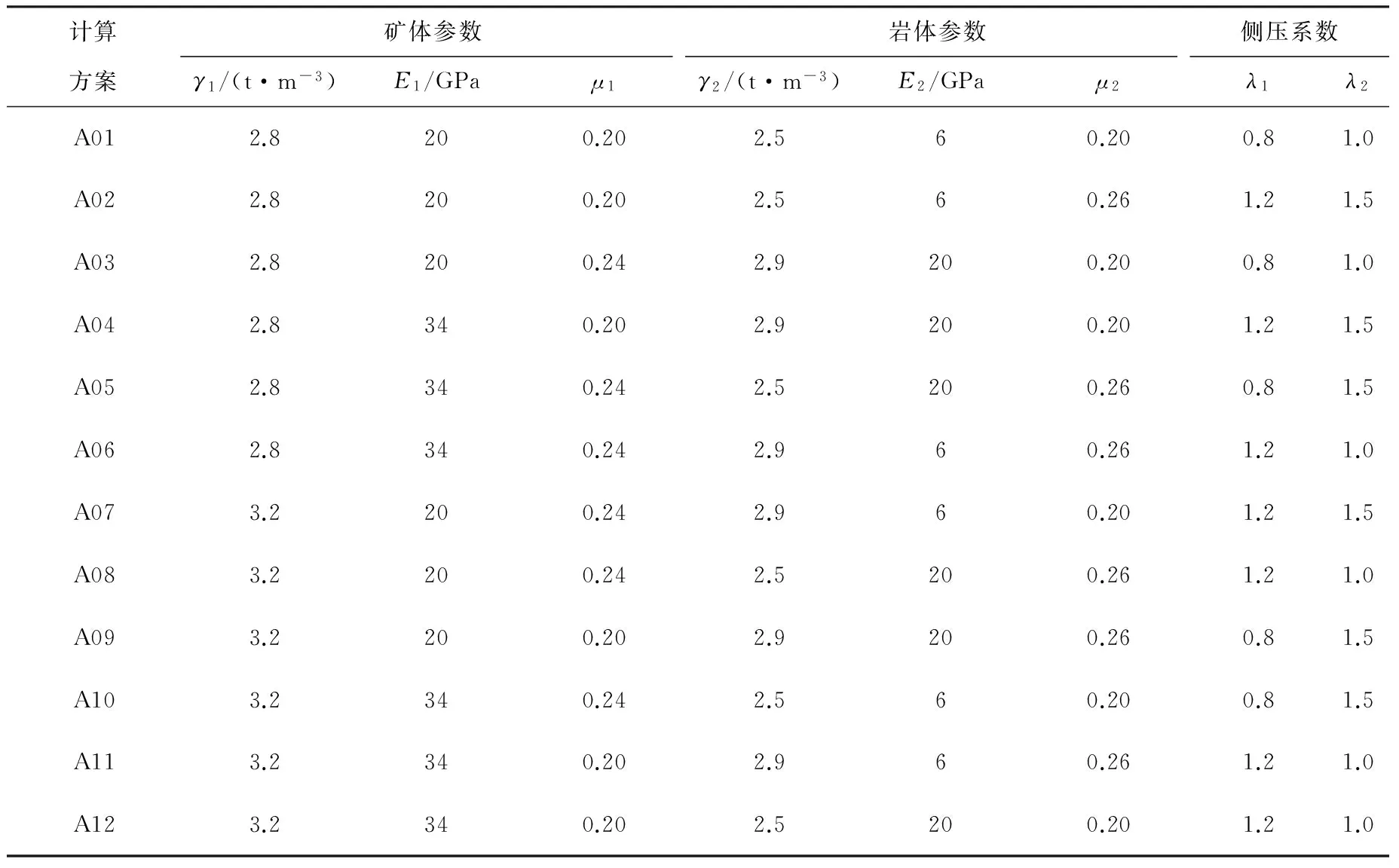
表3 金川礦區(qū)地應力反演的三維正交數(shù)值分析計算方案

2.2.4 金川礦區(qū)地應力測點地應力數(shù)值分析結果

根據(jù)圖1所示的金川礦區(qū)三維數(shù)值分析模型和表3的正交數(shù)值計算方案進行12次數(shù)值分析.在每次計算結果中提取三維數(shù)值分析模型的地應力測點處的地應力計算值，由此獲得如表4所示的礦區(qū)地應力各測點處的3個主應力大小和主應力方向.

2.2.5 建立地應力測點處的地應力影響函數(shù)

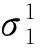
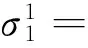
mydivide(x7，minus(x4，mydivide(mydivide(x7，x5)，plus(x6，ex3)))))，plus(x2，times(x2，mydivide(minus(x8，times(plus(x6，x6)，minus(x5，x3)))，mydivide(mydivide(x5，x7)，x7))))))，

minus(mydivide(times(mydivide(minus(plus(x7，x8)，plus(x7，plus(times(x2，x7)，x2)))，x8)，x3)，mydivide(x1，x7))，plus(mydivide (mydivide(x7，ex8)，plus(x6，x2))，mydivide(minus(x2，x8)，x4)))).

(3)

式中：xi(i=1,8)分別為礦體參數(shù)γ1,E1,μ1、巖體系數(shù)γ2,E2,μ2和側壓系數(shù)λ1,λ2.

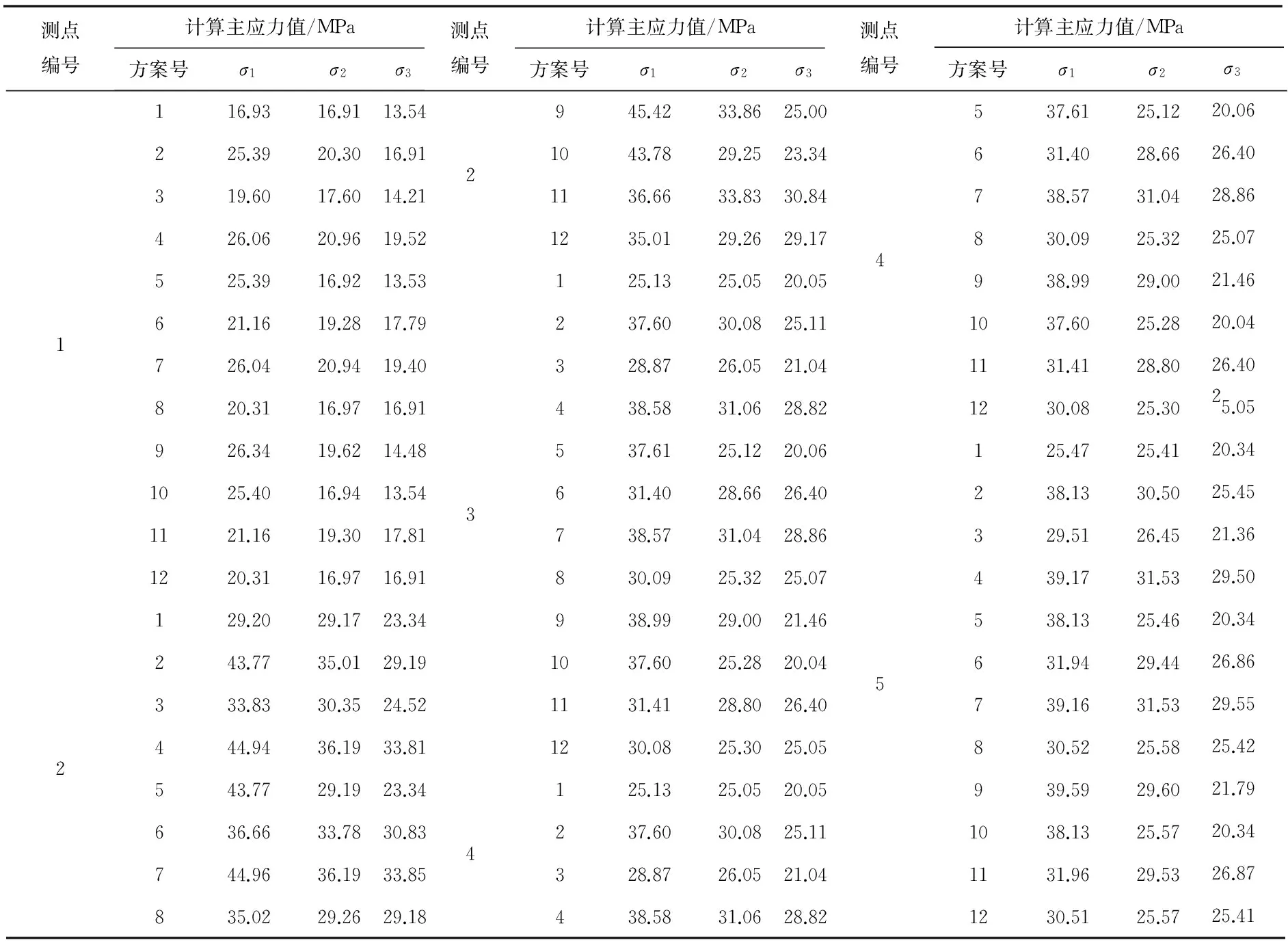
表4 金川礦區(qū)地應力測點處的地應力數(shù)值計算結果

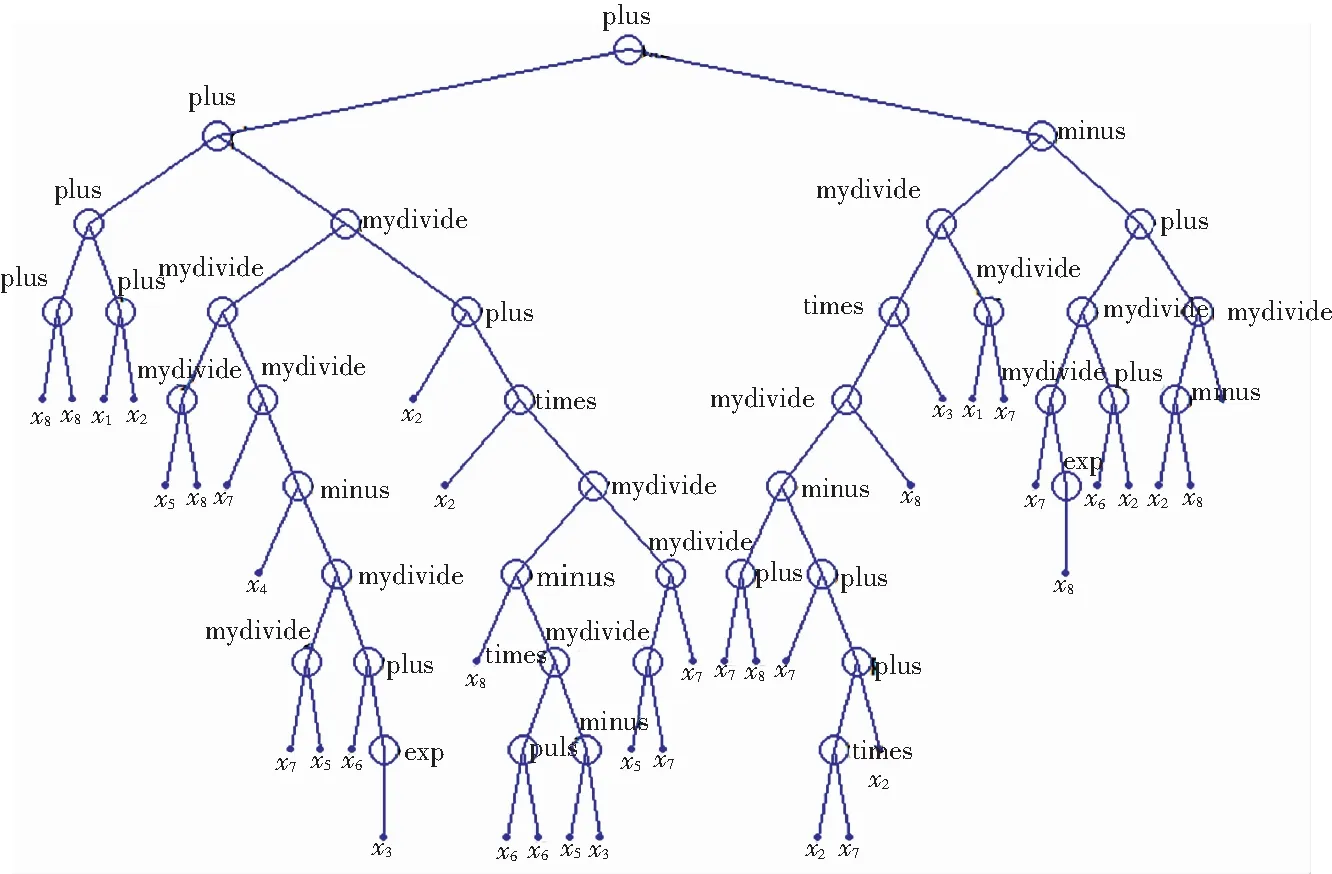
圖2 金川礦區(qū)地應力測點1位置的σ1的最佳遺傳樹

2.3 金川礦區(qū)地應力場智能反演優(yōu)化模型

基于金川礦區(qū)地質體中5個地應力測點處的地應力函數(shù)與實測地應力值之差的平方和最小為優(yōu)化目標，由此建立礦區(qū)地應力場反演優(yōu)化模型.

2.3.1 金川礦區(qū)地應力場反演目標函數(shù)

根據(jù)金川礦區(qū)地應力的遺傳規(guī)劃函數(shù)關系，建立地應力場智能反演目標函數(shù)為

((x8-x2x7-x2)/x8x3/x1x7-x7/ex8/(x6+x2)-(x2-x8)/x4-25.8)2+((x6+(x6+x1)x7)x7+

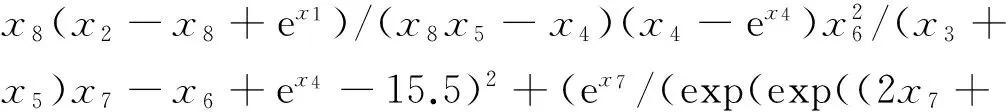
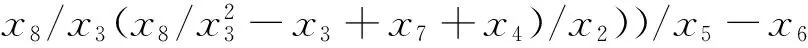
(x4+x8)x4)/x7/x5)/x2-13.0)2+((ex8+((ex8+(x8/e(x5+x6+x4/x5)+x6)e(x3/ex3/ex7)/(x1+exp(ex7))-

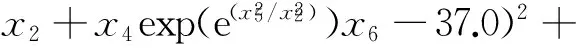
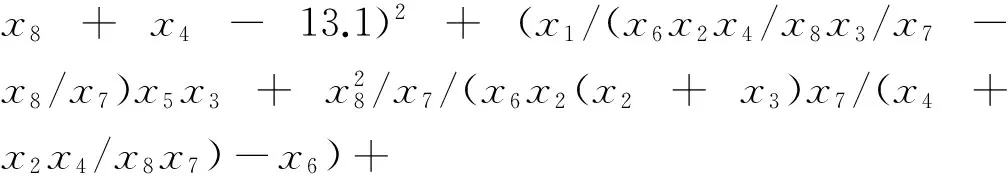
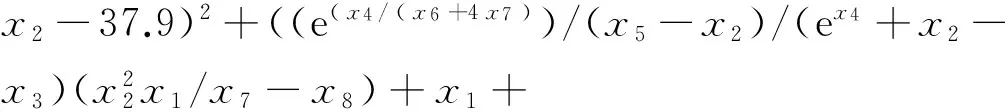
(x6+x2-x4/(x7-2x6)/(x2-x7-x5-x1-x1/(x1-x7)-x2x3)-(x2-x4+(x2-x8)/(x1-x2)+x2x3-x5-x7-x8-x3/(x2-2x7-x5-x1-x1/x5x8(x2+x3)-x7/(x4-x7/x4-x2x3-x2)))x3-12.2)2+

((x2/(x7-x1+1)+x8/x7+ex1/x6x8+x1+(x5/x2x8+x5/x6x8+x7+x2/x8)/(x7-x1+x2/x4))/(x7-x1+x2/x8)+x8+x3/(x5-x2)x2x7+x2-31.6)2+(x4/x3+x8/(x7+x5/ex8)+(((2x8/x3+x3/(x6+x7)+x7+(2x1+x8)/x8+2x4)/x2+x8)/x3+x2x3+(ex1(x1+x5/ex8+x8)+x4)/x2+2x1+x4)/x2/x3+

x2/x1-18.7)2+(x2-(((x2-(x7+x4)x1-x8)x8-x1+(x2+(x2-2x8-x6)x8-(x1+(x1+x8)x6)(x1+(x6+x8)x6))x6)x8+(x2+(x2-ex7x2x6+x5)x8-(x1+(x5x6+x8)(x1+(x6+x8)x6))e(x8x7))x6)x6+(ex3+x4)x8-11.6)2.

(4)

2.3.2 金川礦區(qū)地應力場反演約束條件

根據(jù)金川礦區(qū)礦體和巖體參數(shù)以及地應力的變化范圍，由此確定優(yōu)化模型的約束條件為：

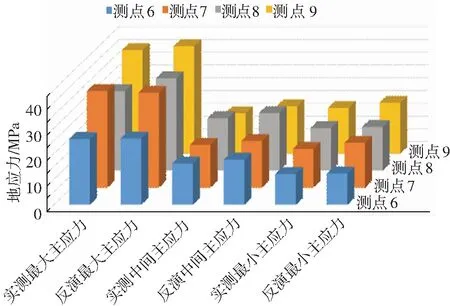
6

0.20<μ1<0.26，0.20<μ2<0.24；

2.4 金川礦區(qū)地應力場反演優(yōu)化模型求解

利用遺傳算法的全局搜索能力，求解由目標函數(shù)式(3)和約束條件式(4)確定的地應力反演優(yōu)化模型.首先設置遺傳算法的參數(shù)見表5；然后進行遺傳算法操作：即隨機產(chǎn)生初始群體→個體適應度評價→選擇操作→交叉操作→變異操作→終止法則(最大遺傳代數(shù))；最后獲得與礦區(qū)地質體初始應力場相匹配的礦、巖體參數(shù)和礦區(qū)側壓系數(shù)見表6.

表5 遺傳算法參數(shù)表

表6 金川礦區(qū)礦、巖體參數(shù)和側壓系數(shù)反演結果

2.5 金川礦區(qū)工程地質體地應力場反演

3 金川礦區(qū)地應力場反演結果誤差分析

為檢驗地應力場反演結果的可靠性，表7給出金川礦區(qū)4個測點的地應力實測值與反演值和誤差分析結果.圖3顯示了金川礦區(qū)6～9號測點的實測地應力值與反演地應力值的對比曲線.由此可見，采用本文的地應力反演方法獲得的3個主應力值與實測主應力值的誤差最大為17.98%，最小為0.62%.可見該地應力場反演方法具有一定的可靠性.

表7 金川礦區(qū)4個點實測地應力值與反演地應力值的對比分析

圖3 金川礦區(qū)4個測點實測地應力值與反演地應力值對比結果

4 結 論

1)地質體中的原巖應力是時間和空間的函數(shù)，是巖體物理力學參數(shù)的高度非線性函數(shù)，因此，采用遺傳規(guī)劃的遺傳樹結構，能夠表征地應力的非線性關系；考慮到地應力反演的優(yōu)化目標函數(shù)屬于高度非線性函數(shù)，利用遺傳算法的快速尋優(yōu)技術，能夠獲得目標函數(shù)的最優(yōu)解.

2)采用本文地應力反演方法，進行4個測點的主應力反演，并將反演結果與實測值對比，其最大誤差為17.98%，最小誤差為0.62%.考慮到地應力復雜特征及地應力測量存在的誤差，地應力反演誤差滿足地質工程分析的精度，該方法可為復雜地應力場反演和工程穩(wěn)定性分析提供一條途徑.

[1] 司光曄，張嚴. 基于地應力測試的公路巖爆預測技術研究[J]. 公路, 2013, (6): 256-261.

[2] 周垂一, 李軍, 嚴鵬. 錦屏二級水電站深埋隧洞施工難點解析[J]. 隧道建設, 2013, 33(6): 481-488.

[3] 馬行東.某電站樞紐區(qū)地下洞室?guī)r爆的特征與預防措施[J]. 水電站設計, 2013, 29(1): 63-65.

[4] 劉月鋒,衛(wèi)栓緊. 深部開拓巷道巖爆防治技術[J]. 建井技術,2013, 34(2):13～15

[5] 楊旭旭,靖洪文,陳坤福,等. 深部原巖應力對巷道圍巖破裂范圍的影響規(guī)律研究[J]. 采礦與安全工程學報, 2013, 30(4):495-500.

[6] 廖椿庭, 施兆賢.金川礦區(qū)原巖應力實測及在礦山設計中的應用[J]. 巖石力學與工程學報, 1983, 2(1): 103-112.

[7] 蔡美峰,喬蘭,于波, 等.金川二礦區(qū)深部地應力測量及其分布規(guī)律研究[J].巖石力學與工程學報, 1999，18(4): 414-418.

[8] 蔡美峰,劉衛(wèi)東,李遠. 玲瓏金礦深部地應力測量及礦區(qū)地應力場分布規(guī)律[J]. 巖石力學與工程學報, 2010, 29(2): 227-233.

[9] 康紅普, 林健, 張曉, 等. 潞安礦區(qū)井下地應力測量及分布規(guī)律研究[J]. 巖土力學, 2010, 31(3): 827-831.

[10]羅超文,李海波,劉亞群. 深埋巷道地應力測量及圍巖應力分布特征研究[J].巖石力學與工程學報,2010, 29(7):1418-1423.

[11]豐成君,陳群策,譚成軒, 等. 廣東核電站地應力測量及其應用[J]. 巖土力學, 2013,34(6):1745-1752.

[12]李云鵬,王芝銀. 粘彈性位移反分析的邊界元法[J].西安礦業(yè)學院學報,1989, (1):17-23.

[13]郭鋒,馬震岳,金長宇. 抽水蓄能電站地下洞室初始地應力場反演分析-基于神經(jīng)網(wǎng)絡和快速拉格朗日算法[J]. 地下空間與工程學報, 2007, 3(2):208-212.

[14]賈善坡,陳衛(wèi)忠,譚賢君,等. 大崗山水電站地下廠房區(qū)初始地應力場Nelder-Mead 優(yōu)化反演研究[J].巖土力學, 2008, 29(9): 2341-2349.

[15]岳曉蕾,李術才,陳啟輝,等.多元多方程地應力反演與工程應用研究[J].山東大學學報:工學版, 2010, 40(2): 66-70.

[16]張國強,王桂萱. 基于神經(jīng)網(wǎng)絡結構分解與FLAC3D的初始地應力場反演[J].大連大學學報, 2007, 28(6):43-47.

[17]楊志雙,潘懋.基于遺傳算法(GA)的地應力有限元反演研究[J]. 水文地質工程地質, 2006, 33(2):80-83.

[18]王福玉,高謙,張周平.金川礦區(qū)地應力規(guī)律與人工神經(jīng)網(wǎng)絡預測研究[J]. 巖石力學與工程學報, 2003, 22(S2): 2601-2606.

[19]羅潤林,阮懷寧,黃亞哲,等.巖體初始地應力場的粒子群優(yōu)化反演及在FLAC3D中的實現(xiàn)[J]. 長江科學院院報, 2008, 25(4):73～76.

[20]張貴慶. 三峽地下廠房區(qū)地應力場反演分析[J]. 水利與建筑工程學報, 2011, 9(4):66-71.

[21]張延新, 蔡美峰. 地應力場與地質構造運動關系研究[J]. 銅業(yè)工程, 2004, (3):7-9.

[22]江權,馮夏庭,徐鼎平,等.基于圍巖片幫形跡宏觀地應力估計方法探討[J].巖土力學, 2011, 32(5):1452-1459.

[23]張宜虎,盧軼然,周火明,等.圍巖破壞特征與地應力方向關系研究[J]. 巖石力學與工程學報, 2010, 29(S2): 3526-3535.

[24]楊志強, 高謙, 王玉山,等. 特大型鎳礦工程地質與巖石力學[M].北京:科學出版社, 2013.

(編輯 張 紅)

Intelligent inversion method of in-situ stress field for a complicated engineering geological body

YANG Zhiqiang1,2，GAO Qian1，ZHAI Shuhua3，YANG Xiao1

(1.Key Laboratory of High-Efficient Mining and Safety of Metal Mines(University of Science and Technology Beijing), Ministy of Education,100083 Beijing, China; 2.Jinchuan Group Co. LTD. 737104 Jinchang, Gansu, China; 3.Beijing Institute of Geology, 100120 Beijing,China)

The in-situ stress is the original stress in the geological body forming from the geological structure and gravity. It is an important factor which influences the stability and instability of the geological engineering. Due to the long geological tectonic setting and geological evolution, the in-situ stress field is a function of time and space, thus it is very difficulty for us to make accurate inversion the in-situ stress field. Taking Jinchuan mine as the engineering background and with the aid of in-situ stress measurement in Jinchuan mine, the in-situ stress field was inverted. First the 3D numerical mode of geological engineering body in Jinchuan mine was established, and the relation between in-situ stress and rock mass parameters and coefficients of horizontal pressure was obtained by orthogonal numerical analysis and genetic programming(GP). Then the optimization mode was established which takes the sum of squares of differences between the measured initial stress and calculation initial stress up to the minimum value as the objective function. The rock masses parameters and coefficients of horizontal pressure would been obtained by solving the optimization model using genetic algorithm. Finally, the initial stress field can be obtained when the 3D numerical analysis is carried out again by inputting the parameters of rock masses and coefficients of horizontal pressure. Based on comparing inverting in-situ stress with the measured values for the 4 gauging points, the maximum and minimum error of the principal stress is 16% and 0.62% respectively. The results show that the method of intelligent inversion of in-situ stress field can be applied for complicated geological engineering body to simulate in-situ stress field and the accuracy meets the engineering demand.

engineering geological body；in-situ stress field；intelligent inversion;FLAC3D;genetic algorithm

10.11918/j.issn.0367-6234.2016.04.026

2014-09-14.

國家重點基礎研究發(fā)展計劃(973計劃)(2010CB731501).

楊志強(1957—)，男，教授級高工，博士生導師;

高 謙(1956—)，男，教授，博士生導師.

高 謙,gaoqian@ces.ustb.edu.cn.

TU431

A

0367-6234(2016)04-0154-07