從兩個教學片斷審視課堂生成

蔡友山

摘要：在初中數學教學中，教師不拘泥于預設，并能智慧地處理好預設與生成的關系，生成才能更加精彩，才能使數學課堂更具有活力，才能使課堂教學效率達到最大值。在初中數學教學中，教師要注重知識的形成過程，善于利用問題引發學生的數學思考，鼓勵學生的創造性思維，充分體現學生的主體地位，真正實現學生的學與教師的教的統一。

關鍵詞：教學片段 教學預設 課堂生成精彩 積淀

在初中數學教學中，教師處理好預設與生成的關系，是提高課堂教學效益的關鍵所在。教學過程的生成性對教學預設提出了更高的要求。每位教師只有創造性地使用教材、全面地了解學生和有效地開發課程資源，預設才能富有成效。同時，在初中數學教學中，教師只有不拘泥于預設，并能智慧地處理好預設與生成的關系，生成才能更加精彩，才能使數學課堂更具有活力，課堂教學效率才能達到最大值。

一、自然生成。成就課堂精彩

對于浙教版（七上）教材“7。7相交線”，在教學時，我對例1做了如下改動：

原題：如圖1（原圖7—37），3條直線相交于一點O，說出圖中的6組對頂角。

改動：如圖1，3條直線相交于一點O，圖中有幾組對頂角？

改動意圖：解題目標的變化，勢必導致解題思維方式的變化。前者目標是“找6組對頂角”，側重點停留在“找”，且有數量“6”的限制。學生解決問題的思路具有明確的導向性，不利于學生思維的發散。相反，后者為學生提供了更加廣闊的思維空間。

教學片段1：

學生A：有4組。

學生B：不對，有5組。

學生C：應為6組。

教師：還有其他結果嗎？請這3個同學講講自己的理由。

A同學走上講臺用不同顏色的粉筆畫出4組對頂角。

臺下很多同學：還漏掉了2組。

教師：誰上來畫出漏掉的2組。

學生D走上講臺畫出漏掉的2組。

教師：看來，數圖形的個數需要仔細認真，力求做到不重不漏。

學生E：我有更簡單的方法確定對頂角的組數。

教師：我們用熱烈的掌聲請E同學上臺發表高見。

學生E：如圖2，兩條相交直線，我們稱之為一個基本圖形，其中有2組對頂角。如圖3，因為圖中任何兩條直線都構成一個新的基本圖形，根據“二合一原理”，構成基本圖形的總個數為2×3=6。由此可知，其中有2×3=6組對頂角。（師生驚訝，并給予長時間熱烈的掌聲）

教師：E同學解法新穎，講解清楚明了，值得大家學習。用此法，不用一一畫出這些對頂角。只要知道直線的條數，就容易計算出對頂角的組數。

教師：請同學們用E同學的方法分組討論兩個問題：（1）如圖4，5條直線相交于同一點，其中包含幾個基本圖形？有幾組對頂角？（2）n條直線相交于一點，其中包含幾個基本圖形，有幾組對頂角。（分組討論5分鐘左右）

教師：請同學們分組展示討論結果。（每組派一個代表發言）……

二、精彩的生成。源自課堂積淀

您讀到這里，難免會產生一絲困惑：學生E為什么會有如此奇妙的解法？“二合一原理”又是什么新鮮事物？下面的教學片斷或許能為您揭開謎底。（說明：片斷2是在片斷1之前的一節習題課）

教學片段2：

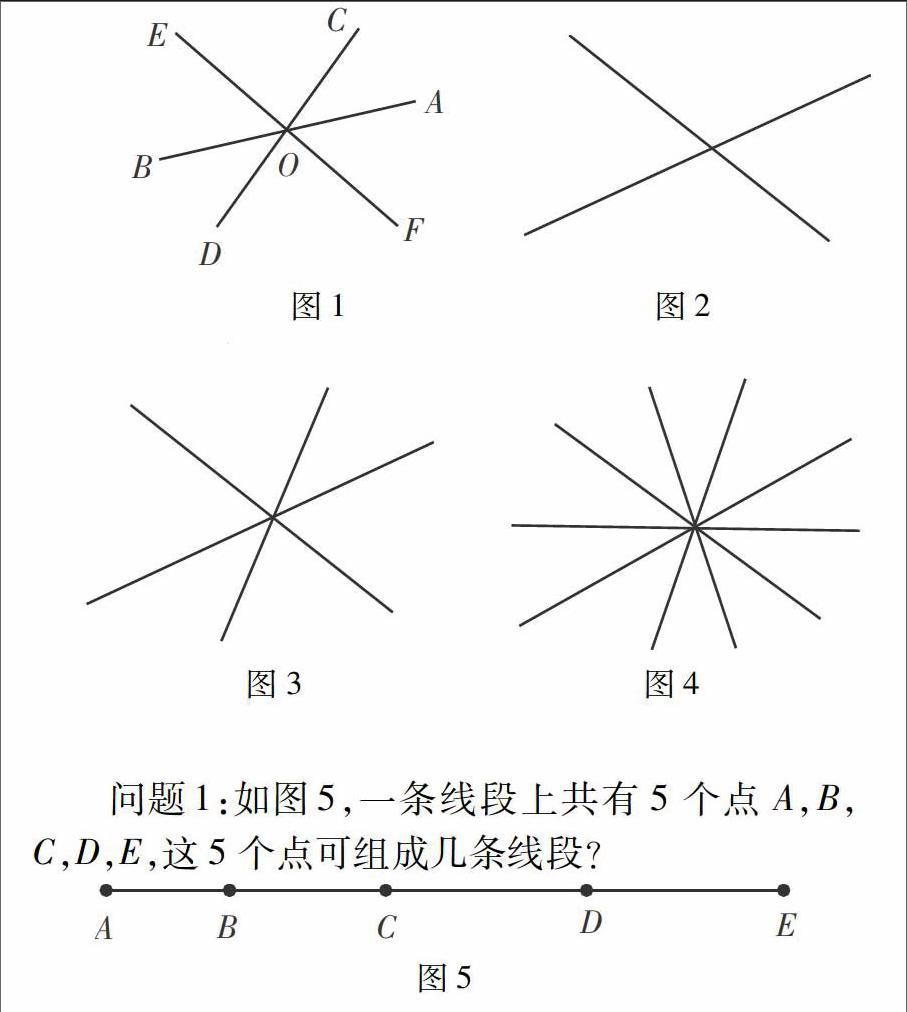
問題1：如圖5，一條線段上共有5個點A，B，C，D，E，這5個點可組成幾條線段？

學生A：10條。

教師：能說說你的理由嗎？

學生A：以A為端點的線段有：AB，AC，AD，AE，共4條；以日為端點的線段還有：BC，BD，BE，共3條；以C為端點的線段還有：CD，CE，共2條；以，D為端點的線段還有：DE，1條。所以，共有線段4+3+2+1=10（條）。

教師：以B為端點的線段不是還有BA嗎，你為什么沒有把它算進去？

學生A：因為線段AB與線段BA是同一條線段，不能重復計數。

教師：說得好！在分類計數時，我們一定要做到不漏不重。

教師：剛才這位同學用枚舉法把所有線段都一一列舉出來，這是解決計數問題的一種好方法。還有其他方法解決這個問題嗎？

學生B：因為以A為一個端點的線段有4條，同樣以B，C，D，E為一個端點的線段都有4條，因此線段的總條數為4×5，但每條線段都重復計數一次，所以線段的總條數為1/2×4×5=10。

教師：這種方法很有新意，而且非常簡捷。現在請大家選擇一種方法解決下面的問題。

問題2：如圖6，從同一端點O出發的5條射線OA，OB，OC，OD，OE，可組成幾個角？

問題3：如圖7，過平面內的5個點A，B，C，D，E，最多可畫幾條直線？

問題4：如圖8，平面內有5條直線a，c，d，e，它們最多有幾個交點？

學生：獨立完成，選代表展示。（結果都是4+3+2+1=10）

教師：它們的結果為何如此相似？你能否從這4個問題的本質上進行分析說明？（提示：這4個問題有什么共同點？）

經過教師的提示，學生七嘴八舌地說開了，教師把同學們的想法進行提煉板書：

問題1：任意兩點構成一條新的線段。

問題2：任意兩條射線組成一個新的角。

問題3：任意兩點構成一條新的直線。

問題4：任意兩條直線產生一個新的交點。

教師：我們發現，這4個問題有著共同的特征，不妨歸納為：對于n個元素，如果其中任意兩個元素都能構成一個新元素，那么構成新元素的總個數為（n-1）+（n-2）+…+2+1=1/2（n-1）n（個）。

學生：原來如此。

教師：為了方便記憶，我們不妨稱之為“二合一原理”。你能舉出一些生活中的“二合一”問題嗎？

學生：握手問題，單循環賽問題，等等。

三、反思

1.合理利用生成性資源，提高課堂教學的有效性

教學方案是教師對教學過程的預設，實施教學方案，是把預設轉化為實際的教學活動。在這個過程中，師生雙方的互動往往會生成一些新的教學資源，如新情境、新問題、新思路、新方法、新結果等。這就需要教師能夠及時把握，因勢利導，適時調整預案，使教學活動達到更好的效果。正如片斷1，學生E提出了與眾不同的解決問題的新方法，這顯然超出了教師的預設，但教師及時捕捉了這一思維火花，并把它轉化成生成性資源，通過教師的肯定、總結，學生的強化訓練，把這一資源的作用發揮到極致，提高了課堂教學效率。這就是教師的智慧，也是教師追求的教學境界。

2.整合多元知識，為課堂生成提供原動力

片斷2是一節習題課，教師沒有就題講題，而是把同類問題羅列出來，讓學生經過觀察、比較，發現它們的共同特征，從本質上弄清了“它們的結果為何如此相似？”不僅如此，教師還創造性地總結出“二合一原理”，實現了多元知識的整合，使原本零散的知識點得到“歸一”，這是中國古代教學思想“由博返約”的體現。在這個過程中，教師十分注重知識的形成過程，善于利用問題引發學生的數學思考，鼓勵學生的創造性思維，充分體現了學生的主體地位，真正實現了學生的學與教師的教的統一。也正因為片斷2的積淀，才會出現片斷1的精彩，這是知識的遷移，更是能力的提升。