基于最優Morlet小波自適應包絡解調的弱故障特征提取方法

侯新國， 牛超， 楊忠林

(海軍工程大學 電氣工程學院，湖北 武漢 430033)

?

基于最優Morlet小波自適應包絡解調的弱故障特征提取方法

侯新國， 牛超， 楊忠林

(海軍工程大學 電氣工程學院，湖北 武漢 430033)

為自適應實現Morlet小波與故障沖擊特征成分的最優匹配，采用基于Shannon小波熵的方法優化帶寬參數設計最優Morlet小波。針對最佳尺度求取的難題，利用譜峭度與小波熵均能敏感反映沖擊性的特性，提出了基于峭熵比求取最佳尺度。基于此，提出基于最優Morlet小波自適應包絡解調的弱故障特征提取方法，該方法首先對信號進行最優Morlet連續小波變換；然后，依據峭熵比自適應地求取最佳尺度并提取最佳尺度的小波系數；最后，對最佳尺度的小波系數取模即可實現對最優頻帶的包絡解調，得到包絡譜，從而實現微弱故障特征的提取。實例分析表明：該方法克服了傳統包絡解調需要人為設定帶通濾波器參數的不足，能有效地從強噪背景中提取微弱故障特征。

最優Morlet小波；自適應包絡解調；Shannon小波熵；故障特征；峭熵比

0 引 言

電機軸承的早期故障，因其故障特征很微弱，常常淹沒于強背景噪聲中。包絡解調法是目前滾動軸承故障診斷中最常使用的方法之一[1-2]。在對故障振動信號進行包絡解調前，通常要對信號進行帶通濾波。然而，帶通濾波的實現需要人為選擇濾波中心頻率與帶寬，應用極為不便[3]。小波分析方法在振動信號包絡解調中得到廣泛應用[4]。Morlet小波是故障診斷領域中常用的一種小波[5-6]，文獻[7]采用基于Morlet小波的連續小波變換的包絡檢波算法提取淹沒在噪聲中的故障特征，取得一定效果，但該方法未考慮到Morlet小波的優化，不能自適應實現對沖擊成分的最優匹配，使得包絡解調效果不佳。利用最小Shannon小波熵自適應優化帶寬參數來設計與沖擊特征成分相匹配的Morlet小波，是優化小波變換算法的一種新思路，但最佳變換尺度的求取是基于Morlet小波分析的難點。文獻[5]、文獻[8]采用小波變換系數矩陣的奇異值比譜(singular value ratio,SVR)求取最佳尺度,該方法在利用SVR探測信號的周期分量時，存在截斷誤差導致其經常失效。由于譜峭度和Shannon小波熵均能反映強噪聲背景下沖擊信號的特征，提出基于譜峭度與Shannon小波熵比值即峭熵比(kurtosis entropy ratio,KER)的方法求取最佳變換尺度，以克服上述最佳尺度求取方法的缺陷。在此基礎上，為了有效提取強噪聲背景下的微弱故障特征和克服傳統包絡解調方法的不足，提出基于最優Morlet小波自適應包絡解調的弱故障特征提取方法。該方法首先依據信號的特點自適應地設計最優Morlet小波，并利用最優Morlet連續小波變換對信號進行全頻段帶通濾波；然后依據峭熵比自適應地獲取最優頻帶；最后對最優頻帶小波系數取實部，并對其求模，即可獲得最優頻帶的包絡實現包絡解調。

1 基于Morlet小波變換的包絡解調原理

Morlet小波的定義式為

(1)

其傅里葉變換為

Φ(f)=e-π2fb(f-fc)2。

(2)

式中：fc為小波的中心頻率；fb為帶寬參數，fb越小，波形衰減越快，帶寬越寬，直至逼近一個脈沖信號；fb越大，則波形衰減越慢，帶寬越窄，最后退化成一個余弦信號。因此，在應用Morlet小波進行故障診斷時，需要優化fb，以實現小波與沖擊特征成分的最優匹配。

由式(2)，經傅里葉逆變換知小波φ(t)的實部φR(t)和虛部φI(t)分別是t的實偶函數與實奇函數，因此它們的頻譜ΦR(f)和ΦI(f)分別是實偶函數和純虛奇函數。由于Morlet小波頻譜函數僅含有正頻率部分，故Morlet小波是解析小波。于是可推知ΦR(f)和ΦI(f)滿足下列關系

ΦI(f)=-jsgn(f)ΦR(f)。

(3)

式中sgn(f)為符號函數。上式是一個時間函數Hilbert變換式的等價頻域表示，即式(3)表明φI(t)是φR(t)的Hilbert變換。

(4)

因此有

(5)

又由

φI(t)=H[φR(t)]。

(6)

得

(7)

其中,H[?]表示Hilbert變換運算，因此有

(8)

2 基于Shannon小波熵自適應設計最優Morlet小波的方法

Shannon小波熵[6,9]定義為

(9)

(10)

Shannon小波熵值的大小反映了概率分布的均勻性，最不確定的概率分布(等概率分布)具有最大的熵值。

在突變信號的檢測中，為了突出特征成分,可根據信號特征，自適應地選擇最優帶寬參數fb以使Morlet基小波與特征成分具有最大的相似性。當Shannon小波熵最小時，對應的Morlet基小波就是與特征成分最相似的小波。根據這一原理，可自適應設計出最優Morlet小波。

以仿真信號為例驗證基于Shannon小波熵自適應設計最優Morlet小波的有效性。設信號x(t)為

(11)

以1 Hz的頻率對x(t)采樣1024點，其時域波形如圖1所示。fb的取值范圍為[1,100]，步長為0.5，經計算可得到fb與Shannon小波熵之間的關系如圖2所示。由圖2知，fb=15時，具有最小的小波熵，對應的基小波就是與特征成分最匹配的Morlet小波，其小波變換時頻圖如圖3(b)所示。作為對比，分別令fb取5和95，再作Morlet連續小波變換，時頻圖分別如圖3(a)和3(c)所示。

從圖3可知，當fb取5時，信號的時間分辨率稍好于fb取15時的分辨率，但其頻率分辨率比fb取15時的低，信號的高頻分量與低頻分量沒有分開。當fb取95時，信號的頻率分辨率稍好于fb取15時的分辨率，但其時間分辨率比fb取15時的低，以致信號的兩個高頻分量沒有被分開。fb取15時，信號的時頻聚集性最好，3個分量被清晰的區分開來。綜合考慮時頻分辨率，fb取15時為最優，因此，基于Shannon小波熵自適應設計最優Morlet小波的方法是有效可行的。

圖1 仿真信號時域波形Fig.1 Waveform of the simulated signal

圖2 fb與Shannon小波熵之間的關系曲線Fig.2 Relation curve between fb and Shannon wavelet entropy

圖3 fb取不同值時的Morlet小波變換時頻圖Fig.3 CWT of the simulated signal for various fb

3 基于峭熵比的最佳尺度求取方法

尺度為a的Morlet小波φa(t)的中心頻率為fc/a。在對信號作小波變換時，尺度a控制濾波的頻帶范圍，且濾波效果主要由帶寬參數fb和尺度a決定。因此，設計出最優Morlet小波后，還須求取最佳尺度a，以將含有被調制信號信息最豐富的那個頻段從強噪聲背景信號中分離出來。

譜峭度(spectral kurtosis:SK)本質為每根譜線處的峭度值，其計算公式為[10]

(12)

式(12)中：符號|?|和〈?〉分別表示取模值和數學期望，H(t,f)為被分析振動信號的時頻復包絡。譜峭度較全局指標峭度具有更強的抗噪能力，能從強噪聲信號中檢測到沖擊及其變化的特征，而且還能指出它們出現的頻帶。

由前述，Shannon小波熵值的大小反映了小波系數分布的均勻性。故障沖擊越強的頻帶，其信號幅值分布越不均勻，其譜峭度也越大，Shannon小波熵值越小，故Shannon小波熵值同譜峭度一樣，也能反映信號中的沖擊及其所在的頻帶。但實際信號分析表明，譜峭度的最大值與Shannon小波熵的最小值不一定在同一頻帶取到，也就是說基于譜峭度求取的最佳尺度與基于小波熵求取的最佳尺度不一定是同一尺度。鑒于此，綜合考慮譜峭度與Shannon小波熵，提出一個新的沖擊性評價指標——峭熵比，即譜峭度與Shannon小波熵的比值來衡量各個頻帶的沖擊性。顯然，沖擊性越強的頻帶，其譜峭度越大，且Shannon小波熵值越小，因此其峭熵比也就越大。為此，提出基于峭熵比的最佳尺度的求取方法，其步驟如下：1)對信號進行最優Morlet小波變換；2)用小波系數代替式(12)中的H(t,f)，計算各個尺度的譜峭度；3)將各個尺度的小波系數的實部處理成一個概率分布序列并計算其Shannon小波熵，第j個尺度的Shannon小波熵計算公式為

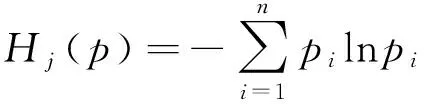
(13)

4 最優Morlet小波自適應包絡解調的弱故障特征提取方法

為了準確提取強噪聲背景下的微弱故障特征，在前文研究基礎上提出基于最優Morlet小波自適應包絡解調的弱故障特征提取方法。該方法首先根據信號的特征成分采用Shannon小波熵方法優化帶寬參數，自適應地設計出最優Morlet小波，并對信號進行最優Morlet連續小波變換。然后，依據峭熵比自適應地求取最佳尺度并提取最佳尺度的小波系數，從而實現對信號的最優帶通濾波。最后，對最佳尺度的小波系數取模即可實現對最優頻帶的包絡解調，提取到最優頻帶的包絡，可得到包絡譜，進而提取到明顯的微弱故障特征。

5 應用實例

實驗數據源自異步電動機滾動軸承故障模擬實驗臺。軸承型號為6205-2RS，滾珠數目Z=9,滾珠直徑dBD=7.94 mm,節徑dPD=39.04 mm,接觸角α=0°。實驗時，軸的轉頻為29 Hz。依據上述參數計算出軸承外、內圈故障特征頻率分別為103 Hz,155 Hz。實驗通過電火花加工方式對軸承外、內圈制造點蝕損傷，模擬軸承早期損傷故障，其中外圈故障的位置與軸承的承載區域相對。

以采樣率fs=12 kHz對軸承外、內圈故障振動信號采樣4096點，采樣信號及其頻譜如圖4(a)和4(b)所示。從圖可知強背景噪聲基本掩蓋了故障沖擊信號以致很難看出原信號存在周期性的故障。

圖4 故障信號及其頻譜Fig.4 Fault signal and its spectral

采用前述方法提取在強背景噪聲下的故障沖擊特征。首先依據最小Shannon小波熵原理優化帶寬參數設計最優Morlet小波。設母小波中心頻率fc取為0.5，fb∈[1,100]，步長為0.5，經計算，可得到各個fb與外、內圈故障信號小波系數的Shannon小波熵之間的關系如圖5所示。

圖5 fb與故障信號小波系數小波熵的關系Fig.5 Relation between fb and fault signal

由圖5(a)可知，fb=33時，外圈故障信號小波系數具有最小的小波熵，其對應的基小波就是與外圈故障信號沖擊最為匹配的Morlet小波。由圖5(b)知，fb=35時，內圈故障信號小波系數的小波熵最小，其對應的基小波就是與內圈故障信號沖擊最為匹配的Morlet小波。得到最優Morlet小波后，可求取最佳尺度。當fb=33時，外圈故障信號的峭熵比與尺度的關系如圖6(a)所示。

圖6 峭熵比與尺度的關系Fig.6 Relation between KER and scale

由圖6(a)可知，外圈故障信號各尺度的峭熵比在頻帶中心頻率為3540Hz的尺度取得最大值，故外圈故障信號小波系數最佳尺度為fs·fc/3540=1.694 9。由圖6(b)可知，內圈故障信號各尺度的峭熵比在頻帶中心頻率為3 420 Hz的尺度取得最大值，即內圈故障信號小波系數最佳尺度為fs·fc/3420=1.725。求得最佳的帶寬參數和變換尺度后，再對故障振動信號進行最優Morlet小波變換并提取最佳尺度的小波系數。外圈故障信號尺度為1.6949的小波系數實部及其頻譜如圖7(a)所示。

圖7 外圈故障信號最優頻帶及其包絡分析Fig.7 Optimal subband of outer race fault signal and its envelope analysis

由于外圈故障的部位在軸承承載區域相對的位置上，因此每一個滾動體經過故障部位時不一定都產生一次明顯沖擊，有可能是兩個或者多個滾動體經過故障部位時才產生一次明顯沖擊，所以外圈故障信號的沖擊間隔可以為外圈故障特征頻率103 Hz倒數的兩倍或多倍，即約為0.01 s的兩倍或多倍，在圖7(a)中間隔為0.01 s,0.02 s,0.03 s的故障沖擊，表明軸承外圈出現故障。為進一步提取外圈故障特征，對最優頻帶小波系數進行包絡解調。即對尺度為1.6949的小波系數取模并求其傅里葉變換，得到小波系數包絡和包絡譜，如圖7(b)所示。從圖中可知，包絡譜在外圈故障特征頻率103 Hz(忽略計算誤差影響)及其二倍頻、三倍頻處有很明顯的譜線，這正是外圈故障的包絡譜特征。因此，最優Morlet小波自適應包絡解調成功的提取到了隱藏在強噪聲背景下的外圈早期故障特征。

同理，可求得內圈故障信號在最佳尺度為1.725的小波系數的實部及其頻譜(如圖8(a)所示)以及相對應的小波系數的包絡和包絡譜(如圖8(b)所示)。由圖8(a)可知，最優Morlet小波同樣清晰地提取淹沒在強噪信號下等間隔沖擊，且每三個連續的沖擊間隔約為0.02 s，即對應內圈故障的特征頻率155 Hz(忽略計算誤差影響)。由圖8(b)中可知，包絡譜在內圈故障特征頻率155 Hz及其二倍頻310 Hz處有很明顯的譜線，這即是內圈故障的包絡譜特征。

圖8 內圈故障信號最優頻帶及其包絡分析Fig.8 Optimal subband of inner race fault signal and its envelope analysis

上述電機軸承故障診斷實例表明，最優Morlet小波自適應包絡解調的弱故障提取方法能有效的提取淹沒在強噪聲背景下的微弱故障特征，可以廣泛的應用于機電設備的早期故障診斷。

6 結 論

1)根據信號自身的沖擊特征，采用基于Shannon小波熵的方法優化帶寬參數設計了最優Morlet小波，自適應地實現其與沖擊特征成分的最優匹配。

2)利用譜峭度與小波熵均能敏感反映沖擊性的特性，提出基于峭熵比的新方法求取最佳變換尺度。該方法綜合考慮了譜峭度與小波熵兩種指標，能有效的求出最佳變換尺度。

3)提出基于最優Morlet小波自適應包絡解調的弱故障特征提取方法。電機軸承故障診斷實例分析表明：該方法無須人工設定濾波中心頻率與帶寬，能自動有效地從強噪背景中提取微弱故障特征。

[1] MING Y，CHEN J，DONG G M．Weakfault feature extraction of rolling bearing based on cyclic Wiener filter envelope spectrum[J]．Mechanical Systems and Signal Process，2011，25(5)：1773-1775．

[2] 安國慶,秦程,郭立煒,等．峭度濾波器用于電機軸承早期故障特征提取[J].電機與控制學報,2014,18(6):55-60.

AN Guoqing,QIN Cheng,GUO Liwei,et al.Kurtosis filter in feature extraction for incipient motor bearing fault diagnosis[J].Electric Machines and Control,2014,18(6):55-60.

[3] 蘇文勝，王奉濤，張志新，等．EMD降噪和譜峭度法在滾動軸承早期故障診斷中的應用[J]．振動與沖擊，2010，3(29)：18-21．

SU W S，WANG F T，ZHANG Z X，et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]．Journal of Vibration and Shock，2010，3(29)：18-21．

[4] YUHTAY S．On the study of applying morlet wavelet to the Hilbert transform for the envelope detection of bearing vibrations[J]．Mechanical Systems and Signal Processing，2009，23(5)：1518-1527．

[5] 程發斌，湯寶平，鐘佑明．基于最優Morlet小波和SVD的濾波消噪方法及故障診斷的應用[J]．振動與沖擊，2008，27(2) ：91-94．

CHEN F B，TANG B P，ZHONG Y M．A denoising method based on optimal Morlet wavelet and singular valuedecomposition and its application in fault diagnosis[J].Journal of Vibration and Shock,2008,27(2): 91-94．

[6] JIN L，LIANGSHENG Q U．Feature extraction based on morlet wavelet and its application for mechanical fault diagnosis[J]．Sound and Vibration，2000，234(1)：135-148．

[7] 何嶺松，李巍華．用Morlet小波進行包絡檢波分析[J]．振動工程學報，2002，15(1):119-122．

HE L S，LI W H．Morlet Wavelet and its application in enveloping[J]．Journal of Vibration Engineering，2002，15(1):119-122．

[8] 蔣永華，湯寶平，董紹江．自適應Morlet小波降噪方法及在軸承故障特征提取中的應用[J]．儀器儀表學報，2010，31(12)：2712-2717．

JIANG Y H，TANG B P，DONG SH J.Denoising method based on adaptive Morlet wavelet and its application in rolling bearing fault feature extraction[J]. Chinese Journal of Scientific Instrument，2010，31(12)：2712-2717．

[9] NIKOLAOU N G，ATONIADIS I A．Demodulation of vibration signals generated by defects in rolling element bearings using complex shifted morlet wavelets[J]．Mechanical Systems and Signal Processing，2002，16(4)：677-694.

[10] SAWALHI N，RANDALL R B，ENDO H．The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis[J]．Mechanical Systems and Signal Processing，2007，21(6)：2616-2633．

(編輯：賈志超)

Method to extract weak fault feature based on optimal Morlet wavelet adaptive envelope demodulation

HOU Xin-guo， NIU Chao， YANG Zhong-lin

(College of Electrical Engineering,Naval University of Engineering,Wuhan 430033)

In order to achieve adaptive optimal match with the impact component,Shannon wavelet entropy is used to optimize bandwidth parameter of the Morlet wavelet to design the optimal Morlet wavelet. Aimed at obtaining the optimal scale,the approach based on kurtosis entropy ratio to acquire the optimal scale is presented. In addition,the method of extracting weak fault feature based on optimal Morlet wavelet adaptive envelope demodulation is proposed.This method performed optimal transform of continuous Morlet wavelet for signal first,and then adaptively obtained optimal scale and extracted wavelet coefficient of the optimal scale based on kurtosis entropy ratio.Finally,by conducting modulo operation for wavelet coefficient of the optimal scale,envelope demodulation of the optimal frequency band was realized and envelope spectrum was obtained,so that the extracting of the weak fault feature was realized. The simulation results and analysis show that the method overcomes the defect that the parameters of band-pass filter are selected by experience of the user in conventional envelope demodulation,and effectively extract the weak fault feature.

optimal morlet wavelet; adaptive envelope demodulation; shannon wavelet entropy; fault feature；kurtosis entropy ratio

2015-10-13

國家自然科學基金(51307178)

侯新國(1972—)，男，博士，副教授，研究方向為信號檢測與處理，電力系統及設備的故障診斷;

牛 超(1983—)，男，碩士研究生，研究方向為信號檢測與處理、機電設備的故障診斷；

侯新國

10.15938/j.emc.2016.10.012

TH 113.1

A

1007-449X(2016)10-0088-06

楊忠林(1978—)，男，碩士，講師，研究方向為信號檢測與處理、電力系統監控與安全管理。