有效建構模型　凸顯數學知識的本質——基于“小數意義”教學的一點思考

江蘇省南通市如東縣掘港鎮環鎮小學　李雪梅

有效建構模型凸顯數學知識的本質——基于“小數意義”教學的一點思考

江蘇省南通市如東縣掘港鎮環鎮小學李雪梅

數學從內在的知識本身的特點來看，具有高度抽象和概括的特征。這一特征決定了數學的發展是一個知識的框架的構建過程。任何一個最簡單的數學問題和數學對象，都是通過人類抽象思維，最后概括的結果。數學從開始的原始的概念，通過幾個原始的概念再一次深化為抽象的另一個更具抽象的概念，數學的概念和邏輯關系，就是通過這樣的不斷地抽象和概括，就建立了數學的知識框架和網絡。每一個人在學習數學的時候，主要是看對數學的理解是否知道知識內在的聯系和抽象的關系，能否形成自己的知識框架，自己建立的知識框架是否科學和合理。對每一個學習數學的人來說，這是決定能否學好數學的關鍵。

教學小數的意義，典型的教法莫過于，讓學生通過對生活實例的觀察、比較以及操作等各種活動，然后抽象概括，得出“十分之幾寫成一位小數，百分之幾寫成兩位小數，千分之幾寫成三位小數……”的結論。好多教師認為這樣的教學是圓滿的，但實際上學生對知識的認識是膚淺的，沒有深度和厚度。這樣的教學只關注了生活意義，沒有知識的框架和知識間的網絡，只有生活經驗喚醒，沒有理性總結；活動味過度，只有活動操作，沒有回顧、思索、提煉。學生通過實例觀察比較和畫圖操作等這些方式得出結論，都無可厚非，但這只是一種合情的歸納推理，沒有深入問題的本質，“小數”的模型并沒有真正在學生的腦子里建立起來。由于這一基本概念沒有打牢，在后面的教學中學生出現各種理解上的錯誤也就可想而知了。只有深入知識的本質和來源，才能有效建立起數學模型。

究其原因，是教師對小數的意義缺乏最本真的理解，沒有從數學的視界考慮教學問題。讓我們先來看看小數的本質意義是什么。上網百度一下，我們就會知道：小數本質上是一種特殊的分數，即十進制分數。十進制分數是根據十進制的位值原則，把十進分數仿照整數的寫法寫成不帶分母的形式，即分母是10n的（n為自然數）分數叫作“十進制分數”。任何一個“十進制分數”都能寫成小數的形式，如7/10=0.7，7/100=0.07，等等。剖析它的本質意義，我們會發現這樣一種知識框架：十進制分數和小數有著密切的聯系，它們意義相同，只是形式不同，“意義”和“形式”是我們教學小數意義的關鍵詞，所以在教學中我們不僅要讓學生明白小數的意義，還要讓學生理解怎樣實現一種形式到另一種形式的轉換。基于這樣的認識，我們的教學就有了明確的目標：第一，使學生借助直觀認識小數的意義，能理解小數和分數的聯系，能根據分數寫出相應的小數；第二，使學生在認識小數意義的過程中，體會數學知識之間的聯系和數的擴展，培養觀察比較、綜合歸納和抽象概括等思維能力，進一步發展數感；第三，使學生主動思考，體會數的不同表示方式，產生對數的表達方式的興趣。我們的教學思路就變得清晰而簡單了，教師也很容易把握教學的重點和難點。因此典型的教法可以做以下的改進：

首先，通過生活實例讓學生充分體會十進制分數的實際意義。例如，1厘米是1米的1/100，是1/100米；4厘米是1米的4/100，是4/100米；12厘米是1米的12/100，是12/100米。然后告訴學生：這樣的分數還可以寫成小數的形式：1/100米=0.01米；4/100米=0.04米；12/100米=0.12米。引導：這里都是幾位小數？（兩位）怎樣的分數可以寫成兩位小數？（百分之幾寫成兩位小數）

接著，還要讓學生理解我們是怎樣把百分之幾轉換成兩位小數的，這是小數最本質的特征之一，也是很多教師在教學中疏忽的地方，這一部分教學可以這樣板書：

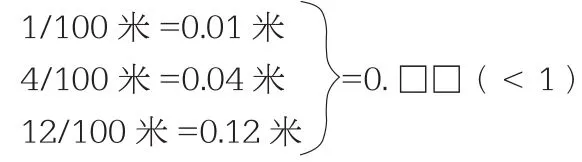
根據以上板書進行引導：在不滿整數“1”的情況下，你有沒有發現小數部分的數就是原來分數的什么？（分子）在不滿整數“1”的情況下，分子最少是一位數，最多是兩位數，所以百分之幾寫成兩位小數。當分子是一位數的時候，把分子寫在小數部分的第二位上，小數部分第一位添0占位；分子是兩位數的時候，就把分子直接寫在小數部分。

同理，（）=0.□□□（在不滿整數“1”的情況下），分子最少是一位數，最多是三位數，所以千分之幾寫成三位小數。分子是一位數的時候，把分子寫在小數部分第三位上，小數部分第一、二位都寫0，分子是兩位數的時候，就把分子寫在小數部分的第二、三位，第一位寫0，分子是三位數的時候，就把分子直接寫在小數部分。通過這樣的教學讓學生體會小數是一種特殊的分數（即分子是10、100、1000……的分數），這種分數和小數只是形式不同而已，其實本質上是一致的，這一點特別重要。這樣學生才能真正建立起“小數”的模型。對于一個學生來說，當一個學生明白了數學知識的本質，才能夠通過學習建立合理的知識框架、合理的知識脈絡。在學生每學完一階段知識的時候，學生才能夠自覺地梳理知識，構建知識框架。

這個例子都告訴我們，小學數學教學常常借用一些日常生活經驗來表征數學概念，這無可厚非。如果僅僅習慣性地、直白地從生活意義去解讀這些概念，所教數學概念的內涵就不那么深刻，就會發生偏差。這樣，學生對數學概念掌握不牢靠也就成了必然的事情。而如果教師能有意識地讓這些生活經驗回歸數學科學的本體，考究這些生活實例的數學意義，并適當利用這些實例的生活意義，那么設計的教學就完全有可能達到一種完美：既充分利用了學生的生活經驗，又超越了經驗層面，提升為初步理性的認識。

數學教學既需要上位的教育學、心理學一般教育理論的指導，更應該尋求以數學視野為基點的各種理性認識的指導。要提升課堂的教學效果和效率，需要教師對數學概念的精準理解，對數學思想方法的把握，對數學思維方式的運用。我們的數學教學就是要具體中見理性，淺顯中見深刻，直白中見經典，這樣才能凸顯知識的本質，有效建構模型，彰顯數學的魅力。